拉格朗日乘子法求二元函數(shù)的最值的慣性誤區(qū)與正確解析

方 侃

（福州大學(xué)至誠學(xué)院，福建 福州 350001）

一、二元函數(shù)求最值的錯解呈現(xiàn)

二元函數(shù)z=f（x，y）在定義域上求最值的問題，許多教材都沒有給出完整的解決方法，［1］吳傳生主編高等教育出版社出版的經(jīng)濟數(shù)學(xué)—微積分下冊有談到二元函數(shù)的最大值與最小值的內(nèi)容，其中提到：“如果f（x，y）在有界閉區(qū)域D上連續(xù)，則f（x，y）在此有界閉區(qū)域上一定能取到最大值和最小值。而使得函數(shù)取到最大值或最小值的點既有可能在此有界閉區(qū)域的內(nèi)部，也可能在此有界閉區(qū)域的邊界上。如果我們假設(shè)，f（x，y）在D上連續(xù)，在D內(nèi)可微且只有有限個駐點，這時候函數(shù)f（x，y）在D的內(nèi)部取得的最大值（最小值）也就是函數(shù)的極大值（極小值）。那么，在上述假設(shè)下，求函數(shù)的最值的過程是：求出函數(shù)f（x，y）在D內(nèi)的所有駐點，然后將對應(yīng)的函數(shù)值與函數(shù)在D的邊界上的最值進行比較，其中最大（小）的就是最大（小）值。但是這種方法，需要求得函數(shù)在D的邊界上的最大值和最小值，此過程通常非常復(fù)雜。因而在實際問題中，如果函數(shù)在D內(nèi)只有唯一駐點，則該駐點處的函數(shù)值就是函數(shù)f（x，y）在D上的最大值（最小值）。教材中舉的例子也是有唯一駐點的實際例題，用拉格朗日乘子法求出唯一極值點后就是最值點。

二元函數(shù)的最值求解是一個難題，筆者在教學(xué)中，發(fā)現(xiàn)解二元函數(shù)最值的一個普遍性錯誤，以下我們就探討［2］同濟大學(xué)數(shù)學(xué)系主編高等教育出版社出版的《微積分》下冊的教材關(guān)于有界閉集D上連續(xù)可微的二元函數(shù)求最值用拉格朗日乘子法計算時的錯誤解法。

同濟大學(xué)數(shù)學(xué)系編的微積分下冊P111頁談到：“下面討論如何求二元函數(shù)z=f（x，y）在有界閉區(qū)域上的最值問題。假設(shè)函數(shù)f（x，y）在有界閉區(qū)域D上連續(xù)而且可微，則由連續(xù)函數(shù)的最大值最小值定理可知在D上必存在最大值和最小值。如果最大值或最小值在D的內(nèi)部取得，那么這些最大值點或最小值點必然是駐點。據(jù)此可以先求出f（x，y）在D的內(nèi)部所有駐點的函數(shù)值。然后利用求解條件極值的方法求出f（x，y）在D的邊界上的最大值和最小值。最后，將上面所得到的這些值加以比較，其中最大的就是最大值，最小的就是最小值。”

例題4；求f（x，y）=2x2+y2在閉區(qū)域D={（x，y）|2（x-1）2+（y-1）2≤12}上的最大值和最小值。

解：先用拉格朗日乘子法求出f（x，y）在邊界D={（x，y）|2（x-1）2+（y-1）2=12}上可能的極值點。作 L（x，y，l）=2x2+y2+l［2（x-1）2+（y-1）2-12］，求解方程組：

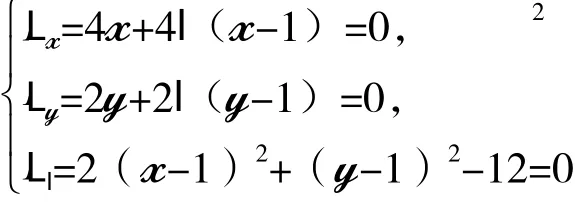
解得f（x，y）在橢圓邊界D={（x，y）|2（x-1）2+（y-1）2=12}上的兩個可能極值點M1（3，3），M2（-1，-1）。

再求f（x，y）在D內(nèi)部{（x，y）|2（x-1）2+（y-1）2＜12}的可能極值點，由于fx=4x，fy=2y，因此由fx=fy=0解得唯一駐點M3（0，0）。

由于f（3，3）=27，f（-1，-1）=3，f（0，0）=0，因此f（x，y）在D上的最大值為27，在D上的邊界點M1取得；最小值為0，在D的內(nèi)點M3取得。

現(xiàn)在按照以上解題思路和過程，解答P113頁3.（3）：f（x，y）=1+xy-x-y，D是由曲線y=x2和直線y=4所圍成的有界閉區(qū)域。

解：先用拉格朗日乘子法求出f（x，y）在邊界D={（x，y）|y=x2}上可能的極值點。作L（x，y，l）=1+xy-x-y+l（y-x2），求解方程組：

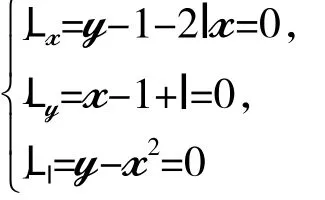
解得f（x，y）在邊界上的兩個可能極值點M1（1，

先用拉格朗日乘子法求出f（x，y）在邊界D={（x，y）|y=4}上可能的極值點。作L（x，y，l）=1+xy-x-y+l（y-4），求解方程組：

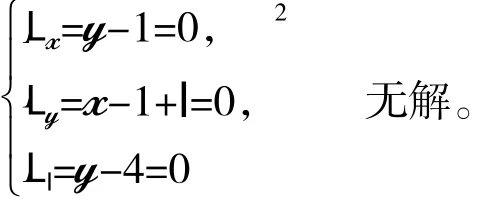
再求f（x，y）在D內(nèi)部{（x，y）|x2＜y＜4}的可能極值點，由于fx=y-1，fy=x-1，因此由fx=fy=0解得唯一駐點M3（1，1）。

這樣算出的答案與習題后的參考答案一致，然而這個答案是錯誤的。因為f（-2，4）=-9，f（2，4）=3，而這兩個點顯然包含在D={（x，y）|x2≤y≤4}這個有界閉區(qū)域上，因此f（-2，4）=-9，f（2，4）=3，就分別是 f（x，y）=1+xy-x-y在D={（x，y）|x2≤y≤4}這個有界閉區(qū)域上的最小值和最大值。

二、二元函數(shù)求最值的錯因分析

我們從一元函數(shù)求最值來分析。一元函數(shù)y=f（x）在閉區(qū)間［a，b］上求最值的過程：先求極值點，再比較端點y=f（a），y=f（b）的值，最后得到最大最小值。因此，二元函數(shù)z=f（x，y）在有界閉區(qū)域Dxy求最值，我們同樣是要先求二元函數(shù)z=f（x，y）在D的內(nèi)部的極值點，再跟邊界值比較，得到最大值最小值。只是二元函數(shù)的邊界要比一元函數(shù)復(fù)雜許多，一元函數(shù)就是兩個端點，二元函數(shù)是由若干條曲線構(gòu)成。在求內(nèi)部極值點的時候，上面例4的過程沒有任何問題，問題出在用拉格朗日乘子法求邊界值的時候，其實仍然解決的是內(nèi)部的極值問題，而不是最值問題，要解決最值，還必須把邊界約束條件代入二元函數(shù)z=f（x，y）化為一元函數(shù)y=f（x）后的x端點值考慮進去比較。

三、二元函數(shù)求最值的正確解法

例4解（一）：的第一部分用拉格朗日乘子法求完，必須再跟兩個x的端點后的二元函數(shù)值比較結(jié)果終比較過，雖然答案不變，但那只是因為極值點恰好是最值點，事實上，［3］顧江永李紅玲的文章中列出四種解法的解法三，用拉格朗日乘子法求邊界點的時候也是忽略了要用端點值來比較的這個細節(jié)問題。此外，例四也可以用參數(shù)代換法化為一元函數(shù)來解題。

例4解（二）：先求f（x，y）在D內(nèi)部{（x，y）|2（x-1）2+（y-1）2＜12}的可能極值點，由于fx=4，fy=2y，因此由fx=fy=0解得唯一駐點M3（0，0）得f（0，0）=0。

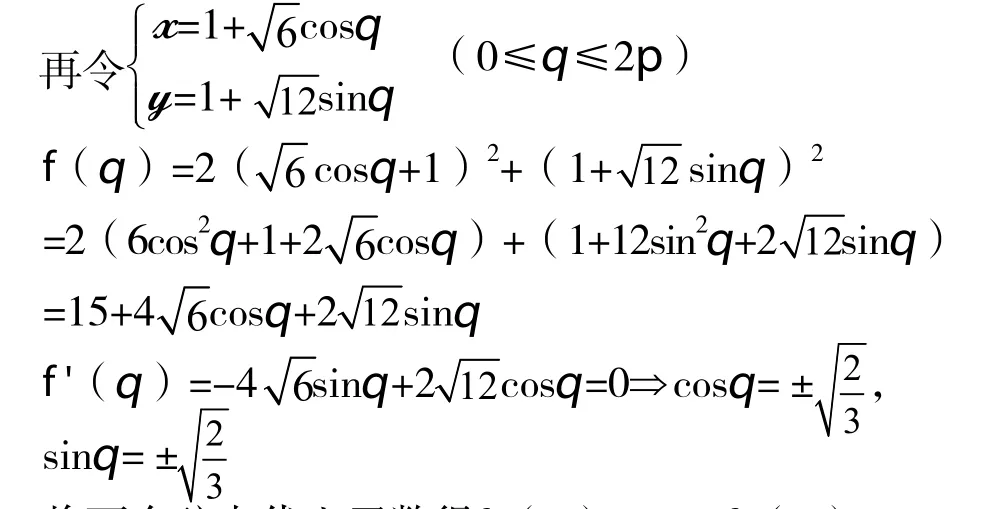
將兩個駐點代入函數(shù)得f1（q）=27，f2（q）=3。

而［2］教材中課后習題3.（3）答案就錯了，正確的解法如下：

法一（拉格朗日乘子法）：

解：內(nèi)部問題：求f（x，y）在D內(nèi)部{（x，y）|x2＜y＜4}的可能極值點，由于fx=y-1，fy=x-1因此由fx=fy=0解得唯一駐點M3（1，1）。

邊界問題：按照上面第一次解答所述的過程用拉格朗日乘子法求出極值點后，再比較端點值f（-2，4）=-9，f（2，4）=3，由此比較得到f（x）的最小值為-9，最大值為3。

法二（化為一元函數(shù)）：

解：內(nèi)部問題：求f（x，y）在D內(nèi)部{（x，y）|x2＜y＜4}的可能極值點，由于fx=y-1，fy=x-1因此由fx=fy=0解得唯一駐點M3（1，1）.

邊界問題；將y=x2（-2≤x≤2）代入f（x，y）得，f（x）=1+x3-x-x2，f ′（x）=3x2-1-2x=0，得駐加上端點x=±2。

將y=4（-2≤x≤2）代入f（x，y）得，f（x）=1+4x-x-4=3x-3，由此比較得到f（x）的最小值為-9，最大值為3。

四、二元函數(shù)求最值的總結(jié)啟示

在閉區(qū)域上連續(xù)可微的二元函數(shù)的最值問題，用拉格朗日乘子法求以邊界曲線為約束的條件極值，得到的僅僅是極值，和將邊界曲線代入二元函數(shù)化為一元函數(shù)求導(dǎo)得到的極值點性質(zhì)是一樣的，都只能解決的是極值。要想得到最值，必須把邊界曲線代入二元函數(shù)化為一元函數(shù)后，一元變量的端點值考慮進去，最后比較得到的才是最大值和最小值。文章糾正了［2］《微積分》下冊第六章關(guān)于用拉格朗日乘子法求在有界閉區(qū)域上連續(xù)可微的函數(shù)的最值過程中的一個慣性思維解題的錯誤。二元函數(shù)求最值的題型通常是困難的，解決此類問題，必須要細心，注重培養(yǎng)思維的嚴謹性。平常教學(xué)中，我們應(yīng)盡量降低難度，重點立足于解決最值的應(yīng)用問題,即唯一駐點就是最值點的實際問題，以便學(xué)生能更好理解此類解法的本質(zhì)。