基于多參數測量的雙向受控隱形傳態

彭家寅

內江師范學院 數學與信息科學學院，四川 內江 641199

1 引言

自Bennett等[1]于1993年率先提出量子隱形傳態以來，諸如量子信息分享[2]、受控隱形傳態[3]、分層量子信息分享[4]、遠程態制備[5]、聯合遠程態制備[6]、量子信息集中[7]等一些隱形傳態修改方案被報道。原始的隱形傳態方案是一個單方發送方案，其中發送者利用兩比特經典信息和一個事先在發送方和接受方分享的糾纏態，把一個未知單粒子態傳送給接收者。此后，Huelga等[8-9]討論了利用雙向隱形傳態去執行非局域量子門的可能性。最近，Zha等[10-11]提出了雙向受控隱形傳態協議，它是一個三方方案，其中控制者起到了在兩個方向通信的控制作用，僅當在控制者的許可下，雙向隱形傳態任務方可完成。上述這些方案幾乎都是確定性的，即實現方案的成功概率是1，且使用的量子糾纏資源都是最大量子糾纏態。然而，在真實環境中，量子系統不可避免地要受到噪聲的干擾，量子糾纏就要退化為非最大糾纏態或混合態。因此，學者們采用非最大糾纏態作為量子資源來執行量子任務，包括量子態分享[12-13]、分層量子信息分裂[14]、量子隱形傳態[15]、量子信息集中[16]、遠程量子態制備[17]等。2015年，Fortes和Rigolin[18]利用單參數測量研究了噪聲隱形傳態的效率問題，其自由參數的選擇有助于優化隱形傳態的效率。2018年，Wei等[19]提出了以非最大糾纏態為信道的多參數測量的隱形傳態方案，指出了該方案成功的概率與測量參數和量子信道的糾纏因子成正相關，而與經典耗費成負相關。本文考慮到含參數測量有趣特征與現實環境中噪聲的影響，討論以五粒子非最大糾纏團簇態為量子信道，基于多參數測量的雙向受控隱形傳態問題，并分析其成功概率、資源耗費及相關參數間的關系。

2 量子任務和團簇態

當然，這個任務可以通過兩個概率受控隱形傳態協議來笨拙地完成，每個協議需耗費一個三粒子Greenberger-Horne-Zeilinger態作為量子信道及一個控制者，總共涉及6比特非局域量子資源和兩個獨立的控制者。本文的目標是設計一個協議，使得Alice和Bob同時、確定性地交換他們所擁有的量子態，并且只能使用唯一一個5比特非局域資源，以及唯一一個共有的控制者。

在本文方案中使用了一個5比特非最大糾纏態作為量子信道，它源于一個多粒子糾纏團簇態，這類原始態是由Briegel等[20]為實現基于測量而不是基于常規酉運算線路的量子計算的新范式而引入的。此后，通過不同物理系統生成這類量子態的各種方案被報道[21-24]。N-比特線性團簇態可以表示為：

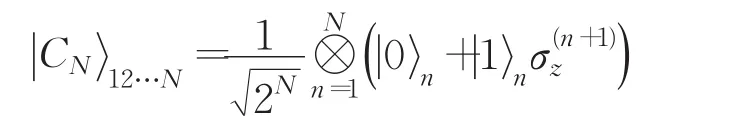
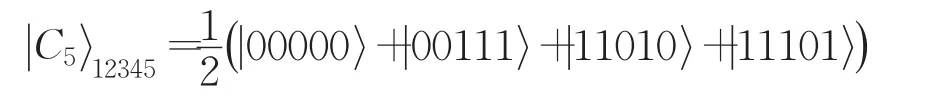
將它改寫成：

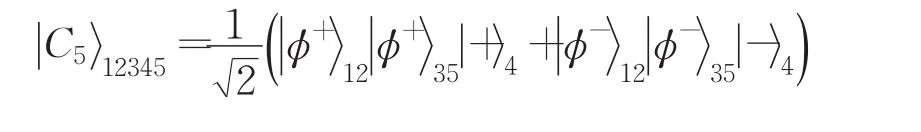
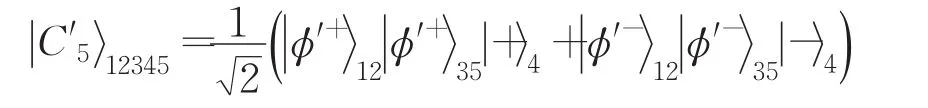
其中

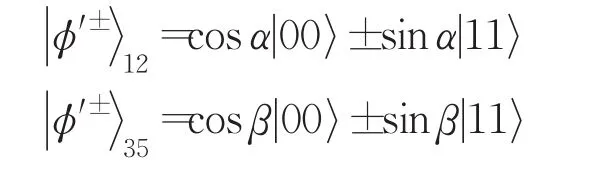
且 α,β∈(0,π/4]，作為量子信道，這里粒子1、3屬于Alice，粒子2、5屬于Bob，而粒子4屬于Charlie。該信道是一個非最大糾纏信道。顯然，當α=β=π/4時，即被Alice、Bob和Charlie事先分享的量子信道是一個標準5比特團簇態，也是一個最大糾纏態。

由粒子 A、B、1、2、3、4和5構成的復合系統為：

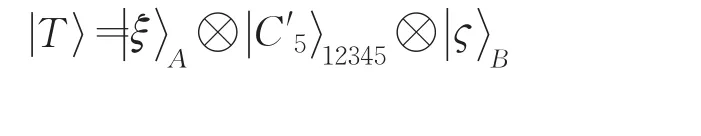
3 雙向受控隱形傳態協議

為了實現基于多參數測量的雙向受控隱形傳態，Alice在粒子A和1進行兩粒子測量，測量基如下：

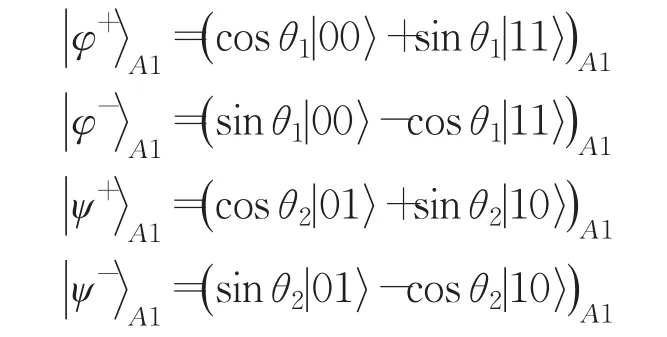
其中，θ1和 θ2是測量參數，且 θ1,θ2∈(0,π/4]，當 θ1=θ2=π/4時，該測量基就是Bell基。同時，Bob對粒子B和5進行兩粒子測量，測量基為：

其中，τ1和 τ2是測量參數，且 τ1,τ2∈(0,π/4]，當 τ1=τ2=π/4時，該測量基也是Bell基。顯然，上述兩組測量基共含有4個參數。利用這兩組基可將整個系統改寫為：

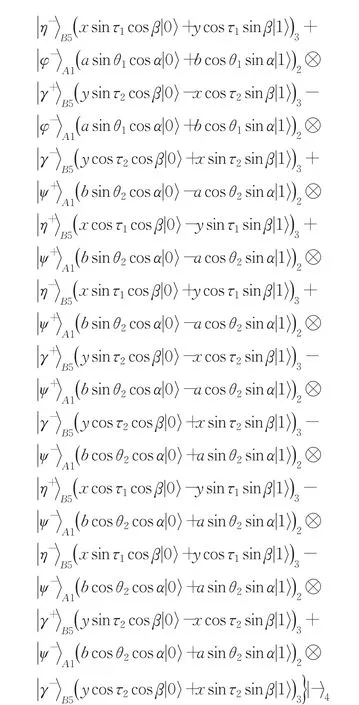
Alice和Bob測量后將結果告知對方與Charlie。Charlie用基對粒子4進行測量，并公布其測量結果，執行測量后，整個態塌陷為32種類型之一。例如，Alice測量結果為，Bob的測量結果為Charlie的測量結果為時，余下粒子2和3的態塌陷為：

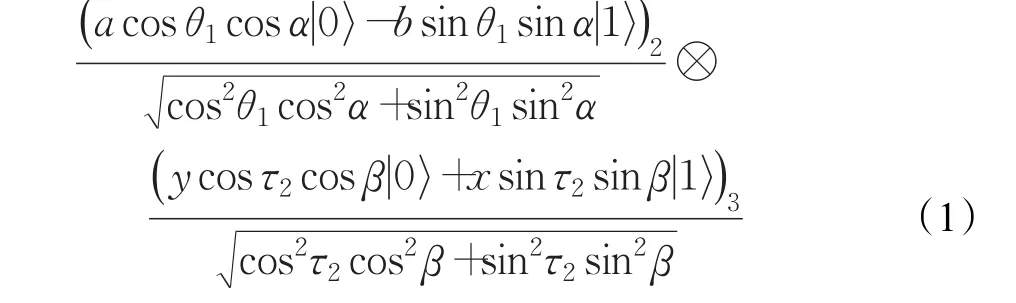
根據收到的測量結果，Alice和Bob需要做如下一些相應的操作：他們應分別引入初始態為的輔助粒子A′和B′，結合收到的測量結果分別對粒子對(3,A′)與(2,B′)執行U(u,v)操作（它的選取依賴測量結果），它的具體形式如下：

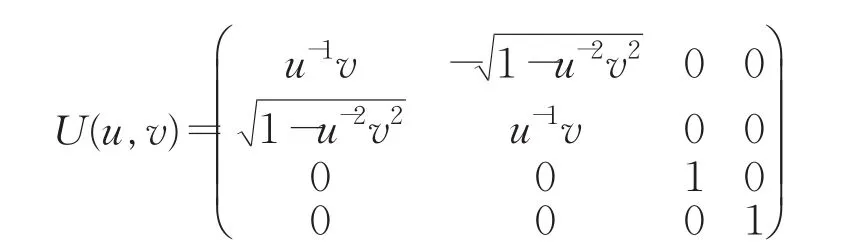
例如對應于式（1）的情況，Alice引入輔助粒子A′，Bob引入輔助粒子B′后系統變成：

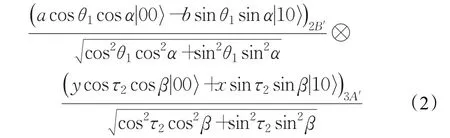
注意到 α,β,θ1,τ2∈(0,π/4]有：

因此 Alice的 U(cosτ2cosβ,sinτ2sinβ)與 Bob 的U(cosθ1cosα,sinθ1sinα)都應取上述兩個矩陣形式中的第一種矩陣。他們施行酉變換后，式（2）變成：

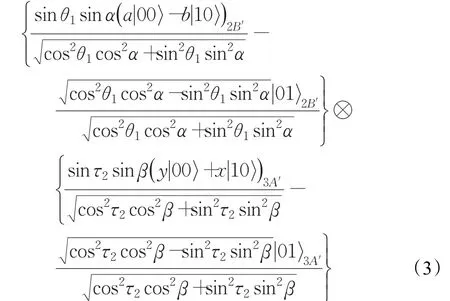
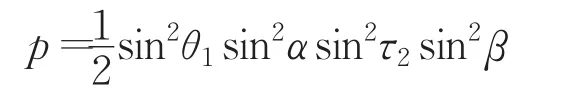
測量后，式（3）變成：

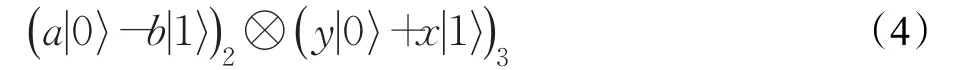
為了重構原始秘密態，Alice需要對粒子3實施ZPauli門操作，而Bob則需要對粒子2執行X-Pauli門操作，從而式（4）變成：

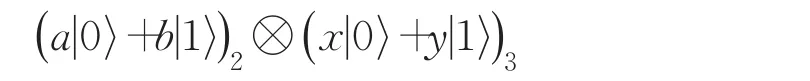
接下來計算上述協議成功的總概率，以及總的資源耗費情況。

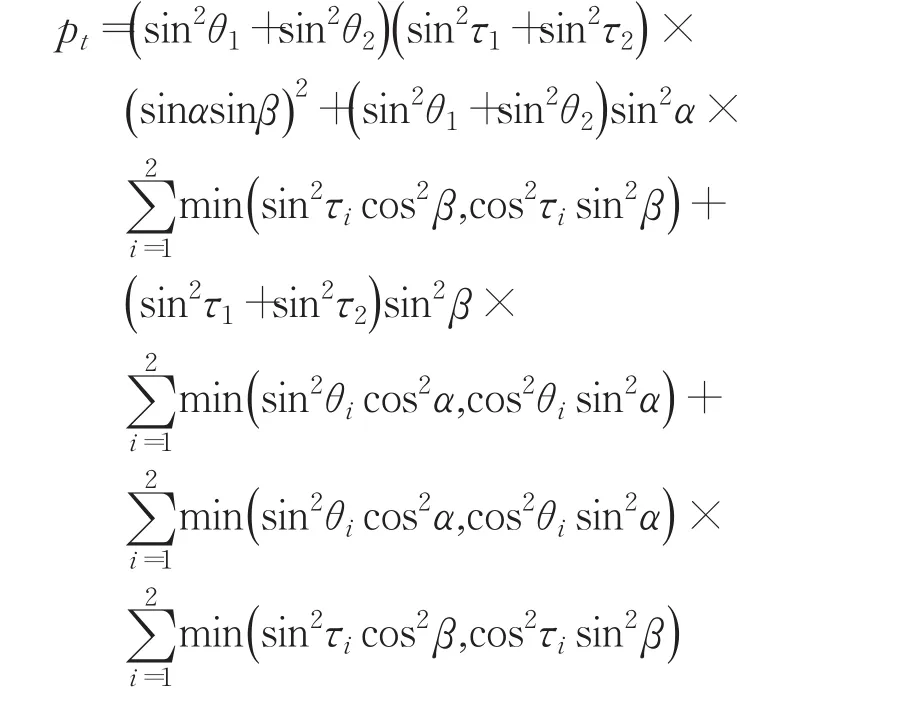
從上式可以看出，本方案成功的概率 pt與量子信道的糾纏參數 α、β 和測量基的參數 θ1、θ2、τ1及 τ2有關。當 α=β=θ1=θ2=τ1=τ2=π/4時，得到最大的成功概率 pt=1，此時，量子信道最大糾纏的5比特團簇態，兩組測量基都是Bell基，本方案是確定性的。

利用文獻[25-26]給出的經典耗費的計算方法，按改寫系統之表達式的順序對應的塌陷態成功恢復的概率記為 pi，則經典耗費為：

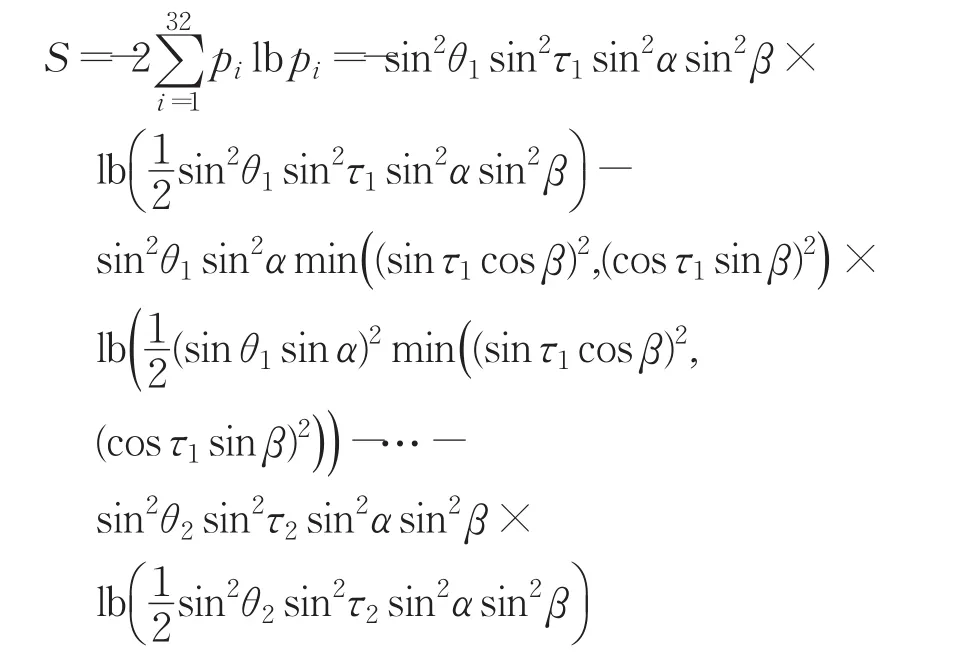
上式表明經典耗費也依賴于量子信道的糾纏參數α、β 和測量基的參數 θ1、θ2、τ1及 τ2。當 α=β=θ1=θ2=τ1=τ2=π/4時，s=10，即量子信道最大糾纏的5比特團簇態，兩組測量基都是Bell基時，經典耗費為10比特。

從上述兩方面的討論中不難發現，本文方案在α=β=θ1=θ2=τ1=τ2=π/4時，就是通常標準的雙向受控隱形傳態方案。

4 結論

本文融合了雙向隱形傳態、受控隱形傳態、概率隱形傳態和多參數測量思想，提出了一個在真實環境中更實用的量子通信協議。該協議選擇了比W態和GHZ態的魯棒性更好的非最大糾纏5粒子團簇態為量子信道，發送者采用多參數的通用測量，接收者需引入輔助粒子，在監控者的許可下，充分利用測量信息來進行適當酉變換，就能以一定的概率同時交換他們的量子信息。由于本方案中的量子糾纏參數和測量參數的可調整性，可以適當地調節方案的成功概率和經典耗費，進而使方案更廣泛使用于現實生活的各種不同需求，對實際應用具有較好的指導意義。值得一提的是，本方案為標準的雙向受控隱形傳態的推廣。