區間Pythagorean模糊交互式多準則決策模型

李 娜，高雷阜，王 磊

1.遼寧工程技術大學 基礎教學部，遼寧 葫蘆島 125105

2.遼寧工程技術大學 理學院，遼寧 阜新 123000

1 引言

多準則決策主要研究在多個準則下選擇最優方案或對有限的方案進行排序和評價，是決策分析理論的重要內容之一，其理論與方法在經濟、管理、工程和軍事等諸多領域都有廣泛的應用[1-4]。由于客觀事物的復雜性和不確定性，現代大型決策往往不僅需要多個決策者參與，而且需要多次反復、不斷地對決策意見進行協調和修正，因此，交互式決策過程顯得十分重要。徐澤水[5]充分利用已知客觀信息的同時又可最大限度地考慮決策者的交互要求下，提出一種交互式多準則決策方法，從而使決策更具合理性。徐澤水[6]提出了一種基于殘缺互補判斷矩陣的交互式群決策方法。陳建中等[7]基于TOPSIS的方法，提出一套可以綜合序數性偏好表示，多輪交互逐步逼近的群決策綜合方法。王玉寶[8]提出一種基于方案集縮減策略的交互式多屬性決策方法。周宏安[9]提出了基于方案貼近度和滿意度的交互式多屬性決策方法。

由于客觀事物的復雜性、不確定性以及人類思維的模糊性，當決策者受一些主、客觀因素制約時，他們往往以不確定語言方式描述評價信息。Xu等[10]研究了準則權重信息部分已知，評價信息由三角模糊數刻畫的交互式決策問題。文獻[11]基于概率權重具有穩定性和結果價值具有模糊性兩項條件，提出了兩層交互式有限理性決策方法。在部分權重信息下的不確定語言環境下，文獻[12]建立了一些決策者與分析者之間不斷交互的線性規劃模型，然后在此基礎上提出了一種實用的交互式選擇最佳方案的方法。在直覺模糊環境下，肖建彪[13]在部分權重信息下，基于方案的期望水平、達成度、滿意度等概念，提出了一種交互式多屬性決策方法。Xu[14]將文獻[10]的模糊環境下的研究結果推廣到直覺模糊環境下。胡浩等[15]通過計算各個專家對方案的偏好矢量與理想方案偏好矢量間的相似度，提出了直覺模糊動態信息下的交互式決策方法。

在實際決策過程中，由于環境的復雜性和人的認知，決策者可能給出一個方案滿足和不滿足一個準則的程度之和大于1的情況。例如：評價軟件開發項目，對于技術可行性這個準則，決策者給出具有這個準則的程度為0.5，而不具有這個準則的程度可能為0.6，由于0.5+0.6＞1，直覺模糊數無法描述，但0.52+0.62=0.61＜1。為此，Yager等[16-17]于2014年提出了Pythagorean模糊集，其特點是隸屬度與非隸屬度之和可以大于1，但隸屬度與非隸屬度的平方和小于等于1，可見Pythagorean模糊集是對直覺模糊集的一種擴展，因此在處理模糊性和不確定性信息方面具有更強的表現能力。目前在Pythagorean模糊環境下，多準則決策已有一些研究[18-21]，但交互式多準則決策問題還未見報道。為此，本文在準則權重信息部分已知的情況下，研究準則值為區間Pythagorean模糊數的交互式多準則決策問題。

2 基本概念

定義1[16]設X為一個給定論域，稱P={＜x,μP(x),vP(x)＞|x∈X}為 X上的Pythagorean模糊集，其中，μP(x)∈[0,1],vP(x)∈[0,1],且表示x對p的隸屬程度，vP(x)表示x對 p的非隸屬程度，為x對 p的猶豫度。

為了表示方便，稱 α=(μα,vα)為 Pythagorean 模糊數[14]，其中，記X上的Pythagorean模糊數為PFN(X)。

定義2[16]設 X 為一個給定論域，稱為 X 上的區間Pythagorean模糊集，其中且,猶豫度區間為：

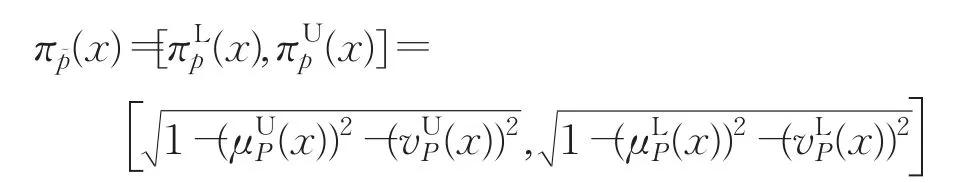
定義3[17]令，稱為區間Pythagorean模糊數?的得分值，其中s為得分函數。顯然越大，越大。

3 區間Pythagorean模糊信息下的交互式多準則決策

3.1 問題描述

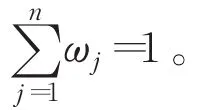
定義4 設為第 i個方案，ω =(ω1,ω2,…,ωn)T為準則權向量，稱

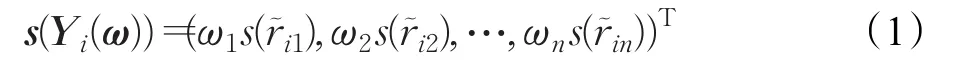
為方案Yi的加權得分向量，且稱

為 s(Yi(ω))的模。

方案Yi,i=1,2,…,m的模s(Yi(ω))越大，表明方案Yi,i=1,2,…,m 越好，若準則權向量 ω=(ω1,ω2,…,ωn)T已知，則通過式（2）得到每個方案的模，進而通過模的大小進行排序。實際決策過程中，往往對準則權向量信息的了解只是部分的，接下來研究準則權重不完全確定情形下的決策。

3.2 準則權重的確定

定義5分別稱

為區間Pythagorean模糊正理想方案和區間Pythagorean模糊負理想方案，其中：

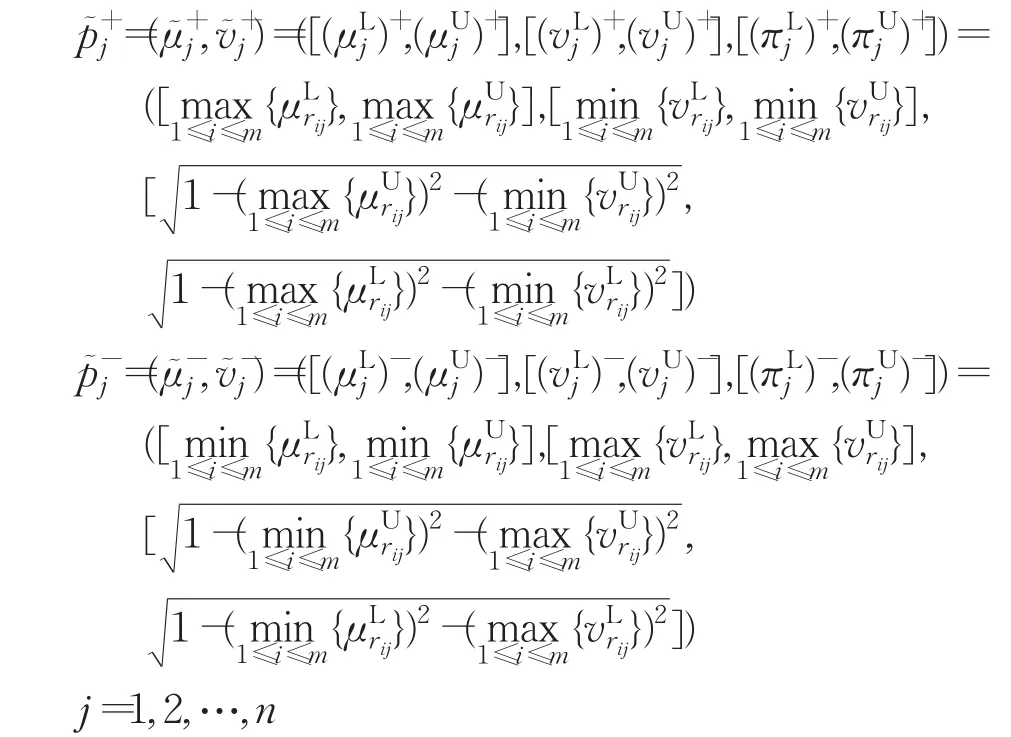
定義6 設為區間 Pythagorean 模糊正理想方案為準則權向量，稱

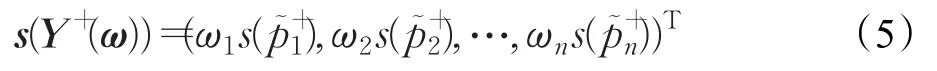
為區間Pythagorean模糊正理想方案Y+的加權得分向量，且稱

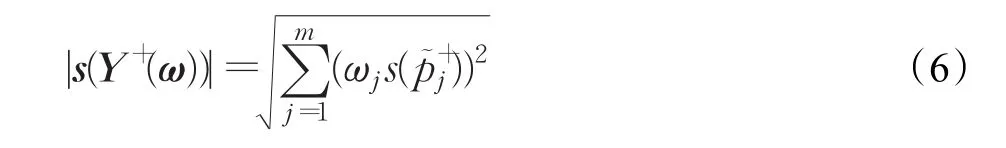
為 s(Y+(ω))的模。

類似定義6有定義7。

定義7 設為區間 Pythagorean 模糊負理想方案，為準則權向量，稱

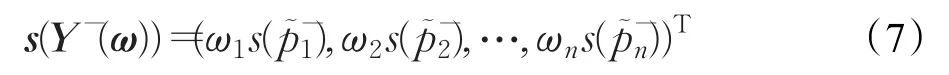
為區間Pythagorean模糊負理想方案Y-的加權得分向量，且稱

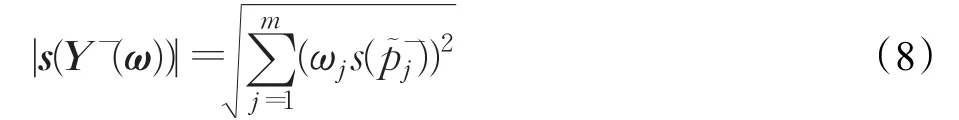
為 s(Y-(ω))的模。

定義8設

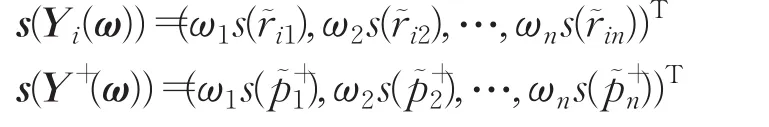
分別為方案Yi和區間Pythagorean模糊正理想方案Y+的加權得分向量，稱

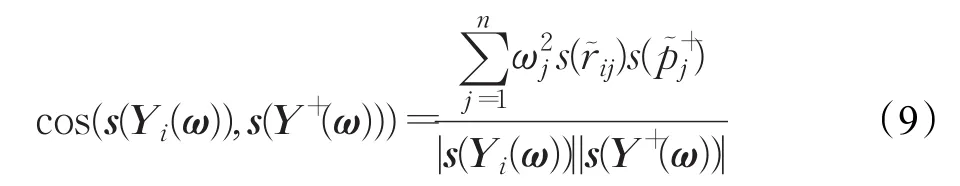
為s(Yi(ω))和s(Y+(ω))的相關系數，即夾角余弦。并稱

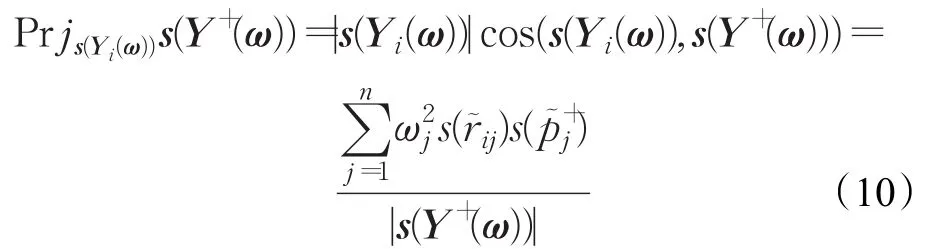
為 s(Yi(ω))在 s(Y+(ω))的投影。的值越大，說明 s(Yi(ω))越接近 s(Y+(ω))，即方案Yi越好。關于相關系數顯然有如下結論。

定理1設

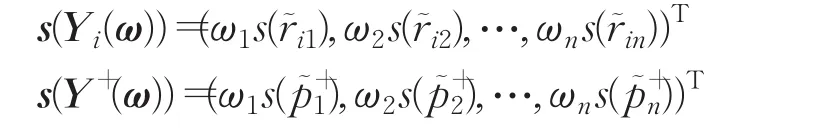
分別為方案Yi和區間Pythagorean模糊正理想方案Y+的加權得分向量，則：

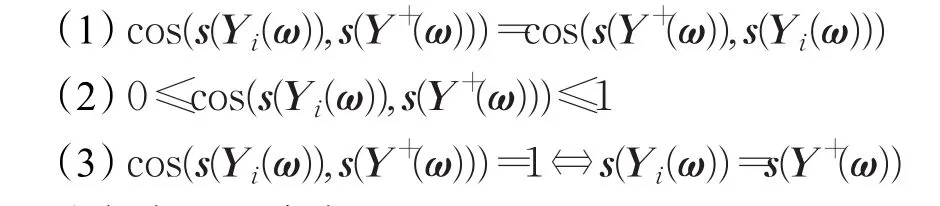
類似定義8，有定義9。

定義9設

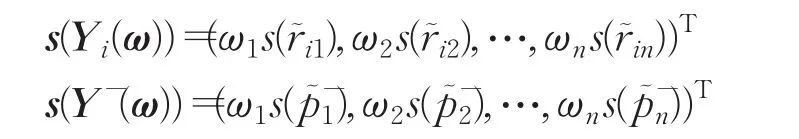
分別為方案Yi和區間Pythagorean模糊負理想方案Y-的加權得分向量，稱

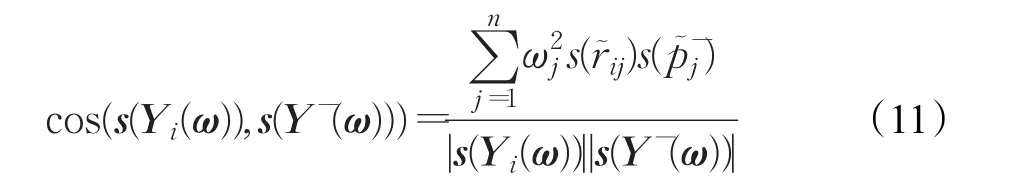
為s(Yi(ω))和s(Y-(ω))的相關系數，即夾角余弦。并稱

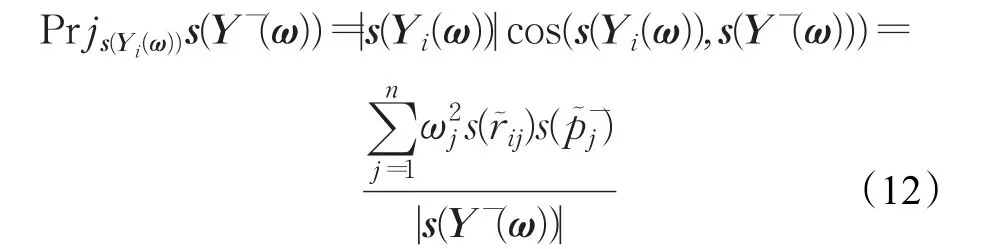
為 s(Yi(ω))在 s(Y-(ω))的投影。

定理2設

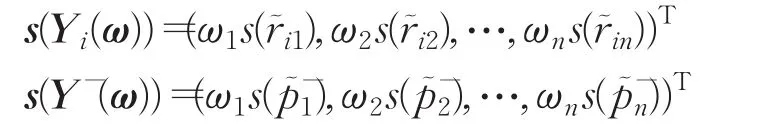
分別為方案Yi和區間Pythagorean模糊負理想方案Y-的加權得分向量，則：

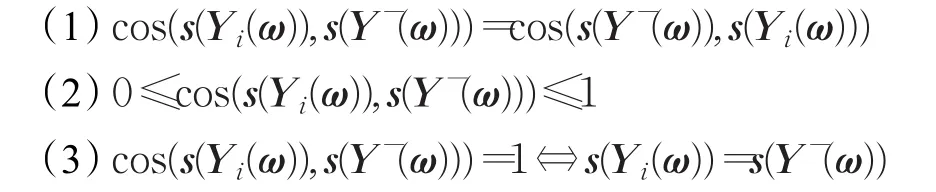
決策過程中，僅僅單獨利用式（10）或（12）評價方案并不全面，為此將式（10）和（12）綜合起來，得到定義10。

定義10稱

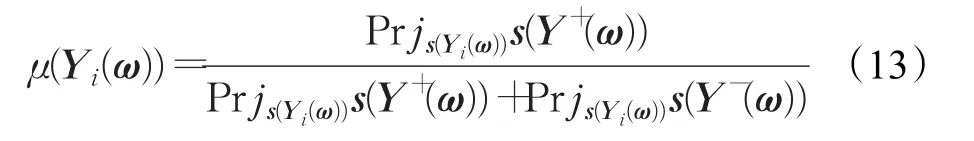
為方案Yi的滿意度。

滿意度μ(Yi(ω))反映了方案Yi總屬性值的大小，μ(Yi(ω))的值越大，說明方案 Yi越好，且 μ(Yi(ω))∈[0,1]。

為了確定權重，建立如下多目標優化模型：

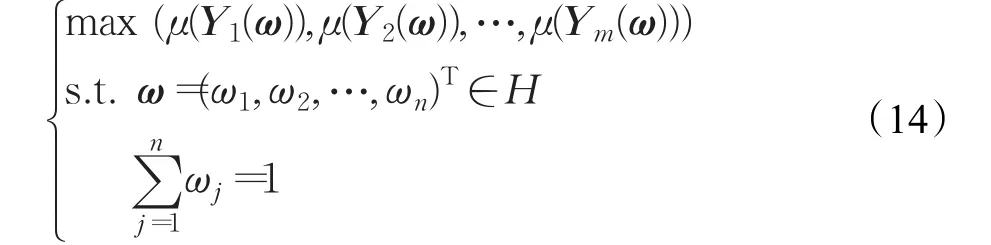
其中，H為屬性權重信息不完全的數學表達式集合。

根據多目標優化理論中的線性加權和法，考慮到各個方案之間的公平競爭，模型（14）可轉化為如下的單目標優化模型：

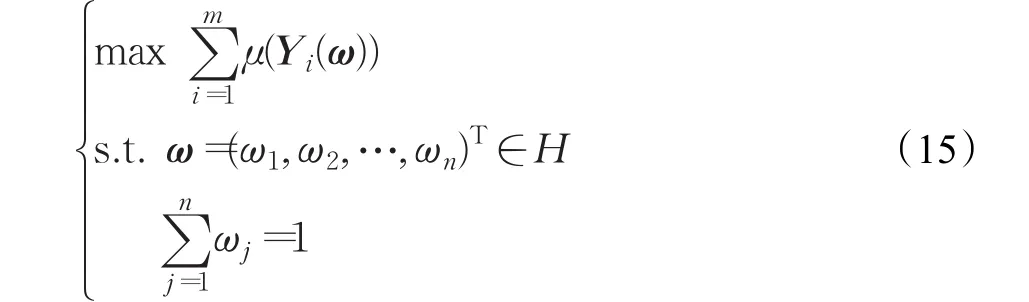
定理3單目標優化模型（15）的最優解為多目標優化模型（14）的有效解。

證明方法同文獻[13]。

3.3 交互式決策步驟

考慮到決策者的偏好，實際決策過程中由模型（14）和模型（15）解出的某些方案的滿意度過大，相比而言另一些方案的滿意度過小，決策者可能要對方案的滿意度進行調整，為此建立如下交互式優化模型：

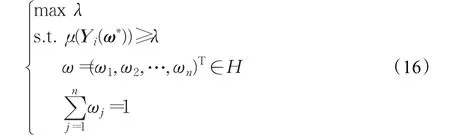
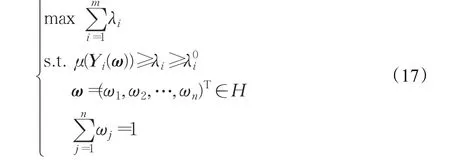
定理4單目標優化模型（17）的最優解是多目標優化模型（14）的有效解。

證明方法同文獻[13]。

基于以上分析，下面給出Pythagorean模糊信息下權重信息不完全確定的區間多準則決策問題的交互式決策方法。

步驟1利用模型（16）求出初始最優權重向量ω(0)=計算每個方案的初始滿意度i=1,2,…,m，決策者據此給出每個方案滿意度的下限值λ(0)i,i=1,2,…,m。令c=1。

步驟2利用模型（17）求出最優權重向量計算每個方案的滿意度2,…,m。

步驟3若決策者對步驟2的所得結果滿意，則利用式（2）計算出的每個方案的模 s(Yi(ω)),i=1,2,…,m,對方案進行排序，并轉步驟4。若模型（17）無解或者決策者對結果不滿意，則決策者根據需要適當提高一些方案的最低滿意度，同時降低另一些方案的最低滿意度，令c=c+1，然后轉步驟2。

步驟4結束。

4 算例分析

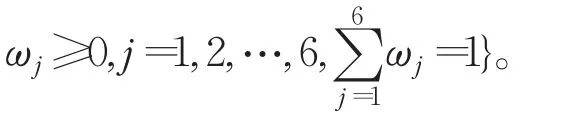
步驟1利用模型（16）建立優化模型（18）。

步驟2利用模型（17）建立優化模型（19）。

利用軟件Matlab7.0求解該模型，無解。表明決策者給出某些方案滿意度的下限值相比初始權向量確定出的滿意度過大，如方案

下面決策者對方案滿意度的下限值進行調整，如下：

表1 區間Pythagorean模糊決策矩陣R

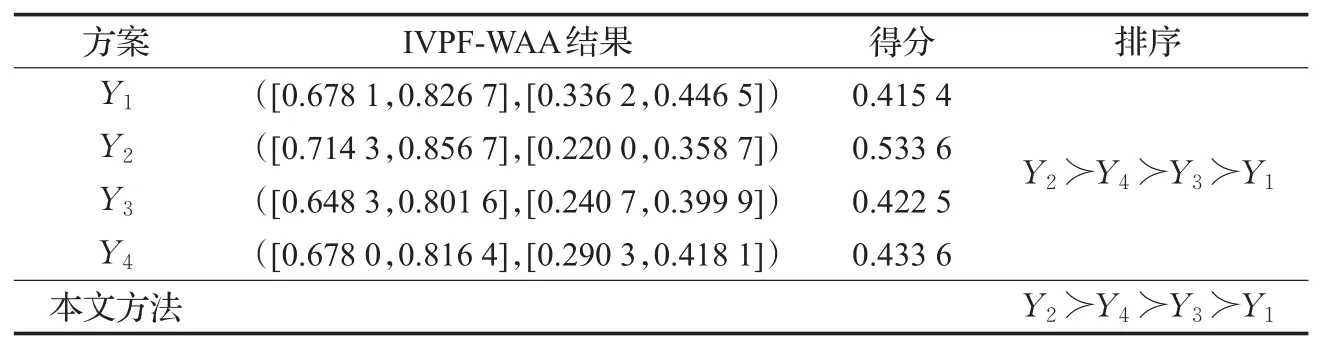
表2 兩種方法結果對比

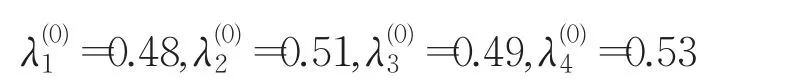
于是重新求解模型（19）得最優準則權重向量為：

由該準則權向量計算每個方案的滿意度為：

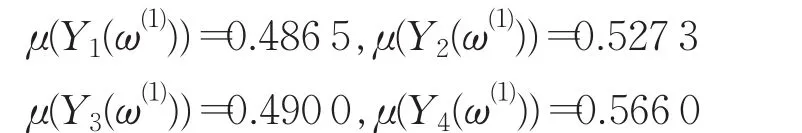
步驟3決策者對此結果感到滿意，利用式（2）算得每個方案的模為：

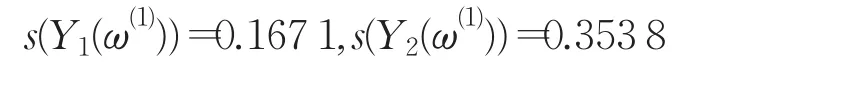
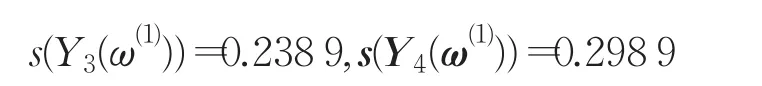
于是得到排序結果為：

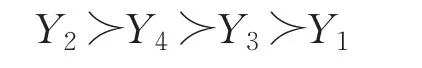
表明高新技術企業Y2在風險評估方面評價結果最好。

為了驗證本文方法的有效性，計算得權重ω=(0.15,0.20,0.20,0.30,0.05,0.10)，利用文獻[22]中的區間Pythagorean模糊加權平均（IVPF-WAA）算子，對各個方案的信息進行集結，并通過各個方案的得分獲得排序結果，與本文方法比較如表2所示。

由表2，兩種方法得到的排序結果完全一致，表明了本文方法的有效性。但本文的決策方法體現了反復、不斷地對決策意見進行協調和修正的一種動態過程，優于IVPF-WAA集結算子。雖然文獻[13]提出了一種交互式決策方法，但該方法只適用于評價值由直覺模糊數刻畫，即要求隸屬度與非隸屬度之和小于等于1，而對于本文中的評價值由區間Pythagorean模糊數刻畫的決策問題，文獻[13]的方法無法解決。由此表明，本文方法具有一定的優越性，更適合于復雜環境下的決策。

5 結束語

交互式決策是多準則決策的一個重要研究內容，在實際決策過程中，由于環境的復雜性和人的認知評價信息往往帶有不確定性，本文在準則權重信息部分已知情況下，利用區間Pythagorean模糊數的得分函數確定每個方案的加權得分向量、區間Pythagorean模糊正理想方案的加權得分向量以及區間Pythagorean模糊負理想方案的加權得分向量，進而給出方案滿意度的概念，并且建立關于準則權重的最優化模型，通過模型求解得到最優準則權向量。考慮到決策者對方案滿意度的主觀要求，依據方案滿意度和決策者給出的滿意度的下限值建立了交互式決策優化模型，通過對方案滿意度的給定和修正來實現人機交互決策，使決策方案滿足決策者的要求，并使各方案盡可能達到最優狀態，豐富了Pythagorean模糊多準則決策的研究內容。本文的決策是在屬性權重數學表達式集合已知的情形下進行的，后續的研究將結合實際問題背景進一步分析確定權重約束。