猶豫梯形模糊算子在多屬性決策中的應用

于 倩，侯福均

1.重慶科技學院 工商管理學院，重慶 401331

2.北京理工大學 管理與經濟學院，北京 100081

1 引言

近年來，隨著社會的快速發展，以及環境的日益復雜，決策的不確定性大大增強，因此模糊多屬性決策越來越受關注。自從Zadeh[1]于1965年提出模糊集的概念之后，其逐漸成為處理模糊信息的有效工具。之后，人們又相繼提出了模糊集的幾種廣義形式，包括粗糙集[2]、2型模糊集[3]、區間模糊集[4]、直覺模糊集[5]、區間直覺模糊集[6]等。

在很多現實決策問題中，決策者在做決策時通常在幾個可能值之間猶豫不決，并且不同的決策者給出的方案評價值通常是不同的。基于以上情況，Torra[7]給出了模糊集的另一種廣義形式，即猶豫模糊集（Hesitant Fuzzy Set，HFS）。猶豫模糊集被提出后，即受到了學者的廣泛關注[8-11]。Xu和Xia[12]定義了猶豫模糊信息的熵和交叉熵，并分析了熵、交叉熵和相似度之間的關系。Zhou等[13]根據Hamacher算子提出了猶豫模糊Hamacher加權平均（Hesitant Fuzzy Hamacher Weighted Average，HFHWA）算子、猶豫模糊Hamacher有序加權平均（Hesitant Fuzzy Hamacher Ordered Weighted Average，HFHOWA）算子和猶豫模糊Hamacher混合平均（Hesitant Fuzzy Hamacher Hybrid Average，HFHHA）算子等。針對屬性間存在關聯的猶豫模糊多屬性決策問題，Zhu和Xu[14]將BM算子拓展到猶豫模糊集環境下，提出了猶豫模糊Bonferroni平均（Hesitant Fuzzy Bonferroni Mean，HFBM）算子和考慮元素權重的加權猶豫模糊Bonferroni平均（Weighted Hesitant Fuzzy Bonferroni Mean，WHFBM）算子。Zhu等[15]基于幾何Bonferroni平均（Geometric Bonferroni Mean，GBM）和Choquet積分提出了猶豫模糊幾何Bonferroni平均（Hesitant Fuzzy Geometric Bonferroni Mean，HFGBM）算子、猶豫模糊Choquet幾何Bonferroni平均（Hesitant Fuzzy Choquet Geometric Bonferroni Mean，HFCGBM）算子、加權猶豫模糊幾何Bonferroni平均（Weighted Hesitant Fuzzy Geometric Bonferroni Mean，WHFGBM）算子和加權猶豫模糊Choquet幾何Bonferroni平均（Weighted Hesitant Fuzzy Choquet Geometric Bonferroni Mean，WHFCGBM）算子。

然而在現實的決策過程中，由于很多決策問題具有模糊性和復雜性，方案的評價值、屬性權重以及專家對決策問題的認知等存在著不能完全確定或者難以用定量數值形式來表示的現象，因此基于梯形模糊數[3]和猶豫模糊集[7]，提出了猶豫梯形模糊集的定義。給出猶豫梯形模糊數的運算法則，進而定義猶豫梯形模糊加權平均（Hesitant Trapezoid Fuzzy Weighted Average，HTrFWA）算子和猶豫梯形模糊加權幾何（Hesitant Trapezoid Fuzzy Weighted Geometric，HTrFWG）算子，構建猶豫梯形模糊數的得分函數，給出猶豫梯形模糊數的排序方法，并將其應用在多屬性決策領域。

2 預備知識

定義1設X為一非空集合，則定義在集合上的猶豫梯形模糊集可用如下形式表示：

定義2 設是三個猶豫梯形模糊元素，且 λ＞0，則其運算規則如下：

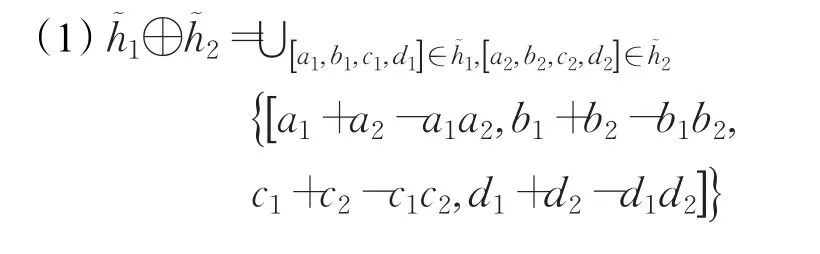
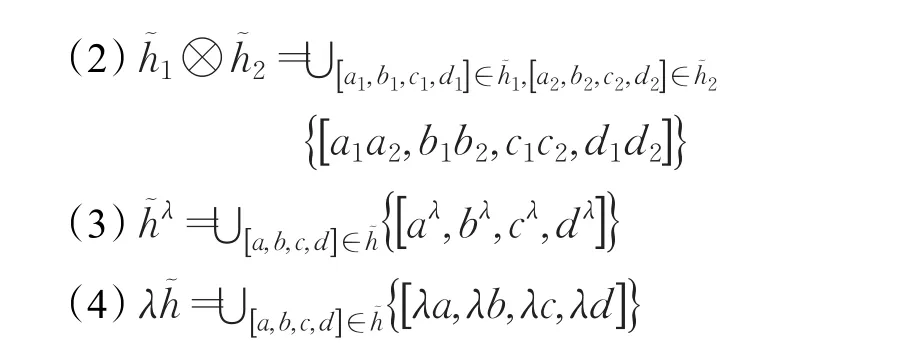
定義3設一個猶豫梯形模糊元素為，則 s(h?)=稱為?的得分函數，其中是?中梯形模糊數的個數。是在區間[0,1]的梯形模糊數。對于兩個猶豫梯形模糊元素和,如果則如果，則對于和的大小，可以用以上方法來進行比較。

基于猶豫梯形模糊集的運算規則，提出了一系列的猶豫梯形模糊集結算子。

定義4設為集合X上的一組猶豫梯形模糊元素，則猶豫梯形模糊加權平均（HTrFWA）算子定義為：

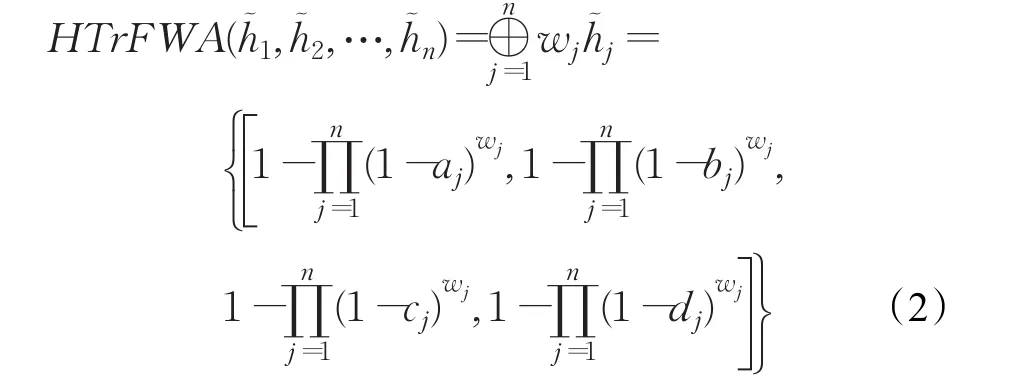
定理1（冪等性） 設為一組猶豫梯形模糊元素，如果任一都相等，如對于所有 j，有，且，則：

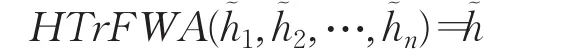
證明如果任意 j,h?j=h?，有：

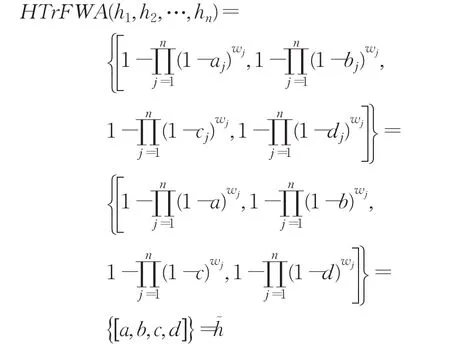
定理2（有界性） 設為一組猶豫梯形模糊元素，令其中，則：

證明有則：

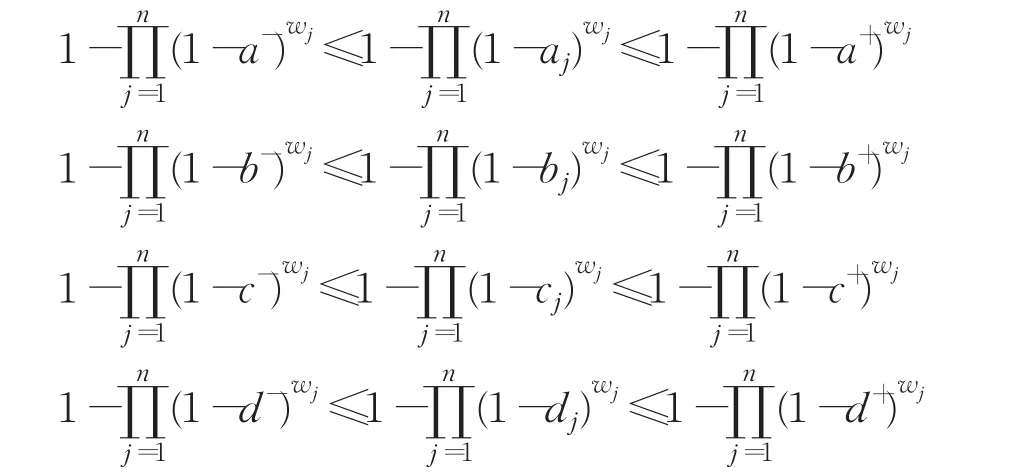
3 猶豫梯形模糊集結算子

定理3（單調性）設和n)為兩組猶豫梯形模糊元素，如果對于所有的 j(j=1,2,…,n)，存在，則：

證明由于，可得：

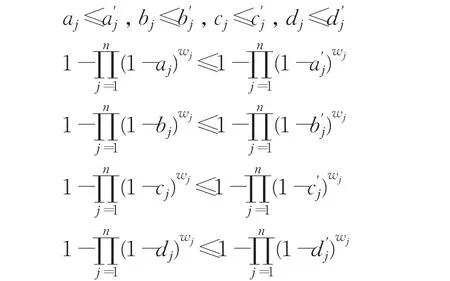
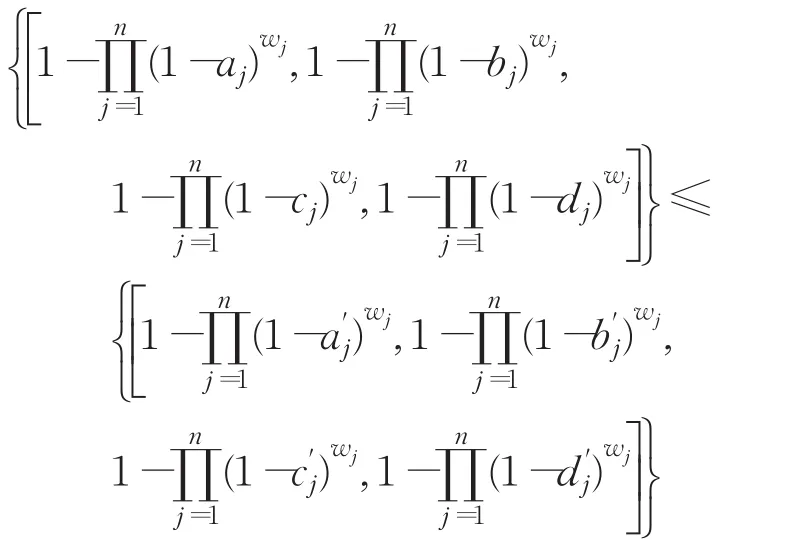
然后

定義5設為集合X上的一組猶豫梯形模糊元素，則猶豫梯形模糊加權幾何（HTrFWG）算子定義為：

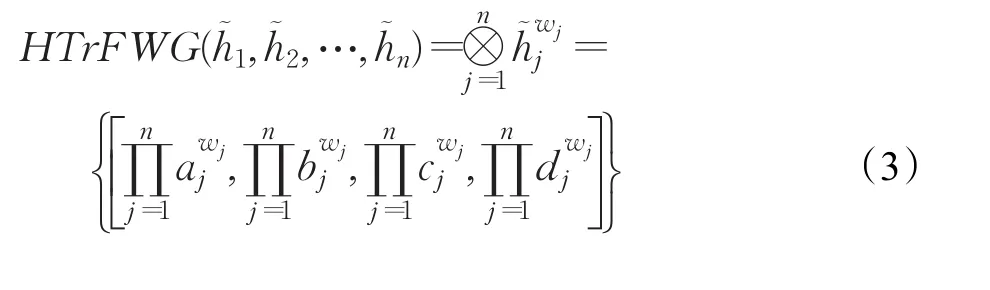
定理4（冪等性） 設為一組猶豫梯形模糊元素，如果任一都相等，即對于所有的 j有?，且，則：

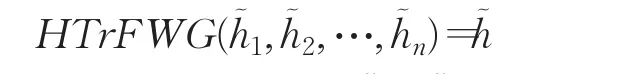
證明如果任意，有：

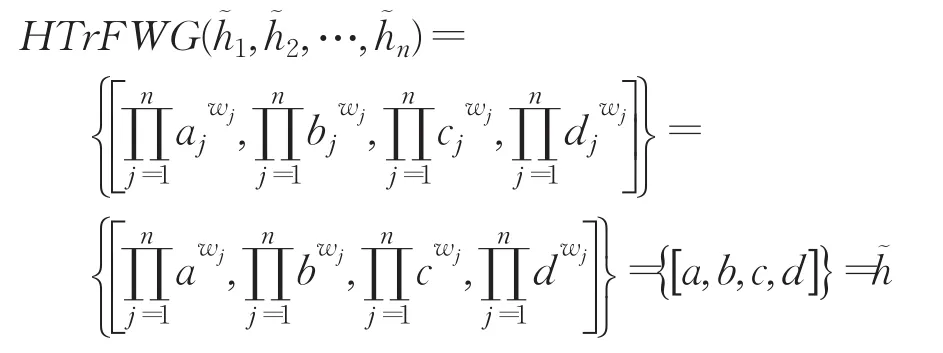
定理5（有界性） 設為一組猶豫梯形模糊元素，令其中a，則：

證明有則：

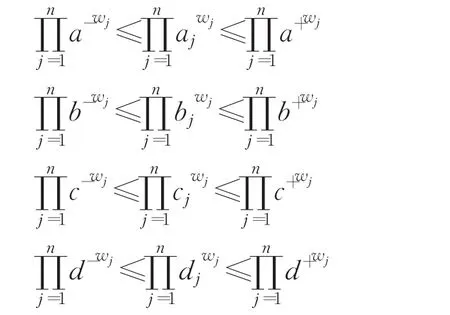
定理6（單調性） 設和n)為兩組猶豫梯形模糊元素，如果對于所有的 j(j=1,2,…,n)，有，則：

證明由于可得：

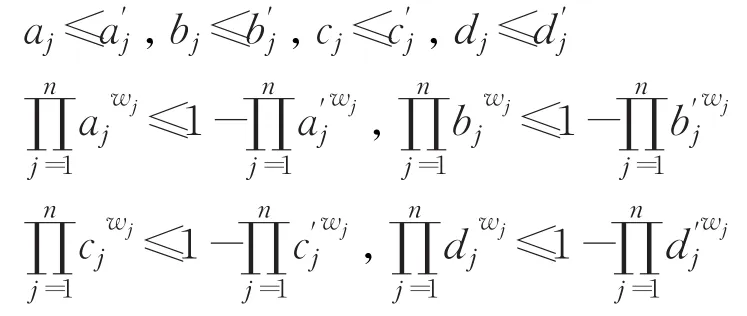
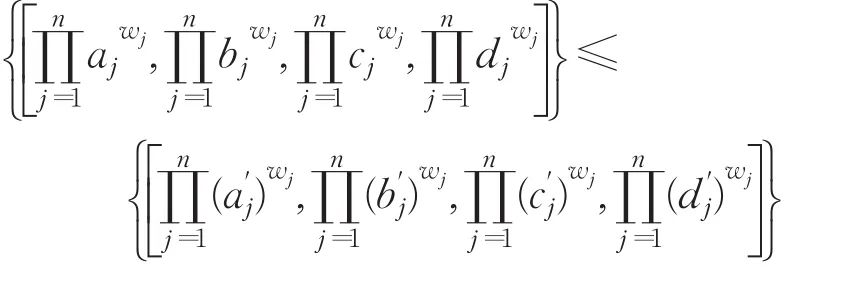
然后

考慮到猶豫梯形模糊數的有序位置存在具有不同權重的情況，因此定義了猶豫梯形模糊有序加權平均（Hesitant Trapezoid Fuzzy Ordered Weighted Average，HTrFOWA）算子和猶豫梯形模糊有序加權幾何（Hesitant Trapezoid Fuzzy Ordered Weighted Geometric，HTrFOWG）算子。

定義6設為集合X上的一組猶豫梯形模糊元素，則猶豫梯形模糊有序加權平均（HTrFOWA）算子定義為：

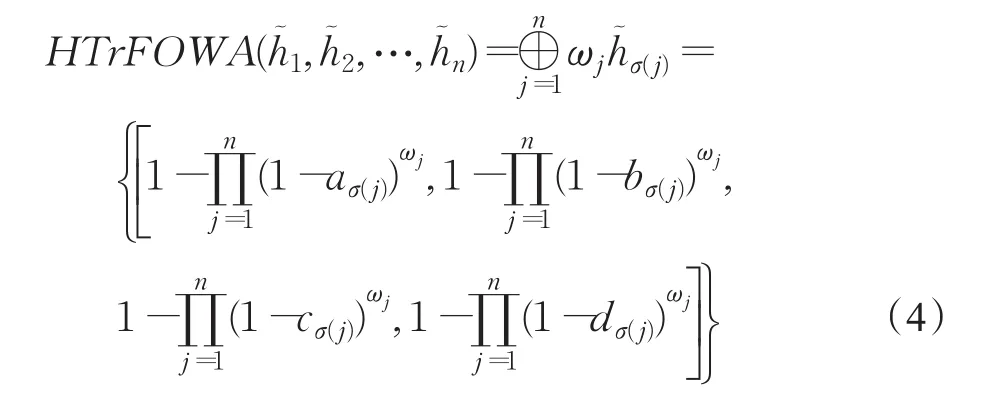
其中，(σ(1),σ(2),…,σ(n))是 (1,2,…,n)的置換，且對于所有的 j，滿足；ω=(ω1,ω2,…,ωn)T是位置權重向量，且

定理7（冪等性）設為一組猶豫梯形模糊元素，如果任一都相等，即對于所有 j，存在?且，則：

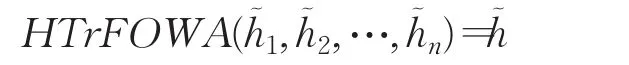
定理8（有界性）設為一組猶豫梯形模糊元素，令其中，，則：

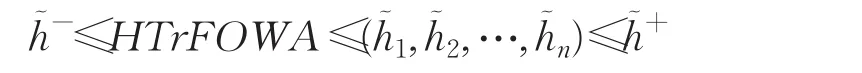
定理9（單調性）設和,n)為兩組猶豫梯形模糊元素，如果對于所有的 j(j=1,2,…,n)，有，則：

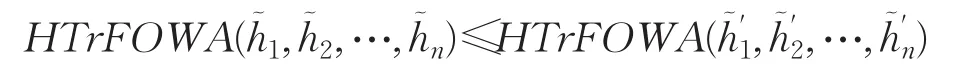
定義7設為集合X上的一組猶豫梯形模糊元素，則猶豫梯形模糊有序加權幾何（HTrFOWG）算子定義為：

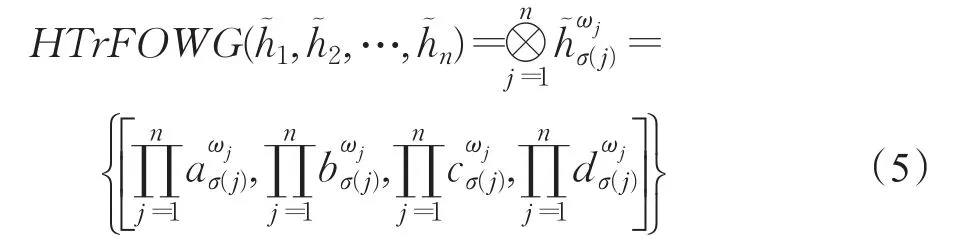
其中，(σ(1),σ(2),…,σ(n))是 (1,2,…,n)的置換，且對于所有的 j，滿足；ω=(ω1,ω2,…,ωn)T是位置權重向量，且

定理10（冪等性）設為一組猶豫梯形模糊元素，如果任一都相等，即對于所有 j，有，則：

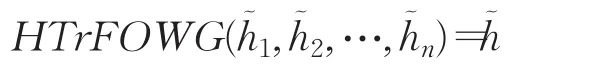
定理11（有界性）設為一組猶豫梯形模糊元素，令其中，則：

定理12（單調性）設和n)為兩組猶豫梯形模糊元素，如果對于所有的 j(j=1,2,…,n)，有，則：

從以上定義可知，HTrFWA和HTrFWG算子考慮的是猶豫梯形模糊數本身的權重，而HTrFOWA和HTrFOWG算子考慮的是猶豫梯形模糊數有序位置的權重。這兩種算子都沒有綜合考慮到上述兩方面，為了解決這一缺點，定義了猶豫梯形模糊混合平均（HTrFHA）算子和猶豫梯形模糊混合幾何（HTrFHG）算子。

定義8設為集合X上的一組猶豫梯形模糊元素，w=(w1,w2,…,wn)T為其權重向量，且則猶豫梯形模糊混合平均（HTrFHA）算子定義為：

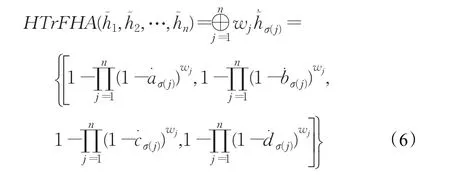
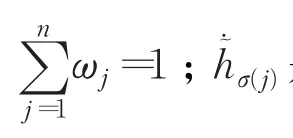
定義9設為集合X上的一組猶豫梯形模糊元素，w=(w1,w2,…,wn)T為其權重向量，且是第 j大的加權猶豫梯形模糊元素，且則猶豫梯形模糊混合幾何（HTrFHG）算子定義為：

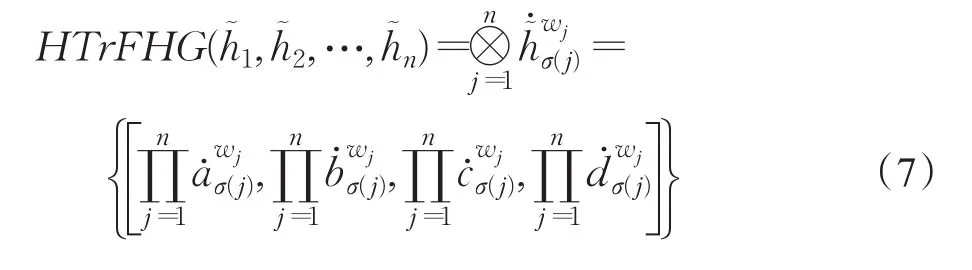
其中，ω=(ω1,ω2,…,ωn)T為位置權重向量，且 ωj≥0，是第 j大的加權猶豫梯形模糊元素，且

4 基于HTr FWA和HTr FWG算子的猶豫梯形模糊多屬性決策方法

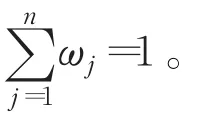
下面介紹基于HTrFWA和HTrFWG算子的猶豫梯形模糊多屬性決策方法的具體步驟。

步驟1.1利用給定的猶豫梯形模糊矩陣和HTrFWA算子，計算得出方案Ai的綜合猶豫梯形模糊評價值h?i(i=1,2,…,m)。

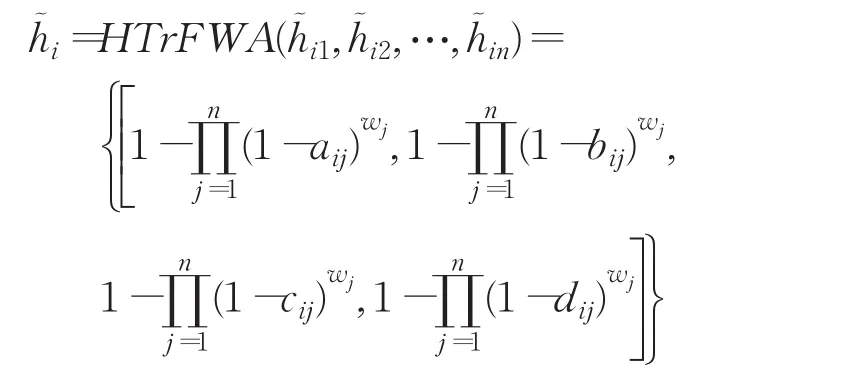
步驟1.2利用給定的猶豫梯形模糊矩陣和HTrFWG算子，計算得出方案Ai的綜合猶豫梯形模糊評價值h?i(i=1,2,…,m)。

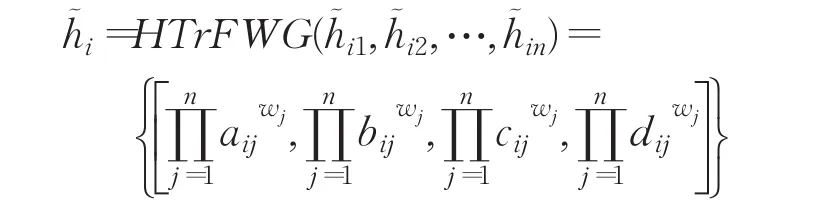
步驟2 計算的得分值

步驟3對進行排序。根據的排序大小，選擇相應的最優方案。

5 算例分析

對于一個生產型企業選擇綠色供應商問題，假設現有5個綠色供應商Ai(i=1,2,3,4,5)，分別從如下4個屬性Cj(j=1,2,3,4)去評價：C1產品競爭力，C2合作與發展潛力，C3供應商競爭力，C4綠色績效。w=(0.2,0.4,0.1,0.3)T是其權重向量。專家給出各個備選綠色供應商在上述4個屬性下的評價值，以猶豫梯形模糊集的形式表示，各個屬性評價值構成如下猶豫梯形模糊決策矩陣

為了選擇最優供應商，利用猶豫梯形模糊加權平均（HTrFWA）算子和猶豫梯形模糊加權幾何（HTrFWG）算子來解決基于猶豫梯形模糊集環境下的綠色供應商評價問題。具體步驟如下：

步驟1.1利用HTrFWA算子將所有的猶豫梯形模糊信息集結成綜合猶豫梯形模糊值為例：

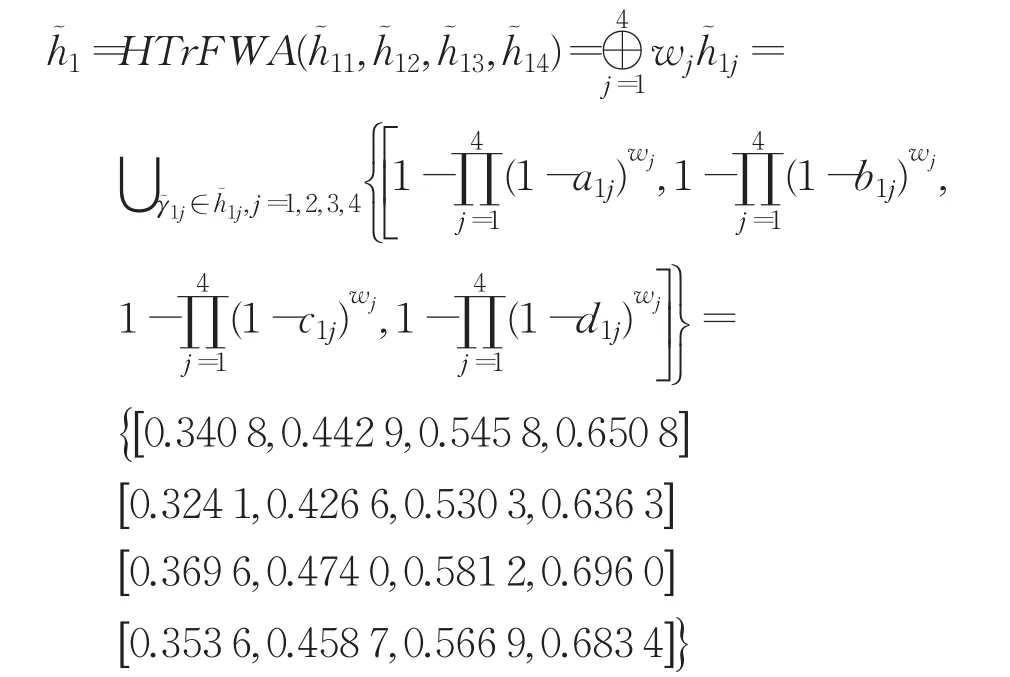
步驟2計算綜合猶豫梯形模糊值的得分值

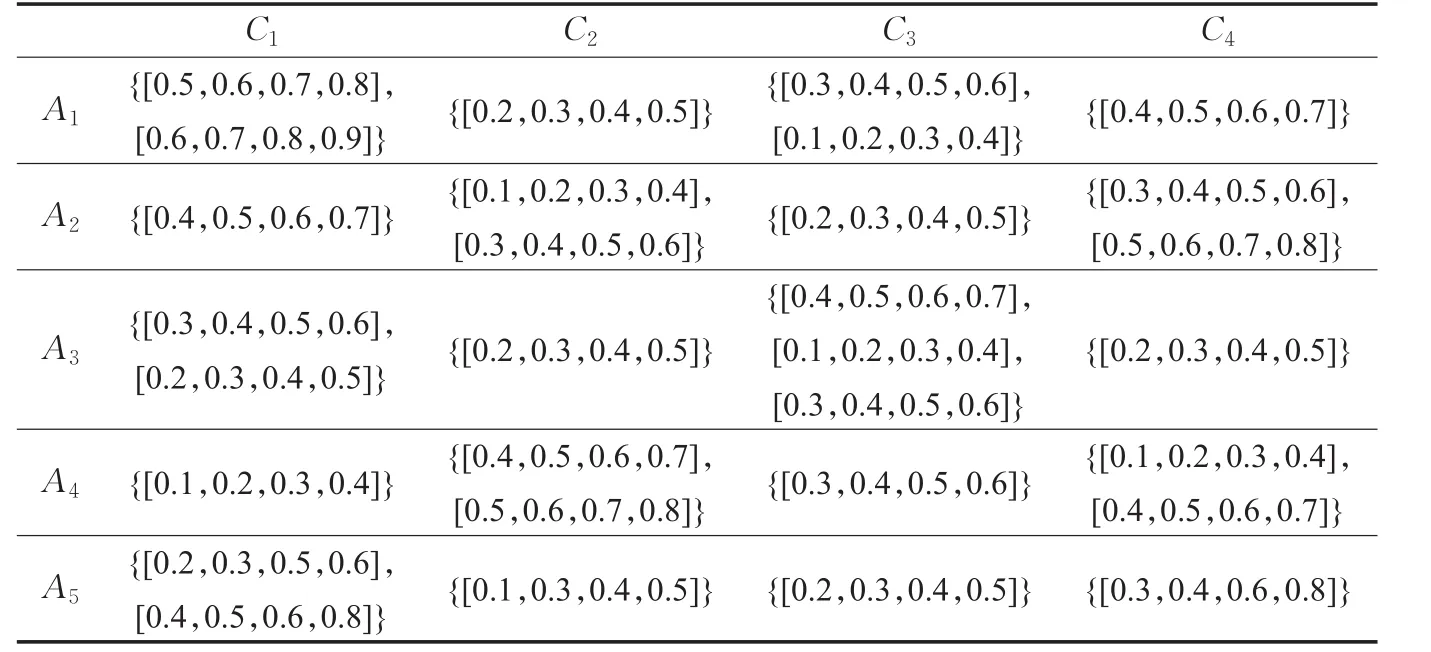
表1 猶豫梯形模糊矩陣

步驟3根據各個得分值的大小，對各個供應商進行排序，，因此最優的綠色供應商是A1。

接下來，利用HTrFWG算子來計算各方案的綜合猶豫梯形模糊值，步驟如下：

步驟1.2利用HTrFWG算子來計算綜合猶豫梯形模糊值以為例：

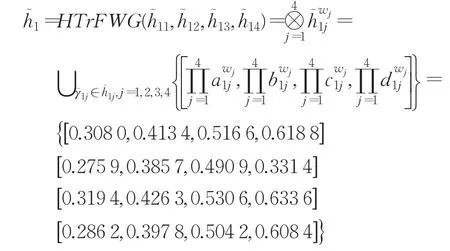
步驟2計算各綜合猶豫梯形模糊值的得分值

步驟3根據各得分值的大小，對各綠色供應商Ai(i=1,2,3,4,5)進行排序，，因此最優供應商仍是A1。

通過以上分析可以看出，雖然利用這兩種算子各供應商的最終排序有輕微不同，但綠色供應鏈中的最優供應商仍是A1。

基于不同算子的排序結果如表2所示。

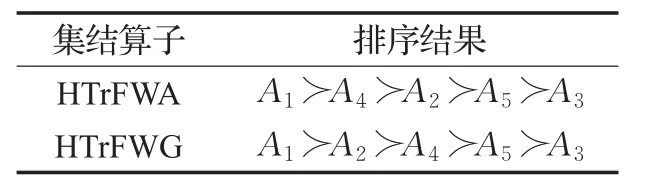
表2 基于不同算子的排序結果

6 結束語

本文基于猶豫模糊集和梯形模糊數，定義了猶豫梯形模糊集。首先，給出猶豫梯形模糊數的運算法則，探討猶豫梯形模糊加權平均（HTrFWA）算子和猶豫梯形模糊加權幾何（HTrFWG）算子。考慮到猶豫梯形模糊數的有序位置存在具有不同權重的情況，定義了猶豫梯形模糊有序加權平均（HTrFOWA）算子和猶豫梯形模糊有序加權幾何（HTrFOWG）算子，并討論了其相應的運算定理。其次，構建猶豫梯形模糊數的得分函數，并給出猶豫梯形模糊數的排序方法。最后，提出了基于HTrFWA算子和HTrFWG算子的猶豫梯形模糊多屬性決策方法，并通過實例進行驗證。