基于神經網絡的BFe30-1-1銅合金的本構關系模型

馬艷霞，韓茂盛，劉樂樂，梁 晨

（中國船舶重工集團公司第七二五研究所，河南 洛陽 471000）

BFe30-1-1銅合金具有良好的塑形成型性能、焊接性能和超強的抗腐蝕性能，在海洋工業中得到廣泛的應用，主要用于制造艦船的構件，同時BFe30-1-1銅合金也是制作冷凝管的主要材料，在電力、化工等行業也有廣泛的應用，具有廣闊的應用市場[1-3]。Fe30-1-1銅合金主要以管材的形式應用，而管材成形主要采用熱擠壓的方法，金屬的熱變形行為是確定擠壓工藝的理論依據，因此研究材料熱變形對這種高溫成形工藝的制定和模具材料的選擇具有重要作用[5,6]。

材料的高溫變形本構關系對描述材料在熱加工過程中應力與變形工藝參數之間的關系，是變形應力參數計算、實現過程數值模擬的必要基礎。建立材料本構關系時，傳統方法一般通過有限的實驗結果進行回歸，獲得一些經驗公式然而，材料在高溫變形過程中內部的動態響應是一個十分復雜的過程，影響流變應力的因素較多且呈現高度非線性的特征。因此采用傳統的方法建立的本構模型不能精確的表現出材料復雜的真實變形情況，從而降低了模型的精度。人工神經網絡是由模擬人腦神經系統學習外界環境信息的過程而發展起來的一種人工智能信息處理系統，具有較高的容錯性、良好的自組織、自學習、自適應和很強的聯想記憶功能，是新一代信息處理工具。BP（Back Propagation）神經網絡是普遍使用的一種預報模型，非常適合于解決復雜的非線性問題。利用BP神經網絡對材料塑形變形過程進行建模，可在很大程度上克服傳統回歸方法的局限性。國內外利用人工神經網絡算法進行材料本構關系模型建立的研究已經很多，但是未見到其在BFe30-1-1銅合金上的應用研究[7-9]。

本研究在Gleeble-3500熱模擬機上，采用圓柱體高溫壓縮實驗，得到BFe30-1-1銅合金在不同變形工藝參數條件下的應力值，并以此實驗數據為學習樣本，利用BP神經網絡建立BFe30-1-1合金的本構關系模型，并對其進行誤差分析，為合理制定BFe30-1-1合金熱加工工藝提供指導依據。

1 實驗

實驗用原材料為BFe30-1-1銅合金鑄錠，其化學成分見表1。將鑄錠加工成?10mm×15mm的圓柱試樣并經過950℃進行均勻化處理后，在Gleeble-3500熱模擬實驗機上進行壓縮。實驗過程中，在壓頭與試樣兩端接觸處夾一層石墨片進行潤滑，以減少摩擦對應力狀態的影響。合金的變形溫度T設定為800、850、900、950℃，應變速率分 別為 0.1、1、10、20s-1，總壓縮應變量為0.60。加熱階段的升溫速率為10℃/s，保溫3min，壓縮結束后快速水冷。

表1 實驗合金化學成分/Wt%

2 BFe30-1-1銅合金高溫流變行為

圖1為BFe30-1-1銅合金熱壓縮變形時的真應力應變曲線。從圖中可以看出，當變形溫度和應變速率一定時，流變應力隨應變的增加先迅速增大，在某一臨界應變處達到應力峰值，之后流變應力隨著應變的增加保持平穩，具有穩態變形的特征，在低應變速率和高變形溫度時，流變應力隨著應變的增加呈現減小趨勢。這是因為在變形過程中，變形前期加工硬化占主導地位，中間只發生了部分動態回復與動態再結晶，塑性變形比較困難。隨著變形量的增大，動態回復與動態再結晶速度加快，軟化作用逐漸增強。從圖中還能發現，流變應力隨著溫度的降低而增大，隨著應變速率的增大而增大，這是由于隨著溫度的升高，合金動態再結晶的形核率和長大速率都有所增加，進而使動態再結晶軟化作用加強。同時，溫度的升高帶來的材料臨界剪切應力下降，可能出現更多的滑移系，這些都會導致流變應力的下降。然而，隨著應變速率的增大，變形時間縮短導致位錯和位錯攀移發展不充分，影響了回復效果，同時高應變速率使位錯增值的速度增大，引起短時間內的位錯堆積，使得位錯運動所需驅動力也相應增大，從而導致應力增大。

3 BFe30-1-1銅合金神經網絡本構模型

3.1 模型建立

BP神經網絡模型是一種誤差反向傳播的多層前饋式網絡模型，包括輸入層、隱含層和輸出層，輸入層節點數取決于輸入參數的個數，輸出層節點數取決于輸出參數的個數，隱含層可以包含單層或多層的神經元節點，其節點數取決于具體研究對象，而同層節點間沒有任何耦合。圖2為BP神經網絡結構圖，從圖中可以看出，輸入信號通過層之間的權值w調節，由輸入節點傳入各隱層節點，最后到達輸出節點，通過誤差比較修正各層的權值后再反向傳播，直至達到目標誤差后傳出。由于連接權值w不同，輸入的信號被放大、衰減或抑制，除輸入層外，每一節點的輸入為前一層所有節點輸出值的加權和，每一點的激勵輸出值由節點輸入、激勵函數以及偏置量決定，因此該網絡可以實現從輸入到輸出的高度非線性映射。

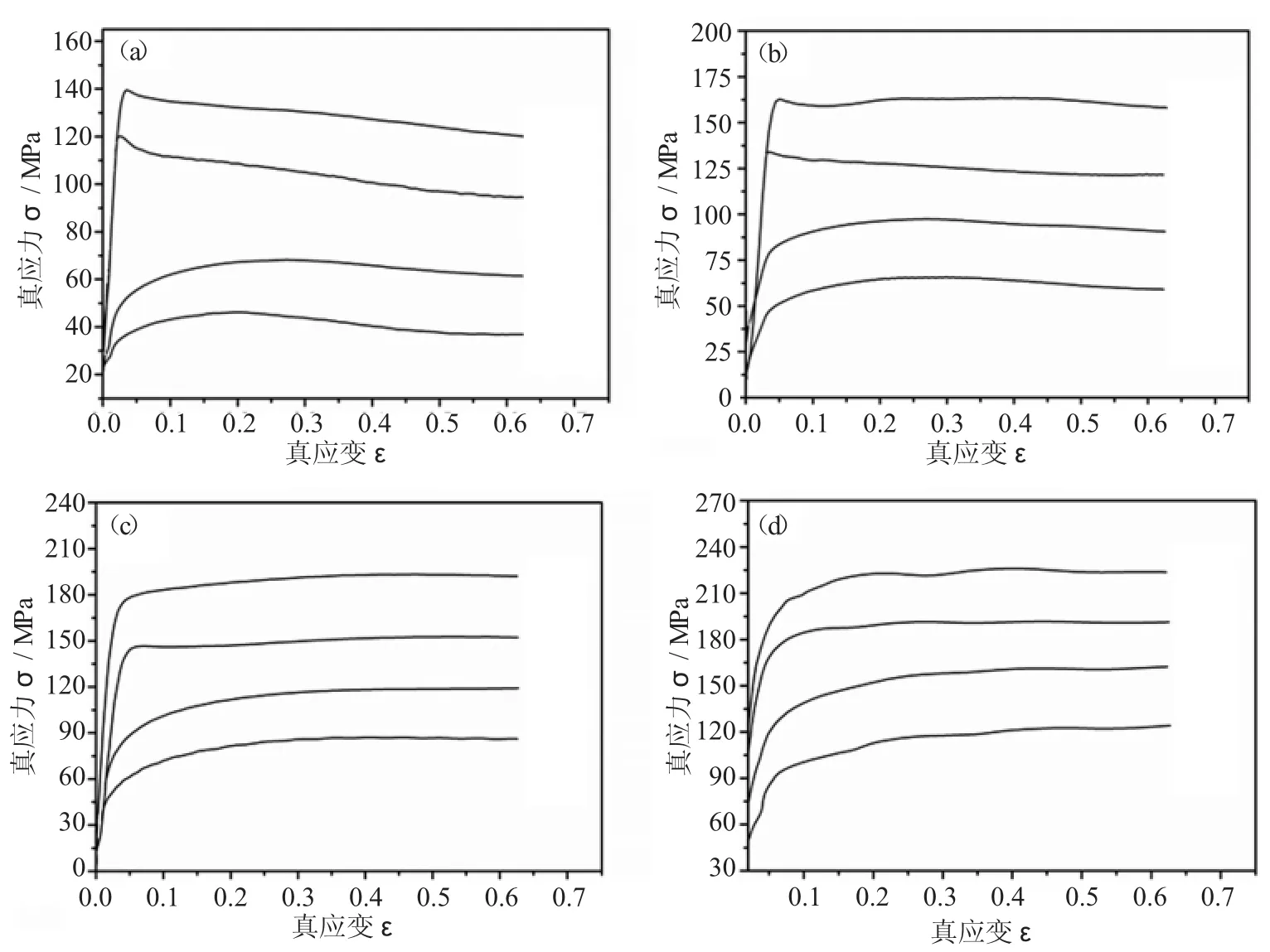
圖1 BFe30-1-1銅合金在不同應變速率下熱壓縮變形的真應力-應變曲線（a）0.1 s-1 （b）1 s-1 （c）10 s-1 （d）20 s-1

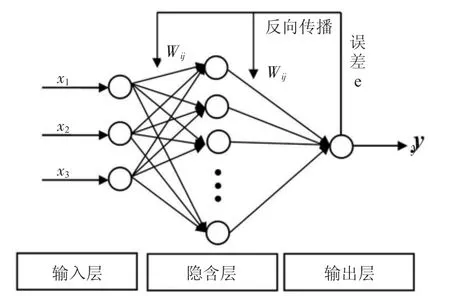
圖2 BP神經網絡模型

第j層的輸出公式可由公式（1）表示。

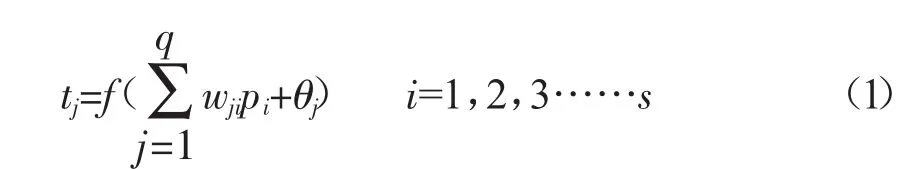
式中，tj為第j層的輸出值；f為第j層地激勵函數；為第i層與j層的連接權值；pi為第i層的輸入值；θj為第j層的偏置量或閥值；s為第j層神經元個數；q為第i層神經元個數。

網絡系統的準確性用系統的均方差來表示，如公式（2）所示。

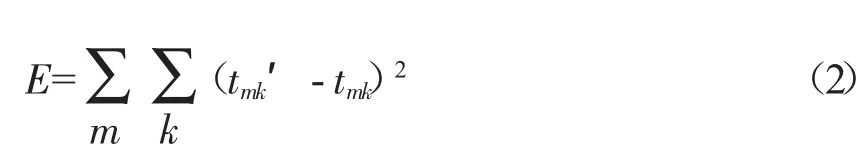
式中，E為系統均方差；m為樣本個數；k為輸出層神經元個數；tmk′為期望輸出值；tmk為實際輸出值。

在網絡學習過程中，若系統均方差未滿足要求則調整權值，然后反向傳回網絡系統重新計算，直至網絡誤差滿足要求或達到指定的學習次數。本文采用三層BP神經網絡模型，輸入層包含變形溫度T、真應變ε和應變速率ε˙三個節點，輸出層為真應力σ。

3.2 數據預處理

從圖1的真應力-應變曲線中選取288個數據分為兩組，其中192個作為訓練樣本，96個用于驗證。由于變形溫度、變形速率和真應變的數值單位不同，數值相差較大，這樣會促使量級大的數值在網絡訓練中起主要作用，影響網絡的判斷，因此在建立網絡之前必須對所有數據進行相關處理，從而去除各數值之間的量綱差異，使所有的數據處于同等重要的位置，此外還可以保證網絡的穩定[10]。

根據BP神經網絡對輸入輸出范圍的要求，按公式（3）對訓練樣本的輸入、輸出參數進行歸一化處理。

式中，X實驗所獲得的原始數據，Xmin和Xmax為原始相應數據的最小值和最大值，X′為參數X歸一化處理后的數值。

3.3 模型訓練

采用Matlab將歸一化后的訓練樣本對BP神經網絡進行訓練，轉移函數為“tan sigmoid”和“pure linear”，訓練函數為“Trainlm”，訓練目標誤差為 10-3。隱含層神經元數目的選擇是一個非常復雜的問題，數目太少會導致訓練出來的網絡容錯性差，不能識別參與未參與訓練的樣本；數目過多會導致學習時間過長，誤差不一定最佳，因此隱含層單元數存在一個最佳值，通常來說，隱含層神經元數目通過經驗公式（3）來確定范圍：

式中，n1為隱含層單元數，m為輸出層神經元數，n為輸入層單元數，a為0～10之間的常數。

為了確定隱藏層的神經元的數量，從兩個神經元開始，采用試錯法進行一一訓練，最終發現當隱含層神經元個數為12時，網絡性能最好。BP網絡模型經過880個循環達到穩定狀態。

3.4 結果分析

如圖3所示，將神經網絡預測得到的流變應力值進行反歸一化處理，并與驗證樣本進行對比。從圖中可以看出，BP神經網絡預測的流變應力與實驗數據的相關性較好，擬合相關系數達到0.9999。

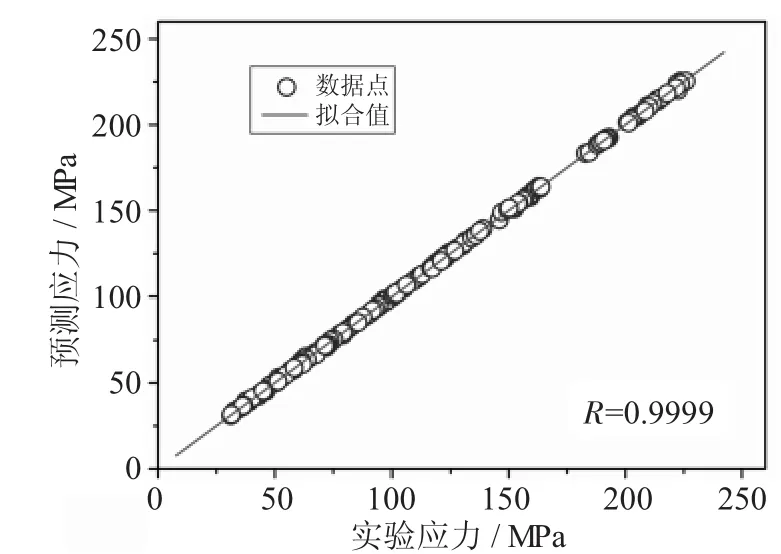
圖3 BP神經網絡模型預測流變應力值與實驗值的關聯性曲線

表2為應變速率為0.1s-1時不同應變、變形溫度下的部分流變應力值與神經網絡模型預測值之間的誤差情況，從表中能夠發現，預測值與實際值非常接近，相對誤差在5%以下。

如圖4所示為采用BP神經網絡模型預測的BFe30-1-1銅合金流變應力與實驗值的對比圖。從該圖中可以看出，采用BP神經網絡模型預測的流變應力值與實驗值吻合良好，而且具有較高的精度。

為全面考察所建立的本構模型的精度，根據公式（4）計算可得到擬合度δ：

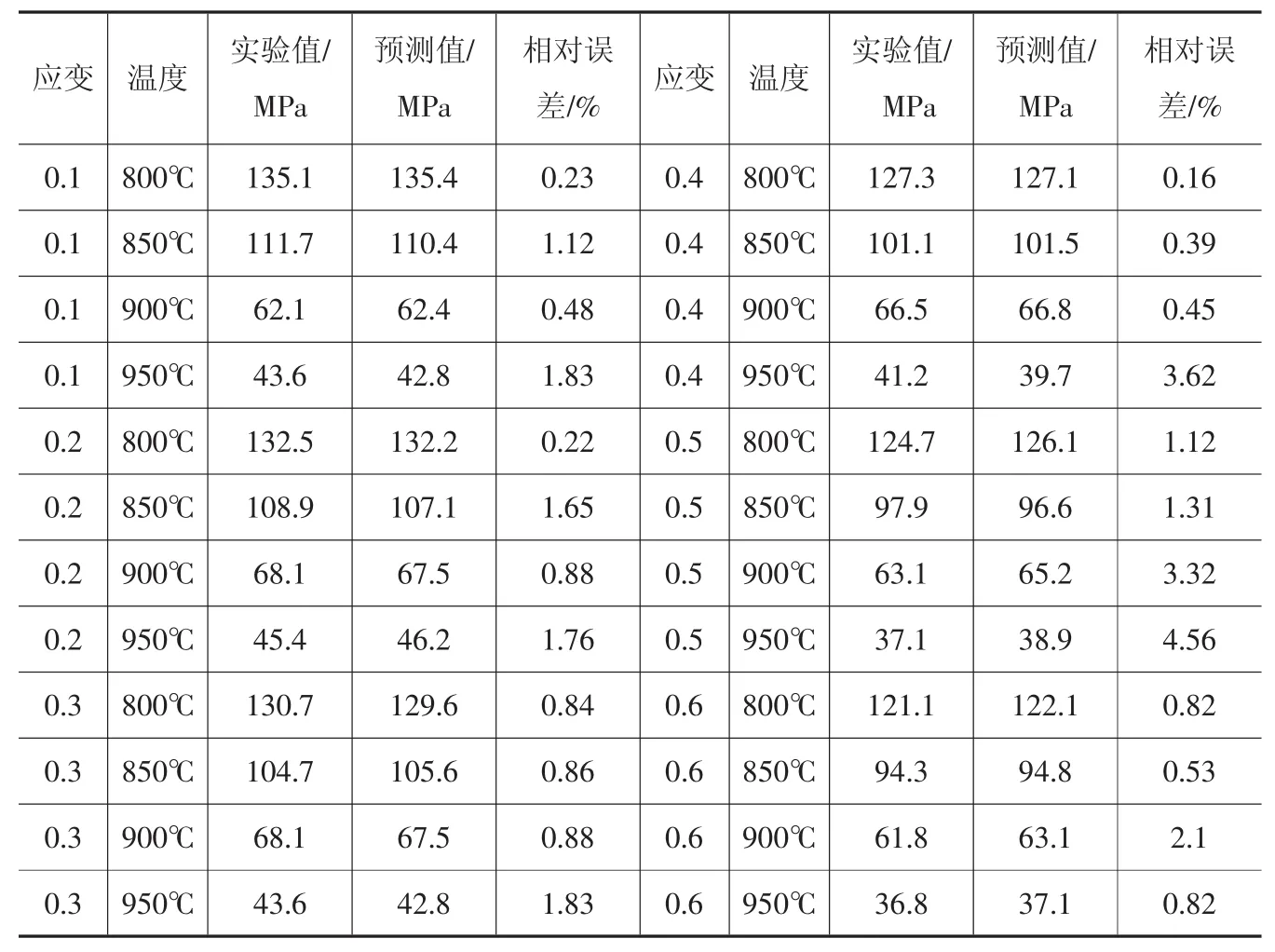
表2 應變速率為0.1s-1時神經網絡模型預測值與實驗值對比

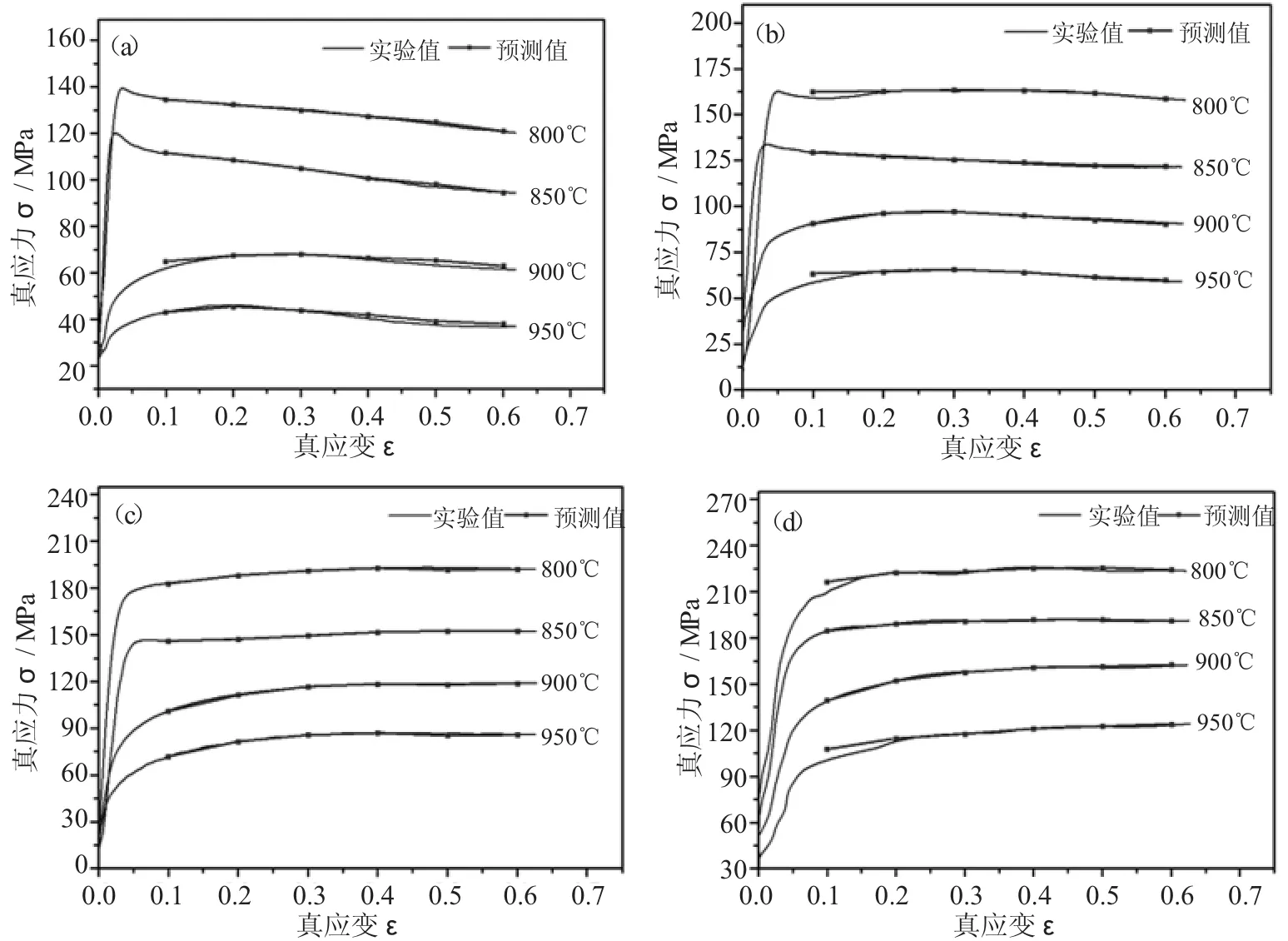
圖4 采用BP神經網絡模型預測的BFe30-1-1銅合金流變應力值與實驗值的對比（a）0.1s-1 （b）1s-1 （c）10s-1 （d）20s-1

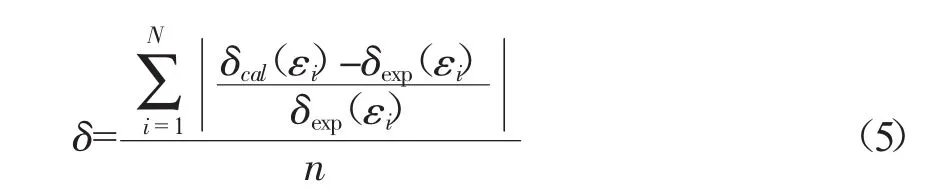
式中，δexp（εi）為流變應力的實驗值，δcal（εi）為通過BP模型計算的預測數據，n為實驗分析數據點的個數。經計算，得到的平均相對誤差為1.65%，進一步證明BP神經網絡模型具有較高的精度，可滿足工程計算要求。

4 結論

（1）通過熱壓縮實驗得到了BFe30-1-1銅合金在應變速率為0.1～20s-1和變形溫度為800～900℃的真應力-應變曲線，發現B30銅合金的流變應力隨著變形溫度的增加而降低，隨著應變速率的增大而增大。

（2）利用BP神經網絡算法，建立了BFe30-1-1銅合金高溫壓縮變形過程的本構關系模型，結果顯示計算值和預測值的擬合相關系數達到0.9999，得到的平均相對誤差為1.65%，表明BP神經網絡模型具有較高的精度，能較好的滿足工程計算的要求。