圓柱鍛件沖孔極限尺寸的參數化預測

葉 明，高錦張，馬武江，王興中

（1.東南大學 材料科學與工程學院，江蘇 南京 211189；2.上海新閔重型鍛造股份有限公司，江蘇 東臺 224200）

在現代工業生產中，大型空心鍛件的使用越來越多，例如在核電行業中，大型空心鍛件應用于主管道鍛件、反應堆壓力容器和蒸汽發生器等，都屬于核島內七大關鍵設備[1-3]。

為了制訂空心鍛件沖孔工藝參數，對圓柱鍛件沖孔極限尺寸進行模擬研究。在圓柱鍛件進行沖孔過程中，較細的沖頭直徑常常會發生彎曲現象，造成鍛件報廢甚至安全事故。這是因為在沖孔時，沖頭的軸向壓力超過了沖頭類長桿件的臨界壓力，發生壓桿失穩現象[4]。

因此，本文以圓柱鍛件沖孔過程為模擬研究對象，主要研究在圓柱鍛件的高徑比在1.0～3.0之間，最小合理沖孔尺寸的變化規律，目的在于尋找任意圓柱鍛件沖孔過程的合理最小沖孔尺寸的范圍，為實際生產提供理論依據，提高安全系數。

1 有限元模型的建立及模擬方案

1.1 有限元模型的建立

本文選用DEFORM-3D有限元模擬軟件分析圓柱鍛件沖孔的鍛造過程，對沖孔工藝進行模擬分析，坯料模型尺寸與實際尺寸以1:1進行建模。其中沖頭選用平底沖頭，在沖頭端部設有圓角r為20mm，如圖1所示。

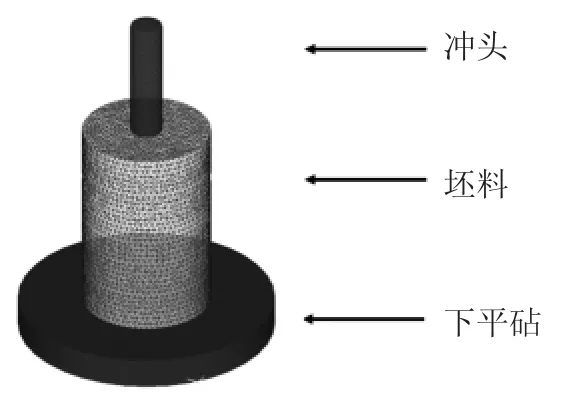
圖1 數值模擬模型

坯料的材料模型是P91耐熱合金鋼，設為塑性體，沖頭及下平砧采用H13鋼，不發生塑性變形，均設置為剛體。由于坯料沖孔過程中心部為主要變形區域，在網格劃分過程中，采用絕對網格劃分，并對主要的變形區域進行網格細分。有限元模型參數設置如表1所示。

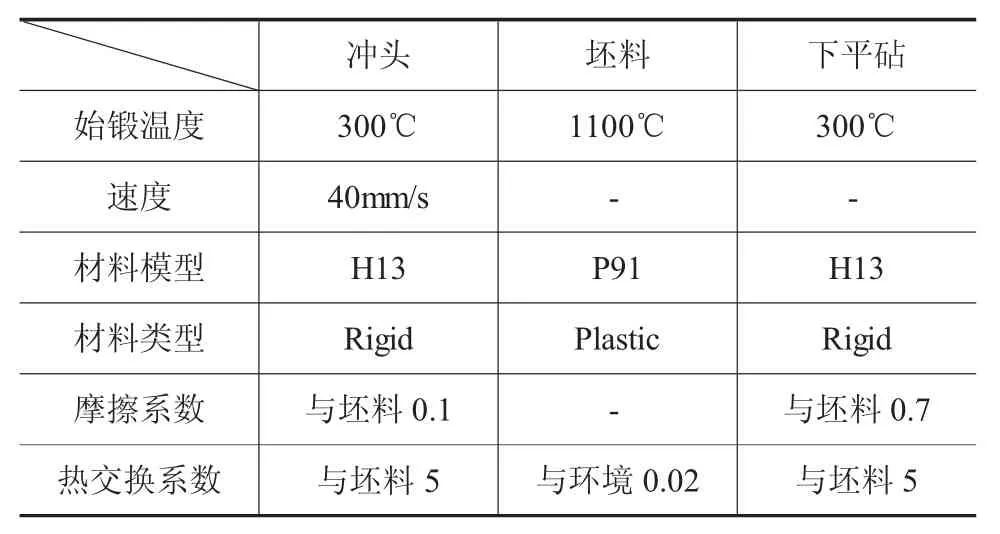
表1 前處理工藝參數的選定

1.2 模擬實驗方案

選取高徑比（H/D）為 1.0、1.5、2.0、2.5 和 3.0 的圓柱鍛件，其中H為圓柱鍛件的高度，D為圓柱鍛件的直徑。在每個高徑比下，選擇幾種坯料尺寸，如表2所示。第一階段為正沖，沖孔深度為坯料高度的一半。同時為方便夾持沖頭，沖頭長度取H/2+200mm。由于圓柱形坯料上下對稱，現只分析坯料一半時的成形過程。

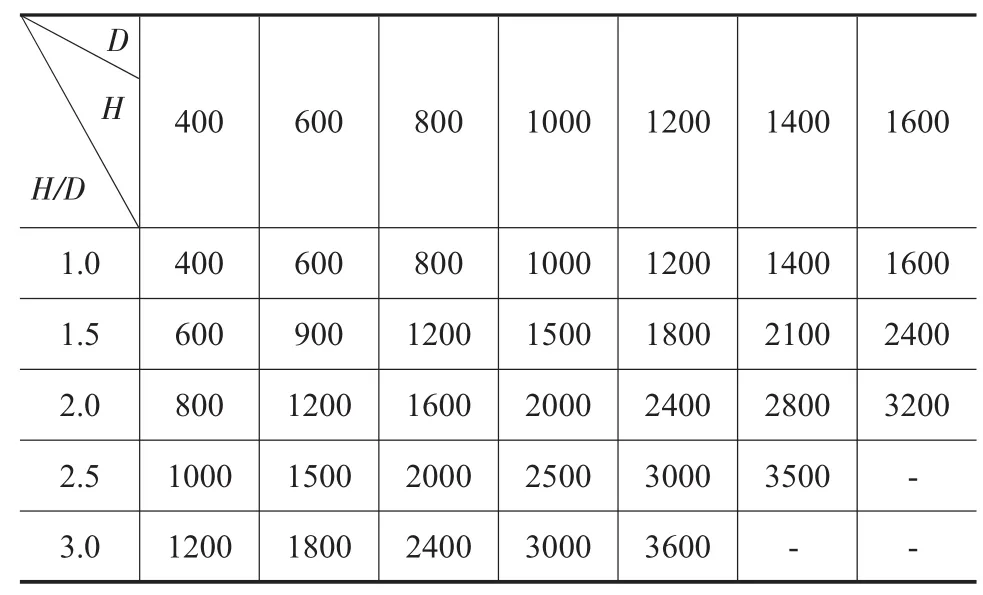
表2 不同H/D下，不同坯料直徑的最大沖孔尺寸/mm

2 圓柱鍛件沖孔尺寸下限的確定

2.1 孔徑比下限的理論基礎

根據選取的圓柱形坯料尺寸，在模擬沖孔過程中保證沖頭不發生失穩的情況下，探究坯料內孔直徑的最小值，定義最小的孔徑比dmin/D。

壓桿穩定計算中，需要采取不同的安全系數。在實際生產中，壓桿的穩定按如下條件計算：

式中：Fcr——臨界載荷；

Fa——工作載荷；

n——壓桿的規定穩定安全系數。

根據文獻[5]，取 n=2。

其中，圓柱形沖頭的臨界載荷Fcr滿足的條件為：

式中：E——沖頭彈性模量；

d——沖頭直徑；

μ——長度系數；

L——沖頭長度。

沖頭采用H13鋼，其彈性模量E=210GPa，壓桿長度系數μ=2。

2.2 圓柱鍛件沖孔尺寸下限的研究

選擇H/D=1.5、直徑D為?1000mm、高度H為1500mm的坯料進行模擬分析。沖頭直徑分別取150mm、200mm、250mm、300mm、350mm、400mm， 對應的孔徑比分別為 0.15、0.20、0.25、0.30、0.35、0.40，沖頭長度均為950mm。得到沖孔的載荷行程曲線如圖2所示。

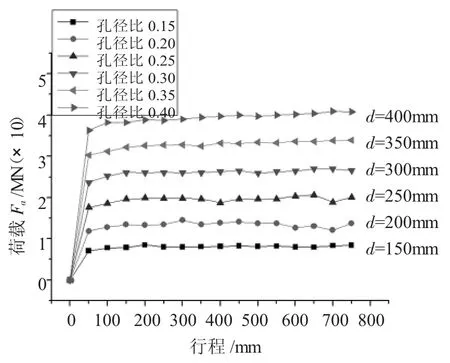
圖2 沖孔時沖頭載荷行程曲線

由圖2可見，對于幾種尺寸的沖頭在沖孔初始階段，沖頭的成形載荷均出現急劇增大，隨著沖頭行程增加，成形載荷均各自趨于穩定值；圖3是在半沖結束的情況下，各種直徑沖頭沖孔的最終成形載荷與沖頭直徑的對應關系曲線圖。由圖3可知最終成形載荷隨著沖頭直徑尺寸增大而增大。

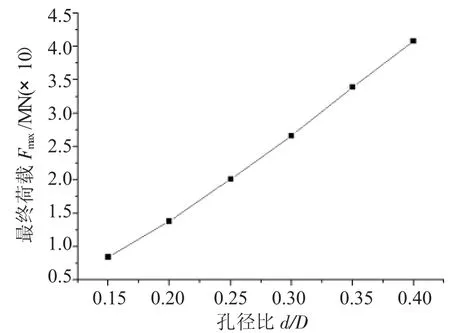
圖3 最終載荷與沖頭直徑關系圖

研究發現最終載荷與沖頭直徑的規律在表2中H/D 為 1.0、1.5、2.0、2.5、3.0 各種情況下依然成立，即高徑比一定及毛坯直徑一定時最終成形載荷均隨著孔徑比的增大而增大。

為了確定沖孔毛坯尺寸為?1000mm×1500mm下的沖孔孔徑比下限，改變沖頭直徑大小，對坯料進行沖孔模擬實驗，提取沖孔過程中的最終成形載荷Fmax。同時根據公式（2）計算的各個尺寸下沖頭的臨界載荷Fcr進行穩定條件處理，得到曲線分析圖4所示。

由圖4可知，在各個沖孔直徑尺寸下沖頭的臨界載荷曲線與2倍的沖頭的穩定載荷曲線相交一點P，其落在橫坐標d處。當沖頭直徑小于d時，Fcr/Fmax≤2，沖頭的臨界載荷值小于2倍的沖頭的穩定載荷，不滿足公式（1），在沖孔過程中會發生失穩現象，造成事故；當沖頭直徑大于d時，即滿足式（1）要求，即沖頭沖孔時不會發生失穩，可以保證生產安全。因此，對應的橫坐標d為穩定沖孔過程的最小沖孔直徑dmin。

圖4 沖孔過程穩定載荷與臨界載荷曲線

3 不同H/D下，圓柱鍛件沖孔的尺寸下限

依次選取表2中坯料尺寸數據，分別對高徑比H/D為 1.0、1.5、2.0、2.5、3.0 的圓柱鍛件進行沖孔模擬實驗，計算相應的坯料沖孔尺寸的下限值，如表3～表7。同時為了更直觀地了解最小沖頭直徑dmin與坯料直徑D之間的關系，將其繪制成曲線，并進行一次線性擬合，如圖5～圖9所示。

由圖5、圖6、圖7、圖8、圖9可知，在高徑比在1.0、1.5、2.0、2.5 和 3.0 時，模擬結果和相對應的擬合曲線重合度較高。因此，在一定高徑比下圓柱鍛件沖孔最小沖頭直徑與坯料直徑參數化關系的建立具有理論基礎。

表3 H/D=1.0/mm

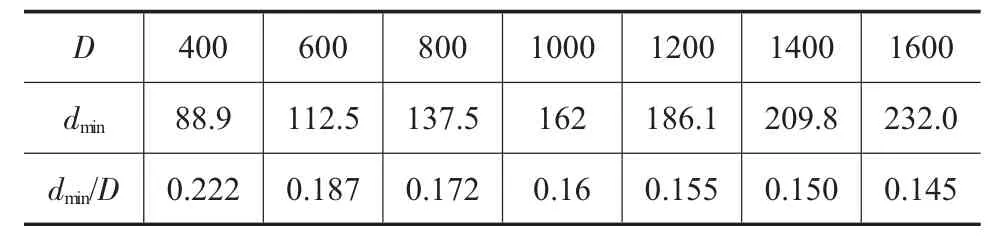
表4 H/D=1.5/mm

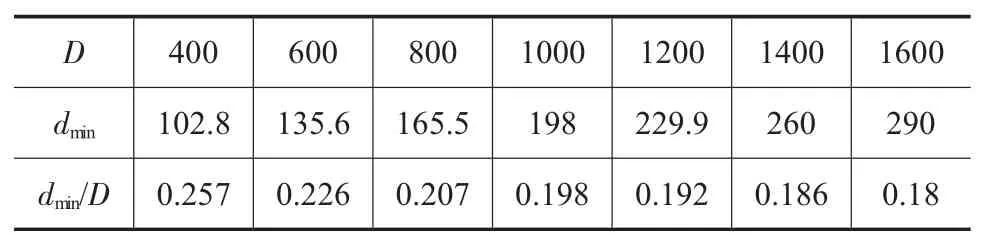
表5 H/D=2.0/mm

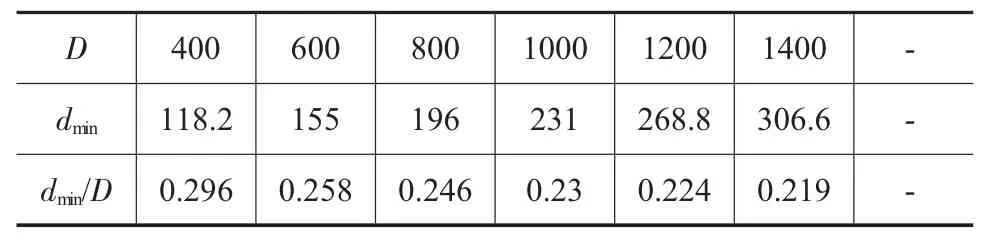
表6 H/D=2.5/mm

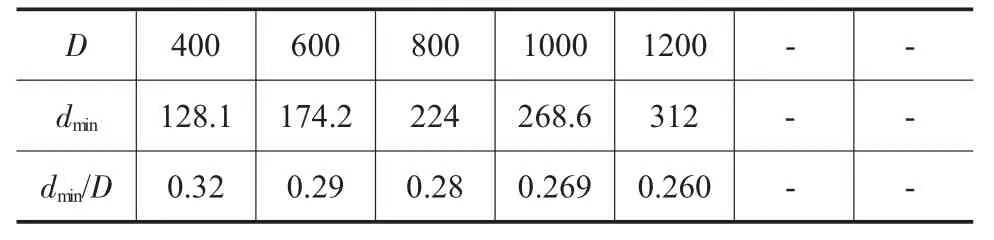
表7 H/D=3.0/mm

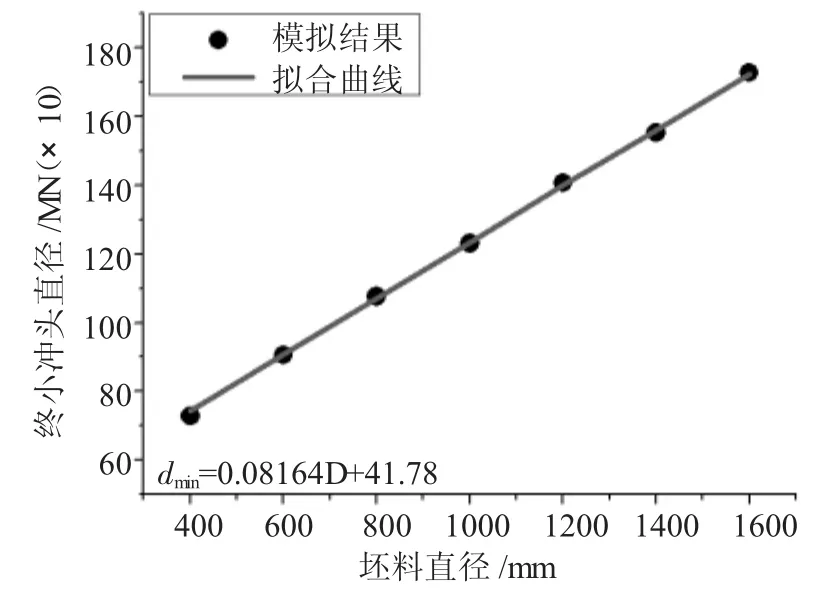
圖5 H/D=1.0最小沖頭直徑隨坯料直徑的變化關系

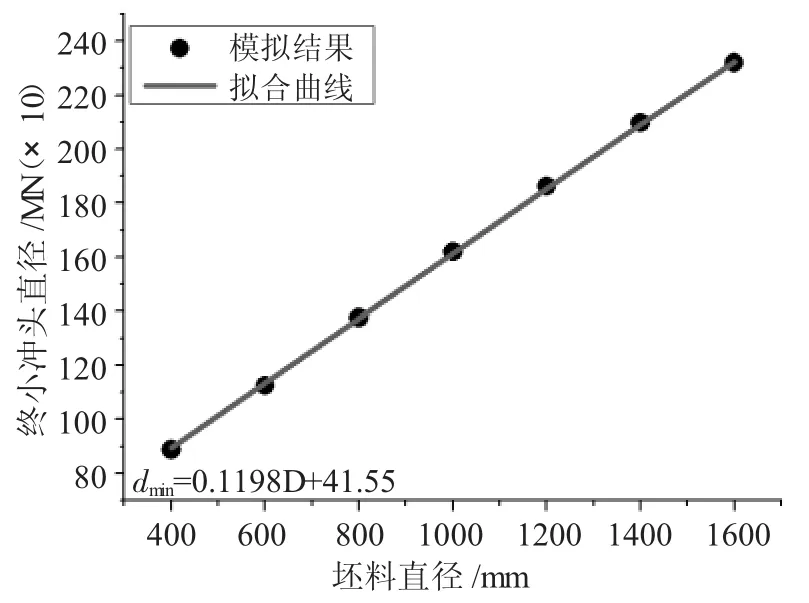
圖6 H/D=1.5最小沖頭直徑隨坯料直徑的變化關系

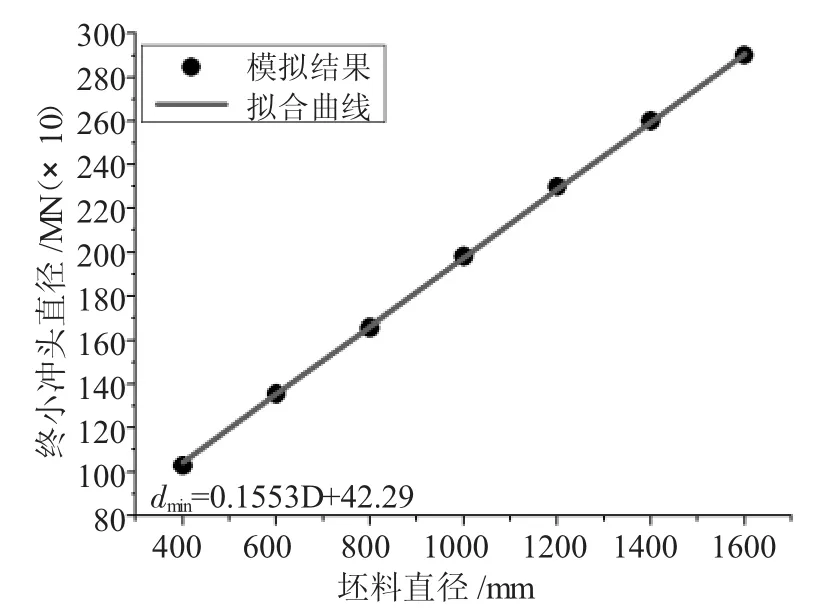
圖7 H/D=2.0最小沖頭直徑隨坯料直徑的變化關系

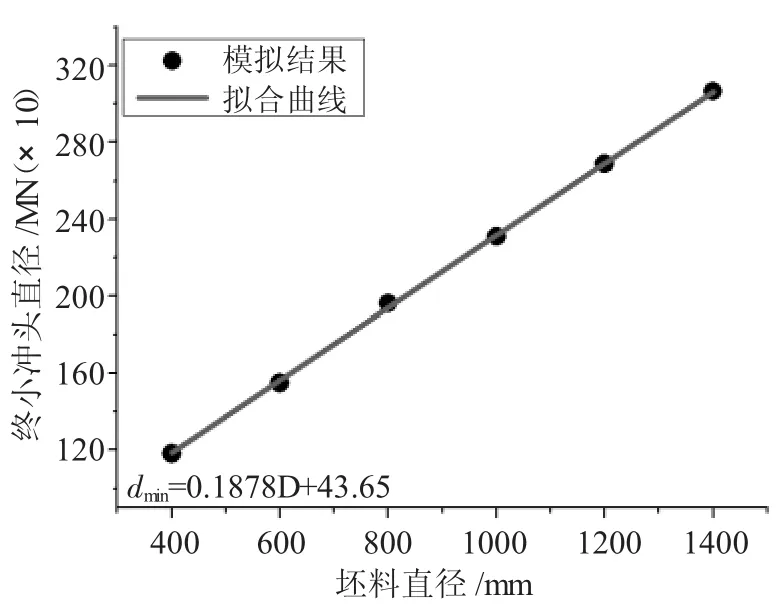
圖8 H/D=2.5最小沖頭直徑隨坯料直徑的變化關系

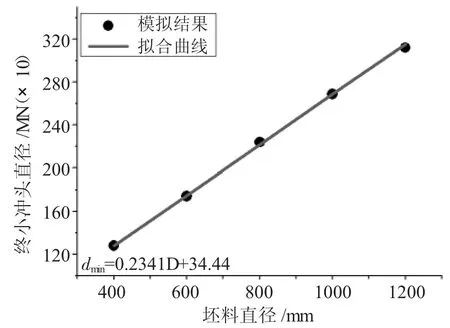
圖9 H/D=3.0最小沖頭直徑隨坯料直徑的變化關系

4 一定高徑比時圓柱鍛件沖孔最小沖頭直徑與坯料直徑參數化關系的建立

4.1 參數化的建立

根據圖5～圖9所示，在高徑比H/D在1.0～3.0之間，不同直徑坯料下的最小沖頭直徑隨著坯料直徑的增大而增大，并且呈線性增大關系。為了觀察最小沖頭直徑隨坯料直徑的變化關系在不同高徑比下的變化趨勢，將圖5～圖9匯總成圖10。

將不同高徑比下擬合曲線作參數化方程，如公式（3）～公式（7）所示。

在不同高徑比下，坯料的最小沖頭直徑與坯料直徑的變化關系不同。因此，在實際鍛件沖孔過程中，若坯料高徑比為 1.0、1.5、2.0、2.5、3.0 時，可以利用擬合公式（3）～公式（7），根據坯料直徑來計算最小沖頭直徑。

圖10 不同高徑比下最小沖頭直徑隨坯料直徑變化關系

同時針對高徑比在 1.0～1.5、1.5～2.0、2.0～2.5、2.5～3.0時，最小沖孔直徑與坯料直徑的關系可以在圖10中進行插值查表得出。

4.2 參數化驗證

為了驗證在高徑比為 1.0、1.5、2.0、2.5、3.0 時，圓柱鍛件直徑在400mm～1600mm的任意尺寸下，最小沖頭直徑與坯料直徑關系滿足參數方程（3）～（9）。選擇直徑為 500mm、700mm、900mm、1100mm、1300mm和1500mm的圓柱鍛件，高徑比分別為1.0、1.5、2.0、2.5、3.0尺寸的坯料進行沖孔模擬實驗，尺寸數據如表8。按照上文沖孔方案進行沖孔模擬實驗。

將沖孔模擬獲得圓柱鍛件沖孔尺寸和參數方程得到的尺寸對比，得到表9～表13。其中：

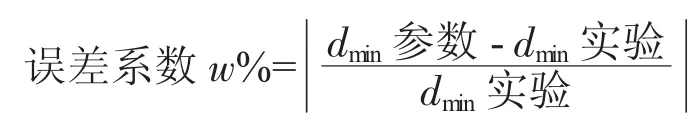
由表9～表13可知，針對參數化表達式的驗證，表8中各尺寸圓柱鍛件沖孔模擬實驗中獲得的極限尺寸與參數化表達式獲得的相應尺寸下的尺寸數據之間誤差系數w%＜3.0%。證明圓柱鍛件沖孔尺寸下限的參數化具有一定的可信性。

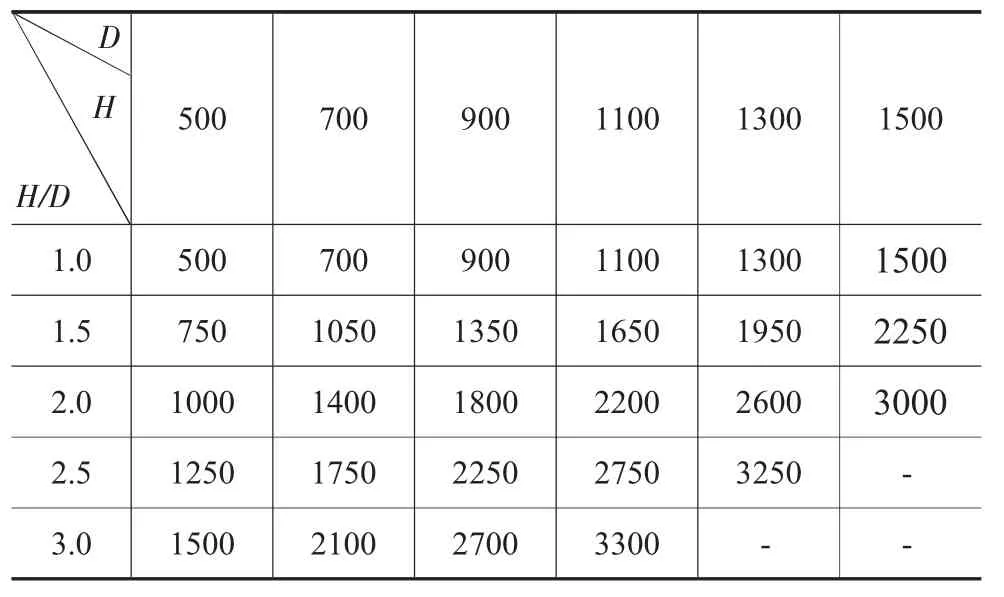
表8 圓柱鍛件尺寸/mm

5 結論

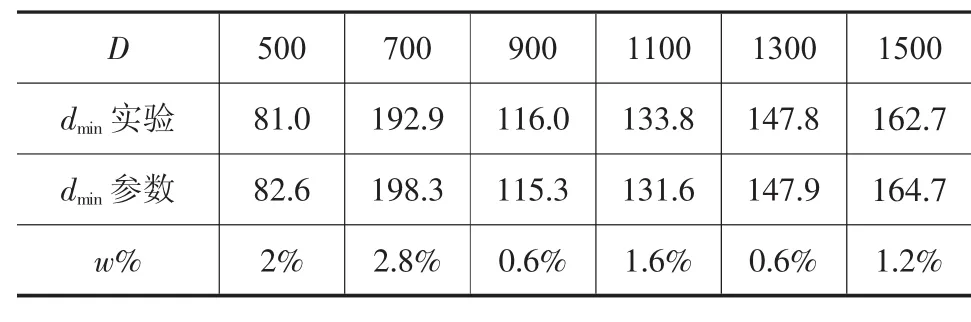
表9 H/D=1.0尺寸對比/mm

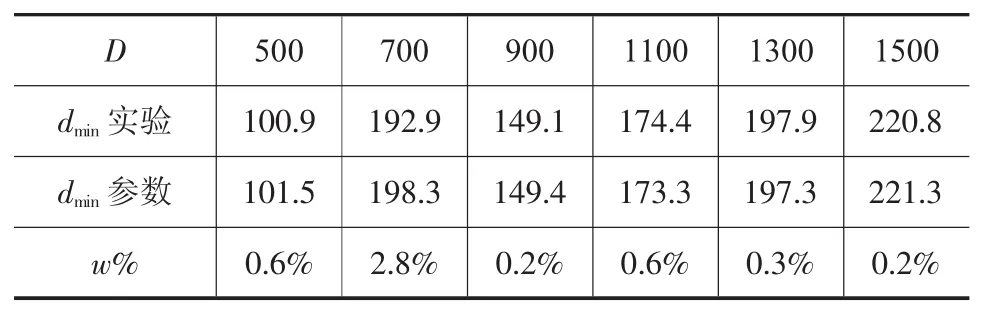
表10 H/D=1.5尺寸對比/mm

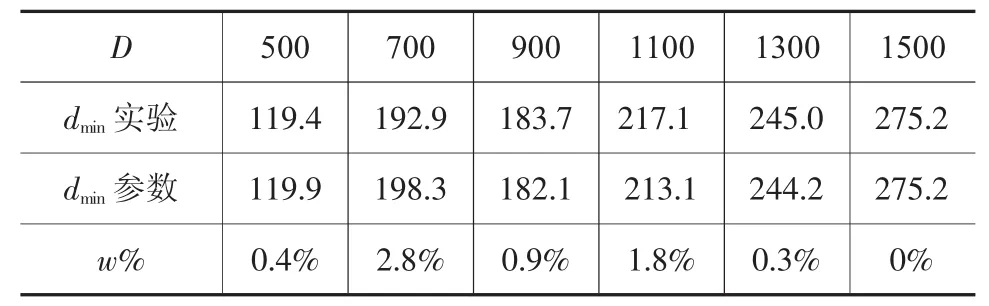
表11 H/D=2.0尺寸對比/mm

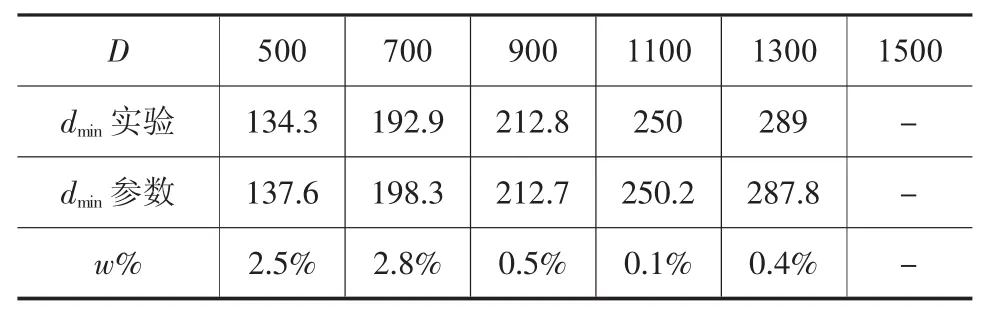
表12 H/D=2.5尺寸對比/mm

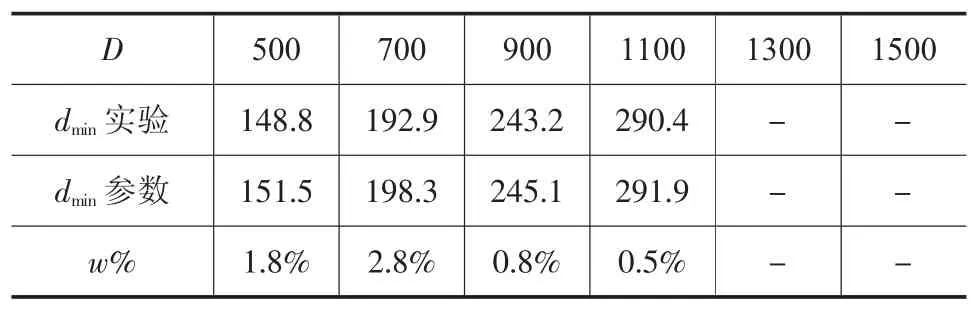
表13 H/D=3.0尺寸對比/mm

本文選取高徑比為 1.0、1.5、2.0、2.5、3.0 的圓柱鍛件，在不同圓柱鍛件直徑尺寸下進行沖孔工藝的模擬分析，得到以下結論：

在高徑比 H/D 為 1.0、1.5、2.0、2.5 和 3.0 時，不同直徑坯料下的最小沖孔直徑隨著坯料直徑的增大而增大，并且呈線性增大關系；

若坯料高徑比在1.0、1.5、2.0、2.5和 3.0時，可以利用參數化公式，通過坯料直徑來計算最小沖孔直徑；

當坯料高徑比 1.0～1.5、1.5～2.0、2.0～2.5、2.5～3.0時，最小沖孔直徑與坯料直徑的關系可以通過插值查表得出。