開口風洞聲陣列測量的剪切層修正方法

張 軍, 王勛年, 張俊龍, 盧翔宇, 陳正武

(1. 中國空氣動力研究與發展中心 氣動噪聲控制重點實驗室, 四川 綿陽 621000; 2. 中國空氣動力研究與發展中心 空氣動力學國家重點實驗室, 四川 綿陽 621000)

0 引 言

航空聲學風洞為飛機氣動噪聲研究提供了一種有效的試驗平臺。為準確評估大型客機機體噪聲指標和指導飛機的降噪研究，需要針對聲學風洞的特點發展一種有效的噪聲測試技術來精確測量機體噪聲源的分布[1-2]。聲學試驗過程中，通常將試驗模型放置在氣流內部，傳聲器陣列放置在氣流外部。這樣可以避免氣流與傳聲器相互作用產生的流致噪聲，但是聲波在到達傳聲器之前需要穿過射流剪切層。射流剪切層是一種非均勻介質，聲波在傳播過程中將受到反射、折射和散射等效應的影響，聲場特性會因此發生改變。因此，需要開展剪切層修正方法研究，對測量數據進行修正，才能獲得真實的聲源信息。

20世紀中后期，Miles[3]和Ribner[4]分別對聲波穿過具有相對運動速度的氣流的傳播效應進行了分析研究。Schlinker[5]和 Amiet[6-7]等人基于無限薄剪切層的假設，針對聲波穿過開口風洞剪切層產生的折射、散射等效應進行了理論分析和系統試驗研究，其剪切層修正方法被廣泛用于聲學風洞數據修正。Amiet推導的修正公式主要針對聲源位于射流中心線上、且與傳聲器在同一平面內的情況；而在測量過程中，并非所有傳聲器陣列的陣元都與目標聲源同平面。Candel[8]、Ahuja[9]等人也針對開口風洞剪切層對聲波的折射和散射效應進行了相關的理論和試驗研究工作。近年來，王毅剛[10]等人根據數值模擬和試驗測量結果，提出了一種基于有限厚度剪切層假設的聲漂移量修正模型。

本文主要研究剪切層折射效應引起的聲波相位失配修正，沒有考慮剪切層內湍流散射效應的影響。首先，通過湍流邊界層流場的Gortler理論解[11]給出風洞剪切層速度剖面，分析剪切層速度場的變化規律；其次，針對傳聲器陣列聲源定位的特點研究了4種剪切層修正方法，從計算精度方面對不同修正方法進行對比；最后，通過風洞實驗驗證理論方法的有效性。

1 波束形成算法

風洞噪聲源定位一般采用波束形成算法。傳聲器陣列數據處理時，首先根據各通道采集的時域聲壓數據生成互譜矩陣：先將每個通道的信號數據分塊平均(以減小背景噪聲的影響)，然后采用快速傅里葉變換將時域數據轉換為頻域數據。傳聲器陣列的互譜矩陣可以表示為：

(1)

其中，N為陣列傳聲器的數量，互譜矩陣G為Hermite型矩陣，Gmm′可表示為：

(2)

式中，K為傳聲器陣列數據分塊數，Pm′k(f)為第m′個傳聲器第k段數據塊的單邊頻域信號，Ws為頻譜分析的加窗幅值恢復系數。上標*號表示復共軛。互譜矩陣G的下三角元素與上三角元素復共軛相等。對于任意空間點，傳聲器陣列的聚焦向量定義為g=[g1,g2,…,gN]T，其中gn(n=1,2,…，N)為均勻流中單位強度單極子聲源的格林函數，即：

(3)

(4)

為了減小背景噪聲的影響，通常將互譜矩陣的對角線元素置零。根據式(4)就可以得到試驗模型的噪聲源分布結果。

2 剪切層速度剖面

在剪切層修正的理論模型中，通常將剪切層近似為無限薄的渦流面[6-7]，即認為射流內部的流速為U，射流外部的流速為0。但實際上剪切層具有一定的厚度，并且剪切層內的射流速度呈一定規律分布。從定常旋渦粘滯模型和湍流邊界層方程出發，Gortler[11]得到了2種不同速度的射流邊界的流場理論解。當其中一種射流的速度為0時，這種邊界即為風洞自由射流剪切層。因此，Gortler的理論解可推廣到風洞剪切層速度剖面的求解。引入自相似參數：

(5)

其中，x0、y0為風洞噴口端面上的參考點，σ是由風洞試驗確定的常數。經過推導，可以得到剪切層內的軸向和切向速度剖面表達式：

(6)

式中，U0為平均流速，U為軸向速度，V為切向速度，erf為誤差函數。一般來說，自由射流剪切層的半速度剖面位置與風洞的噴口邊緣線并不重合，式(6)中需設置一個偏移量ξ0。在Gortler的理論中，剪切層厚度是這樣兩個點之間的距離：流體的速度在其中一個點上接近0，在另一個點上接近射流速度U0。為了使剪切層厚度計算不受邊界選擇的影響，引入動量厚度:

(7)

Candel[12]研究指出剪切層的厚度約等于4倍動量厚度，即δ≈4δm=0.17x。

3 剪切層修正方法

風洞剪切層修正方法主要分為兩類，即時域方法和頻域方法。基于LEE、Lilley方程、CAA等的計算方法為時域方法，其優點是精度高且不受聲波頻率的限制，缺點是計算速度慢。大型聲學風洞的試驗段尺寸通常在10m量級，從聲源位置到傳聲器位置的距離也達數米，時域方法受網格尺度和時間步長的限制耗時太長而不適用。Schinker[5]等人指出，當聲波波長超過風洞噴口尺寸時，使用頻域剪切層修正方法不會引入較大誤差。因此，本文主要研究頻域剪切層修正方法。

3.1 Amiet 2D方法

如圖1所示，開口風洞核心射流與周圍的靜止空氣之間存在無限薄的剪切層[6-7]。假設聲源位于射流中心線上，Θ′為聲波的初始發射角，Θm為測量角，Θ為對流角，Θ0為折射角。Rt表示風洞噴口的半寬，Rm為聲源-傳聲器之間的測量距離。在風洞核心射流和剪切層的共同作用下，實際聲線將按照“對流-折射”路徑傳播并達到傳聲器m處。

圖1 聲波穿過剪切層的折射效應示意圖

根據對流關系和Snell定律，Amiet[6-7]得到了如下的角度修正關系：

RmcosΘm=RtcotΘ+(RmsinΘm-Rt)cotΘ0

(8)

(9)

(10)

式(10)中，c0和ct分別為射流內部和外部的聲速，Ma=U/c0為來流馬赫數。式(8)～(10)可使用牛頓迭代法求解。根據圖上的幾何關系，可以計算聲波從聲源到傳聲器的傳播延遲時間：

(11)

需要注意的是，Amiet 2D方法是通過圓形風洞噴口導出的，對于方形噴口(例如CARDC FL-17風洞)，需要推導Amiet三維修正方法。

3.2 平均馬赫數法

Oerlemans[13]等人提出了一種剪切層修正的工程化近似方法：假設聲源、傳聲器都位于平均流場內，則氣流的平均馬赫數為：

(12)

其中，z1為剪切層到傳聲器的距離，z2為聲源到傳聲器的距離(見圖1)。根據對流關系確定漂移后的聲源位置，進而得到修正后的聲波傳播延遲時間。

(13)

(14)

3.3 簡化射線法

由數值模擬結果得到啟發，根據聲波傳播的惠更斯原理和費馬原理，張軍[14]等人提出了有限厚度剪切層的簡化射線法修正方法。基于簡化射線法的延遲時間計算示意圖如圖2所示。

圖2 基于簡化射線法的延遲時間計算示意圖

Fig.2Schematicofdelaytimecalculationbasedonsimplifiedraymethod

射流內部和外部的聲波傳播時間分別為：

(15)

其中，x0=(x0,y0,z0),z0=σ(x0,y0)/2為剪切層半厚度點位置。因此聲線從射流內的聲源位置到射流外的傳聲器位置的總傳播時間為t=t1+t2。t是聲線與剪切層交點(x0,y0)為自變量的二元函數。根據費馬原理，兩點之間聲線的傳播滿足最短路徑原則，聲源-傳聲器聲波傳播延遲時間的計算轉化為求解下式的最小值：

(16)

式(16)可通過最優化數值方法求解。

3.4 射線追蹤法

在高頻條件下，聲波的傳播可視為聲線的傳播，聲線是與波陣面垂直的射線。從射流內聲源到射流外傳聲器的傳播延遲時間可以通過追蹤聲線的軌跡進行計算。聲線的傳播由以下方程組控制：

(17)

(18)

式中，xp為聲線的空間位置，v0為式(6)確定的剪切層速度矢量，c表示聲速，s=σ為慢變矢量，σ為聲波的波陣面，Ω=1-v0·σ為自定義的中間變量。給定剪切層速度場和聲波的初始方向矢量n0，上式可以通過自適應步長的Runge-Kutta法求解。

4 風洞實驗

為驗證上述剪切層修正方法的正確性和適用范圍，在中國空氣動力研究與發展中心(CARDC)0.55m×0.40m聲學風洞中開展了實驗測量[15]。實驗內容分為：剪切層速度剖面測量、聲波傳播延遲時間測量和噪聲源定位測量。

利用總壓耙進行剪切層速度剖面測量。總壓耙上有30根總壓管、1根靜壓管。總壓管通過測壓軟管連接DSM3200掃描閥，掃描閥的量程為1Psi。通過燕尾槽連接方式將總壓耙安裝在可移動的導軌上。

聲波傳播延遲時間測量使用射流內參考聲源和射流外傳聲器對。射流內參考聲源由發聲部件和整流罩組成，聲源發聲部件為功率5W的揚聲器，帶有音量控制單元，揚聲器的發聲頻率為0.1～20kHz，信噪比大于85dB，失真度小于0.1%。整流罩一面開有5cm×3cm的窗口，表面采用穿孔金屬網覆蓋，在保證透聲的同時也可避免氣流的干擾。傳聲器對采用GRAS公司的1/2 英寸46AE傳聲器，由2個相距30cm的傳聲器組成傳聲器對，距離風洞軸線0.666m。傳聲器對沿射流下游移測，移動間隔0.15m。對到達傳聲器的2個聲壓信號進行互相關運算可以確定延遲時間，進而確定聲波的傳播方向。

聲源定位測量采用射流內參考聲源和射流外傳聲器陣列。陣列傳聲器為GRAS公司的1/4英寸40PH傳聲器，陣列等效孔徑為0.72m，采用8條螺旋臂，每個螺旋臂上分布5個傳聲器，共計分布40個傳聲器。陣列面到聲源的距離為1.61m。剪切層修正實驗測量裝置如圖3所示。

圖3 剪切層修正實驗測量裝置[15]

4.1 剪切層速度剖面

圖4給出了30、50和70m/s風速條件下，風洞剪切層速度剖面實驗測量結果和理論計算結果的對比。圖中帶標記的彩色曲線表示測量結果，加粗的黑色實線表示理論計算結果，橫坐標ξ表示歸一化參數。D=0.55m，為風洞噴口寬度。x方向為射流方向，y方向在水平面內與x方向垂直。測量面為射流中心線所在的水平面。坐標原點選取如圖1所示。y=0為噴口壁面位置，y為正表示測點在靠近射流中心一側，y為負表示測點遠離射流中心。理論計算選取σ=9，ξ0=0.2。從圖中可以看出，剪切層速度剖面的測量結果和理論計算結果吻合較好。在不同流向位置處，由歸一化參數描述的剪切層速度剖面重合度較好，這說明剪切層的速度剖面具有“自相似”的特征，即在y/x相等的斜線上速度值大致相等。在高風速條件下，靠近風洞噴口(x/D=0.16)處的速度剖面分布在一定程度上偏離遠離風洞噴口處的結果，這說明剪切層速度剖面并不是嚴格的自相似。出現這種情況的原因主要有2個方面：一方面可能是由測量誤差導致；另一方面，出現偏差的測量剖面主要靠近噴口位置，在較高風速下風洞噴口附近的脫落渦對剪切層速度剖面可能有影響。

(b) U0=50m/s

(c) U0=70m/s

定義剪切層的厚度為兩點之間的距離，這兩點分別對應流速為核心射流速度的10%和90%的位置。圖5給出了剪切層厚度隨風速變化的測量結果和理論預測結果，其中灰色加粗實線是根據式(7)得出的計算結果，帶標記的實線表示測量結果。從測量結果可以看出，剪切層厚度沿射流方向呈線性關系增長，射流速度對剪切層厚度的變化幾乎沒有影響。理論預測結果在變化趨勢上與實驗測量結果符合，但是在斜率上有較大差別。根據一次曲線擬合，0.55m×0.40m聲學風洞剪切層厚度與流向位置之間的關系為：y=0.15x，x為距離噴口的流向距離。

4.2 聲波傳播延遲時間

圖6給出了從聲源到遠場傳聲器位置的聲波傳播延遲時間的實驗測量結果和理論計算結果對比。聲波頻率為8kHz，風速分別為30、50和70m/s。圓圈表示的離散點為實驗測量結果(通過互相關運算求出)，不同顏色和線型的曲線表示理論計算結果。可以看出，在不同風速下，理論結果和測量結果之間符合較好，不同理論方法之間的計算結果差別也很小。在不同的預測方法中，平均馬赫數法的計算速度最快，Amiet 2D方法次之，簡化射線法及射線追蹤法的計算速度較慢(由于使用了較為復雜的迭代算法)。

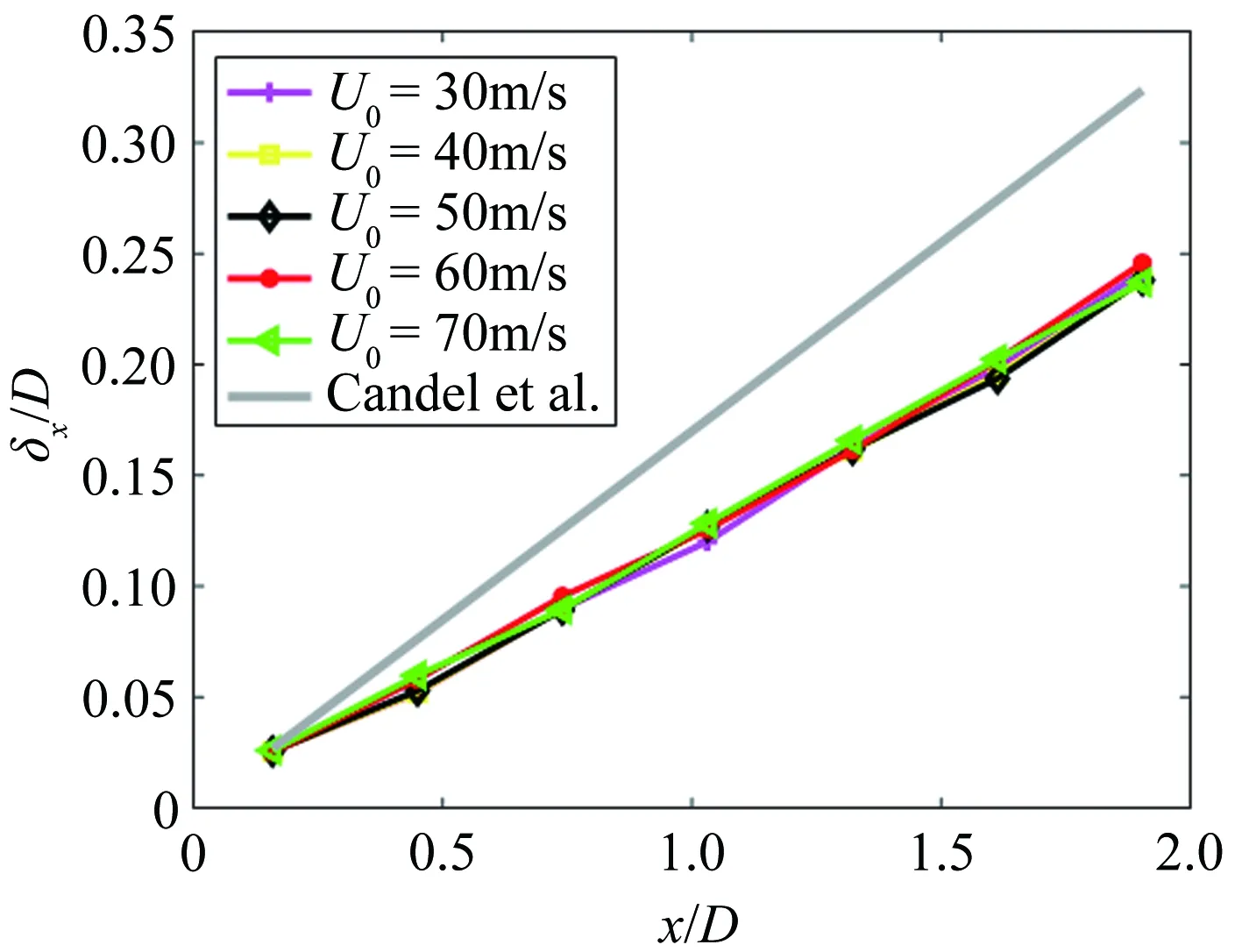
圖5 剪切層厚度的理論值和測量值對比

(a) U0=30m/s

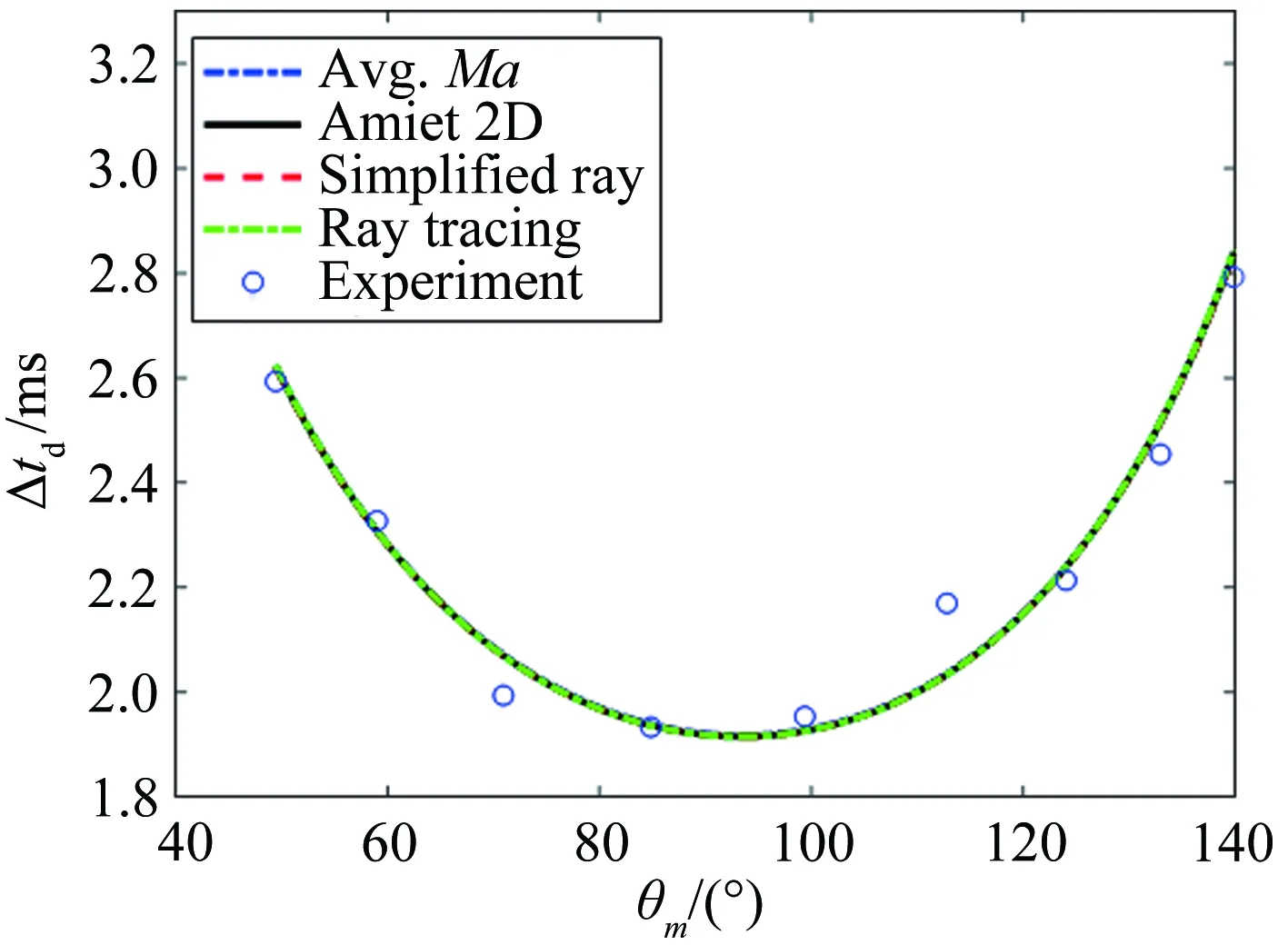
(b) U0=50m/s

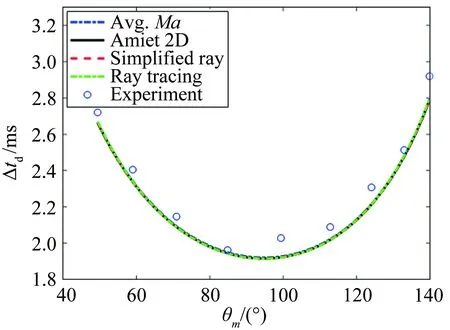
(c) U0=70m/s

根據不同方法得到的曲線幾乎重合，難以直觀地看出它們之間的差別。為考察不同剪切修正方法之間計算精度的差別，本文以Amiet 2D方法的計算結果為標準考察了不同修正方法給出的延遲時間相對誤差：

(19)

式中，ΔtAmiet表示Amiet 2D方法給出的計算結果，Δti(i=1, 2, 3)為其他修正方法的計算結果。

圖7給出了其他3種剪切層修正方法與Amiet 2D方法關于聲源到傳聲器之間的傳播延遲時間計算結結果的相對誤差。Error1～Error3分別表示平均馬赫數法、簡化射線法及射線追蹤法與Amiet 2D方法給出的結果之間的相對誤差。其中，射線追蹤法的計算沒有考慮剪切層厚度。根據計算結果，隨著來流馬赫數的增加(Ma>0.4)，平均馬赫數法與Amiet 2D方法之間的相對誤差增大。在測量角40°～140°范圍內，Ma<0.5的情況下，不同修正方法之間的相對誤差最大不超過5%。如果將馬赫數進一步限制在0.3以下(低速風洞常用馬赫數范圍)，簡化射線法、平均馬赫數法及射線追蹤法與Amiet 2D方法之間的相對誤差可以忽略不計(<1%)。如果僅對剪切層折射引起的相位失配進行修正，就計算速度而言平均馬赫數法最快。

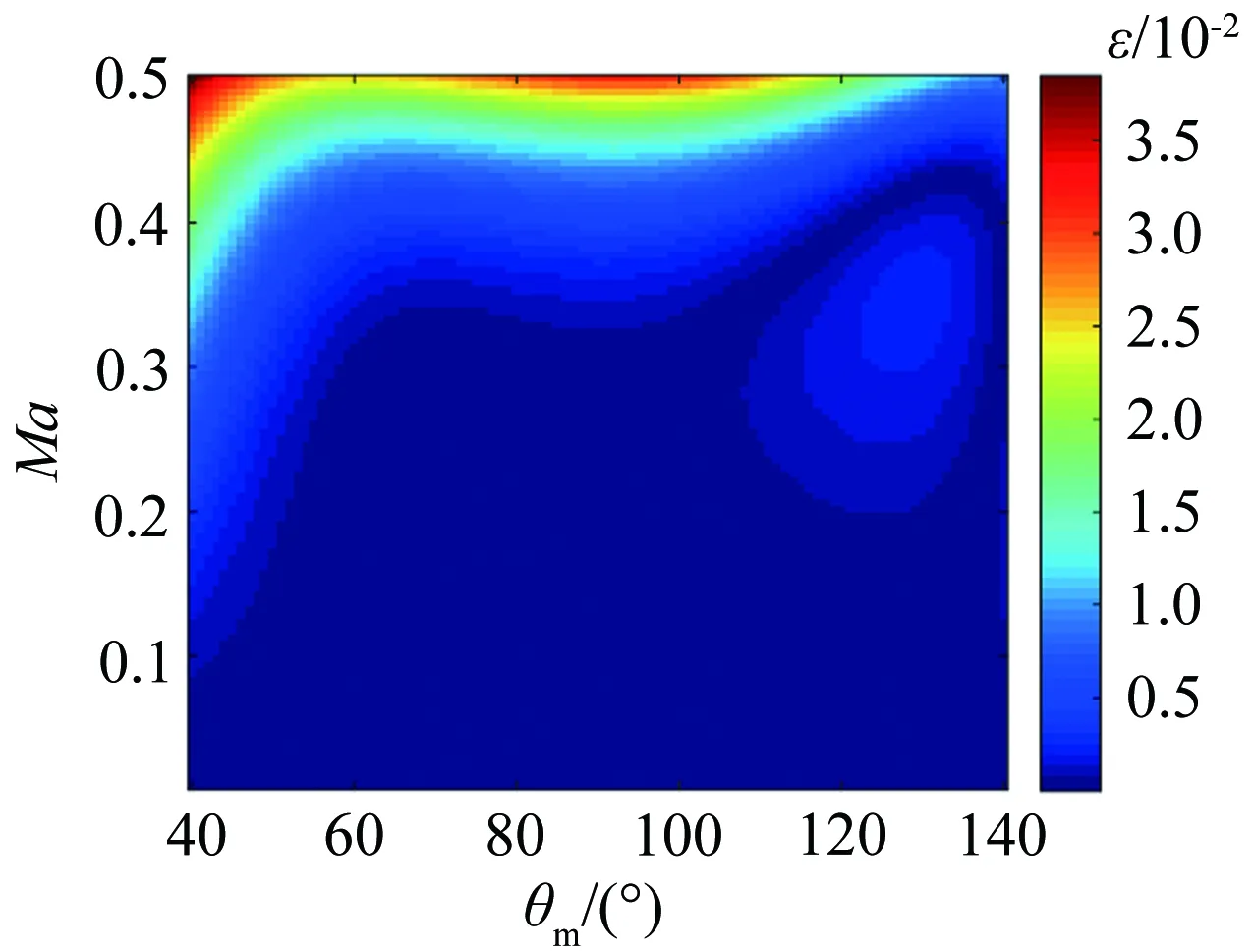
(a) Error1

(b) Error2

(c) Error3

4.3 聲源定位

表1給出了不同風速和頻率下，通過噪聲源圖得到的聲源位置漂移量計算結果，定義聲源位置漂移量在風速為0或不為0時的沿射流方向的聲源位置差。計算采用本文第1節的常規波束形成算法和第3節的剪切層修正方法。當風速為0m/s時，對應2、4和8kHz的揚聲器發聲頻率(與分析頻率相同)下噪聲源的空間位置為：(-0.16，0.18)，坐標軸為m。上述聲源位置是通過選取聲源圖中峰值點在掃描面上所處的位置得到的。表中N.C表示沒有經過修正的噪聲源x坐標位置，AMM、Amiet、SRM和RT分別表示經平均馬赫數法、Amiet 2D方法、簡化射線法和射線追蹤法修正后得到的漂移量。

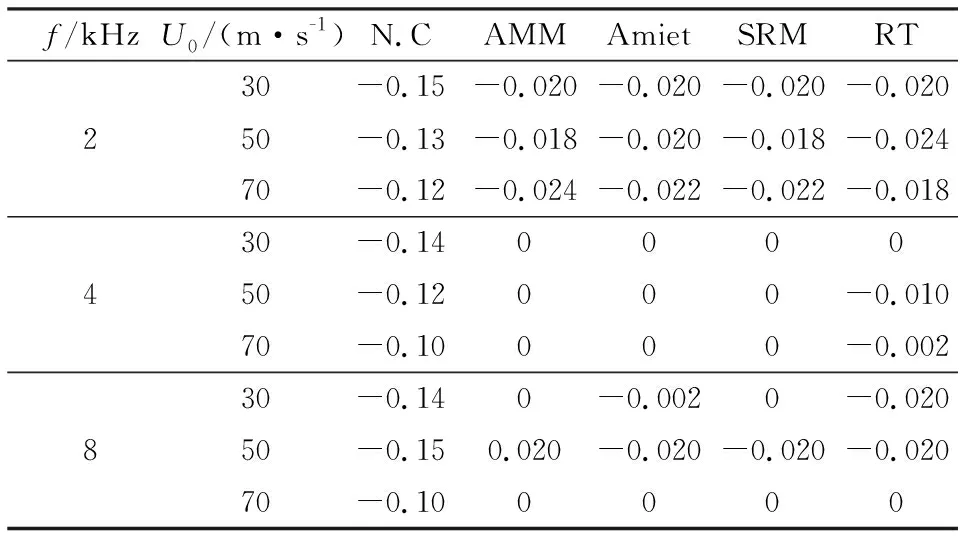
表1 不同修正方法計算得出的聲源位置漂移量(單位: m)Table 1 Source drift given by different shearlayer correction methods(unit: m)

從表中可以看出，在開口風洞實驗測量中如果不進行剪切層修正，那么從聲源圖得到的噪聲源位置相對真實聲源位置將出現漂移。且隨著風速的增加，聲源位置的漂移量增加(第3列數據)。在4kHz、8kHz分析頻率、相同風速條件下得到的漂移量大致相等，顯然這是符合物理實際的。2kHz條件下的修正效果比其他頻率下的更差，這是由傳聲器陣列的低頻分辨率問題導致的，采用CLEAN-SC等反卷積算法可改善這種情況。經過剪切層修正方法對延遲時間進行修正后，聲源的漂移量減小，噪聲源位置更接近真實聲源的位置。理想條件下，經過剪切層修正后聲源漂移量應當為0，但是實際上由于風洞背景噪聲、支撐裝置或風洞洞體結構對聲波的反射、陣列面上陣元位置誤差、傳聲器相位響應相對誤差等的存在，聲陣列成像得到的噪聲源位置與真實聲源位置總是存在一定的誤差。

5 射線追蹤法的快速計算方法

在射線追蹤法的計算過程中，要使從聲源處發出的射線準確到達測量點處，需要使用迭代算法，從而使得該方法的計算速度較慢。使用個人臺式電腦(4核i5-3470CPU 3.2GHz)在不開并行計算的前提下，追蹤一條聲線的時間約為1s。通常聲學風洞測量中的陣列高達上百個通道，掃描面網格點數上萬個，延遲時間計算需要追蹤上百萬條聲線，因此傳統的射線追蹤法無法適用于聲陣列在線測量。如果能夠大幅減少追蹤聲線的數量并能保證計算精度，那么射線追蹤法的計算速度就可以得到顯著提高。顯然，要減少追蹤聲線的數量，可以使用空間插值的方法，如圖8所示。

圖8 快速射線追蹤法的空間插值方法

理論上，聲線是從掃描網格點發出并穿過剪切層后到達傳聲器位置處的。根據線性聲學的互易原理，互換聲源和傳聲器的位置后，聲場的特性不會發生改變。讓聲線從傳聲器位置發出，穿過剪切層后到達掃描網格點位置，并根據射線軌跡計算這些網格點上的延遲時間，其余掃描網格點上的延遲時間通過空間插值方法進行計算。經過數值模擬，發現使用較少的聲線數量就可以達到較高的插值精度，這種方法可以將計算速度提高至少2個數量級。

6 結 論

在開口聲學風洞氣動噪聲試驗中，試驗模型和射流外傳聲器陣列之間存在剪切層。為了獲得真實的噪聲源位置，必須對陣列測量結果進行剪切層修正。本文首先在0.55m×0.40m聲學風洞中開展了剪切層修正的實驗研究，得到了不同風速下的剪切層速度剖面、聲波傳播延遲時間和聲源定位的結果。根據實驗結果，對剪切層速度剖面的Gortler理論解進行了驗證，并對比分析了4種剪切層修正方法。研究結果表明：

(1) 選擇自相似參數σ=9，ξ0=0.2時剪切層速度剖面測量值與理論值符合較好；剪切層厚度與軸向距離之間的關系為y=0.15x。

(2) 馬赫數Ma≤0.3，測量角θm在40°～140°范圍內，不同剪切層修正方法對聲波延遲時間計算結果的相對誤差在1%以內。不同修正方法均可以對對流-折射效應引起的聲源位置漂移進行有效修正。

(3) 提出了射線追蹤法的快速計算方法，該方法較常規射線追蹤法的計算速度可提高2個數量級，從而使其適用于聲陣列在線測量。

需要注意的是，本文所述的剪切層修正方法只考慮了由折射效應引起的聲波相位失配，沒有考慮陣列傳聲器處的幅值修正，因此，該方法主要應用于開口風洞中的噪聲源定位測量。對于遠場噪聲測量以及通過聲源圖(區域積分)估計目標區域的輻射聲功率等應用場合，則需要考慮剪切層的幅值修正。同時，本文也沒有考慮剪切層內的湍流散射效應對聲波傳播的影響，對于純音噪聲(例如螺旋槳、直升機旋翼氣動噪聲中的純音分量)的遠場測量，剪切層內的湍流將會使噪聲的頻譜特性發生改變(國外文獻稱之為“Spectral broadening”[17])。為了得到更加準確的射流內聲源信息，下一步需要繼續開展這些方面的研究工作。