用矩陣求圖中路徑數目的另一種證明方法

王 濤

（長沙民政職業技術學院通識教育中心，湖南長沙410004）

一、問題的提出

1、用鄰接矩陣表示有向圖

如有向圖D(圖1所示)。

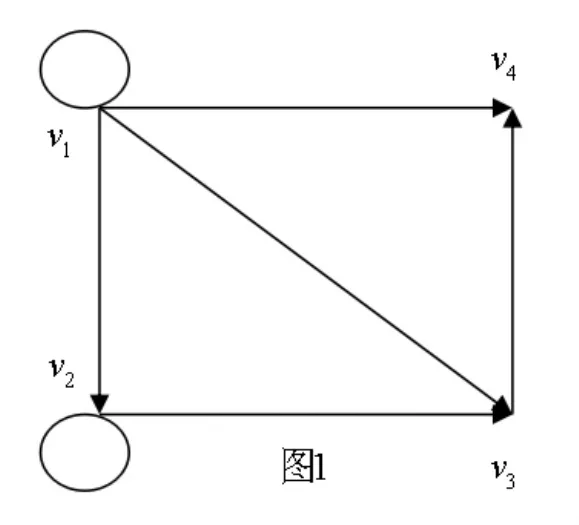
其A（D）（即圖1的鄰接矩陣）如下

此圖的行從左往右表示v1,v2,v3,v4,此圖的列從上往下表示v1,v2,v3,v4，矩陣中的元素aij

表示vi,鄰接到vj長度是1的路徑的條數（非負整數）

如v11（第一行，第一列）表示v1到v1長度為1的路徑的條數是1（一個環）

2、利用矩陣的乘法求D中長度為2的路徑數

如A2=A×A矩陣中元素aij表示vi鄰接到vj長度是2的路徑的條數（非負整數）

在結果矩陣中如v14=2（第一行，第四列）表示到v4長度為2的路徑的條數是2。

這個2是第一個矩陣的第一行與第二個矩陣的第四列對應元素相乘，然后相加所得

2=1 ×1 +1×0+1×1+1×0

從圖中可以觀察到這兩條路徑分別是

以此類推，因此我們可以得到定理；

矩陣AL中元素aij表示vi鄰接到vj長度是L的路徑的條數（非負整數）

接下來利用初等數學中的加法原理和乘法原理證明上述定理

二、定理的證明

如上的例子中v1到v4長度為2的路徑的條數可以理解為

這件事情可以分成四類方式，每類方式可以分成兩個步驟，分別是

第一類方式是v1→ v1→ v4，其中第一個步驟v1→ v1有1條路徑，第二個步驟v1→ v4有1條路徑，因此利用乘法原理可以得到第一類方式中共有路徑的條數是1×1。

第二類方式是v1→ v2→ v4，其中第一個步驟v1→ v2有1條路徑，第二個步驟v2→ v4有0條路徑，因此利用乘法原理可以得到第二類方式中共有路徑的條數是1×0。

第三類方式是v1→ v3→ v4，其中第一個步驟v1→ v3有1條路徑，第二個步驟v4→ v4有1條路徑，因此利用乘法原理可以得到第二類方式中共有路徑的條數是1×1。

第四類方式是v1→ v4→ v4，其中第一個步驟v1→ v4有1條路徑，第二個步驟v4→ v4有0條路徑，因此利用乘法原理可以得到第二類方式中共有路徑的條數是1×0。

所有最后用加法原理可得

1×1 +1 ×0+1×1+1×0=2

以此類推，可以證明

AL=AL-1A

矩陣AL中的元素aij表示vi鄰接vj到長度是L的路徑的條數（非負整數）。

三、結束語

本文利用了初等數學中的加法原理和乘法原理證明了離散數學中的一個很重要的定理，學生很容易理解。教材中有些重要定理的證明學生理解起來比較困難，教師要善于用簡單的、學生容易接受的方法去重新證明，從而達到最好效果。