基于ACO的超臨界給水系統模糊內模控制研究

毛求福， 馬永光， 彭 鋼

(1. 華北電力大學 控制與計算機工程學院，河北 保定 071003； 2. 國網河北電力科學研究院，河北 石家莊 050021)

0 引言

隨著我國電力行業的迅猛發展，火力發電機組承擔著主要用電量供應任務，如何保證火電機組穩定、安全、經濟高效的運行一直是電力行業研究的重點[1,2]。給水控制系統作為超臨界機組控制系統中的一個非常重要子系統，其控制任務是以中間點溫度或者焓值作為反饋校正信號，保證水/燃料比值恒定，然后控制蒸汽溫度，以滿足不同負荷下對給水流量的要求[3]。雖然常規的PID控制器結構簡單、穩定性較好、應用成本較低，在電廠中有著廣泛的應用，但是其要求被控對象有精確的模型，然而在實際運行中，由于給水控制系統的數學模型不僅具有較大的純遲延，而且其數學模型的參數會隨現場機組工況的改變而發生變化，因而對給水控制系統的設計，不僅要滿足跟蹤性能好，還要達到其對控制對象數學模型變化具有較強的自適應能力的要求，因而使得常規PID控制難以達到較為滿意的控制效果[4]。

近年來，隨著先進控制理論和智能優化控制算法的不斷深入研究，這些算法在超臨界機組給水控制系統中應用研究也逐漸發展起來，如自適應控制、模糊控制、預測控制等先進控制方法。文獻[5]提出了一種基于給水溫度前饋的給水系統模糊控制方法，改善了修正給水量控制方案的快速性，但未能保證在系統變工況下，仍具有較好的調節性能；文獻[6]采用了預整定自適應PID控制方法，具有結構簡單和魯棒性較好的特點，但對于系統模型較為依賴；文獻[7]采用了動態矩陣控制算法，改善了給水系統的控制品質，并有利于主蒸汽溫度的穩定，但對于參數的優化，辨識對象模型的精度有待改進。對此，本文采用結構簡單、調節參數較少、跟蹤調節性能好、魯棒性和抗擾動性強的內模控制算法構建超臨界機組給水控制系統的控制器，將內模控制器作為給水控制系統的外回路控制器，并運用不依賴于被控對象精確數學模型的模糊控制算法對控制器參數作進一步的調整，內回路控制器仍采用常規的PID控制器，從而結合三者構造出的模糊IMC-PID控制器，同時運用蟻群算法對控制器參數進行優化。此控制策略不僅改善了調節給水流量信號的大遲延特性，還提高了給水控制系統的魯棒性和抗擾動性。

1 直流鍋爐給水控制系統概況

目前，超臨界機組多采用的是直流鍋爐，不同于汽包鍋爐，雖然直流鍋爐的給水也經過加熱、蒸發和過熱3個階段，但各段之間未進行明顯的區分，其汽水流程示意圖如圖1所示。

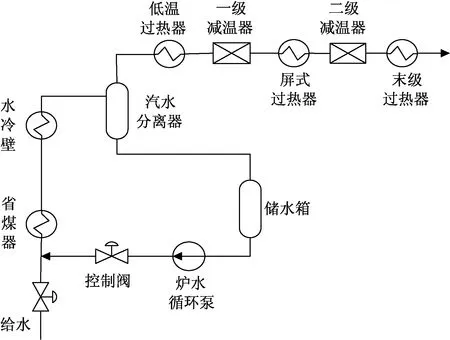
圖1 直流鍋爐汽水流程示意圖

在正常運行工況下，機組負荷一般不低于本生負荷(30%額定負荷)，基本處于直流運行階段,給水控制系統的主要任務是在不同負荷階段保證合適的燃水比，以控制過熱器出口溫度，實現過熱汽溫的粗調[8]。由于過熱汽溫對給水擾動有很大的延遲，難以保證過熱汽溫的調節品質，因而一般采用中間點溫度來反映水/燃料比[9]。為解決以中間點溫度作為校正水/燃料比值信號所存在的問題，提出采用在反映水/燃料比值的靈敏度和線性度方面具有更好品質的中間點焓值作為校正信號[10]。本文所研究的350 MW超臨界機組給水系統即采用中間點焓值作為水/燃料比值的校正信號，其簡化的結構原理圖如圖2所示。

圖2 采用焓值信號的給水控制方案

對圖2經過分析簡化后可得到基于中間點焓值的串級給水系統，其中外回路為中間點焓值控制回路，內回路為給水流量控制回路，其簡化的原理圖如圖3所示。

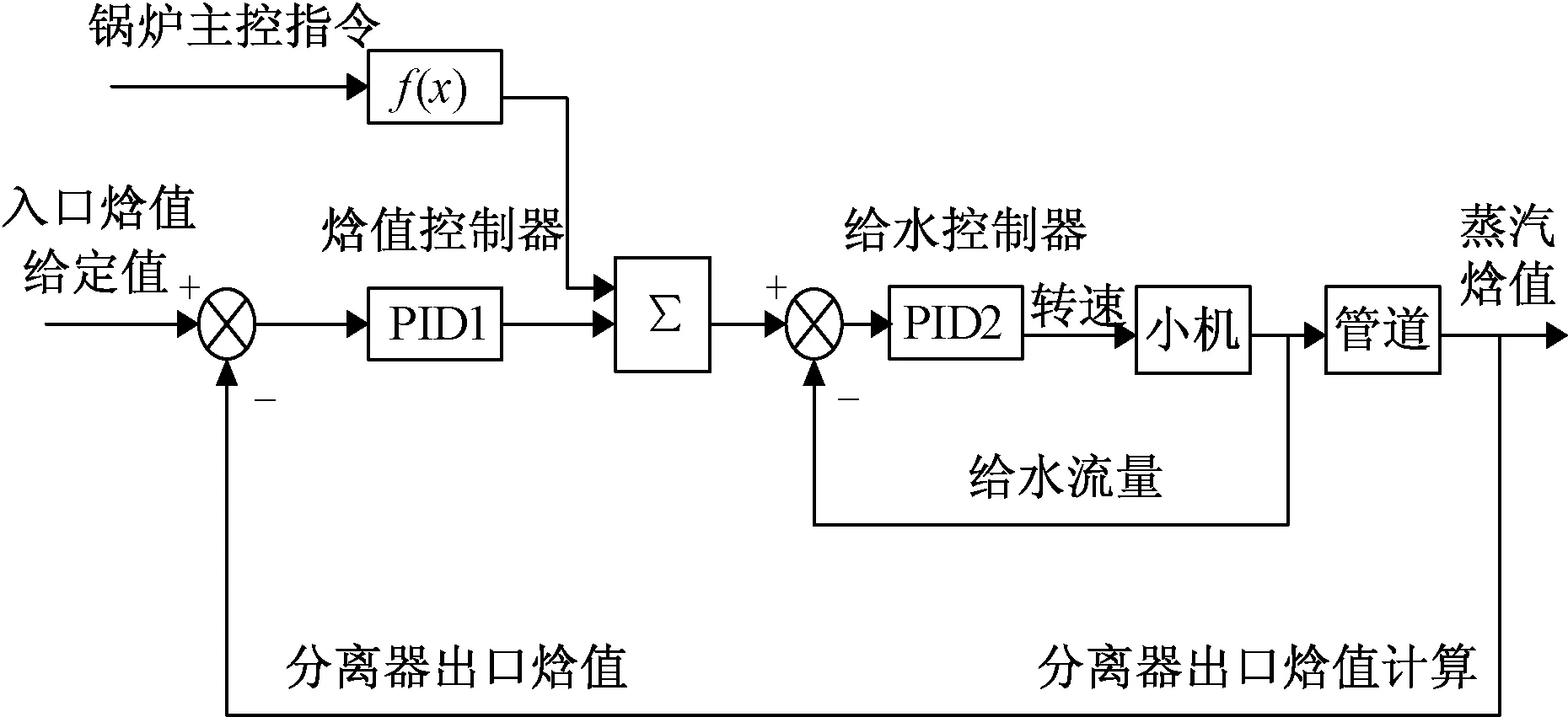
圖3 基于中間點焓值的串級給水系統原理圖

2 模糊內模控制算法原理分析

2.1 內模控制

內模控制是一種由Garcia和Morari首先提出的基于過程數學模型進行控制器設計的新型控制策略，具有結構設計簡單、調節參數少、能夠消除不可測干擾和魯棒性強等優點，在工業控制中得到廣泛的應用[11]，其基本結構如圖4所示。

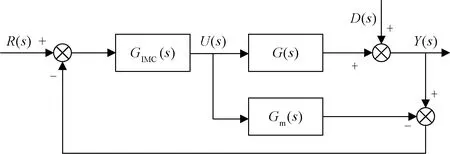
圖4 內模控制系統結構

圖4中，R(s)為系統輸入，GIMC(s)為內模控制器，G(s)為被控對象，Gm(s)為內部模型，D(s)為擾動輸入，Y(s)為控制系統輸出。由圖4可求得系統閉環響應的輸入輸出方程為：

(1)

由式(1)可知，若模型準確，即Gm(s)=G(s)，且GIMC(s)=1/Gm(s)，此時Y(s)=R(s)，也即內模控制器能夠使控制系統輸出完全跟蹤系統輸入。然而，在實際系統中，內部模型Gm(s)與被控對象G(s)總會存在一定的系統偏差，且內部模型Gm(s)的倒數中常常含有高階純微分環節以及純超前環節，這在物理上是不可實現的。因此，在實際的內模控制器中需要增加一個低通濾波器F(s)以滿足控制系統的穩定性和魯棒性。實際內模控制器的設計步驟為：

(1)穩定控制器設計

將內部模型Gm(s)分解為Gm+(s)和Gm-(s)兩項，即Gm(s)=Gm+(s)·Gm-(s)，且滿足Gm+(s)是內部模型中穩態增益為1的不可逆部分，Gm-(s)是內部模型中的最小相位部分。

(2)濾波器設計

為使控制器在物理上能實現，需要引入的低通濾波器為：

(2)

式中：Tf為濾波器時間常數；階次n一般取與內部模型階次相同。此時所得到的內模控制器為：

(3)

2.2 內模PID控制器設計

為把內模控制器轉化為PID控制器結構，將圖4進行等效變換為簡單反饋控制形式，如圖5所示。

圖5 內模控制等效變換結構

由圖5可得：

(4)

將式(2)、式(3)代入式(4)中可以得到：

(5)

選取典型的一階+純遲延系統作為給水控制系統的廣義被控對象的數學模型，即為：

(6)

此時，內模控制器的濾波器階數n=1，將式(6)中的純遲延環節e-τs用一階Pade逼近，即為：

(7)

將式(7)代入式(6)中可得：

(8)

依據穩定控制器的設計原則，可取

(9)

將式(8)、式(9)代入式(5)中可得：

(10)

由于理想PID控制器結構為：

(11)

將等效變換后的控制器Gc(s)轉化為常規PID控制器結構形式為：

(12)

對比式(11)與式(12)可得：

(13)

由式(13)可知，常規PID控制器的3個調節參數都僅與濾波器的時間常數Tf有關，因而在整定PID參數過程中僅需調節Tf即可。

2.3 模糊自適應PID控制器設計

模糊自適應PID控制結構原理圖如圖6所示。

圖6 模糊自整定PID控制系統結構

模糊自整定PID基本原理[12]：找出PID的3個參數Kp、Ki、Kd與系統偏差e和偏差變化率ec之間的模糊關系，在運行過程中不斷檢測e和ec的變化情況，根據制定好的模糊控制規則來對3個參數在線進行修正，以滿足不同e和ec時對控制參數的要求，從而使被控對象有很好的動態性能和靜態性能。

為保證模糊自整定PID控制律下的控制系統是全局穩定的，應該使用模糊整定規則調整Kp、Ki、Kd的偏差策略。依據工程技術人員的現場調試經驗，即根據不同負荷指令下給水控制系統的PID控制器參數，建立針對Kp、Ki、Kd3個參數的模糊整定規則如表1、表2、表3所示。

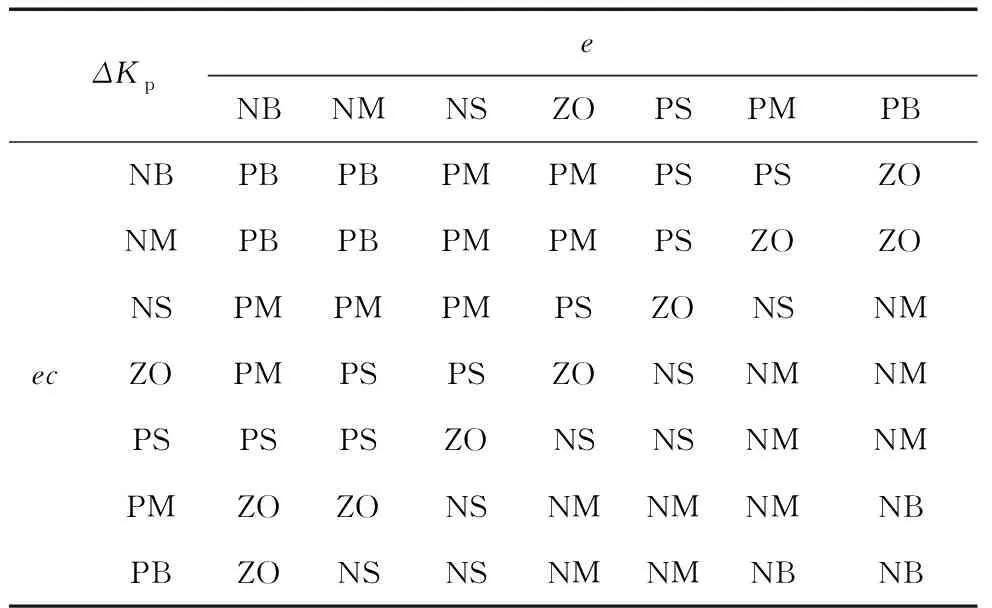
表1 Kp的模糊整定規則

表2 Ki的模糊整定規則

在實際應用中，首先根據被控對象的數學模型，初步確定一組PID參數Kp0、Ki0、Kd0，本文中結合內模控制器可以由式(13)計算出初始PID參數，再根據e和ec不斷計算PID控制器3個參數的修正量ΔKp、ΔKi、ΔKd，代入式(14)計算出PID的實際參數為

表3 Kd的模糊整定規則

(14)

模糊控制器采用兩輸入三輸出的形式，以e和ec作為輸入語言變量，ΔKp、ΔKi、ΔKd作為輸出語言變量。取輸入語言變量e和ec的等量級論域均為e,ec={-6,-4,-2,0,2,4,6}，輸出語言變量ΔKp、ΔKi、ΔKd的等量級論域分別為ΔKp={-0.6,-0.4,-0.2,0,0.2,0.4,0.6}，ΔKi={-0.06,-0.04,-0.02, 0,0.02,0.04,0.06}，ΔKd={-6,-4,-2,0,2,4,6}。輸入輸出語言變量的模糊量論域均取為“負大(NB)”、“負中(NM)”、“負小(NS)”、“零(ZO)”、“正小(PS)”、“正中(PM)”、“正大(PB)”7種。并且，e、ec、ΔKp、ΔKi、ΔKd語言變量的隸屬度函數均采用三角形的隸屬度函數曲線。

3 蟻群算法優化控制器參數

蟻群優化算法通過模擬自然界中螞蟻集體尋徑行為而提出的一種基于種群的啟發式隨機搜索算法[13]。其基本流程圖如圖7所示。

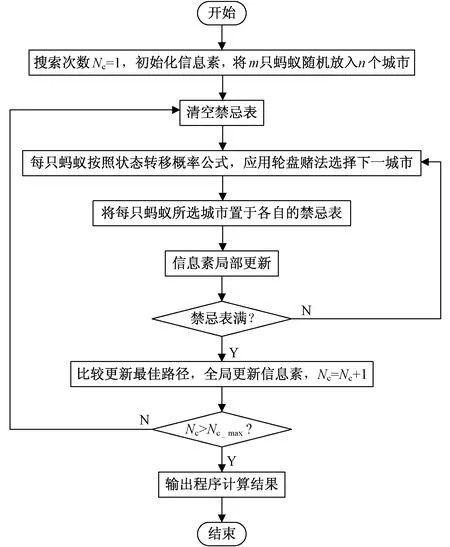
圖7 蟻群優化算法基本流程圖

鑒于該算法具有魯棒性強、并行性、自組織性、正反饋性以及易于與其他算法相結合等優點，本文提出所研究的模糊IMC-PID串級控制系統，運用蟻群優化算法對內模控制器的濾波器參數Tf和PID控制器參數都進行優化。

4 仿真研究

依據上述原理，所設計的模糊IMC-PID串級控制系統結構如圖8所示。

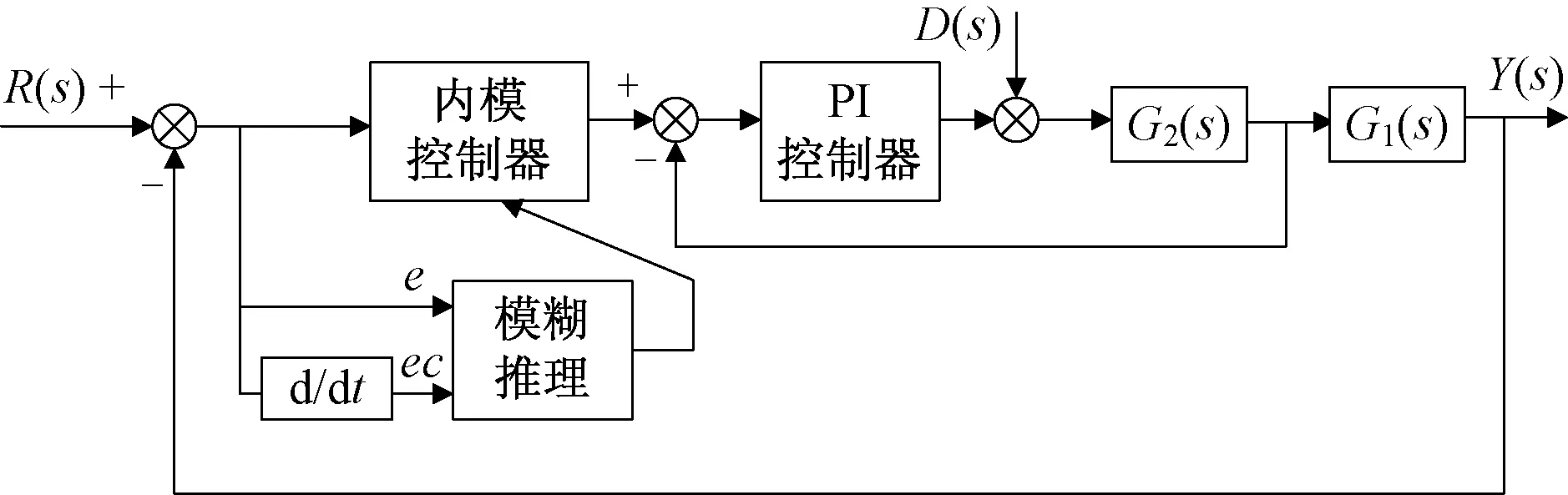
圖8 模糊IMC-PID串級控制系統結構

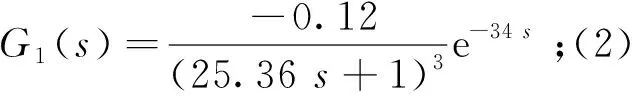
(1)給水系統的單位階躍擾動試驗

給水系統做單位階躍響應試驗，仿真時間為 2 000 s，仿真結果如圖9所示。

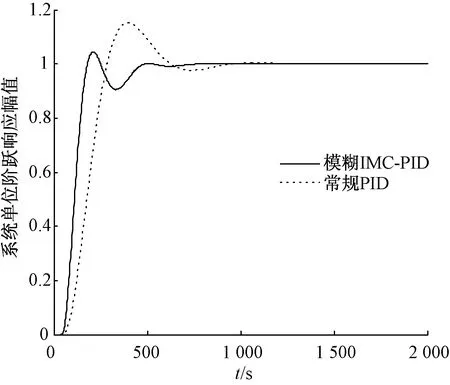
圖9 給水系統單位階躍響應曲線

由仿真結果可知，在給水系統單位階躍響應下，兩種控制方案的動態性能品質如表4所示。

表4 單位階躍擾動時動態性能品質對比

由表4可知，在系統單位階躍擾動下，采用常規PID控制方法時超調量和調節時間明顯比采用模糊IMC-PID控制方法時的要大得多，而其他調節品質幾乎差不多。綜合考慮，模糊IMC-PID控制效果明顯優于常規PID控制。

(2)給水系統的魯棒性試驗

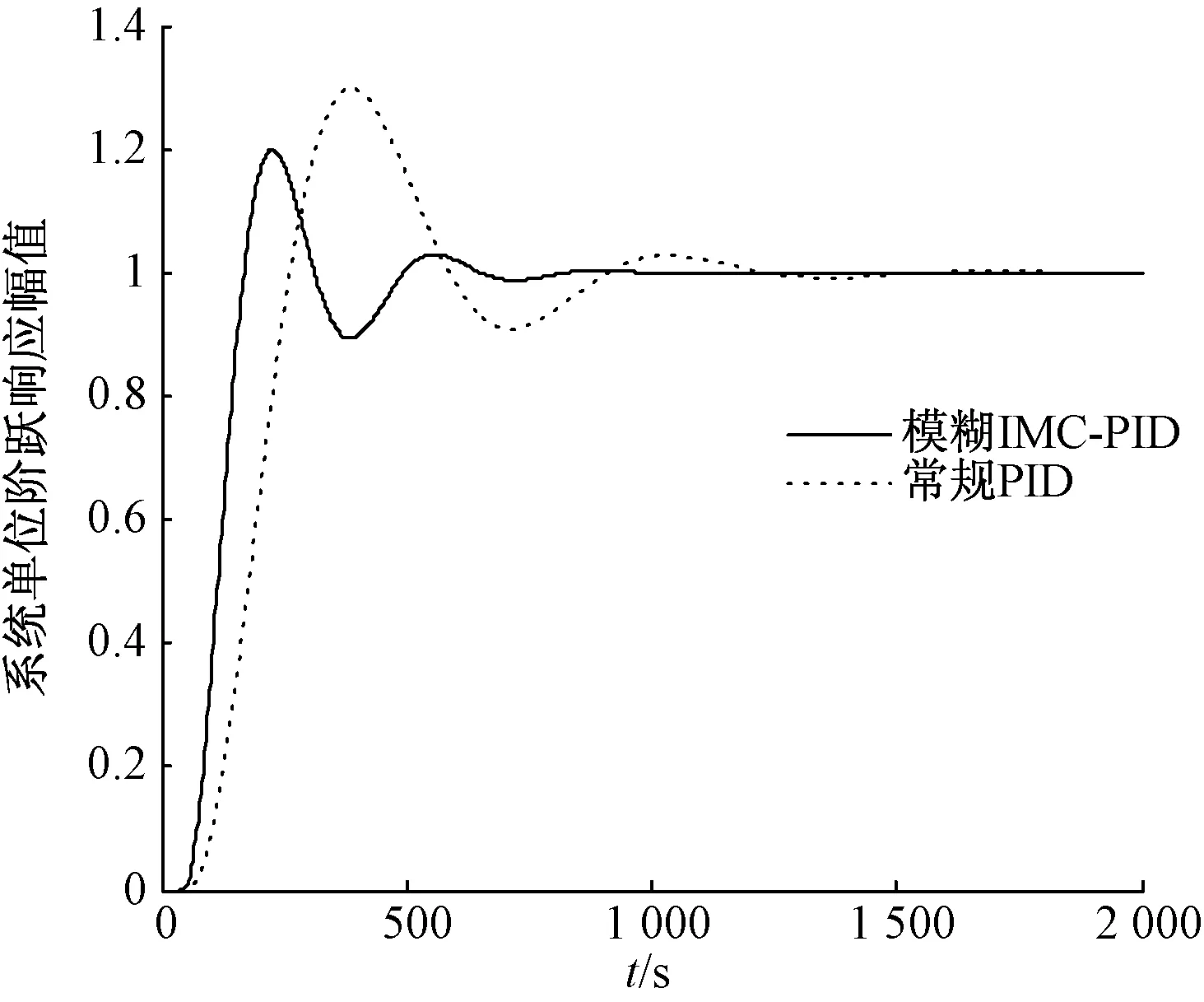
圖10 模型失配時系統單位階躍響應曲線

由仿真結果可知，在給水系統模型失配時的單位階躍響應下，兩種控制方案的動態性能品質如表5所示。

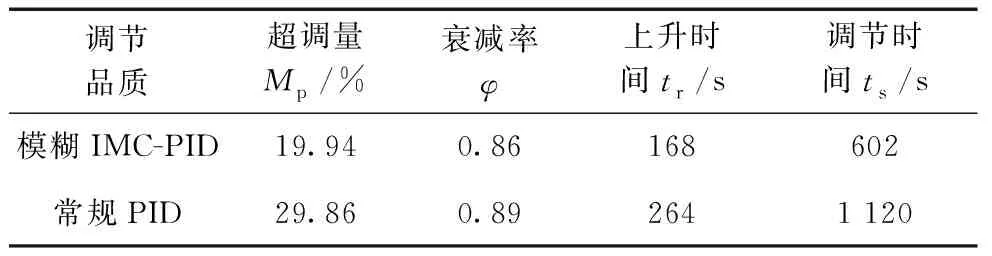
表5 模型失配時動態性能品質對比

由表5可知，鑒于給水系統復雜多變，系統模型會隨現場工況變化而發生變化，即當模型失配時，在系統單位階躍擾動下，采用常規PID控制方法時，超調量明顯增加，振蕩加劇，調節時間變長；而采用模糊IMC-PID控制方法時超調量和調節時間都變化較小，相比較而言，調節品質明顯比常規PID控制時要好，即采用模糊IMC-PID控制的魯棒性明顯優于常規PID控制。

(3)給水系統的抗擾動性試驗

對給水系統進行抗擾動性試驗，在給水系統單位階躍響應試驗中，當仿真運行到1 000 s時，在控制器與被控對象之間加入一定的擾動信號，同時系統做單位階躍響應試驗，仿真時間為2 000 s，仿真結果如圖11所示。

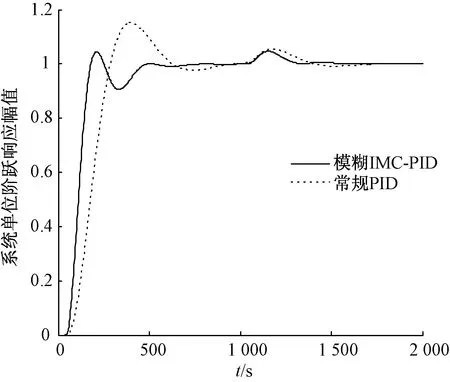
圖11 給水系統的抗擾動階躍響應曲線

由仿真結果可知，在控制器與被控對象之間加入階躍擾動信號時，兩種控制方案的動態性能品質如表6所示。

表6 加入擾動信號時動態性能品質對比

由表6可知，在控制器與被控對象之間加入階躍擾動信號后，由于系統存在大慣性、大遲延的特性，因而系統的超調量和調節時間會增大，但同采用常規PID控制方法相比較，采用模糊IMC-PID控制方法的擾動輸出信號消除時間和超調量均要小一些，從總體上來說，模糊IMC-PID控制的抗擾動能力要優于常規PID控制。

通過以上仿真試驗可知，本文針對給水控制系統數學模型所設計的模糊IMC-PID控制方案是可行的，能夠滿足所需的控制要求，并且在穩定性、魯棒性和抗擾動性方面都要優于常規PID控制方法。

5 結論

本文基于模糊和內模控制理論，針對超臨界機組給水系統具有大慣性、大遲延特性且對象參數隨工況變化較大等因素，設計了模糊IMC-PID串級控制系統，并將蟻群算法應用于控制器參數的優化。同時，以350 MW超臨界火電機組為例，進行了魯棒性和抗擾動性檢測仿真試驗。結果表明，模糊IMC-PID串級控制方法使系統超調量變小、調節時間縮短、穩定性提高，達到了很好的控制效果。且較常規PID串級控制方法有較強的抗擾動能力和更好的魯棒性。為進一步將先進的控制算法和優化參數的方法應用于實際電廠中提供了一定的借鑒意義。