結合故障輸出結構特征的極小沖突求解算法

徐旖旎 歐陽丹彤 劉 夢 張立明 張永剛

(吉林大學計算機科學與技術學院 長春 130012) (符號計算與知識工程教育部重點實驗室(吉林大學) 長春 130012) (jlxuyini@126.com)

基于模型診斷(model-based diagnosis)一直是人工智能領域中的重要研究方向，對人工智能領域的發展起到了至關重要的作用[1].模型診斷方法包括基于沖突的求診斷方法和直接求診斷方法.基于沖突的求診斷方法主要分為2個步驟:1)求出極小沖突集;2)求解極小沖突集的極小碰集，即為診斷解.直接求診斷方法就是利用SAT(satisfiability)求解器直接求出診斷解，而不需要產生極小沖突集[2].

在基于模型診斷問題中，求解極小沖突集是求診斷解的重要步驟之一.Reiter[3]最早采用沖突部件集的概念來計算極小診斷.早期許多專家使用定理證明器的方法求解極小沖突.Genesereth[4]提出用DART(device-independent diagnostic program)方法進行沖突識別.Haenni[5]在計算沖突集時使用歸結的方法.但傳統定理證明器效率較低，因此這些方法的實際應用并不廣泛.

國內學者也對沖突識別做出相關研究，如欒尚敏等人[6]提出利用系統結構信息求解極小沖突集的方法，方敏[7]提出先離線求沖突然后在線求極小沖突的方法.然而，這些算法效率較低且通用性差，因此沒有得到廣泛應用.20世紀90年代Hou[8]首次提出了利用枚舉樹求解極小沖突集的CS-Tree算法，但其算法由于剪枝策略會造成丟失解.2006年和2009年趙相福等人在CS-Tree，Inverse CS-Tree，CS-Tree with Mark Set[9]的基礎上分別提出2種改進算法CSSE-Tree[10]和CSISE-Tree[11],并首次使用SAT求解器求解沖突集，使得算法效率大大提高.劉伯文等人[12]在CSISE-Tree算法上進行改進，提出利用集合枚舉樹SE-Tree反向深度求沖突集的算法CSRDSE.CSISE-Tree算法主要針對非沖突集進行剪枝；而CSRDSE算法不僅對非沖突集進行剪枝，且根據沖突集的真超集一定不是極小沖突集的思想對某些能夠確定的非極小沖突集進行剪枝，減少了使用SAT求解器的次數，進一步提高了求解極小沖突集的效率.

本文在對CSRDSE算法分析的基礎上，提出結合故障輸出結構特征的極小沖突求解算法MCS-SFFO(computing minimal conflict sets based on the structural feature of fault output).在MCS-SFFO算法中提出非沖突集定理——故障輸出無關元件集的子集不是沖突集，即與異常輸出不相關的元件任意組合都不是沖突集.因此，對故障輸出無關元件的任意組合都不需調用SAT求解器進行判定.該算法在CSRDSE算法的基礎上進一步對集合枚舉樹進行無解空間的剪枝，從而減小SAT求解問題的規模.

1 預備知識

本節首先介紹基于模型診斷的相關定義和概念，然后介紹SAT問題的基本概念.

1.1 基于模型診斷

定義1. 診斷系統[3].診斷系統是可用三元組(SD，COMPS，OBS)表示，分別是系統描述、元件集、觀測集.

定義2. 基于一致性診斷[3].設Δ?COMPS，稱Δ為關于(SD，COMPS，OBS)的基于一致性診斷，如果SD∪OBS∪{AB(c)|c∈Δ}∪{AB(c)|c∈COMPSΔ}是一致的.

稱Δ為極小診斷當且僅當對于Δ的任一真子集Δ′，Δ′都不是一個基于一致性的診斷.

定義3. 沖突集[3].系統(SD，COMPS，OBS)的沖突集CS是一個元件集合{c1，c2，…，ck}?COMPS，使得SD∪OBS∪{AB(c1)，AB(c2),…,AB(ck) }不一致.

稱某個沖突集為極小沖突集，當且僅當該沖突集的任意真子集都不是沖突集[8].

1.2 SAT問題

我們用xi(i=1,2,…,n)表示布爾變量.xi或xi稱作文字，其中，xi稱作變量xi的正文字，xi稱作變量xi的負文字.X={x1,x2,…,xn}表示變量的集合.Qi(i=1,2,…,m)表示子句，每一個子句是一組文字的析取式.符號Φ代表CNF公式，CNF公式是由子句的合取構成，即合取范式CNF:Φ=Q1∧Q2∧…∧Qr，而SAT問題就是尋找是否存在一組X的賦值，使其滿足CNF公式.

定義4. SAT問題[13].SAT問題通常是指合取范式的可滿足問題.

2 利用SE-Tree反向深度求解沖突集算法

第1節介紹了沖突集的概念，根據沖突集的定義可以得到2個結論：

推論1. 當元件集C是沖突集時，C的任意嚴格超集都是非極小沖突集[12].

推論2. 當元件集C不是沖突集時，C的任意真子集都不是沖突集[12].

通過推論可知，對沖突集的所有嚴格超集以及非沖突集的所有真子集可不必再進行判斷.

本節介紹的SE-Tree反向深度求解沖突集算法就是運用了上述2個推論思想對集合枚舉樹進行剪枝，接下來介紹該算法的相關概念和算法思想.

2.1 相關概念

定義5. 集合枚舉樹[14].給定集合S，以樹結構形式按一定順序枚舉出S中元素的所有組合，稱這樣的樹為集合枚舉樹.

設節點N為枚舉樹中要遍歷的節點，下面介紹3條剪枝規則和標識規則.

剪枝規則1[12]. 當N是沖突集時，將N加入到沖突集合簇中.

若N是以其父節點為根節點的子樹上最左側分支上的節點，則跳轉至其父節點；否則，跳轉至以N的下一個兄弟節點為根的子樹的最左節點.

若N沒有下一個兄弟節點(此時N是葉節點)，則跳轉到下一個葉節點.

剪枝規則2[12]. 當N不是沖突集時，將N加入到非沖突集合簇中.

若N是經過下面節點回溯到的節點，則跳轉至N的最左側子節點的下一個兄弟節點為根節點的子樹的最左節點；否則，跳轉至其下一個兄弟節點.

若N沒有下一個兄弟節點(此時N是葉節點)，則跳轉到下一個葉節點.

剪枝規則3[12]. 當對N調用SAT求解器前，首先判斷N是否為非沖突集合簇中集合的子集.若是，按照剪枝規則2跳轉到下一個節點；否則，對N調用SAT求解器.

標示規則[12]. 當N是沖突集時，將N加入到沖突集合簇中，將其標示“0”，并將沖突集合簇中N的超集標示“1”.

2.2 CSRDSE算法

CSRDSE算法的主要思想就是基于剪枝規則和標識規則在反向遍歷集合枚舉樹時對樹進行剪枝.該算法偽代碼如下：

算法1. CSRDSE.

①Node=SE-Tree的最左節點；

② While (Node≠?)

③notCS=isunsolve(Node)；

④ If (notCS=0)

⑤judge←ISCS()；

⑥ If (judge=0)

⑦addtosolve(Node)；

⑧ 按照剪枝規則2給Node賦值；

⑨ Else

⑩addtosolve(Node)；

3 CSRDSE剪枝規則的改進

設節點Leaf是SE-Tree中的一個葉節點，下面介紹2個定義.

定義6. 同層兄弟節點.設節點F是SE-Tree的一個節點，若節點F與葉節點Leaf在集合枚舉樹中處于同層，且節點F是葉節點Leaf同層中相鄰的下個節點，則稱F為Leaf的同層兄弟節點.

如圖1中{c1,c2,c5}的同層兄弟節點是{c1,c3,c4}.

Fig. 1 SE-Tree of {c1,c2,c3,c4,c5}圖1 {c1,c2,c3,c4,c5}對應的集合枚舉樹

定義7. 子葉節點.設節點F是葉節點Leaf的同層兄弟節點，若Leaf與F之間存在葉節點，稱這些葉節點是Leaf的子葉節點.

如圖1中{c1,c2,c4,c5}的子葉節點是{c1,c2,c5}.

下面介紹算法CSRDSE中剪枝規則1的改進.

第2節我們提到，在算法CSRDSE剪枝規則2中，當葉節點不是沖突集時，跳轉至下一個葉節點進行判斷.例如圖1所示的SE-Tree中，當{c1,c3,c4,c5}不是沖突集時，需要跳轉至其子葉節點{c1,c3,c5}，{c1,c4,c5}，{c1,c5}進行判斷.但通過觀察可發現{c1,c3,c5}，{c1,c4,c5}，{c1,c5}都是{c1,c3,c4,c5}的子集，因此當{c1,c3,c4,c5}不是沖突集時，根據推論2可知，它的子葉節點也不是沖突集，因此可省去對{c1,c3,c4,c5}子葉節點的判斷，直接跳轉至{c2,c3,c4,c5}進行判斷.

設葉節點Leaf的所有子葉節點組成的集合為SUB_LEAVES.通過進一步觀察可知，在集合枚舉樹中，SUB_LEAVES中的所有元素都是葉節點Leaf的真子集.因此，當節點F不是沖突集時，SUB_LEAVES中的任一元素都不是沖突集，因此可省去對SUB_LEAVES中所有元素的判斷，直接跳轉至以葉節點Leaf的同層兄弟節點為根節點的最左節點進行判斷.

通過分析，剪枝規則1可改為：若N沒有下一個兄弟節點，則跳轉到以其同層兄弟節點為根節點的子樹的最左節點.

為方便闡述，本文將改進剪枝規則后的CSRDSE算法稱為CSRDSE 2.

在算法CSRDSE剪枝規則3中規定，在對某節點調用SAT求解器前，首先判斷其是否為非沖突集的子集.通過改進的剪枝規則2可知，當葉節點不是沖突集時，不必再判斷其子葉節點是否為非沖突集的子集，因此，可減少遍節點的次數，同時也減少了對非沖突集合簇的檢測次數.

對本節提出的改進策略的最壞情況和最好情況進行分析，結論如下：

1) 最壞情況.當SE-Tree的所有葉節點都是沖突集時，使用算法CSRDSE 2遍歷集合枚舉樹時并不能跳過葉節點的子葉節點，此時，算法CSRDSE 2與算法CSRDSE訪問節點次數相同，因此改進策略失效.

2) 最好情況.當SE-Tree的所有葉節點都不是沖突集時，使用算法CSRDSE 2在訪問完最左節點后算法結束，因此算法CSRDSE 2訪問節點的次數為1.而算法CSRDSE仍需遍歷全部葉節點，因此當系統元件總數為n時，算法CSRDSE訪問節點的次數是2n-1，為整棵枚舉樹節點總數的一半.此時，算法CSRDSE 2與算法CSRDSE相比，減少了對SE-Tree中一半節點的訪問，同時，還避免了2n-1-1次與非沖突集合簇的檢測.

4 結合故障輸出結構特征的極小沖突求解算法

CSRDSE 2算法優化了求解空間，但是進一步分析可知，與異常輸出端無關的電路元件間的任意組合都不是沖突集.因此，本節在CSRDSE 2算法基礎上，提出在SE-Tree中對這些與異常輸出無關的電路元件間的所有組合進行剪枝，進一步縮小了SAT求解問題的規模.下面給出結合故障輸出結構特征的極小沖突求解算法的相關概念和算法思想.

4.1 相關概念

定義8. 故障輸出元件.對于三元組{SD,COMPS,OBS}，若存在元件c∈COMPS，c的輸出是診斷系統的輸出，且該輸出是系統的故障輸出，即該輸出的觀測值與預期不符，則稱元件c是該系統的故障輸出元件.

定義9. 故障輸出相關元件集.對于故障輸出元件c，稱從電路輸入到c的路徑上經過的元件(包含c)是故障輸出相關元件.系統中所有故障輸出相關元件組成的集合是系統的故障輸出相關元件集.

定義10. 故障輸出無關元件集.設集合S是系統的故障輸出相關元件集，稱集合COMPSS為系統的故障輸出無關元件集.

為了更好地理解相關定義，下面用C17電路來舉例說明.如圖2所示：

Fig. 2 C17 circuit圖2 C17電路

在C17電路中，假設輸出端12輸出異常、輸出端13輸出正常，則c4是故障輸出元件.故障輸出相關元件集為{c1，c2，c3，c4}，故障輸出無關元件集是{c5，c6}.

4.2 求解故障輸出無關元件集算法

算法2.GetCompS(SD.cnf，OBS.cnf).

① 初始化：outABCompS=?；

EXP_OUT=?；

onABCompS=?；

unOnABCompS=?；

COMPS，從SD.cnf的第1行中獲取；

OBS_IN，從OBS.cnf中獲取；

OBS_OUT，從OBS.cnf中獲取；

②EXP_OUT←getExp(SD.cnf，OBS_IN，COMPS)；

③ While (OBS_OUT中仍有未與EXP_OUT對比的元素)

④ If (OBS_OUT[i]≠EXP_OUT[i])

⑤outABCompS.add(輸出是

OBS_OUT[i]的故障輸出元件)；

⑥ EndIf

⑦ EndWhile

⑧ While(outABCompS中有未判斷的元素outComp)

⑨onABCompS.add(與outComp連接的元件)；

⑩ EndWhile

在算法2中，將系統描述、輸入觀測和系統所有元件正常表示的CNF形式輸入SAT求解器中，求出預期輸出EXP_OUT(行②)；將預期輸出與實際輸出對比，求出故障輸出元件集outABCompS(行③～⑦)；通過系統描述，求出故障輸出相關元件集onABCompS(行⑧～⑩)；最后求出故障輸出無關元件集unOnABCompS并返回(行～).

4.3 結合故障輸出結構特征的極小沖突求解算法

定理1. 非沖突集定理：系統的故障輸出無關元件集的子集不是沖突集.

證明. 反證法.設UNABCS是系統故障輸出無關元件集的任一子集.若UNABCS是沖突集，則根據定義3，當UNABCS中所有元件正常時系統的輸出與系統實際輸出不一致，即與UNABCS相關的所有輸出中至少有一個是系統的故障輸出.而根據定義10可知，與UNABCS相關的所有輸出是系統的正常輸出，故二者矛盾.因此，UNABCS不是沖突集.

證畢.

根據定理1我們可以進一步優化CSRDSE 2算法.在構造集合S的SE-Tree時，將故障輸出相關元件放在S的前半部分，故障輸出無關元件放在S的后半部分.例如，系統元件集為{c1,c2,c3,c4,c5},其中故障輸出相關元件集為{c2,c4}，故障輸出無關元件集為{c1,c3,c5}，其集合枚舉樹如圖3所示.

而通過觀察可知，樹中以{c1}，{c3}，{c5}為根節點的分支子樹中的所有節點恰好是故障輸出無關元件集{c1,c3,c5}的所有非空子集.因此，根據非沖突集定理，可將以{c1}，{c3}，{c5}為根節點的分支子樹剪枝，得到新的枚舉樹如圖4所示.

Fig. 3 SE-Tree圖3 集合枚舉樹

Fig. 4 SE-Tree after pruning圖4 剪枝后的集合枚舉樹

通過上述分析可知，在用CSRDSE 2算法遍歷SE-Tree的過程中，當遍歷到的節點是故障輸出無關元件集的子集時，便可終止遍歷這棵樹，因為剩余的所有節點都是故障輸出無關元件集的子集，不是沖突集.下面給出結合故障輸出結構特征的極小沖突求解算法MCS-SFFO.

算法3. MCS-SFFO算法.

輸入：系統描述的CNF文件SD.cnf、系統觀測的CNF文件OBS.cnf、故障輸出相關元件集onABCompS、故障輸出無關元件集unOnABCompS；

輸出：極小沖突集合簇MCSRes.

①CSRes=?，unCSRes=?，Node=?；

② 生成集合{onABCompS[0],onABCompS[1],…,onABCompS[NUM1-1],unOnAB-CompS[0],unOnABCompS[1],…,unOnABCompS[NUM2-1]}的集合枚舉樹CSTree.其中，NUM1是onABCompS[]的元素個數，NUM2是unOnABCompS的元素個數；

③Node賦值為CSTree的最左節點；

④ While (Node≠?)

⑤ If (Node?unOnABCompS)

⑥ Break；

⑦ Else

⑧ If (Node是unCSRes元素的子集)

⑨ 按照剪枝規則1給Node賦值；

⑩ Else

算法3按照故障輸出相關元件在前、故障輸出無關元件在后的順序生成集合枚舉樹CSTree(行②)，并將CSTree的最左節點賦值給Node(行③).每次迭代節點Node時先判斷Node是否為故障輸出無關元件集的子集(行⑤)，若是則跳出循環(行⑥)；否則，繼續使用算法CSRDSE 2遍歷CSTree(行⑧～).當遍歷完CSTree后，將沖突集合簇中標識為“0”的沖突集加入到極小沖突集合簇MCSRes中(行～)，最后返回MCSRes.

根據算法3的描述可知，算法3是完備算法，因為集合枚舉樹將組件的所有組合都枚舉出來，所有的極小沖突集會在遍歷完這棵枚舉樹之后全部產生，不會發生丟解.

其次，MCS-SFFO算法將故障輸出相關元件放在待枚舉的集合的前部，故障輸出無關元件集放在后部，對故障輸出無關元件間所有組合進行剪枝，因此與CSRDSE 2算法相比，調用SAT求解器次數將會大量減少，求解效率也將會明顯提高.

算法3的復雜性分析：設系統元件總數為n，系統故障輸出無關元件個數為k，則使用MCS-SFFO算法剪枝的故障輸出無關元件集子集的節點個數為2k.因此當k越大時剪枝的節點數越多.下面對算法的最好情況和最壞情況進行分析：

1) 最壞情況.當k=0，即故障輸出無關元件個數為0，此時故障輸出無關元件集子集個數為0，因此與算法CSRDSE 2相比，使用算法MCS-SFFO剪枝的節點個數沒有增多，算法MCS-SFFO退化為算法CSRDSE 2.

2) 最好情況.當k=n-1，即故障輸出無關元件個數約等于元件總數時，此時故障輸出無關元件集子集個數為2k.算法MCS-SFFO剪枝步驟可分為2個，首先直接剪枝2k個故障輸出無關元件集的子集節點，此時剩余子樹的節點數也為2k；然后使用算法CSRDSE繼續對剩余子樹進行剪枝.而算法CSRDSE仍需遍歷節點數為2k+1的整棵集合枚舉樹，與算法MCS-SFFO相比，多遍歷了集合枚舉樹的一半節點.

5 實驗結果

本節實現了CSRDSE 2和MCS-SFFO算法，將這2種算法與劉伯文等人[12]提出的CSRDSE算法進行了比較并給出了實驗結果.實驗運行平臺如下：Dell Dimension C521，Ubuntu 12.04 LTS，GCC編譯器，AMD Athlon(tm) 64 X2 Dual Core Processor 3600+，1.90 GHz，3 GB RAM.算法調用的SAT求解器為Picosat.

為與CSRDSE算法對比，本文測試用例仍選用文獻[12]中的電路，包括電路C17，Fulladder_1，Fulladder_2，Fulladder_3，Fulladder_4，Fulladder_5，Polybox_5，Polybox_9.在實驗中，對每個電路給出大量觀測，然后分別用CSRDSE，CSRDSE 2，MCS-SFFO算法進行求解.用算法MCS-SFFO求解沖突集時，首先根據系統描述和系統觀測求出電路的故障輸出相關元件集和故障輸出無關元件集，并將其保存至相應文件內；然后將該文件作為MCS-SFFO算法的輸入參數來求解極小沖突集.

表1是分別用CSRDSE和CSRDSE 2算法求解極小沖突集時平均訪問節點的次數.其中，d表示算法CSRDSE與算法CSRDSE 2平均訪問節點數之差，p表示算法CSRDSE與算法CSRDSE 2平均訪問節點數之比.從表1可以看出，與CSRDSE算法相比，CSRDSE 2算法平均訪問節點次數明顯減少，并隨著電路規模的擴大，CSRDSE 2算法效率提高越明顯.CSRDSE 2算法減少了對某些節點的子葉節點查找非沖突集合簇的次數，同時避免了與非沖突集合簇進行子集檢測的問題，但調用SAT求解器次數與算法CSRDSE相等.

Table 1 Average Number of Access Nodes表1 平均訪問節點數

表2是分別用CSRDSE和MCS-SFFO算法求解極小沖突集時調用SAT求解器次數.其中，d表示算法CSRDSE與算法MCS-SFFO平均調用SAT求解器次數之差，p表示算法CSRDSE與算法MCS-SFFO平均調用SAT求解器次數之比.從表2中可以看出與CSRDSE算法相比，MCS-SFFO算法調用SAT求解器次數明顯減少.對于不同電路，MCS-SFFO算法優化程度不同.Fulladder_1電路平均提高0.06倍，而Fulladder_3電路平均提高3.48倍.這些都源于Fulladder_1與Fulladder_3電路特征的差異.Fulladder_1電路的故障輸出無關元件數占元件總數比例較小，因此使用MCS-SFFO算法剪枝的節點較少，效率提高不明顯;而Fulladder_3電路的故障輸出無關元件數占元件總數比例較大，使用MCS-SFFO算法剪枝的節點也相對較多，求解效率提高較大.

表3是MCS-SFFO，CSRDSE 2，CSRDSE算法求解極小沖突集的時間對比結果，其中最后一列表示CSRDSE與MCS-SFFO求解時間的加速比(其中因除數為0而無法運算加速比用空白表示).從表3中可以看出，CSRDSE 2算法與CSRDSE算法相比，求解時間減少，但效率提高并不明顯；而MCS-SFFO算法與CSRDSE 2算法相比，大部分電路的求解時間明顯減少.這源于MCS-SFFO與CSRDSE 2算法遍歷節點數相對CSRDSE算法雖然都有減少，但CSRDSE 2算法并沒有減少調用SAT求解器的次數，只減少了掃描非沖突集合簇的次數，而MCS-SFFO大量減少了調用SAT求解器的次數.而調用SAT求解器耗時較長，因此MCS-SFFO算法效率提高更加顯著.

Table 2 Average Number of SAT Call表2 平均調用SAT求解器次數

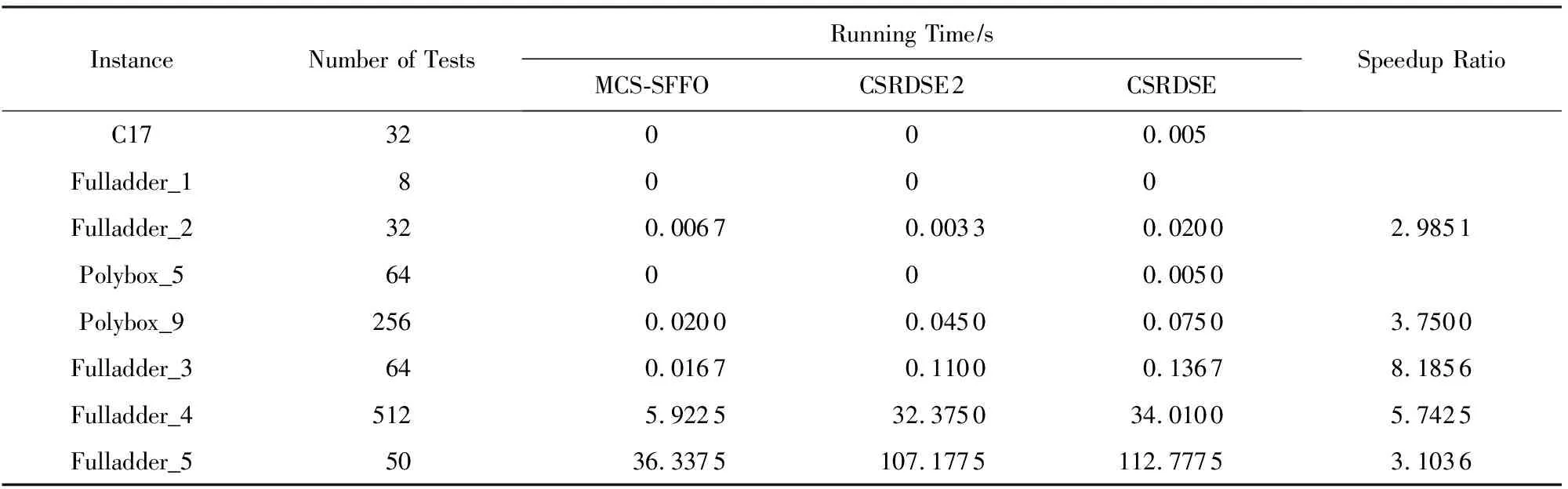
Table 3 Running Time表3 求解時間

6 結束語

基于模型診斷一直是人工智能領域內重要的研究方向.隨著SAT問題的求解算法不斷優化，使用SAT求解器求解沖突集已得到眾多學者的關注.本文在對CSRDSE算法研究的基礎上，提出了結合故障輸出結構特征的極小沖突求解算法MCS-SFFO.該算法首先對CSRDSE算法的剪枝規則做出改進，避免了對非沖突集的葉節點對應子葉節點的訪問；其次給出求解故障輸出無關元件集的算法GetCompS，根據系統描述和系統觀測，利用SAT求解器計算出故障輸出無關元件集；最后，提出非沖突集定理——系統故障輸出無關元件集的子集不是沖突集，根據此定理可對SE-Tree中的故障輸出無關元件集的子集節點進行剪枝，在生成SE-Tree時將故障輸出無關元件置于待枚舉集合末端，當遍歷到的節點是故障輸出無關元件集的子集時，停止遍歷SE-Tree.實驗結果表明，對CSRDSE算法的剪枝規則改進后，訪問節點數大幅度減少，求解時間相對較短.MCS-SFFO算法相對于CSRDSE算法剪枝節點數更多，調用SAT求解器次數明顯減少.并且，隨著電路規模的擴大，故障輸出無關元件數目也越多，因此，剪枝的節點個數也增多，MCS-SFFO算法效率提升更加顯著.