傳感網中UWB和IMU融合定位的性能評估

段世紅 姚 翠 徐 誠 何 杰

(北京科技大學計算機與通信工程學院 北京 100083) (材料領域知識工程北京市重點實驗室(北京科技大學) 北京 100083) (duansh@ustb.edu.cn)

無線傳感器網絡(wireless sensor network, WSN)由大量傳感器節點組成，是一種全新的信息獲取和處理技術，在現實生活中得到了越來越廣泛的應用，如軍事領域中實時監視戰場狀況、生態領域中環境監測和生物種群研究、工業領域中建筑物安全狀況的檢測等.其中的許多監測信息需要附帶相應的位置信息，因此傳感器網絡中節點位置信息的獲取至關重要.無線傳感器網絡最簡單的定位方法是為每個節點裝載全球定位系統(global positioning system, GPS)接收器[1]，用以確定節點位置.但是由于經濟因素、節點能量制約以及GPS對部署環境有一定條件的限制，導致這種方案的可行性較差.目前采用最多的定位方法是基于測距的方法[1]，比較主流的3種測量方法：1)基于時間的方法，包括基于信號到達時間(time-of-arrival, TOA)的方法[2-3]和基于信號到達時間差(time-difference-of-arrival, TDOA)的方法[4-5]；2)基于到達信號角度(angle-of-arrival, AOA)的方法[6-7]；3)基于接收信號強度(received signal strength, RSS)的方法[8-9].超寬帶(ultra-wideband, UWB)由于其準確的延遲分辨率，能夠提供精確的TOA到達時間估計，因此在傳感網定位系統中應用廣泛[10-11].然而，UWB測距方法容易受到多徑效應和節點間相對幾何位置關系的影響.近年來，慣性導航作為一種輔助定位方法能夠補償UWB的多徑效應和幾何拓撲問題，嵌入傳感器的慣性測量單元(inertial measurement units, IMU)如加速度計、陀螺儀、磁力計等能夠提供一系列連續的慣性信息，從而提高定位精度[12-13].本文提出了一種UWB和IMU融合定位方法，將UWB測距信息以及IMU的慣性信息融合起來，來定位傳感網中的目標節點.

在定位過程中，由于信號在傳輸過程中會受到噪聲、干擾、多路徑等隨機現象的影響，節點的位置估計會存在不確定性，從而影響定位精度.定位系統性能評估標準主要有幾何精度因子(geometric dilution of precision, GDOP)[14-15]、克拉美羅下限(Cramer-Rao lower bound,CRLB)[16-18]、后驗克拉美羅下限(posterior Cramer-Rao lower bound,PCRLB)[19-20]，其中CRLB比較常用.文獻[16]提出了基于CRLB的線性定位估計問題，給出了最小CRLB的推導過程；文獻[3,17]給出了UWB測距系統中基于TOA方法的位置估計誤差下限，得出在不存在多徑的理想情況下，CRLB與UWB脈沖寬度及信噪比(signal-to-noise ratio, SNR)有關；文獻[18]提出了在傳感網中一種基于半定理編程的節點定位算法，目標節點(target node, TN)的位置信息可以由錨節點(anchor node, AN)的位置信息及其他慣性信息(如加速度和方位角)來確定，并進一步導出了相應的CRLB.

然而CRLB僅僅關注空間狀態下相對位置間的關系對定位目標精度的影響，忽略了時間信息，如文獻[18]，不能滿足定位系統中對時間評估的要求.PCRLB考慮了時域信息[19-20]，可以作為定位系統性能的另一個評價標準；文獻[19]將基于無線電定位的位置估計、慣性傳感器測量和隨機游走模型結合起來，推導了用于慣性傳感器增強的移動定位的PCRLB；文獻[20]使用混合的射頻(radio frequency, RF)和圖像處理定位技術來定位膠囊內窺鏡檢查中的膠囊位置，以PCRLB作為性能評估的框架，實現了毫米級的定位精度.

基于以上分析，本文首先介紹了無線傳感網融合定位系統中狀態轉換和測量模型，然后推導了CRLB和PCRLB，最后進行了實驗仿真.實驗結果表明，本文提出的融合定位方法具有更好的時空定位性能，更能接近實際應用的理論精度下限.

1 無線傳感網融合定位系統建模

我們將UWB測距系統與慣性測量單元IMU結合，用來定位隨機移動模型中節點的位置.

令ck=(P,N)T=(xPk,yPk,xNk,yNk)T表示移動節點在狀態k時的狀態向量，其中k=1,2,…,K,K為總觀察數.(xPk,yPk)表示世界坐標空間中節點的2D坐標；(xNk,yNk)表示節點移動方向的標準向量.令zk表示移動節點在狀態k時的測量向量，則該系統的狀態方程和觀測方程被定義為

(1)

其中，qk表示過程誤差，即基于IMU慣性測量單元的誤差，服從協方差為Q的高斯分布；rk表示測量誤差，即UWB測距的誤差，服從協方差為R的高斯分布；矩陣Ak和矩陣Hk分別表示狀態轉移矩陣和測量關系矩陣，分別為

(2)

其中，dk表示基于IMU慣性測量單元測得的步長;

(3)

算法1. 傳感網融合定位系統中的卡爾曼濾波.

① 初始化z1,c1,P1,令c1=z1;

② fork=1,2,…,Kdo

④ 預測誤差協方差先驗估計:

⑤ 更新旋轉矩陣:R=RRkR-1;

⑥ 計算卡爾曼增益:

⑧ 更新誤差協方差后驗估計:

⑨ end for

2 性能評估

最初無線傳感網的定位性能由CRLB進行評估，其中的觀察結果彼此獨立，反映了空間狀態下相對位置間的關系對定位目標精度的影響.然而考慮到時域信息，觀察結果之間的獨立性不再存在，當前狀態移動節點的位置信息需要該節點在前一狀態的位置信息來判斷，即通過先驗信息得到后驗信息，因此引入了后驗CRLB，即PCRLB.

2.1 誤差分析

基于UWB和IMU的融合定位方法也會產生一定的誤差.基于UWB測距定位方法在測量目標節點與錨節點之間的距離時由于環境干擾等因素會造成測距誤差；基于IMU慣性器件(如加速度計、陀螺儀等)的定位方法在定位過程中會獲得一系列慣性信息如加速度、角速度等，將這些慣性信息進行姿態解算[21]可以獲得目標節點的步長信息以及角度信息，由于慣性信息本身存在誤差，因此獲得的步長信息以及角度信息也會存在誤差.由此我們可以得出，基于UWB和IMU的融合定位方法的誤差來源主要有：UWB的測距誤差以及IMU的步長誤差和角度誤差.

假設狀態k時目標節點TN的坐標為mk=(m1,k,m2,k)T；第n個錨節點AN的坐標為an=(a1,n,a2,n)T,n=1,2,…,N，其中N為錨節點的個數.目標節點的狀態轉移圖如圖1所示.假設目標節點的狀態信息矩陣為m=(m1,m2,…,mK)T，K為總的狀態數，對于狀態信息矩陣中的每一個元素可以得到：

mk=mk-1+dkwk+rk,

(4)

其中，dk為狀態k到狀態k+1時節點的移動步長，wk=(cosφk,sinφk)T表示節點的移動方向，rk表示由步長誤差和角度誤差造成的整體誤差.

Fig. 1 State transition of the target node圖1 目標節點的狀態轉移

基于IMU慣性測量單元測得的步長估計可以表示為

(5)

其中dk為實際步長：

(6)

基于IMU慣性測量單元測得的角度估計表示為

(7)

其中φk為實際角度：

(8)

除了基于IMU慣性測量單元獲得這些位置信息之外，我們還可以基于UWB測距方法測得目標節點與錨節點之間的距離估計:

(9)

其中sn,k為目標節點TN和第n個錨節點AN之間的實際距離：

(10)

2.2 空間性能評估：CRLB

(11)

其中J(mk)為費舍爾信息矩陣，在定義費舍爾信息矩陣之前，我們先定義聯合概率密度函數：

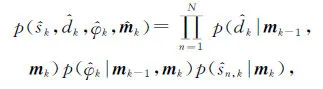
(12)

其中:

(13)

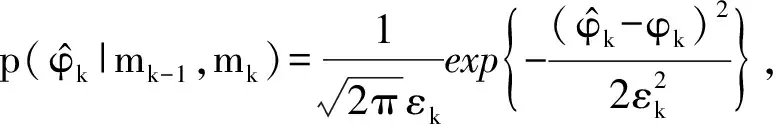
(14)

(15)

根據式(12)，我們可以得出費舍爾信息矩陣中的元素：

(16)

將式(12)～(15)帶入式(16)，可得費舍爾信息矩陣：

(17)

其中，

(18)

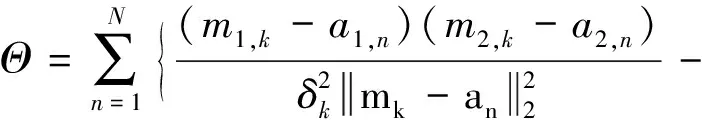
(19)

(20)

2.3 時間性能評估：PCRLB

如本節開頭所說，不考慮時域信息時，CRLB最常用于提供系統性能的理論下限.利用后驗信息如步長和角度，再加上時間信息，我們可以將CRLB擴展到PCRLB.在推導PCRLB之前，我們先定義聯合概率密度函數：

(21)

(22)

為了計算狀態k時的費舍爾信息矩陣，定義：

(23)

其中:

因此:

(24)

子矩陣Jk可以通過該矩陣的偽逆求得，即:

(25)

k+1狀態的聯合概率密度pk+1為

(26)

根據狀態k+1的聯合概率密度我們可以求出狀態k+1的費舍爾信息矩陣J(m0:k+1)：

(27)

(28)

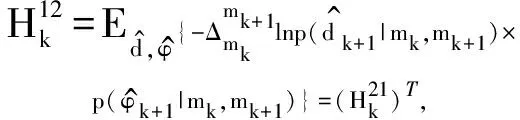
(29)

(30)

βk+1反映的是基于UWB測距的位置信息，即:

(31)

由J(m0:k+1)和Jk我們可以得到狀態k+1的費舍爾信息矩陣，即：

(32)

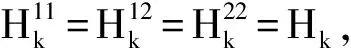
(33)

(34)

(35)

因此，后驗費舍爾信息矩陣：

Jk+1=βk+1+Hk-Hk(Jk+Hk)-1Hk,

(36)

進一步簡化可得：

(37)

其中，βk+1反映了基于UWB測距的信息，Hk反映了基于IMU慣性測量單元的信息.

3 實驗仿真與結果

本節我們用所提出的方法計算CRLB和PCRLB，來綜合評估UWB和IMU融合方法的時空定位性能.設計一個40 m×40 m的2D正方形傳感網環境，如圖2所示.區域中部署了4個錨節點AN，坐標分別是(10,10)，(10,30)，(30,10)，(30,30)，區域中間分散著其他的目標節點TN，其中*代表錨節點，○代表目標節點.我們假設錨節點的通信范圍可以覆蓋整個區域，目標節點可以從錨節點接收到所需要的信息.

Fig. 2 Deployment of nodes in sensor network圖2 傳感網中節點的部署圖

3.1 CRLB仿真

我們主要從3個角度來分析不同因素對CRLB的影響.

1) UWB+IMU融合方法和單獨采用UWB方法對CRLB的影響

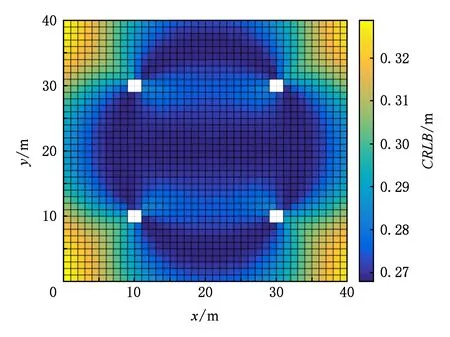
Fig. 3 CRLB based on the proposed hybrid method圖3 基于UWB+IMU融合方法的CRLB

2) UWB測距誤差和IMU步長誤差對CRLB的影響

Fig. 5 Average CRLB of different IMU step length error圖5 IMU步長誤差對平均CRLB的影響

3) 錨節點的部署結構和數目對CRLB的影響

我們還研究了錨節點在不同位置以及錨節點數量不同時對系統定位精度的影響.我們采用了4種錨節點部署方式，如圖7所示，其中*代表基站位置.按照不同的拓撲圖，計算相應的CRLB，如圖8～11所示.

Fig. 7 Different deployment of the anchor node圖7 錨節點的不同部署

Fig. 8 CRLB of Topology 1圖8 拓撲圖1對應的CRLB

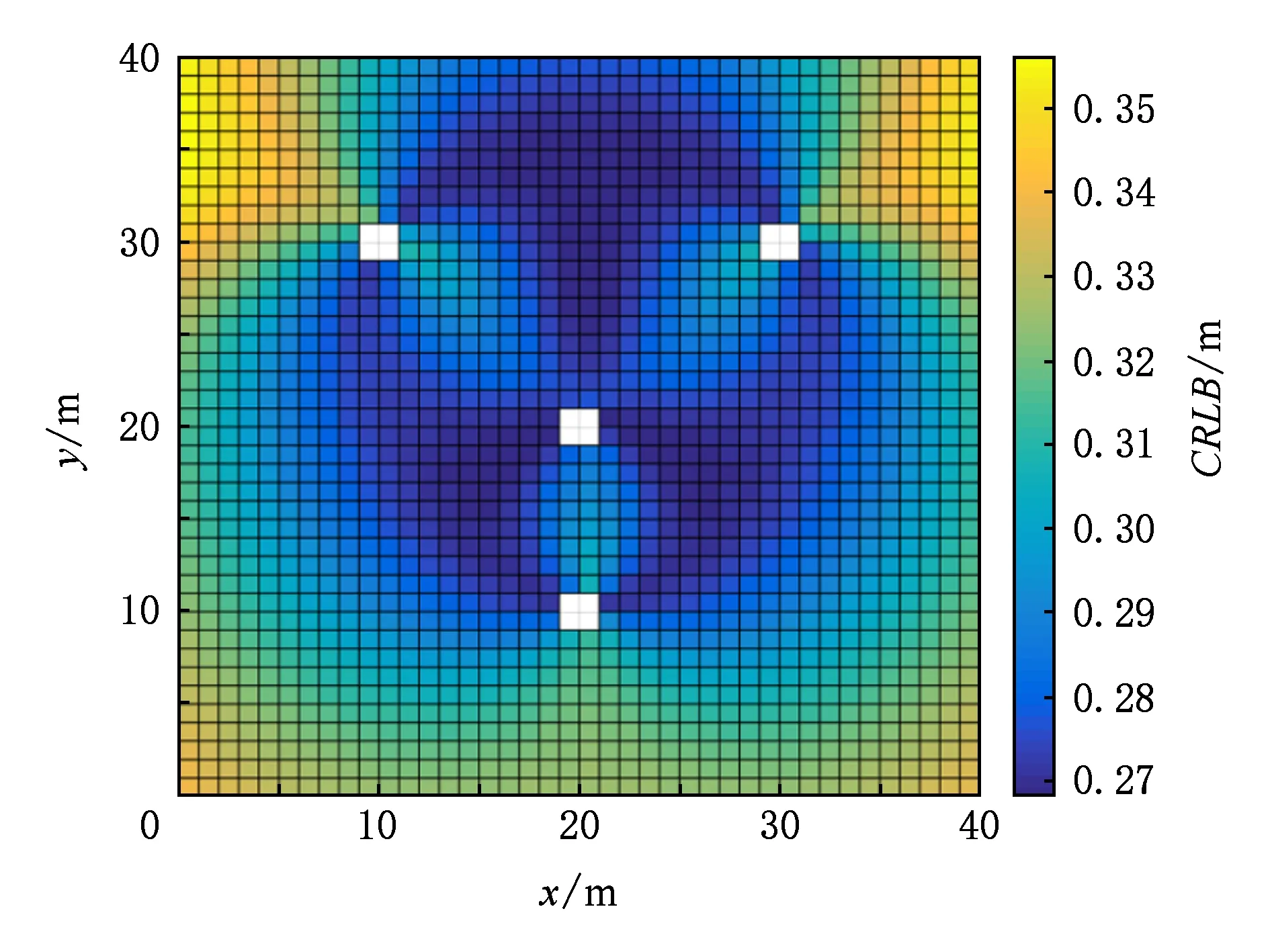
Fig. 9 CRLB of Topology 2圖9 拓撲圖2對應的CRLB

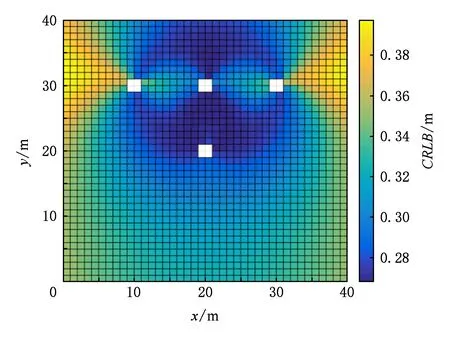
Fig. 10 CRLB of Topology 3圖10 拓撲圖3對應的CRLB

Fig. 11 CRLB of Topology 4圖11 拓撲圖4對應的CRLB

從圖8～11中可以看出：①當錨節點數目相同時，錨節點的部署形狀越接近于矩形，定位精度越高.如圖8所示，錨節點的部署形狀為正方形，最壞的CRLB=0.32 m，與圖9和圖10最壞的CRLB進行比較，精度分別提高了3 cm和5 cm.②圖10的CRLB最大，即表示定位精度最差，可能是由于錨節點部署的太密集而導致.③圖11的錨節點數目為6個，得到的最好CRLB=0.23 m，與圖8的最好CRLB相比，精度提高了4 cm.

3.2 PCRLB仿真

在計算PCRLB時，我們可以通過2.3節的公式遞歸地計算出費舍爾信息矩陣，由于式(28)～(30)中的方程表達式通常沒有近似解，為了解決這個問題，我們采用蒙特卡羅方法將連續積分轉換為離散求和，并最終計算出PCRLB.

從2個角度來分析不同因素對PCRLB的影響.

1) UWB+IMU融合方法中不同α和ε對PCRLB的影響以及單獨采用UWB方法和單獨采用IMU方法對PCRLB的影響

Fig. 12 PCRLB of the proposed hybrid method圖12 基于UWB+IMU融合方法的PCRLB

圖12顯示了在UWB+IMU融合方法中，在不同α和ε下可實現的最小誤差，我們還給出了單獨使用UWB方法(即沒有IMU慣性測量單元)以及單獨使用IMU方法(即沒有UWB測距定位)時可以實現的最小誤差.從圖12可以看出：①與基于單一UWB方法相比，基于UWB+IMU融合方法將IMU步長信息以及角度信息融合后，顯著提高了移動節點的定位精度.單獨使用UWB方法時，PCRLB=0.29m；采用融合方法后當α=0.05,ε=10°時，PCRLB=0.22m，定位精度為提高了7 cm.②與基于單一IMU方法相比，基于UWB+IMU融合方法將UWB測距信息融合后，補償了基于IMU方法所產生的累積誤差問題.③隨著α和ε的增加，PCRLB也增加，這意味著UWB+IMU融合方法的定位精度與步長及角度誤差成反比.④UWB+IMU融合方法的PCRLB在一定階段后會趨于穩定.

2) 不同錨節點部署結構對PCRLB的影響

按照圖7所示的不同拓撲圖，我們可以計算出相應的PCRLB，這里α=0.1,ε=10°，如圖13所示:

Fig. 13 PCRLB of different topologies圖13 不同拓撲結構產生的PCRLB

從圖13可以看出：①相同數目的錨節點但不同結構的拓撲，對定位精度會產生不同的影響，但影響較小，如拓撲圖1的PCRLB=0.235 m，拓撲圖2的PCRLB=0.24 m，拓撲3的PCRLB=0.245 m，波動范圍不超過1 cm.②不同數目的錨節點對定位精度產生的影響較大，拓撲4的PCRLB=0.205 m，將拓撲1和拓撲4進行比較，可以看出定位精度提高了3 cm.

4 總結和展望

本文提出了一種基于UWB和IMU的融合定位方法，來實現傳感網中目標節點的位置追蹤.通過計算克拉美羅下限CRLB來表征融合定位方法的空間定位性能，驗證其在解決多徑和幾何拓撲問題上的有效性.通過計算后驗克拉美羅下限PCRLB來表征融合定位方法的時間定位性能，驗證其在累積誤差糾正上的有效性，為基于UWB和IMU融合定位算法的設計和仿真提供理論支持.實驗結果表明，本文提出的融合定位方法具有更好的時空定位性能，更能接近實際應用的理論精度下限.

然而，雖然基于UWB和IMU的融合定位方法相比于單一UWB定位或單一IMU定位方法能夠獲得更好的性能，但其還是會帶來一定的問題：1)設備復雜性問題.相對于單一的定位方法，融合定位方法必定會對硬件設計(如設備體積等)提出更高的要求，如何在滿足實際要求的情況下，設計融合定位裝置是未來工作中需要考慮和解決的.2)算法復雜性問題.融合定位過程中需要進行多源數據的處理，因此需要合適的融合算法對這些數據進行融合，融合算法帶來的算法復雜性問題也是實際應用中需要考慮和解決的.3)資源分配和功耗問題.單獨采用IMU方法時不需要部署錨節點，在目標間通信上節省了很大的資源，但UWB和IMU融合定位方法中，必不可少地需要進行目標節點與錨節點之間的資源分配和任務調度，同時相應的功耗也需要考量，因此，如何設計融合定位中的任務調度和通信處理，盡可能地降低系統功耗是我們下一步的研究重點.