考慮安裝誤差的圓柱摩擦輪接觸分析

周磊， 陸天煒 ，李永健， 鄔霞

(西南交通大學 a. 機械工程學院; b. 牽引動力國家重點實驗室,四川 成都 610031)

0 引言

圓柱摩擦輪傳動是利用兩個相互壓緊的摩擦輪之間的摩擦力傳遞動力。圓柱摩擦輪傳動因具有結構簡單、制造方便、傳動精度高、使用維修方便等優點而廣泛運用于礦山機械、精密測量儀器等領域中，如水泥回轉窯、三坐標劃線機、大型天文望遠鏡等。在圓柱摩擦輪傳動的實際安裝中，不可避免地存在安裝誤差，這些安裝誤差對圓柱摩擦輪的接觸受力產生了影響。

劉波等[1]考慮了安裝偏心對摩擦輪傳動精度的影響進行了分析。肖友剛等[2]對回轉窯托輪和滾圈在斜壓接觸的情況下進行了有限元分析。李學軍等[3]運用有限元方法對回轉窯支承結構托輪平行與呈最大偏斜角時的接觸問題進行了研究。黃傳清等[4] 27-29對軸線交叉時兩圓柱體的接觸問題進行了研究。

圓柱摩擦輪傳動時，受較大的壓緊力作用，在不考慮制造誤差和輪軸的彈性變形時，由于安裝誤差的存在，導致摩擦輪的表面接觸區受力情況的改變，可能會使摩擦輪表面因應力集中而產生接觸疲勞破壞。本文利用ANSYSWorkbench對3種安裝誤差情況進行摩擦輪有限元接觸分析。分析結果對圓柱摩擦輪傳動的設計及安裝有一定的指導意義。

1 正確安裝圓柱摩擦輪的接觸分析

在不考慮制造誤差等其他因素時圓柱摩擦輪傳動正確安裝狀態如圖1(a)所示。圓柱摩擦輪的主動輪和從動輪在壓緊力Q的作用下產生接觸，可利用赫茲理論進行靜態接觸分析。主動輪和從動輪的接觸情況如圖1(b)所示，接觸區寬度為2a，長度為B的矩形，壓力分布為p(x)[5]:

(1)

其中，P=Q/B，a為半接觸寬度，由式(2)得到:

(2)

接觸區的最大接觸應力在接觸區中間并由式(3)得到：

(3)

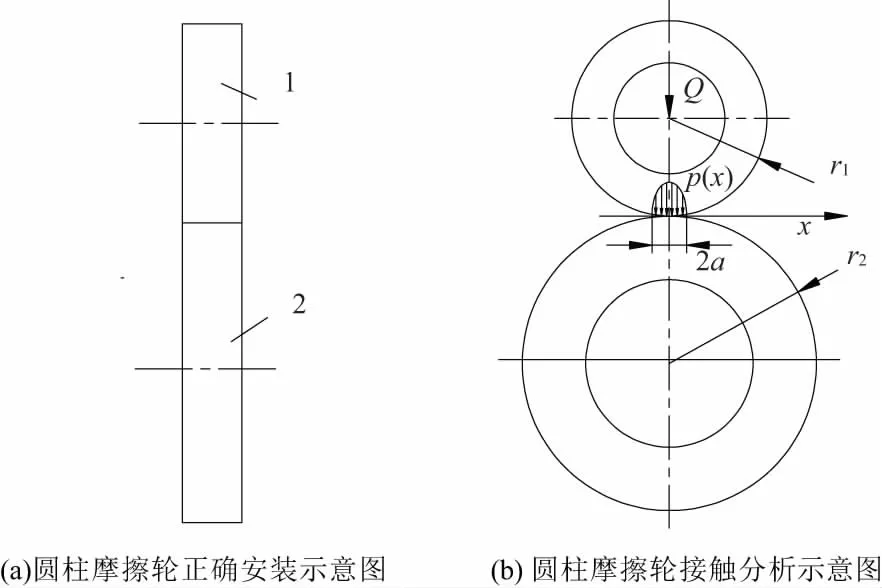
圖1 圓柱摩擦輪安裝

2 安裝誤差對圓柱摩擦輪接觸的影響

2.1 安裝偏心

安裝偏心指圓柱摩擦輪的回轉中心和幾何中心不重合，會導致圓柱摩擦輪在轉動的過程中心距不斷變化，當加壓裝置為恒壓加壓時，圓柱摩擦輪的壓緊力也不斷變化。如圖2所示，主動輪和從動輪的幾何中心和回轉中心分別為o1、o2和o3、o4；e1、e2分別為主動輪和從動的偏心距；r1、r2分別為主動輪和從動輪的半徑。現只考慮安裝偏心對圓柱摩擦輪接觸應力增加最嚴重的情況，為便于分析作如下假設：

1) 圓柱摩擦輪的壓緊力由彈簧產生，彈簧剛度為k；

2) 兩輪初始回轉中心距為l0=r1+r2-(e1+e2)，初始壓緊力為Q0；

3) 僅考慮壓緊力對兩輪靜態接觸的影響。

基于上面的假設，當主動輪與從動輪的回轉中心距達到最大值時，即lh=r1+r2+(e1+e2)，壓緊力也達到最大值Qm=Q0+2k(e1+e2)，將Qm帶入式(3)即可求得接觸區的最大接觸應力。

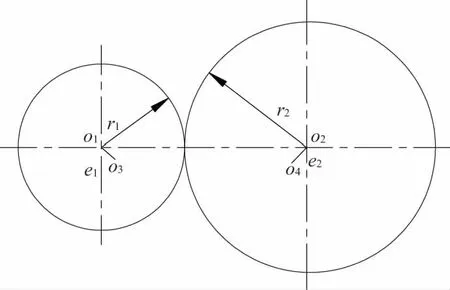
圖2 安裝偏心示意圖

2.2 扭轉角和偏轉角

由于安裝誤差，主動輪和從動輪的軸線在空間位置的角度可分解到兩個方向的夾角[6]，圖3中，α為偏轉角，β為扭轉角。

如圖3(a)所示，當主動輪和從動輪的軸線存在偏轉角時，主動輪和從動輪的接觸從線接觸變為點接觸，從而使初始接觸點處的接觸應力變大。

如圖3(b)所示，當主動輪和從動輪的軸線存在扭轉角時，初始接觸由線接觸變成點接觸，且該點位于線接觸時初始接觸線的中點。當扭轉角較小時，接觸區為不完全橢圓[4]27。

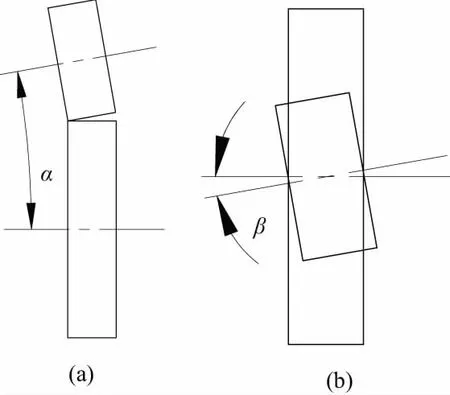
圖3 夾角示意圖

3 ANSYSWorkbench圓柱摩擦輪接觸分析

如圖4所示，為某實驗臺的圓柱摩擦輪傳動。現以該傳動為例，分別考慮正常安裝和存在安裝誤差的情況下，利用Workbench進行接觸分析，得到不同安裝條件下摩擦輪的接觸應力情況。此圓柱摩擦輪傳動采用恒壓壓緊裝置，壓緊力由普通圓柱螺旋彈簧產生；從動輪的滾動軸承座固定在直線導軌上，主動輪的軸承座固定在機架上；摩擦輪材料為鋼對鋼，無潤滑，摩擦系數取0.15[7]，詳細參數見表1。

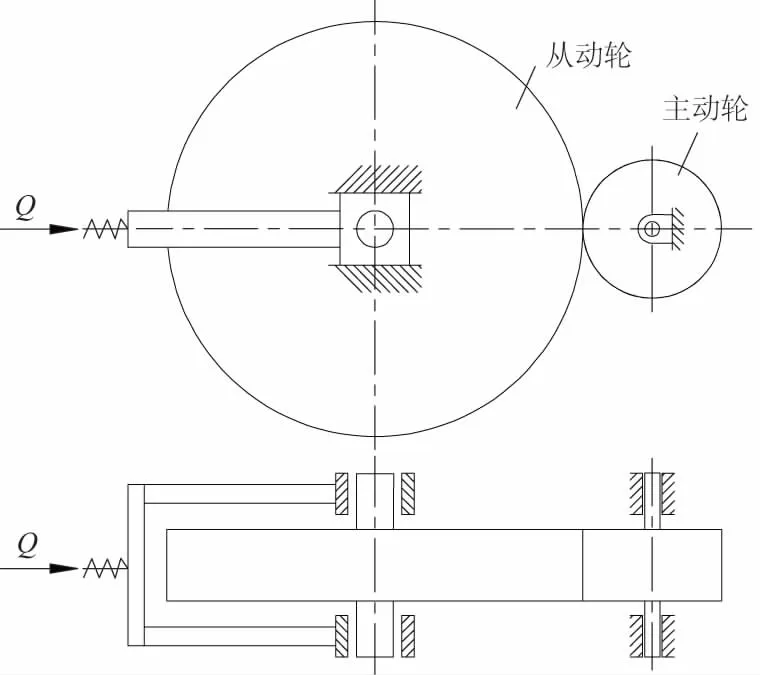
圖4 圓柱摩擦輪傳動示意圖

表1 圓柱摩擦輪的基本參數

3.1 有限元模型

忽略鍵槽倒角等細節部分，將兩輪簡化為兩個空心圓柱，按照表1中的參數建立圓柱摩擦輪的三維模型。為方便對摩擦輪進行網格劃分，將主動輪和從動輪分別分割成3個區域如圖5所示。對圓柱摩擦輪三維模型進行網格劃分，并對接觸區進行局部網格細化，細化單元大小為0.05 mm，如圖6所示，模型網格劃分后共48 613個單元，節點為170 606個。

網格劃分完后，定義接觸對：將主動輪接觸區表面定義為接觸面，從動輪接觸區表面定義為目標面；接觸類型設置為frictional，摩擦系數取0.15；接觸算法采用增強拉格朗日法。

根據圓柱摩擦輪的受力情況，主、從動輪施加載荷邊界條件如圖7所示，在主動輪的內孔面施加固定約束；在從動輪的內孔面施加給定位移約束，并設定兩輪接觸面的公法線方向自由度為無約束，其他兩個方向為0；在從動輪內孔面施加軸承載荷，模擬主、從動輪之間的壓緊力,并設置載荷步數為2。

圖5 分割模型

圖6 網格劃分

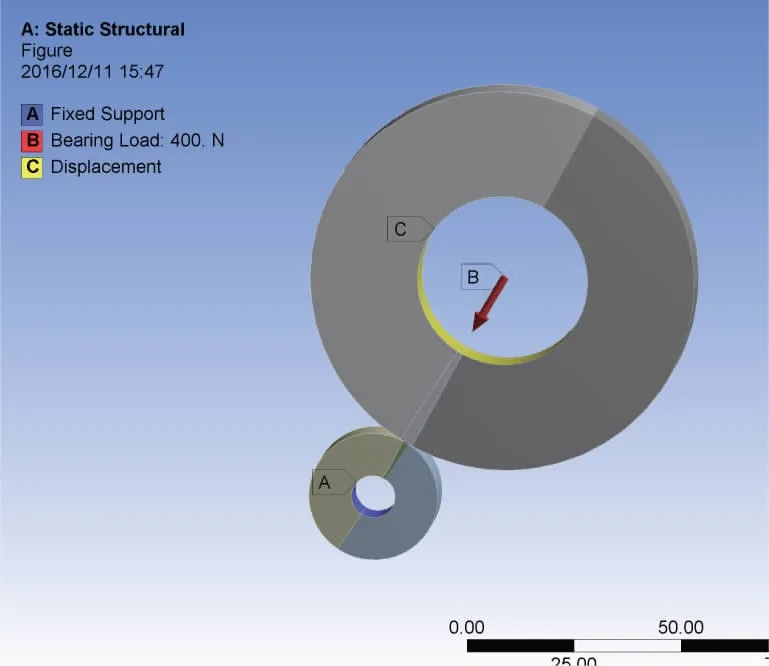
圖7 邊界條件和載荷

3.2 仿真結果及分析

經過仿真計算得到各安裝狀況下的圓柱摩擦輪的接觸應力。如圖8(a)所示，正確安裝時圓柱摩擦輪接觸區為狹長矩形，最大接觸應力為506.45 MPa和式(3)得到的理論值506.16 MPa基本一致；如圖8(b)所示，在摩擦輪的端面接觸區的最大接觸應力有所減小，這是由于端部材料受接觸壓力的作用時能夠在軸線方向變形所導致的，表明與赫茲理論相比有限元仿真更符合實際。

圖9(a)和圖9(b)分別為偏心距e1+e2=0.3mm和e1+e2=0.6mm時圓柱摩擦輪的接觸應力圖。由圖可知，當圓柱摩擦輪存在安裝偏心時，其接觸應力分布情況與正確安裝時基本一致，最大接觸應力有所增加,圖9(a)和圖9(b)中最大接觸應力比正常安裝時的最大接觸應力分別增加了1.53%、2.99%。

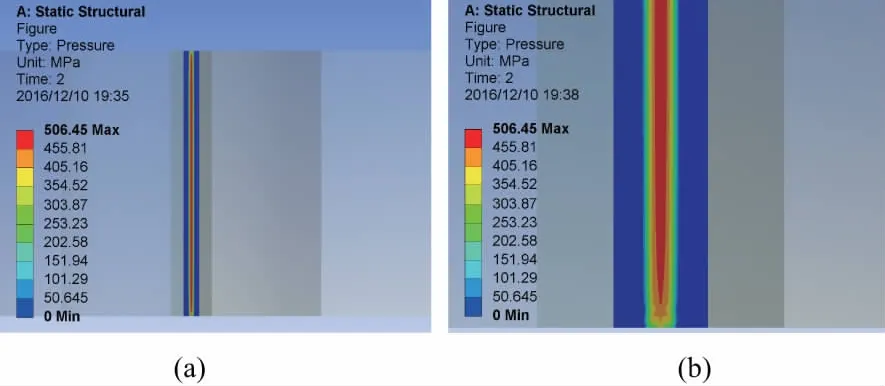
圖8 正確安裝時圓柱摩擦輪接觸應力圖

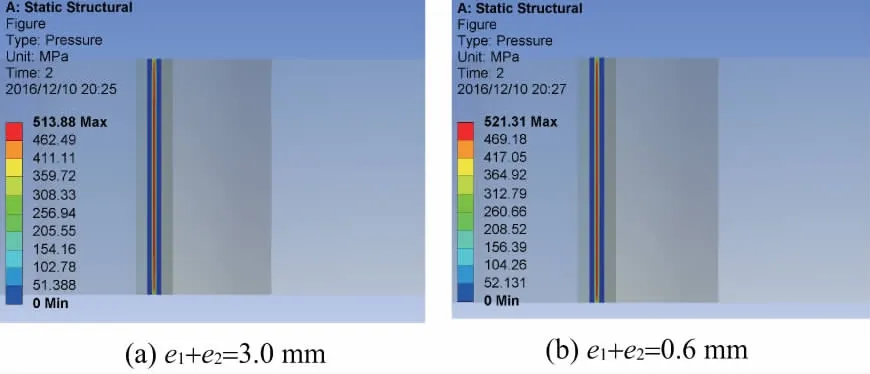
圖9 安裝偏心時圓柱摩擦輪接觸應力圖

圖10(a)和圖10(b)分別為偏轉角α=0.1°和α=0.4°時圓柱摩擦輪的接觸應力情況。可以看出，由于主動輪和從動輪的軸線存在偏轉角，接觸區由正常安裝時的狹長矩形變成近似半橢圓形狀，接觸壓力最大值靠近端部，且由最大值處沿半橢圓的長軸方向急劇減小。當偏轉角α=0.1°時，最大接觸應力為1 009.9 MPa，比正常安裝時增加了99.41%；當偏轉角α=0.4°時，最大接觸應力為1 581.7 MPa，比正常安裝時增加了212.32%。由圖10(a)和圖10(b)可以發現，隨著偏轉角增大，接觸區的大小也隨之變小。

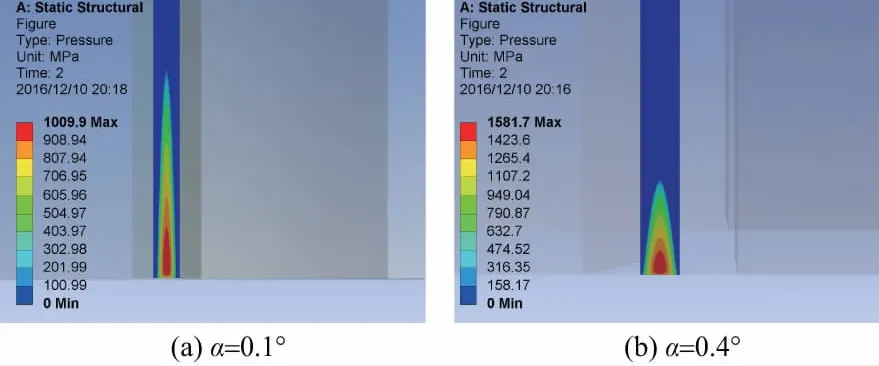
圖10 安裝存在偏轉角時圓柱摩擦輪接觸應力圖

當圓柱摩擦輪安裝存在扭轉角時的接觸應力情況如圖11所示。由圖11可知，接觸應力分布與正確安裝時差別不大，但最大接觸應力增加。當扭轉角β=0.1°時，最大接觸應力為509.85MPa，當扭轉角β=0.4°時，最大接觸應力522.19MPa，與正常安裝時分別增加了0.73%與2.62%。

仿真還得到了在各類安裝誤差情況下摩擦輪最大接觸應力隨安裝誤差的大小的變化情況。如圖12(a)、圖12(b)和圖12(c)所示，最大接觸應力隨安裝誤差增大而增大。圖12(a)為彈簧剛度分別為31 N/mm、41 N/mm、51 N/mm時，摩擦輪的最大接觸應力與偏心距的關系。由圖12(a)可知，摩擦輪的最大接觸應力隨偏心距的增大而增大，同時偏心距對最大接觸應力的影響程度還隨彈簧剛度的增加而增加。比較圖12(b)和圖12(c)，偏轉角比扭轉角更容易造成摩擦輪的偏載和應力集中，導致最大接觸應力急劇變大。

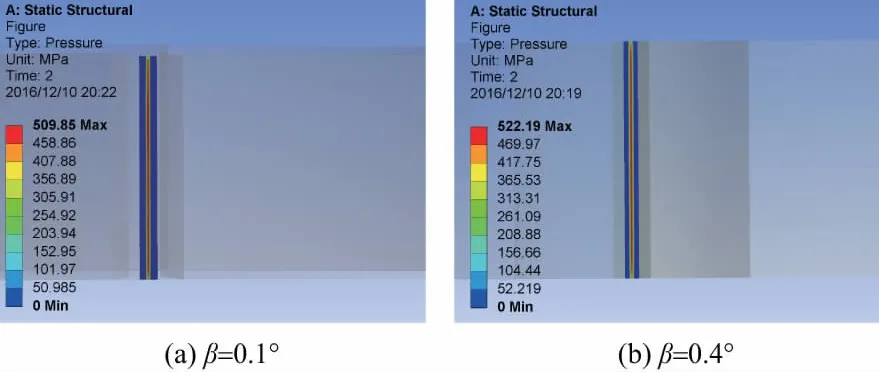
圖11 安裝存在扭轉角時圓柱摩擦輪接觸應力圖

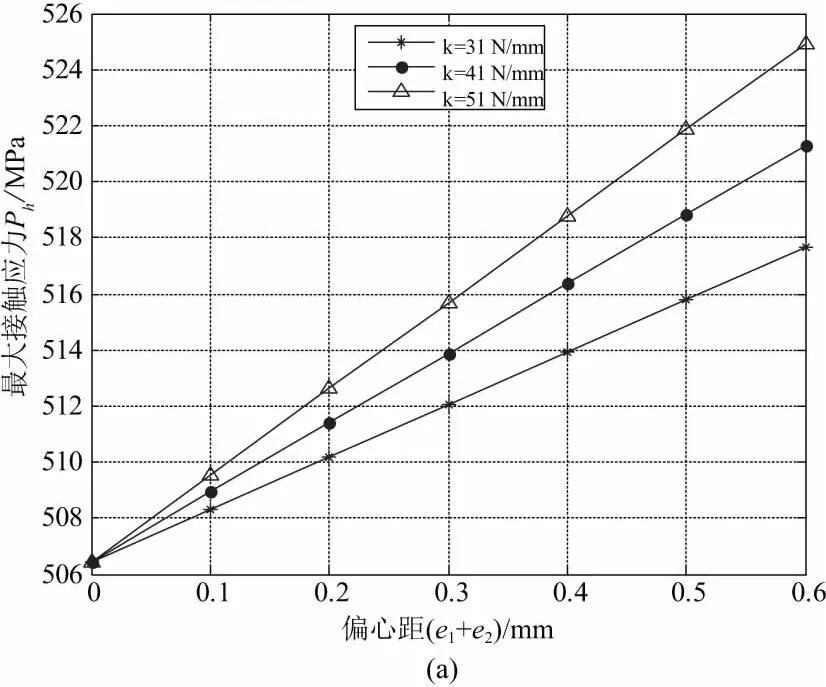
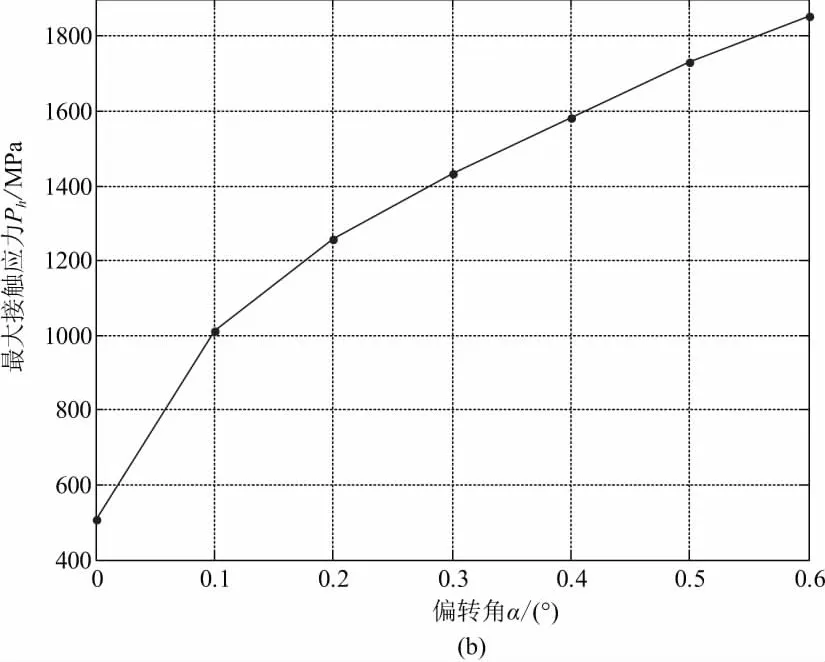
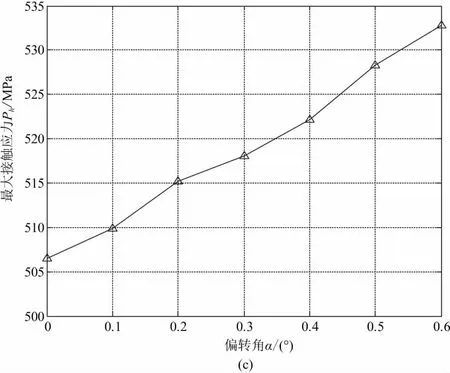
圖12 圓柱摩擦輪最大接觸應力圖

4 結語

通過對圓柱摩擦輪傳動在正確安裝和存在安裝誤差時摩擦輪接觸情況的分析，并利用ANSYSWorkbench對一對圓柱摩擦輪傳動在不同安裝條件下進行了接觸仿真分析，可得到如下結論：

1) 赫茲理論對圓柱摩擦輪的接觸分析在接觸區的大部分區域適用，但在圓柱摩擦輪的端部有所偏差，有限元分析更符合實際。

2) 安裝時存在偏轉角會導致摩擦輪接觸產生嚴重的偏載和應力集中，最大接觸應力也隨之增大而急劇增加，其對圓柱摩擦輪接觸的影響比存在扭轉角時更大。

3) 安裝偏心對圓柱摩擦輪接觸的影響還與彈簧剛度有關；存在相同的安裝偏心時，所用彈簧剛度越大，摩擦輪的最大接觸應力也增加得越多。

4) 在實際圓柱摩擦輪的設計和安裝中，應該合理設計彈簧的剛度以減小安裝偏心對摩擦輪最大接觸應力的影響；安裝時應盡量避免存在偏轉角和扭轉角以防止應力集中和偏載。