基于主成分分析的高速銑削振動特性研究

林蓋，林述溫

(福州大學 機械工程及自動化學院,福建 福州 350108)

0 引言

隨著現代社會對材料質量的需求越來越高，大量高精高效技術正快速發展。鈦合金作為一種重要的結構金屬，當采用高速加工時，還是高度依賴機床操作人員的技術和經驗，難以預測加工表面質量。這是因為加工面的形成不僅與刀具的幾何形狀和切削參數有關，還與刀具和工件的振動特性有關[1-2]。刀具和工件的振動作為一種可通過相關設備實時監測的現象，有助于強化對表面質量的預測，所以高速銑削的振動特性引起了許多研究者的極大興趣[3]。

高速銑削的振動特性已經進行了許多研究，但都著重于對振動特性的描述，很少研究振動特性對表面質量的影響[4-7]。這主要是因為振動信號形式多樣，數據結構復雜，難以找出穩定且簡單的振動特征量。因此，本文用統計學的一些方法，研究振動信號的特征。

功率譜密度(power spectral density，PSD)是具有綜合分析意義的概率統計函數，從頻域上考慮問題，研究隨機振動各頻率成分的功率分布情況。隨機過程X(t)的功率譜密度為:

(1)

其中FX(ω,T)是XT(t)的傅里葉變換。

主成分分析(principal component analysis，PCA)就是利用降維的思想，將原有的多個指標轉化為少數幾個有代表性的綜合指標，這些指標能反映原來指標的大部分信息(85%以上)，并且各個指標之間保持相互獨立。

1 實驗設備與實驗方案

1.1 實驗設備

實驗采用5軸立式銑削加工中心MAZAK VARIAXIS 500-5XⅡ，其主電機功率為22.4 kW，最高轉速達12 000 r/min。刀具選用直徑為10 mm的涂層硬質合金立銑刀，材料為鎢鋼，齒數為4。實驗工件材料為鈦合金Ti6Al4V(TC4)，尺寸規格為100 mm×80 mm×20 mm。振動信號采集系統包括：振動信號采集儀器 LMS Test.Xpress及其配套軟件、壓電式傳感器和計算機，以及Marsurf XCR20馬爾粗糙度儀測量表面粗糙度。

1.2 實驗方案

受實驗條件所限，為保證實驗數據充足，分別考慮5mm和10mm兩組銑削寬度，選擇L9(34)的正交表，設計兩組正交實驗，因素水平見表1。

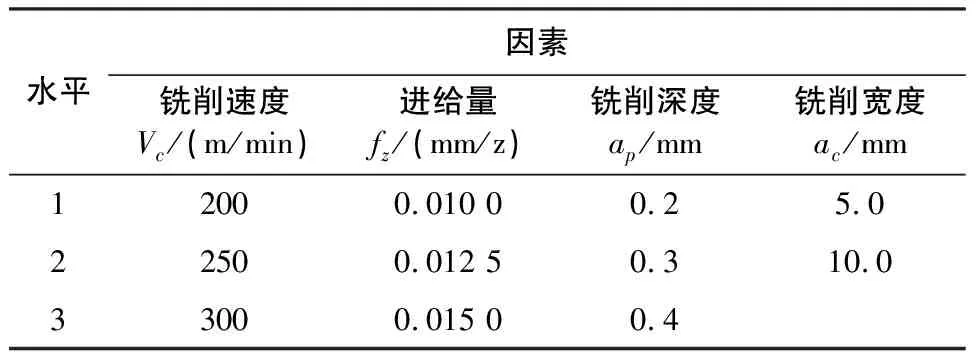
表1 實驗因素水平表

實驗過程中采用順銑的方式加工工件。由于刀具和工件之間的相對振動難以直接測量，且主要考慮銑削過程中銑削力周期變化引起的自激振動和刀具斷續切削等復雜切削機理引起的強迫振動[3]，因此選擇將測點布置在刀具和工件的臨近部位。在主軸和工作臺的x、y、z3個方向上布置加速度傳感器，測量該部位的加速度振動信號。x表示銑削進給運動方向，y表示銑削寬度方向，z表示銑削深度方向。具體實驗環境如圖1。

圖1 傳感器布置及銑削中心坐標軸示意圖

2 實驗數據處理與分析

2.1 實驗數據處理

在實驗過程中，用LMS振動信號采集系統測量每組實驗3次走刀的加速度振動信號，并對振動信號做功率譜分析，部分實驗結果見圖2、圖3。用馬爾粗糙度儀測量每次走刀形成表面的表面粗糙度值，每刀測量3次，最后取9次的平均值。表面粗糙度測量結果見表2。

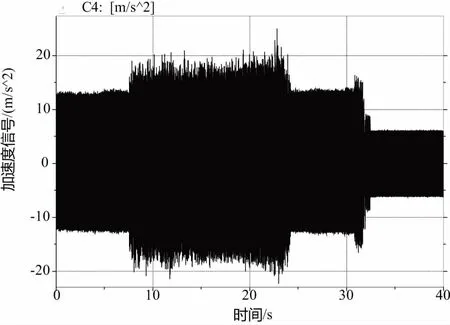
圖2 加速度振動信號

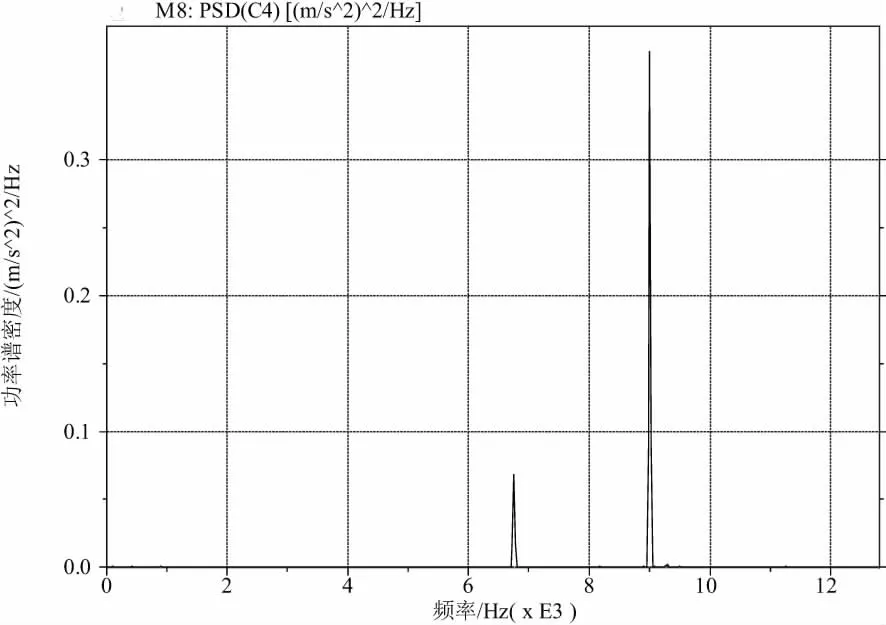
圖3 加速度振動信號的功率譜密度

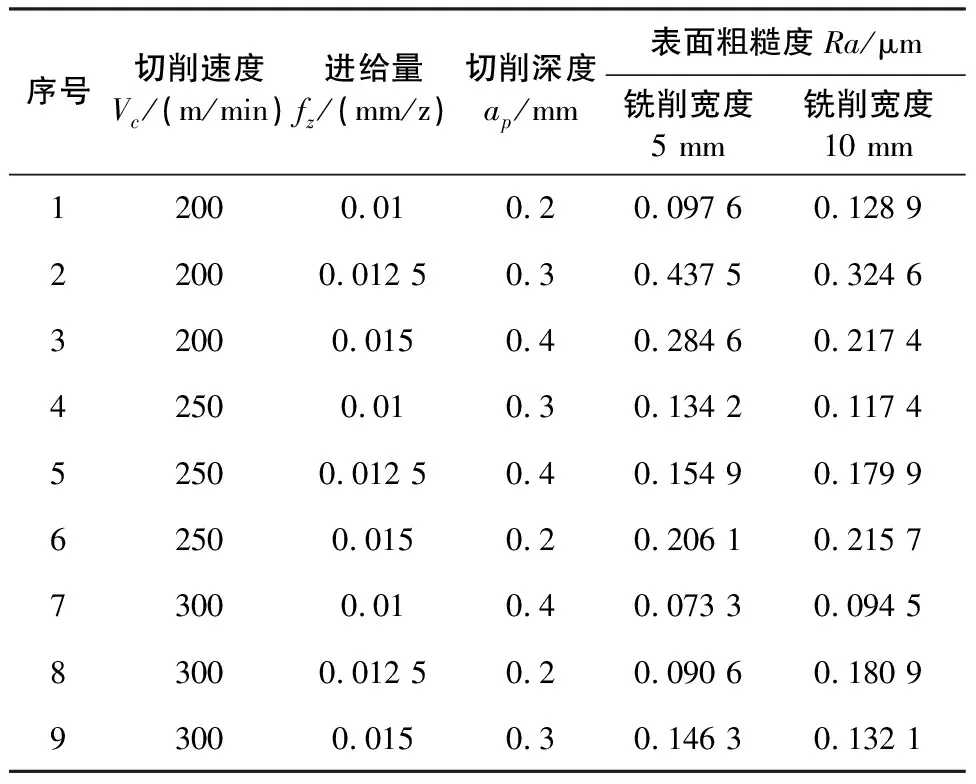
表2 正交實驗方案下的表面粗糙度值

2.2 實驗數據分析

在分別對主軸和工作臺x、y、z3個方向上的振動信號做功率譜分析后發現，振動信號頻率分布基本一致，主要集中在2個高頻成分6 760Hz和9 000Hz，只有極少數存在微小偏差，低頻成分所占比例極小，可以忽略不計。所以從6 760Hz和9 000Hz 2個頻率成分的功率譜幅值研究高頻振動對表面粗糙度的影響。

首先分析頻率為6 760Hz的功率譜幅值對表面粗糙度的影響規律，18組實驗數據如表3所示。

表3 主軸和工作臺3個方向上的振動信號頻率6 760 HZ處的功率譜幅值

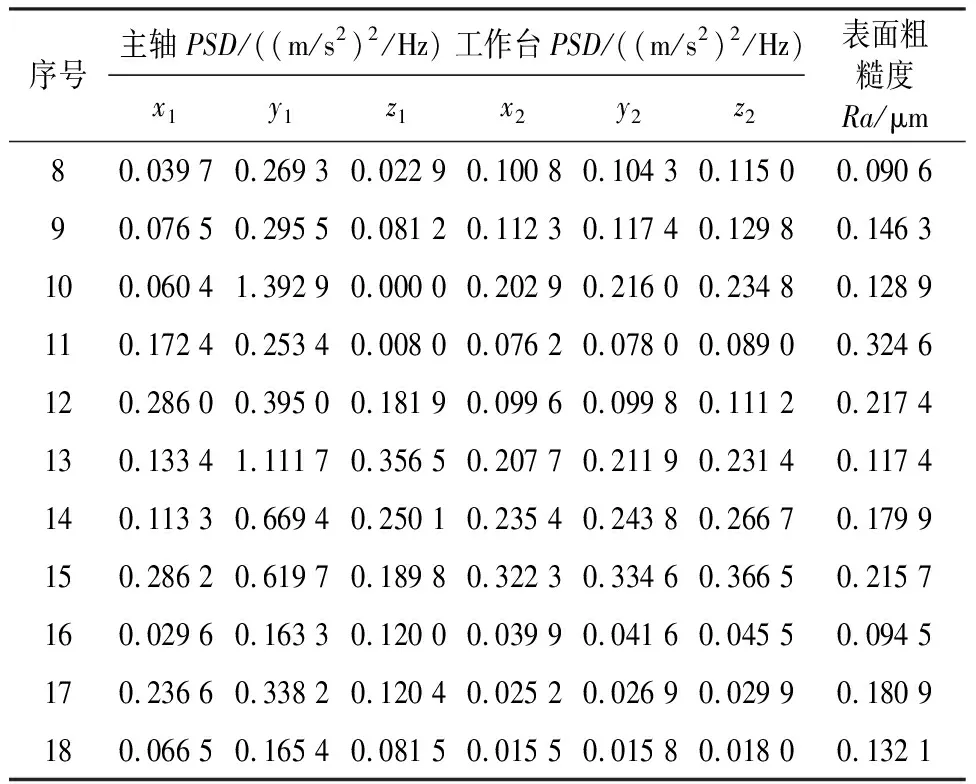
續表3

從表3不難看出，振動信號數據結構依然復雜，難以看出這些功率譜密度數據與表面粗糙度的關系。假設這些數據與表面粗糙度值存在線性關系，利用SPSS軟件進行多元線性回歸分析，對數據的自相關性和共線性進行診斷，分析結果如表4所示。

表4 系數及共線性診斷表

通過線性檢驗得到調整R2為0.598，說明該線性回歸模型與原數據的擬合程度不高；6個變量經過t檢驗，只有x1的置信度<0.05，即說明主軸x方向上的振動信號功率譜幅值對表面粗糙度值的影響是顯著的；共線性診斷統計量中，若VIF統計量>10，則說明數據之間的共線性層度小，可忽略不計，x2、y2、z2的VIF值遠大于10，說明數據之間共線性層度較高，需對數據結構進行簡化處理。

先對數據進行探索性研究，利用因子分析法中主成分分析法對數據進行降維處理(見表5)。

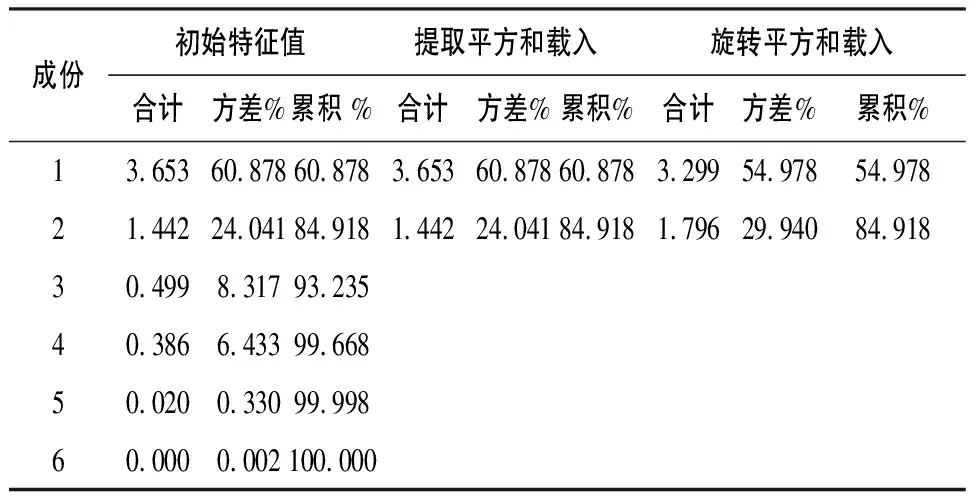
表5 成分信息含量

對數據進行主成分分析適度檢驗發現KMO值較低，表示數據量不夠，但通過了Bartlett球形檢驗。從整體上看，雖然實驗數據不足，但依然可以進行主成分分析。

從表5可以看出，主成分前2項就可以涵蓋原始數據近85%的信息量，所以可以用這2項指標代表前面的6項指標。從后面的成分旋轉矩陣可以看出成分1主要表示工作臺3個方向的功率譜幅值，成分2主要表示主軸x和z方向上的功率譜幅值，而主軸y方向的功率譜幅值沒有體現在表中，這可能是因為該數據成分比較均衡地分布在兩個主成分中。

雖然存在誤差，但不難看出主成分分析方法能夠有效區分主軸和工作臺的振動信號。可以合理猜測，隨著數據量的提升，主成分分析法對數據的分類就越精確，這說明該方法有助于高速銑削振動信號的特征分類。

對9 000Hz處的功率譜幅值數據做相同處理。

先假定6個變量與表面粗糙度存在線性關系，進行自相關和共線性檢測，經SPSS數據處理后發現，調整R2為0.41，說明該線性擬合模型僅能反映原始數據的41%；t檢驗的顯著性水平只有x1低于0.05，說明主軸x方向上9 000Hz處的功率譜幅值對表面粗糙度的影響是顯著的；通過共線性診斷發現，x2、y2、z2處的VIF值遠大于10，故判斷數據間存在多重共線性，需對數據簡化處理。

通過SPSS軟件對9 000Hz處的功率譜幅值數據做主成分分析，結果顯示，前2項主成分反映原始數據的84.824%，將近85%，可以用2個主成分表示原始數據。第1個主成分主要反映工作臺3個方向上的功率譜幅值，第2個主成分主要反映主軸3個方向上的功率譜幅值。

整體上看，主軸x方向上的振動信號對表面粗糙度的影響程度最大，同一部位不同方向上的功率譜幅值存在多重共線性，利用這一點可以大大簡化數據結構，但這些數據特點還不能反映各部位兩高階頻率的功率譜幅值對表面粗糙度的影響程度。從多元線性回歸分析結果可以看出，這些變量與表面粗糙度的線性擬合程度很低，不適合直接做線性回歸。根據一些專家學者的研究[8]，表面粗糙度與銑削參數之間的關系可用指數模型表示，所以假定表面粗糙度與振動特性參數的關系是指數關系，那么可以先求出數據的對數值，再利用SPSS軟件進行多元線性回歸分析，即可求出回歸模型。

3 求解回歸模型

3.1 振動信號的功率譜幅值的處理方案

通過之前的數據分析可以發現6 760Hz和9 000Hz的功率譜幅值都分別存在多重共線性，但并不能判斷兩組數據之間不存在線性關系，故綜合所有振動信號數據進行主成分分析，結果如表6。

適度檢驗結果中KMO值為0.506，數據量略有不足，但通過了Bartlett球形檢驗，表明這些數據使用主成分分析是較為合理的。從表6可以看到前3項主成分能涵蓋原始數據89.719%的信息，可將這些信息分為3類，每一類主成分中的變量之間存在線性關系。第1類主成分涵蓋了工作臺90%以上的振動信息，第2類主成分主要包括主軸y和z方向的振動信息，第3類主成分則包含了主軸x方向上的振動信息。

表6 成分信息含量

由于同一主成分內的變量間存在線性關系，故可用1個變量表示該成分的振動特性，選擇主成分內原始信息含量最高的變量作為影響表面粗糙度的因素，因此選擇工作臺y方向9 000Hz處的功率譜幅值、主軸y方向9 000Hz功率譜幅值和主軸x方向6 760Hz處的功率譜幅值3個變量作為振動特征量。各個振動特征量與其組內其他變量的線性關系通過線性回歸得到，結果如式(2)-式(4)所示。

第1主成分：

y高2=1.027x高2-0.067=

0.966z高2-0.095=

5.133x低2+0.512=

5.004y低2+0.524=

4.473z低2+0.513

(2)

第2主成分：

y高1=5.094y低1+0.894=

1.209z高1+2.894=

7.185z低1+2.860

(3)

第3主成分：

x低1=0.148x高1+0.017

(4)

式中，角標“低”指6 760Hz，角標“高”指9 000Hz，角標“1”表示主軸，角標“2”表示工作臺。

綜合前述分析和式(2)-式(4)可知，9 000Hz處的功率譜密度幅值對表面粗糙度的影響程度比6 760Hz處的大，即高頻振動對表面粗糙度的影響較大；x方向上的功率譜密度幅值對表面粗糙度的影響程度比其它方向大，即刀具進給方向的振動特性對表面粗糙度的影響較大。

3.2 建立指數模型

由于試驗中銑削寬度只選擇了2個水平，且銑削寬度對表面粗糙度的影響并不顯著，所以這里計算時忽略銑削寬度，這給數據分析帶來一定的誤差。

假定表面粗糙度與銑削工藝參數和振動特征量之間存在指數關系，先計算銑削工藝參數、振動特征量和表面粗糙度的對數值，再利用SPSS軟件進行多元線性回歸分析(表7)。

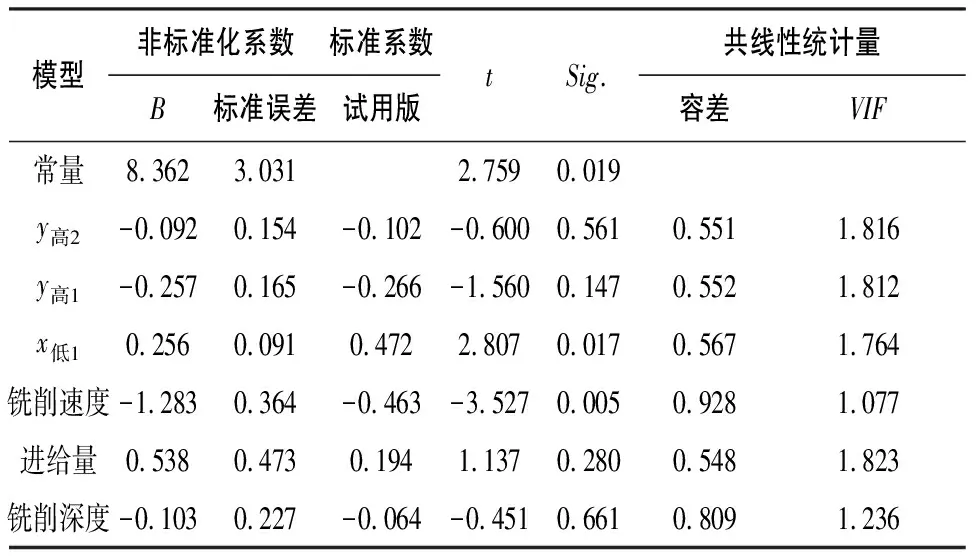
表7 系數檢驗表

該分析得到調整R2值為0.727，說明該回歸模型能反映原始數據72.7%的信息量，DW統計量接近2，說明每組數據之間的自相關程度非常低，即每組實驗數據之間相互獨立。所以該模型能比較完善地反映表面粗糙度、銑削參數和振動特征量的關系。

從表7可以看出各因素對表面粗糙度的影響程度。通過t檢驗的結果可以知道，銑削速度對表面粗糙度的影響最為顯著，其次影響程度從高到低是主軸x方向6 760Hz(主成分3)、主軸y方向9 000Hz(主成分2)、進給量、工作臺y方向9 000Hz(主成分1)和銑削深度。進給量、銑削深度、主成分1對表面粗糙度的影響程度都非常低，分析原因有兩點：從實驗設計上看，設計的是三因素三水平的正交試驗，進給量和銑削深度因為實驗條件限制的原因設定范圍非常小，因而對表面粗糙度的影響較小；從振動形式上看，工作臺處于固定狀態，主軸在加工時一直保持高速旋轉，主軸的振動屬于自激振動，工作臺的振動屬于強迫振動，高速銑削過程中自激振動往往強于強迫振動，自激振動在刀具和工件之間相對振動中起主導作用，所以工作臺的振動特性對表面粗糙度的影響程度非常小。

綜上所述，高速銑削鈦合金表面粗糙度與銑削參數、各振動特征量之間的指數關系式為：

(5)

式中，z1表示第1個主成分中工作臺y方向9 000Hz處的功率譜幅值，z2表示第2個主成分中主軸y方向9 000Hz功率譜幅值，z3表示第3個主成分中主軸x方向6760Hz處的功率譜幅值。

結合前面的分析和式(5)可以看出高頻處功率譜幅值對表面粗糙度的影響是比較顯著的，特別是x方向，即刀具進給運動方向的振動特性。這一點說明在高速銑削過程中主軸和工作臺的高頻振動特性對加工表面粗糙度的影響較大。由于主軸和工作臺的高頻動態特性不僅與自身固有屬性有關，還與外界激勵，如環境噪聲、銑削用量等有關。因此，一方面可以通過提升主軸和工作臺的強度和剛度來改善該部位的高頻動態特性；另一方面可以通過合理設置銑削參數，使主軸和工作臺的高頻動態特性控制在適當的狀態，進一步改善加工質量。具體的改善措施還有待深入研究。

4 結語

基于振動信號功率譜分析，研究了高速銑削鈦合金振動特性對表面粗糙度的影響規律，通過主成分分析法簡化了振動信號數據量，并用多元線性回歸分析得到表面粗糙度關于振動特征量和銑削參數的指數回歸模型。具體得到以下結論：

通過共線性檢測發現振動信號功率譜幅值之間存在多重共線性，將振動信號數據進行主成分分析，發現這些數據可分為3類，第1類為工作臺的振動信號，第2類為主軸y、z方向的振動信號，第3類為主軸x方向的振動信號。

結合主成分分析和線性回歸分析可知，9 000Hz處的功率譜密度幅值對表面粗糙度的影響程度比6 760Hz處的高，即高頻振動對表面粗糙度的影響較大；x方向上的功率譜密度幅值對表面粗糙度的影響程度比其他方向高，即刀具進給方向的振動特性對表面粗糙度的影響較大。

通過多元線性回歸得到表面粗糙度關于振動特征量和銑削參數的指數回歸模型，并指出可以通過改善主軸和工作臺的強度、剛度和設置合理的銑削參數來提升加工表面質量。