三缸發動機平衡系統彈性齒輪力學特性分析
姜曉帥,李剛炎,王平俊,熊峰
(武漢理工大學 機電工程學院, 湖北 武漢 430070)
0 引言
彈性齒輪是指腹板具有一定柔性的齒輪,又稱為柔性腹板齒輪[1-2]。彈性齒輪能夠減小輪齒接觸應力[1] 43,降低傳動過程中的振動和噪聲[2-5],廣泛地應用在機械傳動系統中,也因此成為國內外眾多學者研究的重點,在結構方面,顧玉華[2] 15-16、Helmut Swars[3]等提出了在齒輪腹板上添加柔性件的彈性齒輪設計,輪轂和齒圈為一個整體;王建軍[5]提出了齒圈與輪轂分離式的彈性齒輪,通過螺栓或鍵連接的方式在齒圈與輪轂中間附加橡膠;黎冠中、戚文星[6]介紹了多種形式的彈性齒輪制作和橡膠材料的研究。雖然國內外對齒輪的研究已有很多,但對彈性齒輪橡膠參數對其應力應變的影響的相關研究鮮見,而齒輪接觸疲勞強度和齒根疲勞強度是避免齒輪發生齒面磨損或齒根斷裂等破壞現象,并保障設備運行安全、可靠的關鍵,因此,本文的研究具有一定的工程指導意義。
1 彈性齒輪及其參數化模型
1.1 彈性齒輪結構與功用
三缸發動機平衡系統彈性齒輪由輪轂、橡膠和外齒圈3部分組成。輪轂和外齒圈采用分離式設計,由粉末冶金工藝制造而成,不通過螺栓或鍵等機械方式聯接,而是通過橡膠硫化工藝在二者中間形成一定厚度的橡膠環,同時,將輪轂和外齒圈粘接成為一個整體,彈性齒輪結構如圖1所示。彈性齒輪粉末冶金材料為FC-0205-80HT(美國MPIF標準35),橡膠材料為氫化丁腈膠(HNBR,hydrogenate nitrile)。

圖1 彈性齒輪結構
發動機平衡系統彈性齒輪作為發動機曲軸與平衡軸之間的傳動構件,保證平衡軸與曲軸之間按一定轉速比旋轉,實現平衡發動機傾覆力矩的作用。同時,相對全金屬齒輪,彈性齒輪能夠降低傳動過程中的振動和噪聲。
1.2 彈性齒輪參數化模型
1) 齒輪參數
彈性齒輪為漸開線齒輪,模數為1.5,齒數67,壓力角20°,齒寬12mm,變位系數-1.332。
2) 齒廓方程
如圖2所示,以齒輪幾何中心o點為坐標原點,以齒厚對稱線為坐標系y軸,建立直角坐標系o-xy。實際的齒輪齒廓由齒頂圓圓弧AB,漸開線BC,齒根過渡圓CD和齒根圓圓弧DE組成。
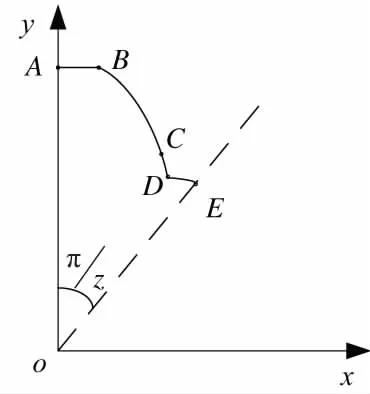
圖2 齒輪齒廓示意圖
在齒輪建模中,齒頂圓、齒根圓以及漸開線方程的建立已研究較多,這里不再贅述。齒根過渡圓曲線CD與齒輪的加工刀具參數有關,文獻[7] 給出了由齒條型刀具加工的齒輪齒根過渡圓曲線方程:
(1)
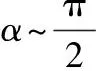
3) 參數化模型
基于以上彈性齒輪的參數與齒廓曲線,利用Pro/E軟件建立精確的齒輪模型如圖1(b)所示。
2 彈性齒輪有限元分析
2.1 彈性齒輪有限元分析理論
經典力學理論確定了物體動力學的通用方程為:
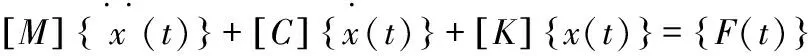
(2)

[K]{x}={F}
(3)
齒輪的受力和變形主要在嚙合傳動過程中,彈性齒輪橡膠結構必將對其綜合嚙合剛度帶來影響,繼而影響其力學特性。采用集中質量方法,將彈性齒輪外齒圈簡化為質量塊M;驅動齒輪與彈性齒輪外齒圈的嚙合剛度km和嚙合阻尼簡化cm為由彈簧和阻尼器構成的連接件;橡膠的扭轉剛度轉變為沿嚙合線方向的位移剛度kT與位移阻尼cT,同樣將其視為一個由彈簧和阻尼器構成的連接件。簡化后的兩個連接件為串聯關系,如圖 3 所示,ke、cm分別等效后的嚙合剛度和嚙合剛阻尼。
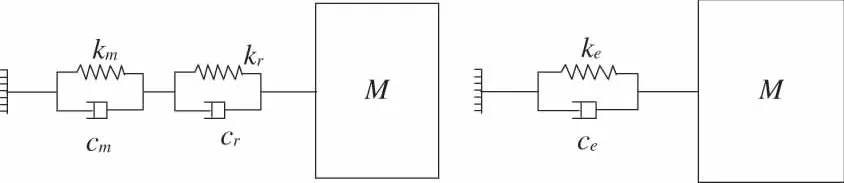
圖3 彈性齒輪嚙合剛度等效模型
由剛度的串聯關系可得,彈性齒輪等效嚙合剛度為:
(4)
2.2 材料及其參數
1) 粉末冶金材料參數
粉末冶金材料牌號為FC-0205-80HT,其楊氏模量為130 GPa,泊松比為0.27,密度為6.8 g/cm3。
2) 橡膠材料常數
根據橡膠本構關系模型選擇要求,結合彈性齒輪橡膠小變形等特點,選擇Mooney-Rivlin模型[9]作為橡膠的分析模型。HNBR為軟質橡膠,其硬度HS與Mooney-Rivlin模型中材料常數C10,C01之間的關系[10]為:
(5)
根據式(5),可確定不同橡膠硬度HS(HS55、HS60、HS65、HS70、HS75),不同C01/C10值[11](0.05、0.1、0.15、0.2、0.25)下的橡膠材料常數C10、C01的值。
2.3 彈性齒輪工況分析與邊界條件設置
彈性齒輪作為發動機的平衡系統的傳動構件,其轉速高、受變載荷沖擊頻繁,承受最大動態扭矩為40N·m,軸承、缸體等支撐剛度較大,忽略其彈性變形對齒輪受力的影響。
驅動齒輪與彈性齒輪的齒形及大小相同,設置對稱接觸,摩擦系數為0.08,考慮大變形影響,接觸剛度設為1.0;對兩齒輪均設置相對地面的轉動副,限制其他自由度,驅動齒輪設置轉速,彈性齒輪設置轉矩,因轉矩是影響齒輪受力情況的主要因素,考慮最惡劣工況下的齒輪受力情況,設置最大承載力矩為40N·m。
3 彈性齒輪應力與應變特性分析
3.1 彈性齒輪與全金屬齒輪應力與應變特性對比
取彈性齒輪橡膠參數:厚度為3.5mm,寬度為13mm,硬度HS60,C01/C10=0.25(經驗證C01/C10值對齒輪應力應變幾乎沒有影響)下材料常數。相同工況下,彈性齒輪和全金屬剛性齒輪的應力與應變如圖4—圖7所示。
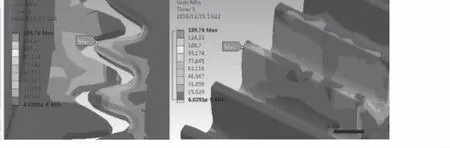
圖4 彈性齒輪應力

圖5 金屬齒輪應力
利用Hertz接觸理論求得全金屬齒輪的最大接觸應力約為193 MPa,誤差為5%,說明有限元分析結果正確。
由圖4、圖5可知,彈性齒輪和金屬齒輪的齒根部位應力較為集中,最大應力均出現在齒頂部位,符合齒輪受力特征。金屬齒輪最大應力為184 MPa,彈性齒輪最大應力為140 MPa,應力減少約24%,初步說明彈性齒輪降低了接觸應力,結論與文獻[1] 結果相符。

圖6 彈性齒輪應變

圖7 金屬齒輪應變
由圖6、圖7可知,全金屬齒輪應變集中與輪齒部位,彈性齒輪降低了輪齒接觸的應力變形,最大應變位置和主要應變位置由輪齒部位轉變為腹板處的橡膠部位,最大應變為0.309mm。這是因為橡膠比金屬材料強度、硬度小,而阻尼高,能夠吸收沖擊能量。
3.2 橡膠參數對彈性齒輪應力與應變的影響
在彈性齒輪有限元模型的基礎上,研究橡膠的硬度、厚度(沿齒輪徑向尺寸)和寬度(沿齒輪軸線尺寸)對彈性齒輪應力與應變的影響。
1) 正交實驗方案的設計
正交實驗設計[12]的關鍵在于明確實驗指標,確定實驗因素及水平,選擇合適的正交實驗表。本文以彈性齒輪應力與應變為分析指標,其值越小越好,選取橡膠的硬度、厚度和寬度作為正交實驗的考查因素。
在正交實驗中,一般實驗因素的水平以2~4個水平為宜,本文取3個因素水平。依據工程實際的要求和專業知識確定實驗的因素水平,選擇正交表L9(34),設計實驗方案并得到實驗結果如表1所示,表中數字(1,2,3)表示水平,括號內為對應的因素水平值。
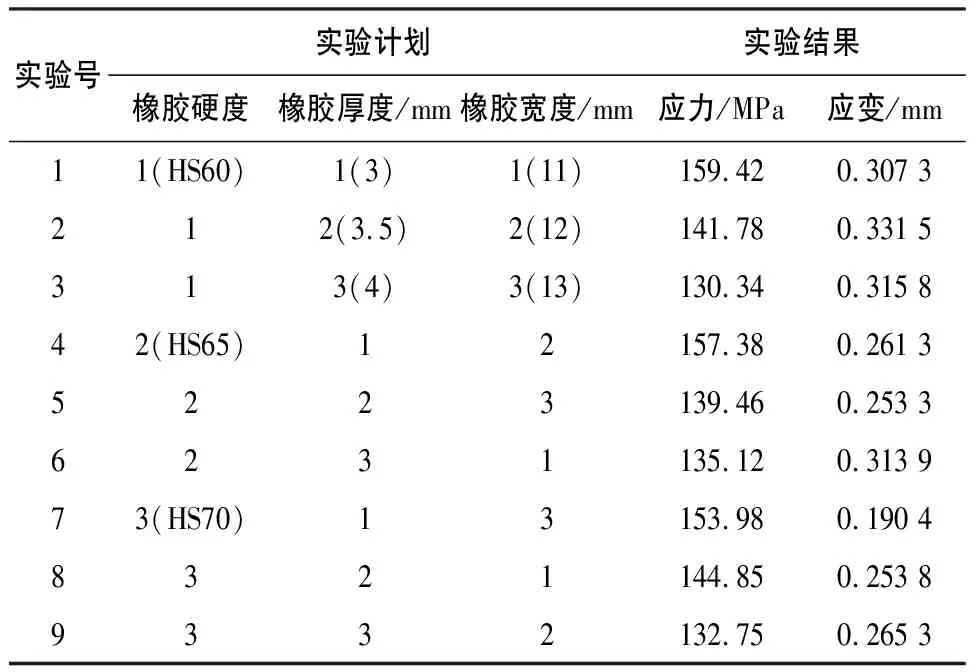
表1 實驗方案設計與結果
2) 結果的極差分析
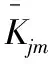
Rj為第j列因素的極差,其表達式為:
(6)
計算得到彈性齒輪應力與應變的極差如表2所示。
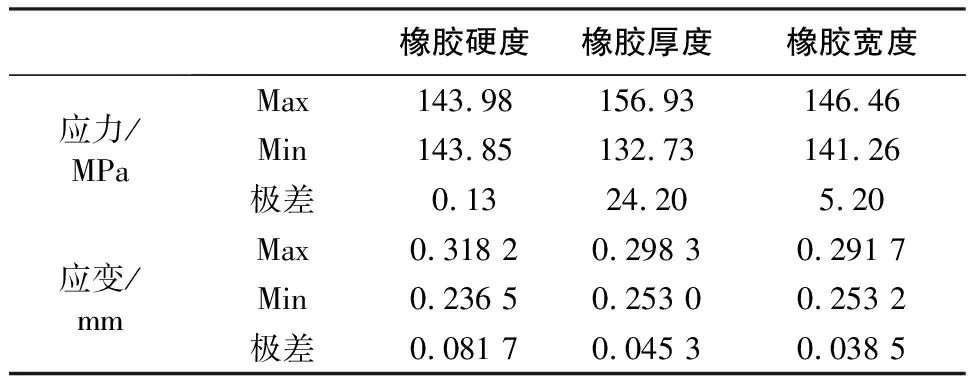
表2 彈性齒輪應力與應變極差分析
由表2可知,橡膠硬度對彈性齒輪應力影響極小,但對應變影響較大;橡膠厚度和寬度對彈性齒輪應力與應變均有影響,但影響程度有所不同。根據極差的大小可知,橡膠厚度對彈性齒輪的應力影響最大,橡膠寬度次之;橡膠硬度對彈性齒輪應變的影響最大,橡膠厚度次之,橡膠寬度最小。
3) 結果的方差分析
由于極差不能給出判斷因素對結果影響是否顯著的標準,因此對其進行方差分析,將結果進行偏差平方和分解,構造F統計量,生成方差統計表,利用P值法判斷各因素對結果影響的顯著性。P值是顯著性概率,P值越小,表示該因素對結果的影響程度越大,當P值<0.05時認為該因素對結果有顯著影響,各因素P值如表3所示。

表3 因素顯著性分析
由表3可知,在應力方面,橡膠厚度的P值最小,且小于0.05,是影響應力的顯著性因素,橡膠寬度的顯著性次之,橡膠硬度P值為0.94,遠大于0.05,是應力的非顯著性因素;在應變方面,橡膠硬度、厚度和寬度的P值遠遠小于0.05,三者均為彈性齒輪應變的顯著性影響因素。
3.3 橡膠參數水平優組合的確定
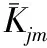
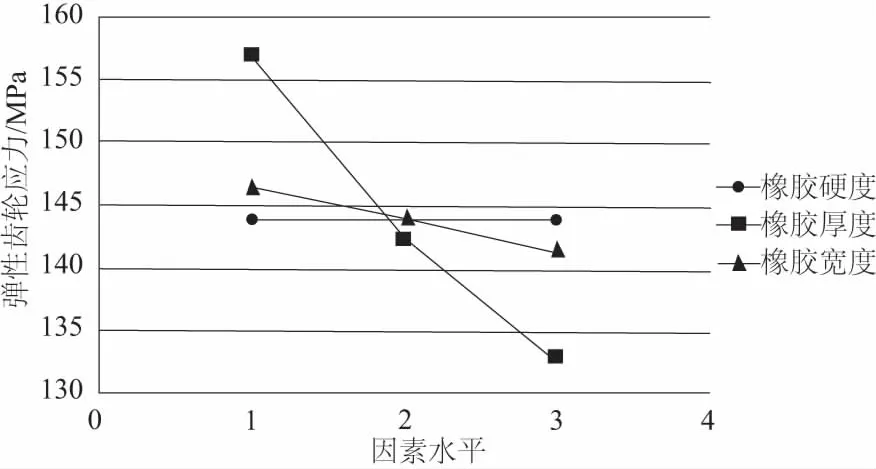
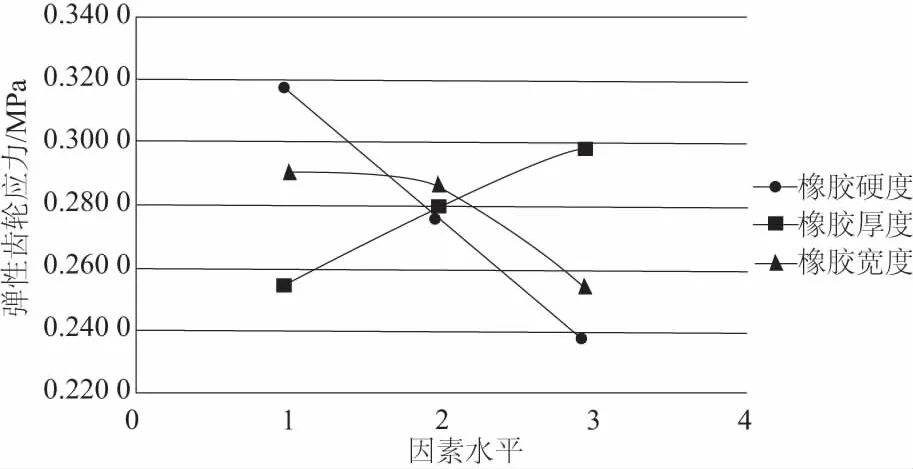
圖8 橡膠硬度、厚度和寬度與指標關系趨勢圖
由圖8可知,橡膠硬度增大,彈性齒輪應力幾乎不變,橡膠應變減小;橡膠厚度增大,彈性齒輪應力減小,橡膠應變增大;橡膠寬度增大,彈性齒輪應力減小,橡膠應變減小。經驗證,正交實驗得到的結論與單因素分析的結論具有一致性趨勢。
綜合考慮以確定橡膠厚度:橡膠厚度過大,在齒輪嚙合傳動中容易引起較大的軸向振動和變形,厚度太小,生產加工困難,質量控制成本過高。從安全性和經濟性方面綜合考慮,選取橡膠厚度優水平為3.5mm,此時,優水平組合為橡膠硬度HS70,橡膠厚度為3.5mm,橡膠寬度為13mm。
在工程實際中HNBR硬度最高可達HS75,根據圖8所示橡膠硬度對應力應變影響趨勢,從減小橡膠應變考慮,橡膠硬度的優水平為HS75。經驗證,該水平下的彈性齒輪應力為138.61MPa,應變為0.161 4mm,為最優標準。因此,橡膠參數的優組合為:橡膠硬度HS75,厚度為3.5mm,寬度為13mm。
4 結語
本文基于Pro/E建立了精確的彈性齒輪的參數化模型,對比了同工況下全金屬齒輪和彈性齒輪應力與應變情況,基于正交實驗設計方法分析了橡膠參數對齒輪應力與應變的影響,得出以下結論:1) 彈性齒輪能夠有效降低齒輪接觸應力,應力減小約24%;2) 橡膠硬度增大,彈性齒輪應力幾乎不變,橡膠應變減小;橡膠厚度增大,彈性齒輪應力減小,橡膠應變增大;橡膠寬度增大,彈性齒輪應力減小,橡膠應變減小;3) 彈性齒輪橡膠參數的優組合:橡膠硬度HS75,橡膠厚度為3.5 mm,橡膠寬度為13 mm。
由于目前條件限制,未能進行彈性齒輪的實驗驗證,有待后續完善。此外,橡膠參數對齒輪傳動系統動力學特性的影響有待進一步研究。

