債券市場投資中的非線性相關結構分析

范國斌 于翠婷 廖靜池

(1.西南財經大學統計學院，四川 成都 611130；2.西南石油大學經濟管理學院，四川 成都 610500；3.深圳證券交易所，廣東 深圳 518038)

引言

股市常常動蕩不安，即使進入21世紀以來，中國股市也已經歷了三次較大的危機：2000～2001年，國有股減持計劃導致股市大跌；2008年受全球金融危機影響，中國股市同樣經歷了很長時間的低迷；而從2015年下半年開始，股市再次遭受了迄今為止最為迅猛的熊市沖擊，2016年首日開盤施行“熔斷機制”，一日連續兩次觸發，直至今日股市仍在起伏。然而在股民深陷股市危機時，卻很少有人選擇投資其他市場進行風險分散化，尤其是成立已久的債券市場。Neftci等(2007)[8]指出中國股市散戶投資者占多數，他們更傾向于在股市和銀行存款之間調配自己資產，而很少同時參與股市和債市投資，債券市場上發揮主要角色的是機構類投資者。雖然由于經濟制度、監管體制等因素的影響，中國債券市場的發展落后于股市，但金融理論早已證實，債券是相比股票更為安全的資產。而且Barsky(1989)[1]研究表明，股市和債市在金融風險時期會體現為負相關關系。當股市重挫時，投資者會拋售股票而購買風險更低的債券，并把這種行為稱之為“安全投資轉移(Flight-to-quality)”。對于深受股市風險困擾的中國投資者，正在不斷發展和完善的債券市場能否成為其“避風港”？為此，本文試圖對中國股市和債市間關系進行全面而科學的分析，以考察中國債券市場是否能為股市投資者提供一個風險分散化渠道。

進一步，當投資者考慮進入債券市場時，還必須注意債市中有很多不同的債券：從交易場所上講有銀行間債券和交易所債券，從期限上講有長期債券和中短期債券，而從發行人上講有國債、企業債和金融債。不同類型的債券和股市的關系可能會有所不同，而且投資者同時持有這些不同債券類型時，這些不同類型債券之間的相關關系同樣值得考察。因此，除了股市與債市間關系外，本文也將對債市中不同類型債券間關系進行研究，從而幫助考慮進入債券市場的投資者制定合理的組合策略。

文獻綜述

對于股市和債市間關系，國外研究觀點并不一致：Underwood(2009)[12]發現股市和債市間傾向于呈現為負相關關系，但Sellin(2001)[11]研究卻認為，股票和債券會受到如貨幣政策等共同因素的影響而體現出正相關關系。然而后續的研究卻進一步發現，事實上股市和債市間關系在不同的狀態下會有所不同：Connolly等(2005)[2]發現，股市不確定性會導致股市與債市關聯性改變，當股票市場不確定性加劇時，股市和債市會呈現負相關關系，從而使得分散化持有股票和債券能獲得更大收益。Gonzalo和Olmo(2005)[4]也發現，當僅有股市面臨危機時，股市與債市間存在安全投資轉移行為，而當兩個市場同時面臨負沖擊時，股市與債市之間會具有傳染效應而體現為正相關。越來越多的研究表明，股市與債市間關系是會隨著時間變化的(Yang等，2009)[13]。對于中國股市和債市間關系，現有研究也無一致結論：同樣發現中國股市與債市間關系會隨時間而變化(袁超等，2008)[18]。

在中國債券市場中，因交易場所、發行人以及期限的不同，存在很多類型的債券。大量研究表明，這些不同類型的債券可能會具有不同特征(巴曙松與姚飛，2013)[14]。因此，在考察股市與債市間關系時，有必要考慮到不同類型的債券可能會與股市間具有不同相關關系模式。同時，當投資者同時持有多種類型的債券時，還應考慮不同債券類型間的相關關系。然而現有研究卻很少注意到這點，王璐和龐皓(2008)[16]曾分交易所和銀行間債券市場來考察股市與債市間關系，而鄭良海和侯英(2012)[19]曾考察了銀行間債券市場和交易所債券市場間動態關系。除此之外，金融市場上投資者會因投資目的不同而選擇不同的投資期限，所以無論考察股市與債市間關系時，還是考察不同債券類型間關系時，都有必要分不同頻率的收益率進行全面分析。但現有文獻中，只有閔曉平(2013)[15]曾經基于不同頻率的數據對公司債市場的流動性進行了分析。

另外在分析上述相關關系時，必須注意到無論是股市與債市間關系，還是不同類型債券間關系，均有可能體現出非線性特征。大量研究表明，不同金融市場或不同金融資產之間的相關結構往往是非線性的，存在尾部相關性特征，也即極端情形下收益間相關程度會高于正常情形。因此，Copula函數作為一種更為靈活的工具，被廣泛用來對這種非線性相關結構進行建模。Miller和Liu(2006)[7]等文獻指出忽略了這種非線性相關結構特征會給投資者的資產配置績效和組合風險管理帶來極大損失。而Rodriguez(2007)[10]和Okimoto(2008)[9]又進一步發現不同市場或不同資產間相關結構不僅是非線性的，還有可能隨時間變化。這一相關結構的時變性同樣會影響投資者的組合策略(Fan和Zeng，2012)[3]，但目前只有肖利平(2011)[17]曾使用SJC-Copula對中國股市和債市間相關結構的非線性特征進行了分析。

鑒于現有研究的缺陷，本文旨在以下方面做出貢獻。在研究角度方面：第一，鑒于現有研究對股市和債市之間的關系為正還是為負并無一致結論，本文考察中國股市和債市之間的關系究竟為何方向；第二，關于股市和債市間關系，存在不同理論。那么不同類型的債券便有可能體現出和股市不同的關系，而以往文獻并未分析這一可能，因此本文除了股市和債市整體關系之外，進一步分析不同類型的債券與股市間關系是否不同；第三，如果投資者同時持有不同類型的債券，那么這些不同類型債券之間的相關關系也對組合績效至關重要，因此本文還進一步考察不同類型債券之間的關系；第四，不同的投資者可能會選擇不同的投資期限，因此與以往文獻不同，本文基于三種不同頻率的數據(日收益、周收益和月收益)考察股市與債市間相關結構以及不同債券類型間相關結構，分析不同頻率下相關結構模式的可能不同。而在研究方法方面：使用靈活的Copula函數來對上述相關關系進行建模，以考察其相關結構是否具有非線性特征，并結合馬爾科夫轉換技術來進一步考察其非線性相關結構是否具有時變性。通過上述的科學分析，本文試圖為投資者選擇合理的債券產品構建其組合策略提供重要參考。

基于Copula的相關結構建模

一、Copula函數簡介

Copula是一種可以將聯合多元分布函數與各邊際分布函數聯系起來的連接函數。Copula理論中核心的Sklar’s定理指出：對于一個邊際分布函數為F1,...,Fn的聯合分布函數F，一定存在一個Copula函數使得F(x1,...,xn)=C(F1(x1),...,Fn(xn)),，其中邊際分布的信息包含在Fi(xi)中，而變量之間的相關結構完全由Copula函數來刻畫。這樣我們可以先對邊際分布做出任何假設，然后再選取不同的Copula函數來對相關結構單獨建模。Copula可以度量非線性的相關結構，與線性的方差協方差矩陣不同，Copula函數允許處于分布中間和分布尾部的相關程度有所不同。特別地，特定的Copula函數可以捕捉到不同資產收益率之間的尾部相關性，即不同資產價格同時暴漲和暴跌的可能性大小。

不同的Copula函數代表著不同的相關結構模式，也對應有不同的尾部相關特征。本文首先選用文獻中常用的4種Copula函數類型：Gaussian、T、Clayton和Gumbel。其中Gaussian Copula不存在尾部相關性(即不同資產價格暴漲或暴跌的情況是相互獨立的)，常被作為基準模型使用；T Copula同時具有上尾和下尾相關性(即不同資產的價格既會同時暴漲又會同時暴跌)；不過這兩種Copula函數所刻畫的相關結構是對稱的，而Clayton 和Gumbel Copula雖然可以度量非對稱的相關結構，但前者只存在下尾相關性(即不同資產的價格僅可能同時暴跌但不會同時暴漲)，后者只存在上尾相關性(即不同資產的價格僅可能同時暴漲但不會同時暴跌)。

金融資產間的相關結構事實上是相當復雜的，有時很難用單一的Copula函數來進行刻畫。當市場處于暴漲或暴跌時期，資產間相關性都會明顯增強。而Clayton和Gumbel Copula只能捕捉到在下尾或下尾處一側的尾部相關性，T Copula雖然在上尾和下尾處兩側都具有尾部相關性，但是其尾部相關性是對稱的。可是在牛市和熊市時期的資產間相關性往往是非對稱的，為了全面刻畫股票與債券間以及不同債券間的相關結構，引入Hu(2006)[6]所提出的混合Copula的概念，構建一個Clayton和Gumbel Copula的線性組合。具體如下：

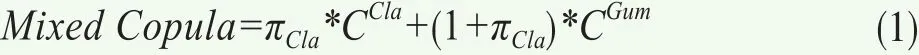
其中CCla和CGum分別指Clayton和Gumbel Copula函數，而πCla和πGum指這兩種Copula函數對應的權重。這樣構建的混合Copula相對比較靈活，同時存在上尾和下尾相關性，而且在上尾和下尾處兩側的尾部相關性程度是非對稱的。首先同時使用單一Copula函數和混合Copula對靜態相關結構進行全面的分析，然后進一步引入馬爾可夫轉換模型來考察相關結構的時變性。

二、馬爾可夫轉換模型的引入

為了考察資產間相關結構是否會在不同的時期有所不同，參照Rodriguez(2007)[10]和Okimoto(2008)[9]的做法，本文同樣將Copula函數與馬爾可夫模型結合起來對相關結構進行建模。首先，嘗試令不同資產間的相關結構服從一個兩狀態馬爾可夫轉換過程，在不同的狀態下，相關結構由不同的Copula函數來刻畫，具體設定如下：

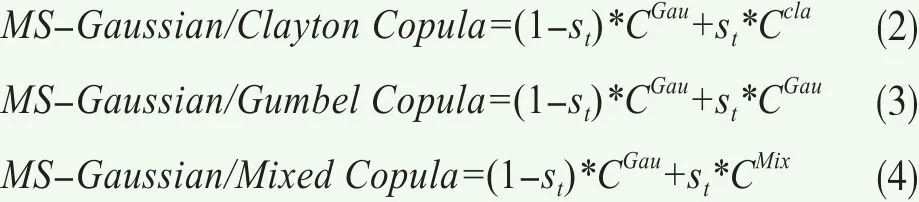
其中Ci,i∈{Gau,Cla,Gum,Mix}分別指前文給出的各類單一Copula函數以及混合Copula。由于在市場暴跌或暴漲時期，不同市場或不同資產之間的相關程度可能會變得比市場平靜時期更強，因此在上述3種馬爾可夫轉換Copula設定中，均將市場狀態設置為兩狀態。其中狀態一為市場平靜狀態(st=0)，此時變量間相關結構由不存在尾部相關性的Gaussian Copula來刻畫；而狀態二為市場動蕩狀態(st=1)，此時變量間相關結構由Clayton、Gumbel 或混合Copula來刻畫，這三種非對稱的Copula來刻畫均能夠捕捉在市場暴跌或暴漲時可能出現的非對稱尾部相關性特征。除此之外，本文還嘗試引入了第四種設定“MS-T Copula”，允許T Copula的自由度參數依狀態進行轉換。與前面三種設定類似地，將市場狀態設置為兩狀態，狀態一((st=0))和狀態二((st=01)分別對應市場平靜時期和市場動蕩時期。其中在狀態一下，T Copula的自由度參數變大，從而使得T Copula事實上已經退化為Gaussian Copula，尾部相關性會變得消失；在狀態二下，T Copula的自由度參數相對較小，因此可以捕捉市場暴跌或暴漲時可能出現的尾部相關性特征。在四種不同的設定中，均令狀態 的變化服從一個馬爾可夫鏈，其狀態轉移矩陣為

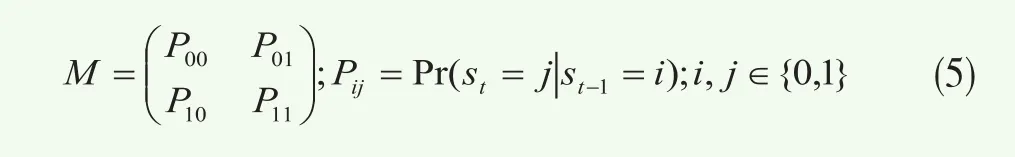
這種將馬爾可夫轉換和Copula函數結合起來研究資產間相關結構的方法可以使得不同的時期相關結構發生變化，而不僅僅是同一種相關結構的相關程度的變化，本文把這種方法稱之為“馬爾可夫轉換Copula”。

對于馬爾可夫轉換Copula模型的估計，首先在每一時刻t可以計算得到基于不同狀態和以往收益的條件密度函數：

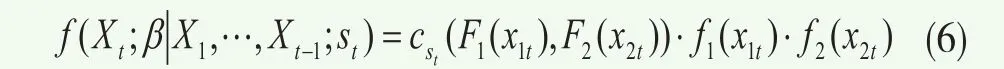
其中 為在時刻t的觀測值，β表示需要估計的參數，cs所對應的Copula函數類型取決于不可觀測的狀態st。然后可以按照Hamilton(1994)[5]給出的循環程序得到不再依賴于狀態的無條件密度函數，并最后寫出似然函數:試公式(2)～(4)所設定的三種馬爾科夫轉換Copula形式；如果最優Copula函數為對稱的T Copula，那么嘗試第四種馬爾科夫轉換Copula形式“MS-T Copula”。通過對比馬爾科夫轉換Copula形式與靜態Copula的AIC值，以及觀察馬爾科夫轉換Copula形式下相關結構是否會在不同狀態下有所不同，從而分析上述相關結構是否會存在時變性特征。

實證結果與分析

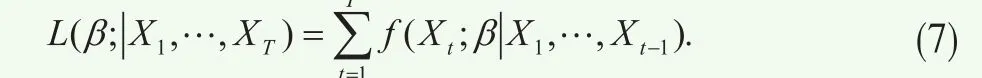
得到上面的似然函數之后，采用極大似然估計就可以得到模型參數值。

基于以上方法，本文對股票和債券間相關結構以及不同債券間相關結構進行分析，并將所有資產的邊際分布均設定為經驗分布形式。首先根據AIC準則選取最優的靜態Copula函數類型，然后基于最優Copula函數進一步考察可能的時變性特征：如果最優Copula函數為非對稱的Copula類型(Clayton、Gumbel或Mixed Copula)，那么嘗

為了考察股市和債市之間的相關結構，本文搜集了上證綜合指數、深證成份股指數和中債總指數，樣本區間為2012年1月4日～2015年12月31日。除了股市和債市間整體關系的分析外，進一步搜集了債券市場上不同類型債券指數的數據：交易所債券與銀行間債券指數(按交易場所不同)，中短期債券與長期債券指數(按償還期限不同)，國債、企業債和金融債指數(按發行人不同)。進而，分析上述每一類型債券與股市間的相關結構以及不同債券類型之間的相關結構，由于分類債券指數數據起始日期較晚，因此涉及到分類債券指數的相關結構分析樣本區間為2006年11月21日～2015年12月31日。本文分別計算了上述指數的日收益、周收益和月收益，對比分析不同頻率下的相關結構特征，所有收益率均基于收盤價計算為對數收益率。

一、股市與債市間相關結構

由于股市和債市間關系為正還是為負并不明確，因此在考察兩者關系時，分別嘗試了對股票收益率與債券收益率直接進行Copula建模和對股票收益率和債券收益率的相反數間關系進行Copula建模，對比其AIC值發現，后者擬合程度明顯更高。因此，本文選擇將股票收益率和債券收益率的相反數間相關結構的估計結果以表1～3給出，其中符號為正的相關系數(ρ)或尾部相關系數(λU和λL分別代表上尾和下尾相關性系數)代表著股市和債市間存在負向關系。除了股市和整個債市間相關結構外，還給出了股票和不同類型債券間的相關結構，表1～3分別為基于日收益、周收益和月收益的結果。從中可以看出：

首先，雖然對于日收益率，股市和債市間相關關系較弱，但對于周收益和月收益，無論是股市和整個債市間還是股市和不同分類債券間，均存在不可忽略的負相關關系，而且頻率越低，負相關程度越強。這至少對于投資期限較長的投資者來說是個好消息，股票和債券之間的負相關關系意味著中國債券市場確實能夠對股市風險起到一定的分散化作用。這一發現也可能表明中國金融市場上也存在一定的“安全投資轉移”現象，即在股市風險較大時，投資者會轉而購買風險更低的債券，從而使得股市和債市體現出一定的負相關關系。只是因為通常投資者調整其資產組合的頻率相對較低，所以這種負相關關系只在周收益和月收益間體現，而在日收益間并不明顯。

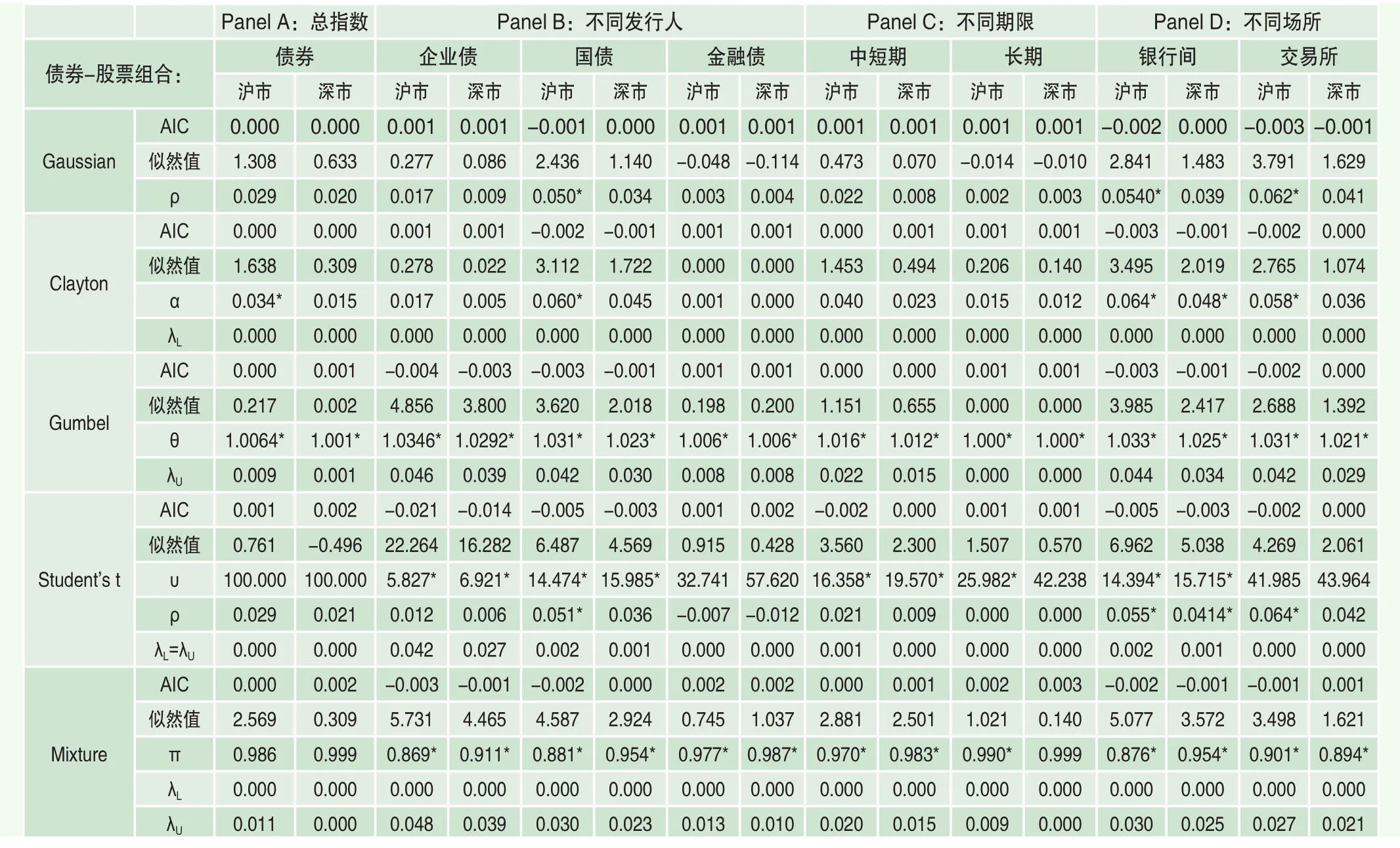
表1 基于日收益的中國股市與債市間相關結構分析

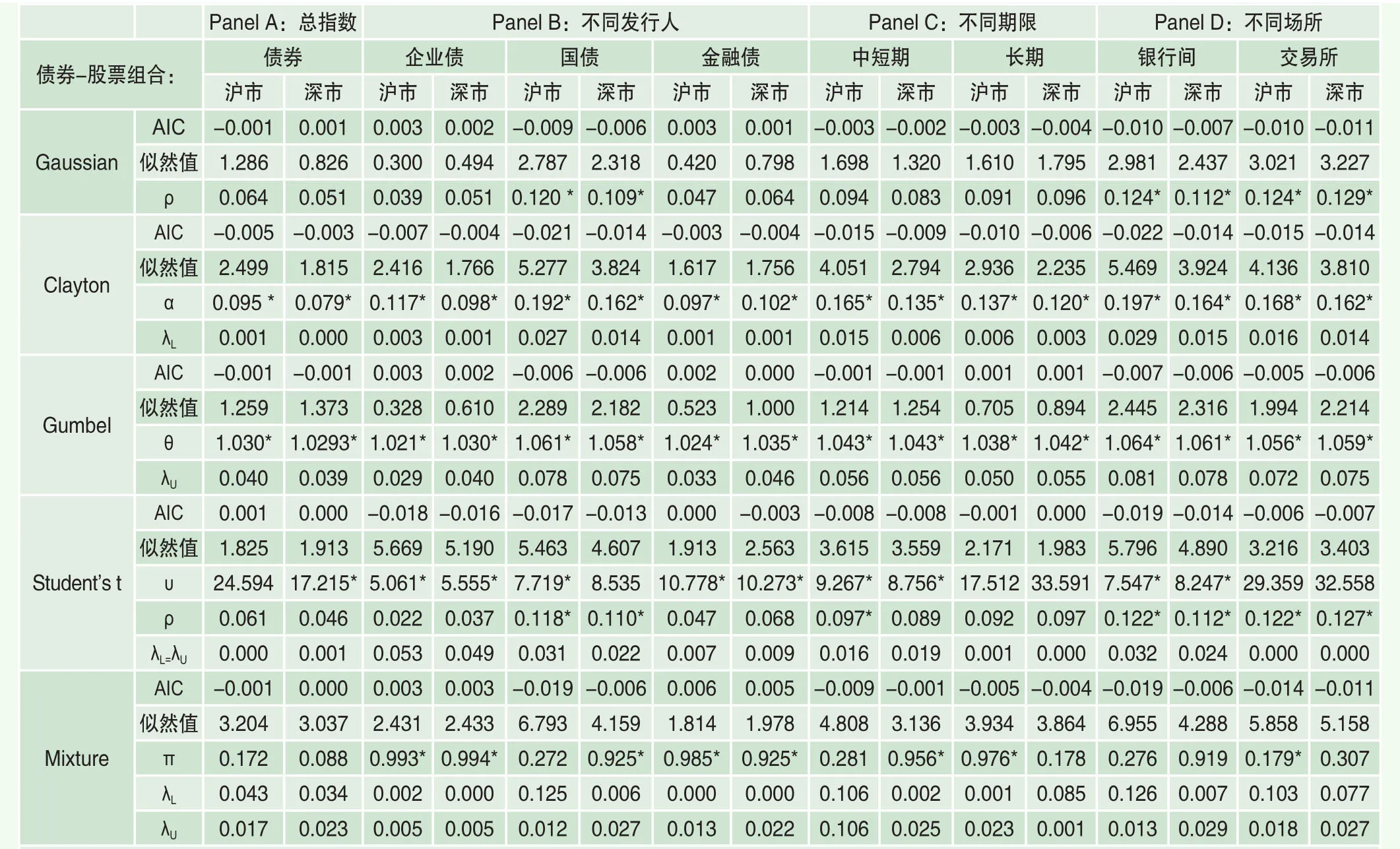
表2 基于周收益的中國股市與債市間相關結構分析

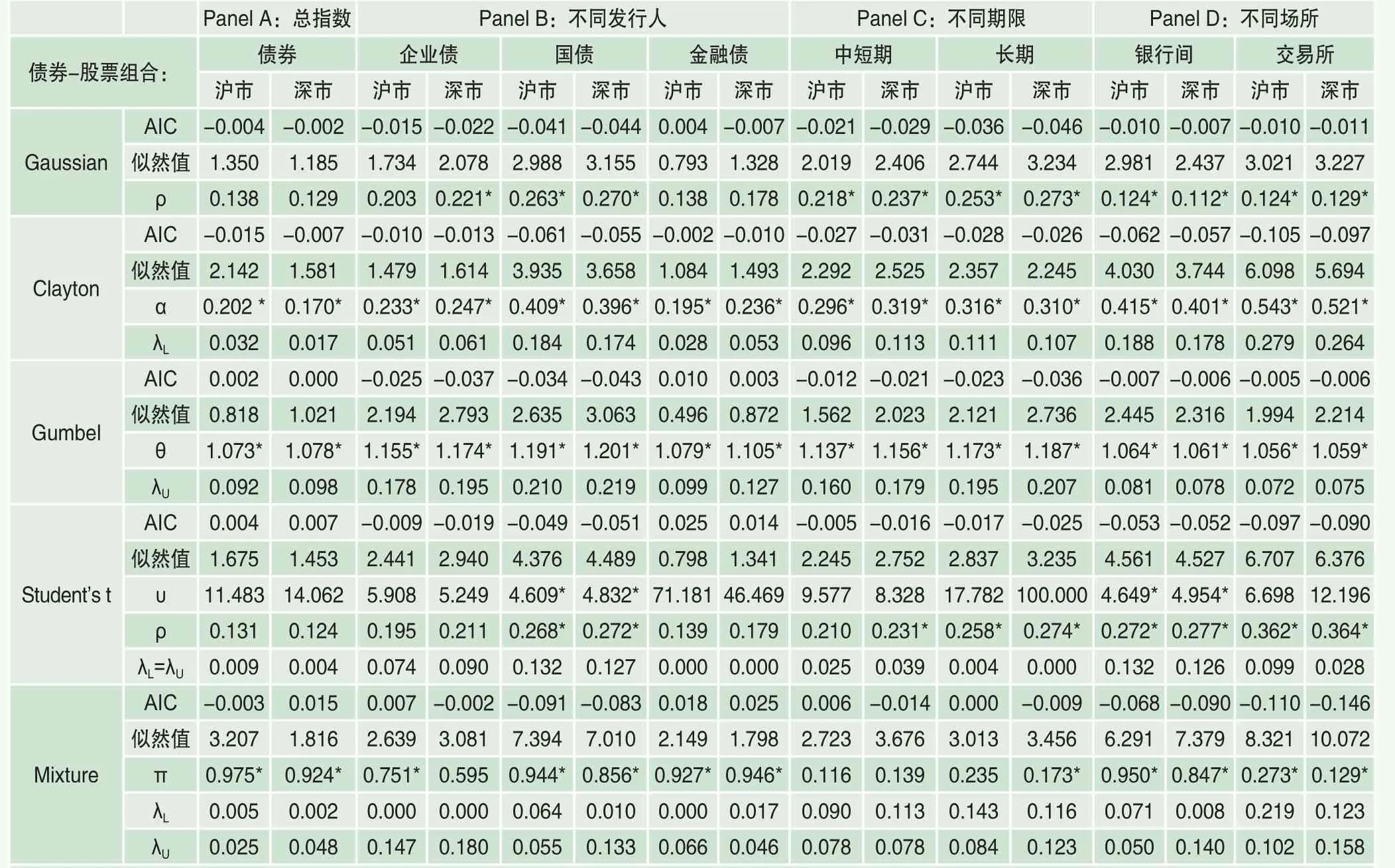
表3 基于月收益的中國股市與債市間相關結構分析

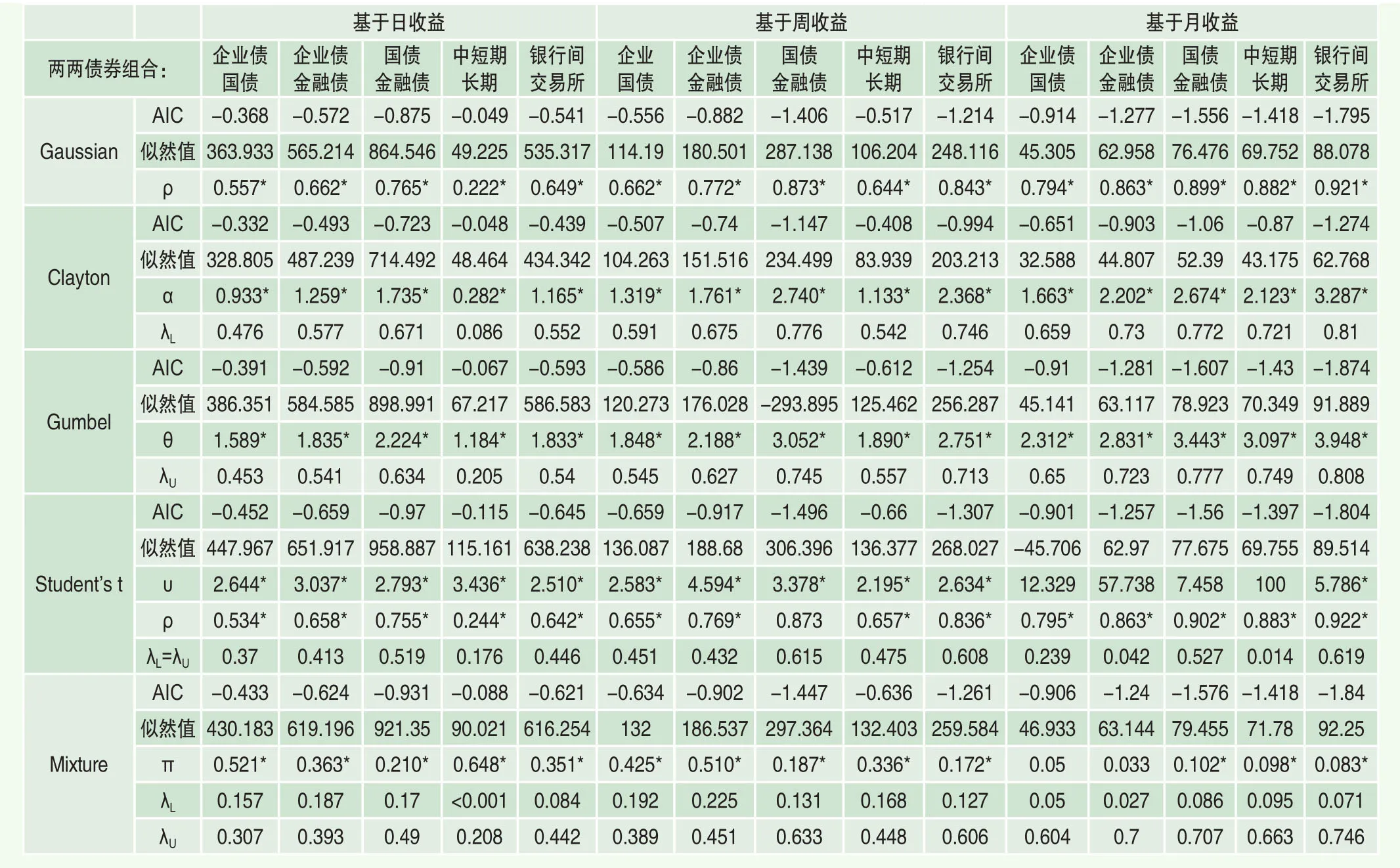
表4 不同類型債券間相關結構分析

而且，不同頻率下的相關結構均明顯體現出尾部相關性特征，刻畫日收益間相關結構的最優類型為T Copula，刻畫周收益間相關結構的最優類型為Clayton Copula，而刻畫月收益間相關結構的最優類型為Clayton Copula或Mixed Copula。前文已指出，這種尾部相關性特征意味著，當市場處于暴漲或暴跌時期，兩項資產之間的相關程度會變得相對更強。而且三種頻率下的最優Copula函數類型均具有下尾相關性，對于本文來說，下尾對應于股市收益率下降的時候。也就是說，當股市收益率下降時，股市和債市間負相關程度會更強，這提示我們，在股市暴跌時期，債券市場對股市風險的對沖作用更為明顯。

進一步對比不同類型債券與股票間相關關系則顯示，在發行人不同的債券中，企業債和股市的相關程度最強，三種頻率下結果均如此；在償付期限不同的債券中，對于日收益和周收益，中短期債券與股市間相關程度更高，而對于月收益，長期債券與股市間相關程度更強；在交易場所不同的債券中，銀行間債券和交易所債券與股市間的相關程度并無一致結論。此外，對比滬市和深市兩個市場與債券間相關程度時表明，對于日收益和周收益，滬市體現出更強的與債市間相關關系，然而對于月收益，深市與債市間相關程度卻強于滬市。

二、不同類型債券間相關結構

當投資者進入債券市場時，有多種不同類型的債券可供其選擇，而不同類型債券間的相關結構也對其組合策略至關重要。因此，本文對三種劃分準則下的不同債券間的兩兩相關結構進行分析，并將估計結果在表4中給出。與表1～3的結果不同，此處是對兩種債券的收益率間關系直接進行Copula建模(并未取相反數)。首先，從結果中可以看出：與股市和債市間相對較弱的負相關關系不同，不同債券之間表現出很強的正相關關系，而且隨著頻率降低，不同債券之間的正向相關程度越來越強。這意味著，當在一個組合中同時持有多種債券類型時，必須注意其收益率會更傾向于同向變化而很難發揮風險分散化的作用。而且，三種頻率下的相關結構均存在著明顯的尾部相關性特征，也就是說，對于不同債券類型間關系，也會同樣在市場暴漲或暴跌時表現出相比平靜時期更強的相關程度，因此使得我們在最需要分散風險的時候卻很難通過持有不同債券類型來實現目的。

對比不同頻率下結果可以發現，對于日收益和周收益來說，刻畫不同類型債券間相關結構最優的函數是T Copula，說明同時存在著對稱的上尾和下尾相關性，也即無論在市場暴漲還是暴跌時期，不同債券的收益率相關性均會有所增加。而對于月收益來說，刻畫不同類型債券間相關結構最優的函數是Gumbel Copula，該函數僅存在有上尾相關性。這意味著，對于持有債券期限較長的投資者來說，不同類型債券的收益率更傾向于在市場好轉的時候體現出更高的相關程度。

三、相關結構的時變性特征

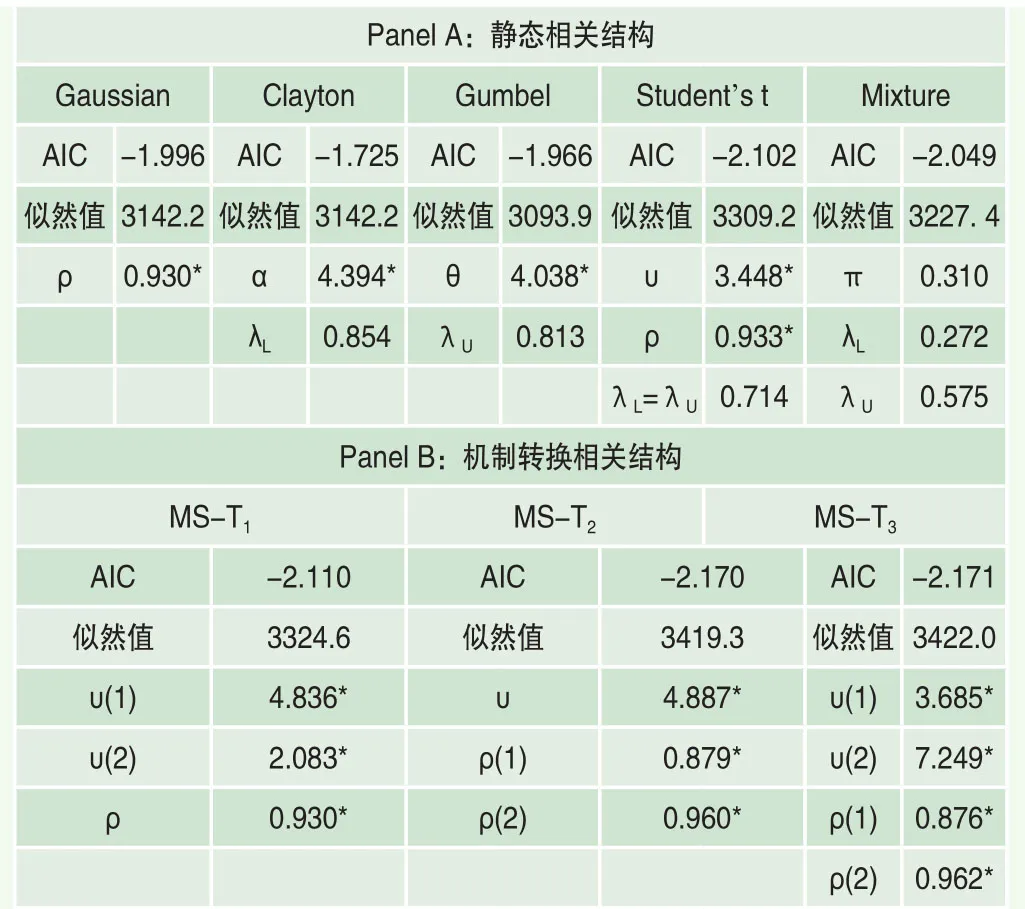
表5 滬深兩市間相關結構及其時變性特征分析(基于日收益)

大量文獻表明，金融市場或金融資產間相關結構不僅是非線性的，而且還有可能是時變的。如果對滬深兩個股市間相關結構進行分析，可以發現雖然其靜態相關結構最優的仍然為T Copula，但進一步引入馬爾科夫轉換機制后發現，其相關結構會隨時間發生明顯變化。由于最優的靜態相關結構為T Copula，所以選擇第四種馬爾科夫轉換Copula設定形式“MS-T Copula”，分別嘗試只讓T Copula的自由度參數依機制轉換、只讓T Copula的相關系數參數依機制轉換、讓T Copula的自由度參數和相關系數參數同時依機制轉換，在表5中將其標記為“MST1”，“MS-T2”和“MS-T3”。基于AIC準則對比發現，馬爾科夫轉換Copula設定的擬合程度明顯優于靜態Copula，其中最優形式“MS-T3”的參數估計結果顯示，兩個股市間的相關系數和自由度參數會在不同狀態下有所不同。

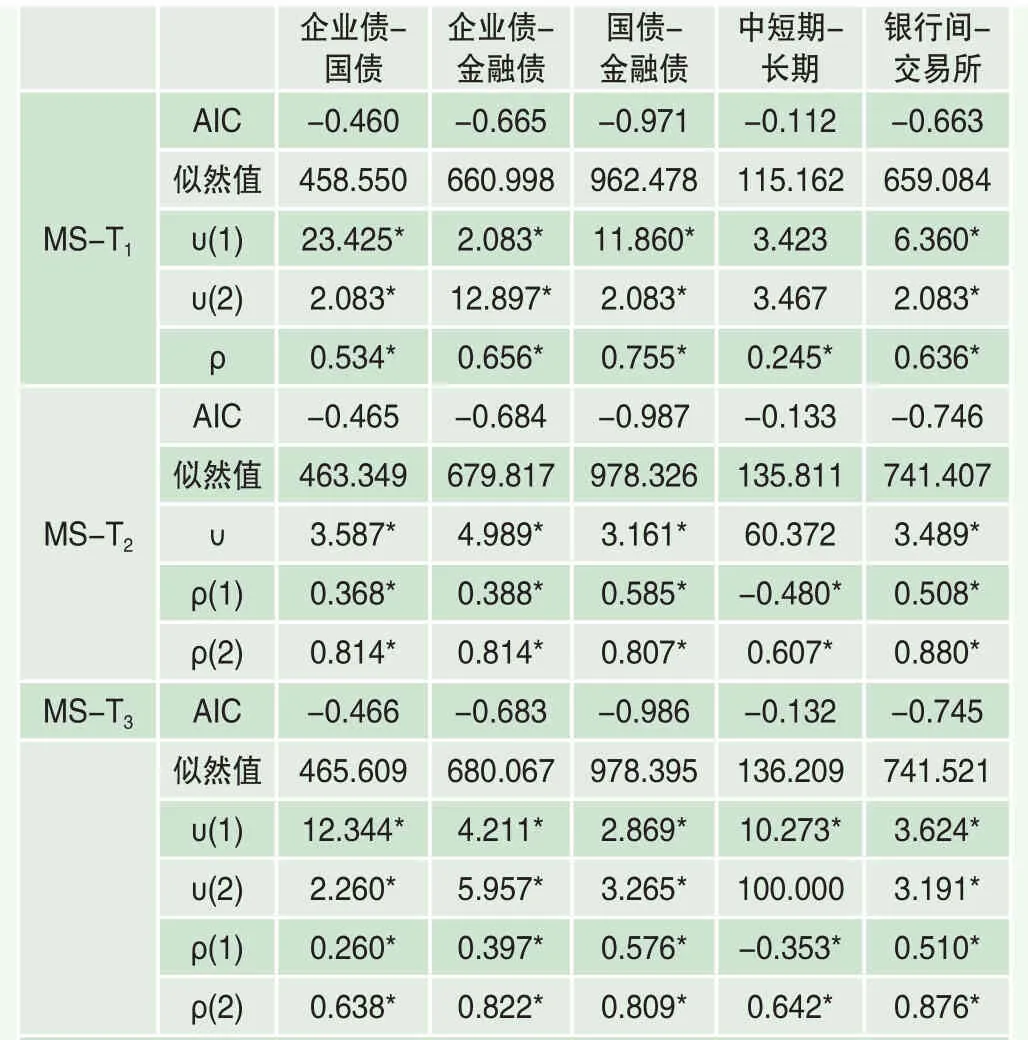
表6 不同類型債券間相關結構的時變性特征分析(基于日收益)

因此，對于股市和債市之間相關結構以及不同類型債券之間的相關結構，同樣有必要進一步引入馬爾科夫轉換技術考察其相關結構可能的時變性。對于股市和債市間相關結構，可能因為其相關程度較弱，嘗試了本文所設定的四種不同馬爾科夫轉換Copula形式，均未發現存在時變性特征。然而對于債券市場上不同類型的債券之間相關結構，卻可以發現存在明顯的時變性特征。由于表4結果顯示，不同類型債券之間最優的靜態相關結構T Copula，所以同樣選擇“MS-T Copula”的設定形式，與表5中結果類似，分別嘗試了“MS-T1”，“MS-T2”和“MS-T3”三種情況。同樣地，表6的結果告訴我們，馬爾科夫轉換Copula設定形式的擬合程度明顯優于靜態Copula，其中最優的形式為“MS-T2”。也就是說，不同類型債券間相關結構具有時變性特征，其相關系數會在不同狀態下有所不同。

結論

隨著中國金融市場的不斷健全和完善，投資者應該與時俱進，不再只局限于股市，而應該考慮投資于不同市場以主動進行風險分散化。尤其是當股市風險較大的時候，應考慮選擇相對更為安全的資產，例如債券。然而，債市究竟能否成為股市的“避風港”以及投資于債市時應選擇哪些類型的債券？為回答這些問題，本文對中國股市與債市間和債市中不同類型債券間非線性相關結構進行了全面分析，并得到如下結論：中國債券市場能夠為股市提供一定的風險對沖作用，尤其是對于周收益和月收益，債市和股市間存在較強的負相關關系。這說明至少對于投資期限較長的投資者來說，可以通過持有債券來分散化股市風險；在不同類型的債券中，企業債和股市間的負相關關系相對較強，因此企業債可能是對沖股市風險的最佳選擇；其他債券類型和股市間關系強弱程度則無明顯差異，而且債市中不同類型債券間關系顯著為正，因此投資者在考慮持有債券時，沒有必要同時持有多種不同類型的債券，可能并不會為風險分散化帶來進一步的幫助；此外，債市和股市間相關結構具有明顯的尾部相關性特征，也即在股市下跌時，兩者間負相關程度更強，因此同時持有股票和債券的風險分散化效果將更為明顯；最后，債市中不同類型債券間相關結構不僅同樣為非線性，而且還會進一步體現出時變性特征。具體而言，在市場動蕩狀態下，不同債券之間會表現出明顯的尾部相關性，其正向相關關系的程度將變得更強。這再次提示投資者，在試圖通過持有債券來對沖股市風險時，選擇同時持有多種債券的意義不大。

所有這些結論對于試圖進入債券市場的投資者來說具有重要參考價值：首先，這意味著投資者確實可以選擇通過債市來分散股市風險。但是，同時持有多種不同類型債券時卻要注意它們之間的收益往往會同向變化，要合理控制自己的組合風險。另外，股市和債市間相關結構和不同類型債券間相關結構均具有非線性特征，而且不同類型債券間相關結構還進一步具有時變性特征，考慮到這兩種特征將能給投資者的資產配置績效和組合風險管理帶來明顯的改進。