基于改進FWA-NN的污水處理過程溶解氧濃度預測

陳如清,俞金壽

?

基于改進FWA-NN的污水處理過程溶解氧濃度預測

陳如清1*,俞金壽2

(1.嘉興學院機電工程學院,浙江 嘉興 314001；2.華東理工大學自動化研究所,上海 200237)

為實現對污水處理過程溶解氧質量濃度的實時準確預測,提出了一種改進的混沌煙花混合優化算法并構建了基于改進算法的神經網絡在線軟測量模型.結合污水處理過程的數據特征,定義了一項新的樣本相似度衡量指標用于提取更具代表性的建模數據.在改進算法中,為提高基本煙花算法初始成員的質量,定義了一種改進的兩級正弦混沌映射并利用混沌運動的遍歷性精選煙花算法的初始群成員;通過融合混沌算法改進了基本煙花算法的搜索機制,基于設定準則將尋優過程分為兩階段并采用兩分群同時進行.測試結果表明改進算法的收斂速度和收斂精度有較大程度提高.將改進的軟測量建模方法和樣本數據提取方法用于污水處理過程溶解氧質量濃度軟測量建模,應用結果表明該模型的均方根誤差和平均泛化誤差分別為0.0175和0.0118,具有較強的泛化性能.

污水處理過程；溶解氧質量濃度；軟測量建模；煙花算法；相似度衡量

城鎮污水處理及再生利用是改善生態環境、解決城市缺水問題的有效途徑之一[1-2].目前污水處理多采用生化法,是工業和城市污水處理的最主要途徑.污水處理生化反應過程中溶解氧濃度(DO)是一項重要指標,能及時反應整個污水處理系統的運行狀況,DO的監測與控制對提高污水處理過程的處理質量和處理效率至關重要[3-4].實際污水處理過程具有污水成分繁雜多變、污水污泥流量存在較大不確定性等特征,DO等參數的在線軟測量技術研究具有重要意義[5-7].

人工神經網絡是一種常用的軟測量建模方法[8-9].為進一步提高神經網絡軟測量模型的性能,常將PSO等群體智能優化算法用于神經網絡的網絡權值優化.自2000年以來,諸多新型群體智能優化算法不斷涌現.例如根據煙花爆炸產生火花這一現象提出煙花算法(FWA),憑借其較強的尋優性能受到不同領域學者的廣泛關注[10-11].眾多學者從不同角度提出許多改進算法,用于解決神經網絡權值的訓練、連續和離散系統的參數優化及組合優化問題的求解等[12-15].此外,針對大數據或超大數據背景下的復雜優化問題,如電網覆冰災害預測[16]和Web服務組合優化[17]等,基于煙花算法也有較好的解決方案,應用結果表明將其用于大數據的分析處理是可行有效的.煙花算法屬于有導向的隨機性啟發式算法,在處理某些復雜優化問題時存在易陷入局部最優、進化后期收斂速度慢及魯棒性較差等不足.

為提高FWA初始煙花成員的質量,定義了一種改進的兩級正弦混沌映射并利用混沌運動的遍歷性在解空間產生較大規模的初始群體,按照各成員間的歐式距離從中提取分布均勻的FWA初始煙花,使有限規模的煙花均勻分布于解空間;為提高基本FWA的優化性能,融合混沌優化算法(COA)和FWA算法,提出了一種混沌煙花混合優化算法.整個優化過程分為兩階段,兩分群分別采用COA策略和FWA策略同時進行.對多個復雜多維函數的尋優測試結果表明,改進算法有效增強了種群中成員間的信息交流與共享、提高了種群的多樣性、擴大了在解空間的搜索范圍,避免了算法的早熟收斂.針對污水生化處理過程DO的軟測量建模問題,定義了一項新的樣本相似度衡量指標用于提取更具代表性的建模數據,并將改進算法用于軟測量建模中神經網絡的訓練,取得了良好的應用效果.

1 研究方法

1.1 基本煙花算法

基本煙花算法的實現思路是將煙花視為最優化問題解空間中的一個可行解,煙花爆炸產生一定數量火花的過程即為鄰域搜索最優解的過程.算法具體描述如下:

(1)隨機產生個煙花,即隨機在求解空間初始化個位置x,表征問題的個初始解.

(2)計算每個煙花的適應度值,評估煙花質量好壞并在不同爆炸半徑下產生不同數量的火花.煙花x的爆炸半徑R和爆炸火花數S的計算公式分別為:

式中:min=min((x))(=1,2,…,)為當前煙花種群中適應度最小值(最優值);max=max((x)) (=1, 2,…,)為當前煙花種群中適應度最大值(最差值).常數和分別用來調節爆炸半徑和產生爆炸火花數的大小,為用來避免除零運算的微小量.此外,為限制適應度值較好和適應度值較差的煙花位置產生火花粒子的數量,對火花產生個數作如下限制,即:

式中:、為兩個常數,round為四舍五入取整函數.

(3)產生爆炸火花,隨機選擇個維度組成集合DS,=round(′rand(0,1)),其中表示煙花x維數; round為四舍五入取整函數,rand為在區間內產生服從均勻分布隨機數的函數.參照式(4)對DS的各維度進行爆炸操作,越界處理后將ex保存于爆炸火花種群.

ex=x+,=R′rand(-1,1) (4)

式中:代表位置偏移量;x代表第個煙花個體的第維,ex代表x經爆炸操作后的爆炸火花.

(4)產生個高斯變異火花,隨機選擇火花x并隨機抽取個維度組成集合DS,令=round(′rand(0,1)),其中表示煙花成員x的維數.參照式(5)對DS的各維度作高斯變異運算,越界處理后將mx保存于高斯變異火花種群.

mx=x′(5)

式中:~(1,1),mx為x高斯變異后產生的高斯變異火花.

(5)從煙花、爆炸火花和高斯變異火花3類種群成員中精選個成員構成下一次迭代運算的煙花種群.設候選者集合為(包括3類種群成員),煙花種群規模為.中適應度值最優的個體首先被確定為下一代煙花成員,其余-1個煙花成員則通過輪盤賭方式依次從中選擇產生,候選者x被選中的概率為:

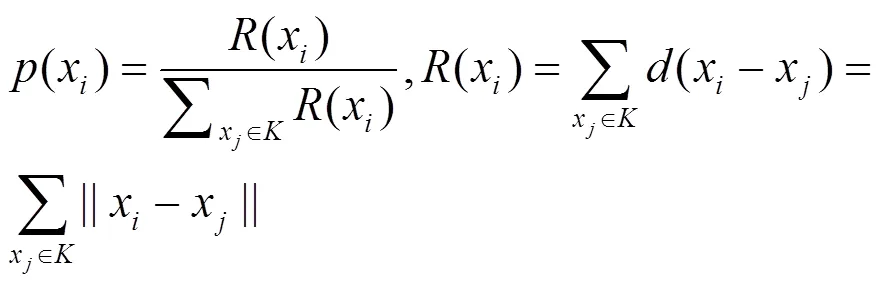
式中:(x)為x與中各個體間的距離和.中個體的密度越高則被選擇的概率越低.

(6)判定是否滿足終止條件.若滿足則停止搜索,否則返回步驟(2).

1.2 初始煙花成員的選取

根據基本FWA尋優機制,初始煙花成員的位置應均勻分布于整個解空間以增加尋找全局最優解的概率,故煙花成員的規模越大越有利,但同時也會增加算法的計算復雜度,根據求解問題的復雜程度不同群體規模通常設置為10~100個.常規FWA采用隨機方式選取初始煙花成員存在一定盲目性,當解空間范圍較大時難以確保有限數量煙花成員在整個解空間均勻遍布,加大了FWA算法陷于局部最優的概率,不利于提高算法的整體優化效率.

混沌現象指的是一種確定的但不可預測的運動狀態,運動遍歷特性可使混沌變量按其自身“規律”在一定范圍內不重復地遍歷所有狀態.如式(7)所示,Logistic映射是研究混沌運動的一種經典模型,在＝4的情況下處于完全混沌狀態.

+1=(1-) (7)

分析研究表明由式(7)所產生的混沌變量軌道點分布并不均勻,存在不動點(即多次迭代趨近某個固定值)和穩定窗(即點聚集某個區間)問題[18].文獻[19]定義了一種正弦混沌映射,仿真表明其遍歷性優于Logistic映射.針以上問題,本文在現有方法基礎上采用兩級正弦混沌映射,對分形系數進行重新分配,定義一種改進的正弦混沌映射SM:

+2=sin(5.65/+1)+ (1-)sin(5.65/),-1￡￡1,0 (8)

式中:分形系數(0,1),當=0或=1時,該映射轉化為正弦混沌滿映射.此外,迭代的初始值0不能為0,且0不能取為無窮多個平衡點的任何一點,否則不能產生混沌.為使該混沌映射既能達到接近滿映射狀態,又能克服不動點與穩定窗的問題,一般取值接近0或1.仿真表明當=0.005時,其隨機性基本接近滿映射,混沌特性良好,故本文取=0.005.

為提高FWA初始煙花的質量,利用式(8)所定義的SM混沌映射在解空間產生較大規模的初始群體,根據成員間的歐式距離從中提取分布均勻的FWA初始煙花,使有限規模的煙花成員均勻遍布解空間.FWA初始煙花成員的選取過程描述如下:

1.3 混沌煙花混合優化算法

1.3.1 算法原理 常規FWA算法在搜索全局最優解的過程中,若遇到局部極值點易導致算法過早收斂而陷入局部最優.為提高FWA的整體優化性能,考慮將尋優過程分為2個階段:搜索初期盡量保持較快收斂速度并防止煙花成員的“早熟收斂”,引導煙花成員進行新區域的探索并盡可能遍歷至整個問題空間;搜索后期FWA達到一定收斂精度,若煙花成員陷入局部最優則采用替換部分煙花種群成員或重新調整算法參數的方式,迫使煙花成員逃離局部最優區以進一步提高FWA的收斂精度.

COA算法憑借混沌運動的遍歷性、隨機性和規律性,較現有直接搜索算法更容易跳出局部最優區,是一種很好的搜索機制;FWA具有原理簡單、搜索能力強,局部和全局搜索能力自調節機制等特點.本文將兩種搜索機制有機融合,根據群成員的不同搜索方式將整個尋優群體分為兩部分,分別命名為FWA分群(F群)和COA分群(C群).

優化過程分兩個階段進行:階段一,F群和C群分別按FWA機制和COA機制迭代.其中F群在計算煙花爆炸半徑R和爆炸火花數S時,式(1)和式(2)中min和max分別為時刻整個尋優群體(包含F群和C群)的適應度最優值和最差值.利用COA的全局遍歷性避免群成員“早熟”,并實現整個尋優過程中F群和C群的信息共享;階段二,當F群煙花成員陷入局部最優,C群成員則在以局部極值點為中心的附近區域內迭代,并將本分群適應值較好的部分成員取代F群中相同數量的較差成員,幫助F群成員遠離局部最優區.

1.3.2 算法步驟 設min(t)、max(t)分別代表時刻F群適應度最優值和最差值,min(t)、max(t)分別代表時刻C群適應度最優值和最差值,min和max分別代表時刻整群的適應度最優值和最差值.混沌FWA混合優化算法的執行流程為:

根據上文所述FWA初始煙花成員的選取方法,初始化兩分群成員的位置,完成分群規模、最大搜索次數max、尋優精度、FWA和COA相關參數的初始設置,計算全體群成員的初始適應值并記錄整群適應度最優值、最差值及對應的空間位置;

階段一,包括:1) F群成員按(1)~(6)式在解空間進行搜索,每次迭代產生成員新位置并計算新適應值,更新min()、max()及其空間位置;2) C群按式(8)產生新的混沌向量并進行線性變換,每次迭代產生成員新位置并計算新適應值,記錄min()、max()及其空間位置;3)比較min()、max()和min()、max()適應值大小,更新min、max及對應的空間位置;4)重復1)~3)步,尋優精度達到要求轉至階段三,若F群成員陷入局部最優(如全局歷史最優適應值在10~15次迭代內保持不變或無明顯變化),則進入階段二.

階段二,包括:1) 根據式(8)再次產生C群的個混沌向量(＝1,2,…,),參照式(9)在以min(t)對應的空間位置x()為中心及為半徑的鄰域內進行混沌搜索.

X＝*() +Y,＝1,2,…,(9)

式中:X表示求解空間成員的位置,F群成員位置和適應值更新方法與階段一相同;2) 計算兩分群各成員適應值并按適應值優劣進行排序,將F群的適應值較差成員用C群的適應值較好成員代替;3) 比較min(t)、max(t)和min(t)、max(t)適應值大小,保存min、max及對應的空間位置;4) 逐步縮小半徑并重復1)~3)步,精度要求滿足或最大迭代次數達到則轉至階段三.

階段三,停止搜索,輸出整群歷史最優解及相應的最優適應值.

1.3.3 性能測試 為驗證本文所提出的改進混合算法的有效性,進行了仿真實驗.實驗過程中引入基本PSO、GA和FWA3種優化算法與改進的混沌煙花混合優化算法(CFWA)進行對比.尋優測試對象為多峰值、多局部極值點且自變量之間相互獨立或互相影響的4個經典函數(Ackley、Rastrigrin、Griewank和Rosenbrock).其中,1()~3()函數的全局最小值為0,對應最優解為x=(0,0,…,0);4() 函數的全局最小值也為0,對應最優解為x=(1,1,…,1)時.4個經典函數在低維(如2~3維)情況下,由于局部極值點較少,常規PSO、GA和FWA算法均能較快找到理想的解;但隨著維數增加(如10維以上)局部極值點數量猛增,3種基本優化算法尋優較為困難.其中高維Rosenbrock函數被公認為難以極小化的病態二次函數,大多優化算法在尋優時極易陷入局部最優區,全局極小點的搜索極為困難.4個函數表達式的具體描述如下:

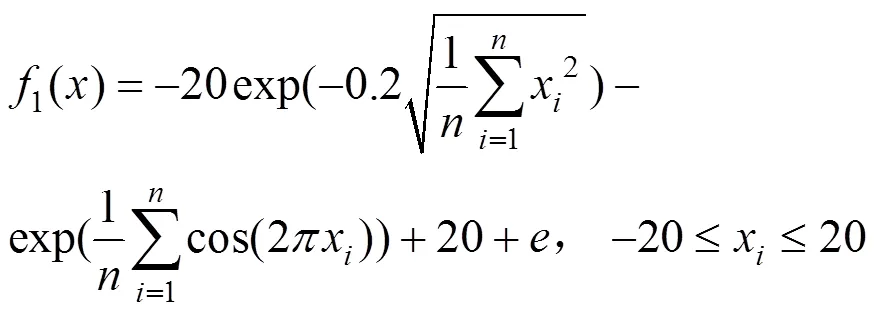
仿真分析時4個函數的尋優精度設置情況分別為10-6,10-2,10-2,10-2;PSO、GA、FWA和CFWA群體規模均為40,最大迭代次數設為2000次.其余參數設置情況為:

FWA和CFWA:爆炸半徑調節常數=240;爆炸火花數調節常數=200;爆炸火花數上限am=20;爆炸火花數下限bm=1;高斯變異火花數=50.混沌算法采用本文提出的改進正弦混沌映射SM,詳見式(8).PSO:1=2=2.0;max=0.60,min=0.06.GA:交叉概率為0.6;變異概率為0.01.

針對4個優化問題,分別采用基本PSO、基本GA、基本FWA及CFWA方法隨機進行300次獨立尋優測試,實驗結果如表1所示.

4個經典函數的測試結果表明:FWA算法的魯棒性(如尋優率)、收斂精度和收斂速度等指標較常規PSO和GA算法要更優,而本文提出的CFWA算法的整體優化性能最強;與GA算法相比,PSO算法相對簡單、收斂速度更快,但陷入局部最優的概率要更高;對于Ackley函數,4種方法均能較快找到最優解,且尋優性能良好.對于Rastrigrin函數和Griewank函數,在精度要求不高的情況下(10-2)4種方法也具有較高尋優率和收斂精度;4種方法用于10維Rosenbrock復雜函數的尋優測試對比更為明顯,在相同的預設條件下,CFWA算法表現最好,整體尋優性能明顯優于基本PSO、GA和FWA 3種算法.較好地避免了基本FWA算法的早熟收斂并提高了算法的優化效率.

表1 4種方法尋優性能對比

Table 1Comparison of optimization performances between four optimization algorithms

優化算法Ackley函數(10維)Rastrigrin函數(10維) 尋優率(%)平均精度最大迭代次數平均迭代次數尋優率(%)平均精度最大迭代次數平均迭代次數 PSO100.009.46×10-7346265.379.673.67×10-120001486.2 GA100.009.39×10-7527310.284.001.59×10-120001638.1 FWA100.003.85×10-7305234.694.337.31×10-220001217.3 CFWA100.001.03×10-7266159.3100.006.98×10-31471776.5

2 污水處理過程軟測量建模

2.1 代表樣本的獲取

神經網絡軟測量建模過程中對訓練樣本的代表性要求高.為從包含大量樣本數據的訓練樣本集中提取具有代表性的樣本數據,考慮到樣本間的相似度度量方法.

模式識別中常用樣本間的距離來衡量多元觀測數據間的相似程度.若將樣本數據和視為高維空間中的2個點,其歐氏距離為:

若將樣本數據和視為兩個向量, ||||和||||為對應的2范數,則余弦距離為:

利用變量間歐氏距離和余弦距離進行相似度分析時,由于兩種方式的描述角度不同,含義存在較大差別.歐氏距離在用于描述變量間的相似度關系時,將變量視為空間中的兩個點,強調兩樣本空間位置(即空間中兩個點之間的真實距離)的差別;余弦距離則強調兩個樣本方向(即所成夾角)上的差異.樣本間的相似度衡量時,歐氏距離雖然簡單實用,但存在將樣本不同屬性(即各指標或變量)間的差別等同看待等不足.余弦函數進行模式匹配時,當樣本間角度大于π/2或樣本間有相似的幾何方向而不同的幅度值時,其相似度度量效果不佳.

為解決這些問題,本文融合了余弦距離度量和歐式距離度量兩種方法,重新定義一項新的樣本相似度衡量指標,即:

= sec·dist (16)

式中:sec=1/Abs(cos).越大則表示樣本間的差異性越大,獨立性越強,反之亦然.

2.2 應用研究

大型污水處理裝置是一個具有非線性、不確定性、大純滯后、強耦合、分布參數、混雜系統特性的復雜工程系統[20-21].如圖1所示,某污水生化處理企業的工藝過程是典型的前置反硝化生物脫氮工藝過程.由于涉及到物理、化學和生物等多個子過程(反應),整個污水生化處理過程機理復雜多樣且物料流交互耦合[22].工藝復雜性的增加使生物脫氮工藝過程易受入水水質、水量和溫度等外界擾動的影響[23-24].如在雨天易發生流量或負荷的較大變化,發生嚴重的故障而出現超載現象;另外隨著季節溫度的變化,生物反應速率也不同.

DO是污水處理過程中的一項重要監控參數,直接關系到出水水質和控制質量,實時準確測量DO是提高污水處理效率并保障出水水質的前提[25].分析表明,影響DO的因素諸多,任一時刻該參數值均受制于各種因素的疊加作用,污水處理過程DO在線軟測量技術的研究意義重大[26].依據實際污水生化處理系統的工藝機理和經驗知識,對影響DO的多方面因素進行了深入調查與分析,研究表明生化需氧量(BOD)和固體懸浮物等6個參數對DO值都有顯著影響.軟測量建模時選取生化需氧量(BOD)、固體懸浮物、總氮質量濃度、總磷質量濃度、化學需氧量(COD)和進水流量等6個輔助變量作為模型的輸入變量, DO為模型的輸出變量.

定義向量[1,2,…,6],對應不同類型的6個輔助變量,作為軟測量模型的輸入;輸出為一維向量,對應溶解氧質量濃度.從工業現場DCS系統采集到的數據,經過異常數據剔除等預處理后得到500組樣本.為消除不同變量之間的量綱影響,采用標準差標準化(即Z-score標準化)方法對樣本數據進行標準化處理.表2為處理后的部分樣本數據.

圖1 污水處理工藝流程

表2 部分樣本數據

隨機選取400組(總數據的4/5)作為軟測量模型的建模數據,剩下的100組(總數據的1/5)作為軟測量模型的泛化數據.為簡化軟測量模型,采用上文提出的代表樣本獲取方法進行相似度分析以去除樣本集中的冗余樣本.具體樣本提取方法描述如下:樣本歸一化處理后計算兩兩樣本之間的歐氏距離、余弦距離及相應的值,得到×維上三角方陣= (δ)×l(400,1),當3,δ=0.根據預處理后數據的實際情況設置閾值,即當|δ|<0.49時剔除其中一個樣本.處理后軟測量建模樣本由400組精簡至237組.

構建基于人工神經網絡(結構為6-13-1;網絡權閾值總數為105)的污水處理過程在線軟測量模型,離線訓練算法為本文所提出的CFWA混合優化算法,并引入基本PSO、GA和FWA 3種優化算法與改進算法形成對比.軟測量建模過程中,4種優化算法的群成員規模均為50,最大迭代次數設為6000,群成員維數為105.其余實驗參數設置情況為:FWA和CFWA,爆炸半徑調節常數=240;爆炸火花數調節常數=250;爆炸火花數上限=25;爆炸火花數下限=1;高斯變異火花數=60.混沌算法采用本文提出的改進正弦混沌映射.PSO,1=2=2.0;max= 0.60,min=0.06.GA:交叉概率為0.6;變異概率為0.01.

此外,對于神經網絡訓練時初始權閾值的選擇問題,現有方法多將取值范圍設置在[-1~+1]之間.研究表明初始值的選取對于防止局部收斂和提高收斂速度均有一定程度影響.4種優化算法分別用于神經網絡權閾值的優化,優化算法的每個群成員代表一組權閾值的取值.其中,基本PSO、GA和FWA 3種優化算法的初始群成員采用常用的隨機選取方式.而在CFWA混合優化算法中,為保證初始煙花成員的質量,先采用所定義的SM混沌映射在權閾值取值范圍[-1~+1]內產生規模為5000的初始候選群體,再根據成員間的歐式距離從中提取分布均勻且群規模為50的初始煙花成員.

訓練結束保存最佳權閾值用于軟測量模型在線測量DO.表3為基于4種算法的軟測量模型訓練和檢驗結果之分析對比,ER1代表均方根誤差,ER2代表平均泛化誤差.基于CFWA算法軟測量模型的訓練和泛化效果如圖2和圖3所示.

表3 4種模型仿真結果對比

對比結果表明,與基本PSO、GA和FWA 3種軟測量模型相比,基于CFWA算法的軟測量模型具有較低訓練誤差和泛化誤差.其泛化能力明顯優于其余3種軟測量模型,精度也有較大提高,與性能測試的結果相吻合.圖3所示的溶解氧質量濃度軟測量模型泛化結果可以看出,模型的預測值(虛線所示)與實際值(實線所示)的擬合度良好,訓練過程滿足要求,泛化性能較好.

圖2 溶解氧質量濃度軟測量模型的訓練結果

圖3 溶解氧質量濃度軟測量模型的泛化結果

與基本FWA算法相比,CFWA算法較好地利用了混沌搜索機制,一方面在初始階段避免了神經網絡初始權閾值的過分隨機或盲目選取;另一方面在權閾值的優化過程中,采用了FWA和COA兩種類型搜索機制,充分發揮了各自特長并不斷進行群體和個體之間的信息交流與相互協作.表1的尋優測試結果中,CFWA算法的尋優率、尋優精度和迭代次數要優于基本FWA算法,表3的軟測量模型仿真結果中CFWA模型的訓練誤差和泛化誤差也同樣優于FWA模型,充分驗證了CFWA算法的有效性.

3 結論

3.1 提出了一種改進的混沌煙花混合優化算法并建立了基于改進算法的溶解氧質量濃度軟測量模型針對現有FWA存在的不足,設計了一種改進的兩級正弦混沌映射,利用混沌運動的遍歷性改進了FWA初始成員提取方法;此外,為進一步提高現有FWA的優化性能,將FWA算法和混沌算法有機融合,充分利用各自優勢并基于設定準則,提出了一種混沌-煙花混合優化算法.以4個經典高維復雜函數為尋優對象,對改進算法進行了尋優測試.

3.2 將改進的混沌-煙花混合優化算法應用于污水處理過程中溶解氧質量濃度的軟測量建模,并定義了一項新的樣本相似度衡量指標以提取更具代表性的軟測量建模數據.為復雜化工過程中某些無法測量或難以測量的關鍵過程變量提供了一種新的測量方法.

[1] Strokal M, Yang H, Zhang Y, et al. Increasing eutrophication in the coastal seas of China from 1970 to 2050 [J]. Marine Pollution Bulletin, 2014,85(1):123-140.

[2] Chang N N, Shiao J C, Gong G C. Diversity of demersal fish in the East China sea: implication of eutrophication and fishery [J]. Continental Shelf Research, 2012,47(47):42-54.

[3] 趙 驥,王曉霞,李夕耀,等.DO濃度對EBPR耦合SND處理低C/N污水的影響[J]. 中國環境科學, 2018,38(1):120-128.

[4] Meng F, Yang, A, Zhang G. Effects of dissolved oxygen concentration on photosynthetic bacteria wastewater treatment: Pollutants removal, cell growth and pigments production [J]. Bioresource Technology, 2017,241:993-997.

[5] 張質明,王曉燕,潘潤澤.一種改進的不確定性水質模型參數率定方法[J].中國環境科學, 2017,37(3):956-962.

[6] Qiu Y, Liu Y, Huang D. Data-driven soft-sensor design for biological wastewater treatment using deep neural networks and genetic algorithms [J]. Journal of Chemical Engineering of Japan, 2016,49(10): 925-936.

[7] 胡 康,萬金泉,馬邕文,等.基于模糊神經網絡的A2/O工藝出水氨氮在線預測模型[J]. 中國環境科學, 2012,32(2):260-267.

[8] Canete J F, Saz-Orozco P, Baratti R, et al. A soft-sensing estimation of plant effluent concentrations in a biological wastewater treatment plant using an optimal neural network [J]. Expert Systems with Applications, 2016,63:8-19.

[9] 史 斌,姜繼平,王 鵬.基于高頻在線水質數據異常的突發污染預警[J]. 中國環境科學, 2017,37(11):4394-4400.

[10] Tan Y, Zhu Y C. Fireworks algorithm for optimization [C] //Proceedings of 1st International Conference on Swarm Intelligence. Berlin, Germany: Springer, 2010:355-364.

[11] Li J, Zheng S U, Tan Y. Adaptive fireworks algorithm [C]// Proceedings of 2014 IEEE Congress on Evolutionary Computation. Piscataway, NJ, USA: IEEE, 2014:3214-3221.

[12] Rajaram R, Palanisamy K, Ramasamy S, et a1. Selective harmonic elimination in PWM inverter using firefly and fireworks algorithm [J]. International Journal of Innovative Research in Advanced Engineering, 2014,1(8):55-62.

[13] 吳 瓊,曾慶鵬.基于多目標煙花算法的關聯規則挖掘[J]. 模式識別與人工智能, 2017,30(4):365-376.

[14] Pavao L V, Costa C B B, RavagnaniM. Large-scale heat exchanger networks synthesis using simulated annealing and the novel rocket fireworks optimization [J]. AICHE Journal, 2017,63(5):1582-1601.

[15] Zheng S Q, Li J Z, JanecekA. A cooperative framework for fireworks algorithm [J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2017,14(1):27-41.

[16] Ma T N, Niu D X. Icing forecasting of high voltage transmission line using weighted least square support vector machine with fireworks algorithm for feature selection [J]. Applied Sciences, 2016,6(12): 438-456.

[17] 張以文,吳金濤,趙 姝,等.基于改進煙花算法的Web服務組合優化[J]. 計算機集成制造系統, 2016,22(3):422-432.

[18] 陳如清,俞金壽.混沌粒子群混合優化算法的研究與應用[J]. 系統仿真學報, 2008,20(3):685-688.

[19] 尤 勇,王孫安,盛萬興.新型混沌優化方法的研究及應用[J]. 西安交通大學學報, 2003,37(1):69-72.

[20] Li X, Feng Y, Chen H. Electric biological coupling process (EBCP) for wastewater treatment: a general review [J]. Desalination and Water Treatment, 2017,94:11-24.

[21] 宋 留,楊 沖,張 輝,等.造紙廢水處理過程的高斯過程回歸軟測量建模[J]. 中國環境科學, 2018,38(7):2564-2571.

[22] 王衫允,馬 斌,賈方旭,等. AAO污水處理工藝中厭氧氨氧化效能及微生物交互作用[J]. 中國環境科學, 2016,36(7):1988-1996.

[23] 趙 超,戴坤成,王貴評,等.基于AWLS-SVM的污水處理過程軟測量建模[J]. 儀器儀表學報, 2015,36(8):1792-1800.

[24] 張 姚,韓海成,王偉剛,等.溶解氧對CANON顆粒污泥自養脫氮性能的影響[J]. 中國環境科學, 2017,37(12):4501-4510.

[25] 喬俊飛,付文韜,韓紅桂.基于SOTSFNN的溶解氧濃度控制方法[J]. 化工學報, 2016,67(3):960-966.

[26] 張 偉,喬俊飛,李凡軍.溶解氧濃度的直接自適應動態神經網絡控制方法[J]. 控制理論與應用, 2015,32(1):115-121.

Prediction of dissolved oxygen concentration in wastewater treatment process based on improved FWA-NN.

CHEN Ru-qing1*, YU Jin-shou2

(1.College of Mechanical and Electrical Engineering, Jiaxing University, Jiaxing 314001, China；2.Research Institute of Automation, East China University of Science and Technology, Shanghai 200237, China)., 2018,38(10)：3739~3746

To realize the quick and accurate measurement of the dissolved oxygen concentration (DO) in wastewater treatment process, a novel chaos-fireworks algorithm (FWA) based hybrid optimization algorithm was proposed and a neural network on-line soft-sensor model was built based on the improved algorithm. According to the property of the data collected from wastewater treatment process, a new measure of similarity degrees between samples was defined to extract more responsive modeling data. In the novel algorithm, a modified two-level sinusoidal chaotic mapping was defined and the initial members of FWA were well selected by utilizing the ergodicity of chaos. As a result, the quality of the initial population in standard FWA was improved. Next, the search mechanism of FWA was modified by introducing chaos optimization algorithm. The optimization procedure was divided into two phases and the population was divided into two subpopulations according to the predefined criterion. Test results confirmed that the improved FWA had higher convergence speed and convergence accuracy. The novel soft-sensor modeling method and the sample data extraction method was used to build a soft sensor model for real-time measuring DO in wastewater treatment process.Application results indicated the root mean square error and the root mean square error of this model were 0.0175 and 0.0118 respectively, it had good generalization ability.

wastewater treatment process；dissolved oxygen concentration；soft sensor modeling；fireworks algorithm；similarity measure

X703

A

1000-6923(2018)10-3739-08

陳如清(1979-),男,江西萍鄉人,副教授,博士,主要研究方向為復雜工業過程建模與故障診斷.發表論文40余篇.

2018-03-21

浙江省基礎公益研究計劃項目(LGG18F030011);國家自然科學基金資助項目(61603154)

* 責任作者, 副教授, 10555322@qq.com