信息物理系統可調度性分析的執行時間優化方法
張 晶,陳 垚,孫 俊,范洪博
(昆明理工大學 信息工程與自動化學院,昆明 650500)
1 概 述
信息物理系統(Cyber-Physical System,CPS)通過軟件的計算進程控制外部環境的物理進程,并由一系列傳感器組件與網絡節點完成搜集環境信息、系統間通信、反饋控制等任務.為了獲取精確的環境信息并做出實時反應,根據具體的不同任務,系統需要自動調整計算邏輯與資源配置,采用針對性的調度策略,實現計算世界與物理世界的高效融合[1].CPS系統的連續物理系統與離散計算系統相互作用、互相影響[2],其中計算進程由包含獨立控制線程、可異步傳遞消息與交流的執行器(Actor)通過輸入、輸出含有特定信息的事件信號實時控制物理實體.然而物理環境的時間變量為連續信號,而計算系統為離散信號.計算進程若要控制物理進程,需要將物理連續變量由微分不變式計算得到一個收斂于離散變量中對應的不動點收斂函數,求解該不動點即可使系統內外環境在時間度量與表示上保持一致[3].
由于設計的不同需求,CPS系統的開發必須考慮系統時間信號、事件價值、執行周期、資源消耗等約束條件,使開發過程可以得到一個詳實的性能評估與描述.對于CPS在復雜環境下的任務執行要求,系統能否完成調度任務就顯得異常重要,這就要求對其可調度性進行驗證,而CPS物理進程與計算進程實時交互過程中,對其任務集的可調度性進行直接驗證非常困難,為此需要在保證系統正確性的前提下,能準確分析可調度性的方法[4].此前,時間自動機被廣泛用于測試實時系統的調度性.其中Elena F等人[5]提出了一種稱為任務自動機的實時系統模型,其異步流程定位于自動機狀態位置,從而表達出任務到達與依賴模式.桂盛霖等人[6]實現了一種支持分布式系統任務實時調度分析工具SCT,其分析結果精確但分析時間偏長.M Stigge等人[7]基于有向圖模型提出一種pseudo-polynomial調度算法,對不同模型的工作類型、執行條件與循環結構的表達方式進行優化.然而這些方法并沒有提及計算世界與物理世界深度交互時,系統的調度性如何轉換為自動機的可達性進行判定.
本文考慮在上述技術研究的基礎上,定義多元的CPS系統任務調度約束,以超致密時間模型(Superdense Time Model,SDT)計算離散變量不動點并表達系統全局時間信號.提出一種基于有限狀態機(Finite State Machine,FSM)的執行器狀態自動機(Actor State Automata,ASA)分析方法對CPS調度性進行分析,并基于此方法,提出一種基于決策樹的ASA狀態集分類搜尋策略(A classified search strategy of state set for ASA based on decision tree,DT-ASA*).最后通過PtolemyII平臺[8,9]建立模型,分析系統模型的精確性與性能.
2 系統模型
CPS系統由物理設備與計算系統組合而成,通過傳感器、制動器與網絡節點相互作用.如圖1所示,計算系統在PtolemyII平臺仿真時被定義為一種基于面向執行器(Actor-oriented)的并發性模型與通信交流策略構成的并發計算模型(Model of Computation,MoC)[10],利用事件驅動結構,通過異步回調操作(asynchronous callbacks) 函數可將所有事件信號按事件時間戳順序處理.
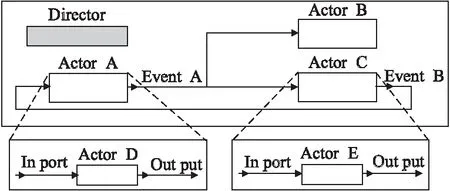
圖1 基于面向執行器模型的基本等級架構Fig.1 Basic level architecture based on actor-oriented model
2.1 CPS系統執行約束條件
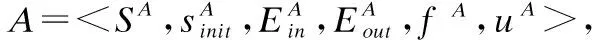
·SA是執行器A狀態集合,且SA≠?;
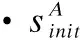
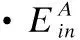
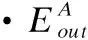

基于面向執行器的并發計算模型,是一種具有層次感的程序組件組成的系統模型,不同層次的模型或同一層次的組件通過執行器進行通信,其方式即通過輸入、輸出端口接收或送出執行事件.
定義2.(事件)事件信號標簽為一個五元組E=
·C代表事件所處信道集合,其單值子集c代表某個輸入行為或輸出行為,并且{e1,e2|e1∈Ein∨e2∈Eout},則f(sinit,e1,cin)=u(sinit,e1)×e2,其中e2∈cout;
·Φe是事件e∈E的約束條件集合;
·T是執行器處理事件的系統全局時間;
·SE是事件E的狀態集合,se∈SE是事件e的時間戳確定的事件狀態.
由于不同的設計需求,CPS的事件考慮多種約束條件,如Φe=δe×Re×Ve.
δe為事件時間戳所確定的時序約束,時序約束內部元素是時鐘集合X?T到非負實數+的映射,并且是系統預計執行器處理事件e的時間,即:;t是系統當前運行時間,y為影響參數[11].
Re為執行事件e所消耗的資源,該約束由事件等待時產生的能耗,執行任務的消耗,及是否正常執行等因素決定.令de為事件e截至時間,re為事件就緒準備被執行的時間,εe為完成處理fA任務的時間,對于當前時間t∈T,事件e處于等待時間或執行時間有如下狀態:
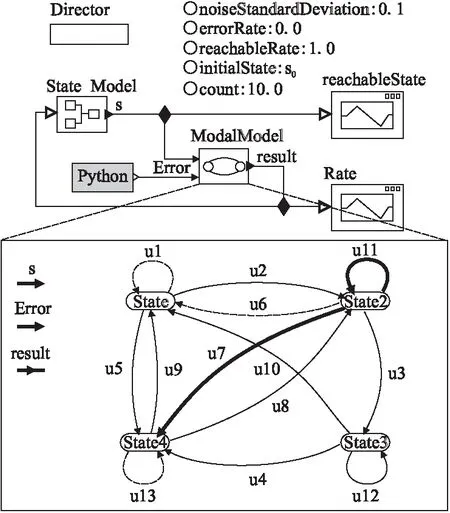
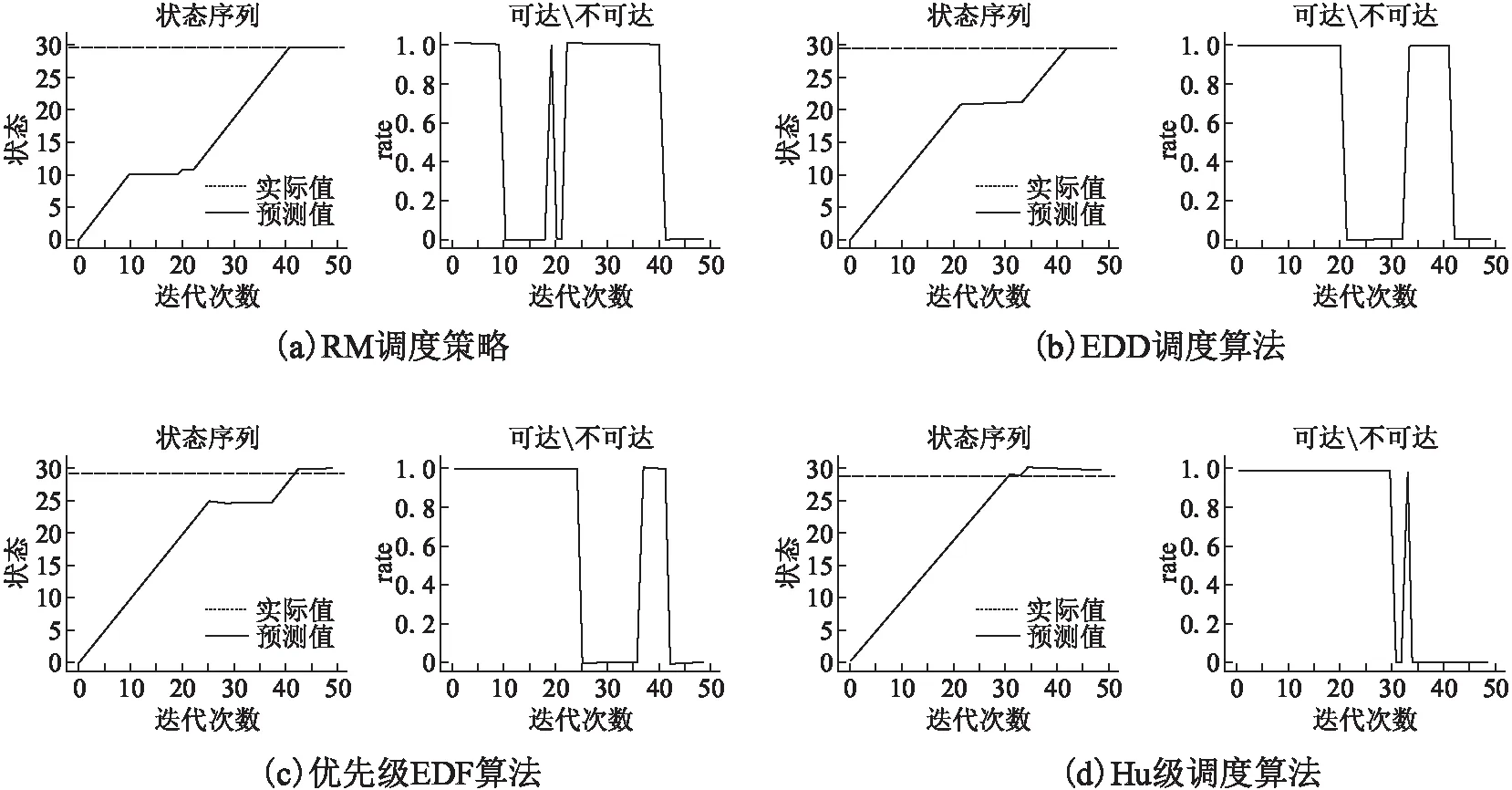
(a)runninge=(re (b)readye=((t=re∧t (c)suspende=(t≤re∨(t (d)sleepe=(t Ve為事件價值量約束,由事件e產生的數據質量Qe與對應的執行器A的信息冗余度χA決定,H(A)為執行器A輸出事件時的信息熵[12],滿足: CPS中計算進程為離散的,物理進程為連續的,若T為任意小常數的倍數,則無法表達其語義,故不能以時鐘計數表達執行器輸出事件的時間戳排序.考慮集合×代替+作為時鐘集合X?T的映射,表示執行器處理事件的系統全局時間T,此時時間值為數組(?,n)∈T,其中?為時間長度,n為離散時間瞬間的某一序列值[13]. 定義3.超致密時間(SDT)表示為(?,n)∈(T=×),?∈表示離散步長,n∈表示離散步數.若(?,n)≥ (?′,n′),則有?≥?′∨(?=?′∧n≥n′).對于SDT有如下性質[14]: ·對于(?,n)在集合T上有如下的下降集: ·T的下降集由T本身表示; 定理1.在超致密時間中,若Y為實時規則集合,Y′為非實時規則集合,對于?e∈E,當且僅當?t∈(?,n),有(e,t)∈Y,則e∈Y′. 證明:1)根據定義3,(?,n)∈T,則T的下降集為Ζ[?,n]或Ζ(?,n),其中,若?∈,則T的下降集為Ζ(?,∞).故若?t∈(?,n),使得(e,t)∈Y,說明e的執行序列為排序的. 2)若t為任意實數值的時間序列,則?(e,t)∈Y,若?q∈,使X內部元素x為q的整數倍,則?n∈,0≤i′≤i,使xi=xi′+nq.由t∈(?,n),得ti=ni?.由于存在延遲,故總有q′≤q,使?i-?i′=nq′≤nq,由證明1)可知(ti-ti′)與?i-?i′滿足相同約束Φe,故構造(e,(?,n))作用于執行器,其事件輸出路徑滿足與輸出Cr=f×u相同的運行路徑.故當(e,t)∈Y,有e∈Y′. 得證. 對于集合H(A,E),有如下屬性: ·e∈E為執行器A在time(?,n)控制下的輸出事件: (a)?e=ep為周期事件(periodic events),其輸出事件時間間隔p1為固定常數; (b)?e=ea為非周期事件(aperiodic events),其輸出事件時間間隔p2是以需求確定的最小下界; ·若?se∈SA,E=sleepe∨suspende,則執行器A的執行周期p→∞; ·執行器A中任意事件e順序執行的必要條件為?t=(e,(?,n))≥p(me,(?,n))|m=1,2,,…,n-1},即每個事件由狀態readye→runninge需要前n-1個事件執行完成才能開始; ·執行器A中任意事件e必須滿足Φe=δe×Re×Ve. 圖2 執行器內部狀態轉移任務示例圖Fig.2 Sample figure of state transition tasks in an actor 系統狀態被定義為在某個特定的時刻,系統對應的條件狀況.狀態變量表示為s∈Σ,Σ為系統所有可能狀態的集合,有限狀態機(FSM)是一種Σ為有限集合的狀態機,在FSM中,系統行為被表達為狀態集合,并在其中通過某種規則管理各個狀態間的轉移. 定義4.(有限狀態機)有限狀態機為六元組<Σ,CI,CO,s0,Δ,F>,其中: ·Σ為狀態機內所有可能狀態的集合; ·CI為函數:CI=Cin→Ein∪{absent},{absent}表示信道Cin可用; ·CO為函數:CO=Cout→Eout∪{absent}; ·s0為初始狀態,s0∈Σ; ·Δ為變量值; ·F為函數:F=Σ×CI×Δ→Σ×CO×Δ. 對于一個確定的有限狀態機,若任意狀態,最多有一個輸入值可以激活一個轉移,則稱其具有確定性;若任意狀態,每個輸入值都至少能激活一個轉移,則稱其為可接受的.狀態間的轉移為有限狀態空間離散動態與輸入到輸出的映射. FSM可并列異步組合,對于a、b狀態機組合成的c狀態機,其執行過程中有如下語義: 1)c的響應為a或b其中的一個的響應,并且選擇是不確定的; 2)c的響應可能為a或b其中的一個的響應,也可能為a、b的共同響應,并且選擇是不確定的,執行結果可能導致沒有響應; 3)c的響應如何決定,由外部環境選擇. 如圖3為一組并列異步組合FSM,通過不同約束條件(guard)選擇轉移狀態.其中,狀態b可分層為狀態c與狀態d,當處于狀態b時表示處于狀態c或狀態d.框圖3-Ⅱ為框圖3-Ⅰ的等效表示. 圖3 并列異步組合FSM示例圖Fig.3 Sample figure of side-by-side composition FSM 本節定義一種帶約束條件有限狀態機的特定子類,命名為執行器狀態自動機,與以往技術原理相同,本文采用基于自動機理論,將系統可調度性問題轉換為可達性問題進行分析.帶約束條件有限狀態機為<Σ,E,L,L0,X,Φ,Δ,f>,與上述符合含義相同的,Σ為狀態機內所有可能狀態的集合,E是有限事件集合,L為位置的有限集合L0為初始位置集合,并有L0?L,X?T為時鐘集合,Φ為E的約束條件集合,Δ為變量值,f為狀態轉移函數. 定義5.(執行器狀態自動機)執行器狀態自動機為十二元組<Σ,E,L,L0,ρ,σ,X,δ,R,V,Δ,f>,其中: ·Σ為狀態機內所有可能狀態的集合,存在Σre表示可執行狀態集,Σerr表示不可執行狀態集,并且Σre,Σerr∈Σ; ·E為有限事件集合,存在E=En∪Ew,En為內部事件集合,Ew為外部事件集合,其行為與定義3第1子句(c)相符; ·L為位置的有限集合,存在L=Lbasic∪Lcom,其中Lbasic為基礎位置集合,Lcom為異步組合位置集合; ·L0?Lbasic為初始位置集合; ·l0,l1∈Lcom,e∈E,s∈Σ,l1=l0(s×e)→ρ(l0),?l∈Lcom,ρ(l)表示l的子位置,而ρ-1(l)表示l的父位置; ·σ={&&,‖,?}表示每個位置間的關系,若父子位置為&&關系,則?l1=ρ(l0)=Sact,其中Sact表示活躍狀態,若父子位置為‖關系,則只存在一個l1=ρ(l0)=Sact,&&關系與‖關系組合成的位置集合為Lcom,對于L0?Lbasic=?說明其沒有父子關系的位置; ·時鐘集合X?time(?,n)為時鐘集合,滿足超致密時間表達:(?,n)∈(T=×); ·δ×R×V為約束條件,其定義與2.1節對δe、Re及Ve的描述相符; ·Δ為變量值,每個變量的值域都為有限的; ·f=Σ×E×L×2X×Φ(δ)×Φ(R)×Φ(V)×Δ表示狀態轉移關系. 由定義5第6子句可知,若位置l=Sact且σ(l)=||,則?!l′∈ρ(l)使得l′=Sact;若位置l=Sact且σ(l)=&&,則?!l′∈ρ(l)使得l′=Sact. 定理2.帶約束條件有限狀態機是可判定的,則執行器狀態自動機一定也是可判定的. 證明:設K=<Σ,E,L,L0,X,Φ,Δ,f>為帶約束條件有限狀態機,按如下條件可編碼為對應的特定子類K′=<Σ′,E′,L′,L0′,ρ,σ,X′,δ,R,V,Δ′,f′>: 1)K中活躍狀態位置集合{L|Sact}中任意位置l∈L都對應K′中某一位置l′∈L′.若l的初始位置為L0?Lbasic?K,則l′的初始位置為L0′?Lbasic′?K′,其中E′=E; 2)K中的時鐘集X對應K′中的時鐘集X′,且滿足X=X′,f′(δ)=f; 3)若{L|Satc,?l∈L}對應K′中的位置l′∈L′,則狀態轉移關系為f′(l′)=∧{L|Satc,l∈L}f(l); 4)若在K中有從li到lj的狀態轉移f(si×cin×ei),與一組從Lm到Ln的狀態轉移行為集合H(A,E)?F,且狀態為li∈{Li|Sact},Lm∈{Li|Sact},lj∈{Lj|Sact},ln∈{Lj|Sact},其中{Li|Sact},{Lj|Sact}?{L|Sact},li,lj∈Lbasic,Lm,Ln?L.那么在K′中同時對應狀態轉移f′(si′×cin′×ei′)={L|Satc},u(si′×cin′×ei′)={Lj|Satc},u∈F,且f′(δ×R×V)=∧E?H(A,E)f(Φ). 通過編碼后,K中?s∈∑=({L|Sact},X)對應K′中某一狀態s′∈∑′=(l′,X′),并且l′={L|Sact}.若K中?si∈∑=({Li|Sact},Xi)可由s到達,則si在K′中對應的si′也可由s′到達.由定義6與定義7可知,執行器狀態自動機的可達性是可判定的. 得證. 對于ASA的模型檢測,需要計算ASA的可到達狀態集合,檢測ASA是否滿足超致密時間邏輯描述的系統規格,并使用調度策略進行驗證.考慮一種基于決策樹的ASA狀態集分類搜尋策略(A classified search strategy of state set for ASA based on decision tree,DT-ASA*),并且在PtolemyII平臺上基于此策略建模,用于分析ASA方法的精確度、執行時間及內存使用率. DT-ASA*策略實質是個遞歸的過程,若在下列情況發生時產生遞歸返回: 1)屬性集中的樣本全屬于同一類別,即全可達或不可達,則無需分類; 2)屬性集為空,或樣本屬性取值完全相同,則無法分類:此情況下將此結點作為葉結點,其類別為樣本中最多的類別; 3)結點內樣本集為空,無法分類:此情況下將其父結點作為葉結點,其類別為樣本中最多的類別. 作為每個結點劃分的關鍵,參考著名的C4.5決策樹算法,使用增益率(gain ratio)選擇最優劃分屬性,由狀態集s= 算法1.DT-ASA*策略 輸入: 訓練集K={s0,s1,…,sm} 屬性集Γ={reachable,error} 1.初始化: s0={e0,I0,x0,δ0,R0,V0} 2. Re:={s0},Error=[] 3.DT-ASA*(K,Γ): 4. 生成結點node 5.while∑≠? 6.ifK中的樣本屬于同一類別reachableORerror 7. 將nodfe標記為reachableORerror 8.return 9.endifΓ=? 10.if或K中的樣本在Γ取值相同,then 11. 將node標記為葉結點,其類別標記為K中樣本最多類 12.return 13.endif 17. 選擇gain_ratio(K,s)較大的屬性作為最優劃分屬性Γ* 18.forΓ*的每個取值a* 19.為node生成一個分支 20.令Ka表示K在Γ*上取值為a*的樣本子集 21.ifKa為空,then 22.將分支節點標記為葉結點,其類別標記為K中樣本最多的類 23.return 24.else 25.以DT-ASA*(K,Γ、{Γ*})為分支結點 26.end 27.if存在s′屬于reachableands′不屬于Re 28. Re:=Re∪{s′} 29.else 30. Error.extend(s′) 31.end DT-ASA*策略的輸入為系統狀態及屬性集合,輸出為系統狀態分類后的狀態屬性分類集合. 測試DT-ASA*策略:本測試使用處理器為1.6GHz雙核Intel Core i5,RAM為8.00GB的MacBook Air PC機,其系統為macOS Sierra,以系統自帶的Python 2.7編程運行,使用加州大學伯克利分校[15]的數據集作為訓練集. 由于數據需要作為4.2節所建立模型的變量輸入,故測試的決策樹結果為字典模式保存,其中可達狀態集存入字典Re,不可達狀態集存入列表Error: >>> DT-ASA*Tree {′states′:{‘disabled’:′error′,′act′:{′timing sequence′:{‘overrun’:′error′,′x:=0′:{′quantity of value′:{′satisfy′:{′clock constraint′:{′satisfy′:{′energy consumption′:{′equality′:{′events′:{′ready′:′reachable′,′running′:′reachable′,′suspend′:′reachable′,′sleep′:′error′}},′low′:{′events′:{′ready′:′reachable′,′running′:′reachable′,′suspend′:′reachable′,′sleep′:′error′}},′higher′:′error′}},′dissatisfy′:′error′,′equality′:{′energy consumption′:{′equality′:{′events′:{′ready′:′reachable′,′running′:′reachable′,′suspend′:′reachable′,′sleep′:′error′}},′low′:′events′:{′ready′:′reachable′,′running′:′reachable′,′suspend′:′reachable′,′sleep′:′error′}},′higher′:′error′}}}},′dissatisfy′:′error′}}}}}} 其中′reachable′表示可達狀態,′error′表示不可達狀態,事件約束條件有runninge、readye、suspende以及sleepe,時序約束若不是‘overrun’則在狀態轉移時重置時鐘′x:=0′,約束條件集合Φe為′clock constraint′,′energy consumption′和′quantity of value′.測試結果符合數據集運行結果. UC Berkeley的PtolemyII平臺由Edward Ashford Lee教授團隊研發,用于驗證包含時間和行為類型屬性的組件交互過程,并支持分層設計實時嵌入式異構系統[8].本節建立的DT-ASA*策略模型,使用4.1節所述MacBook Air PC開發環境,平臺版本使用PtolemyⅡ10.0.1Mac OS X版. 建立的模型如圖4所示,Director為系統調度器,使用2.2節所述的SDT時間控制系統全局時間.Director調度器右側為Δ變量值,引號左邊為變量名,引號右邊為變量初始值.State Model為狀態產生模塊,內部隨機產生初始狀態s0,由不同的調度策略產生狀態序列并輸入Modal Model模塊分析檢測,生成result實時反饋回State Model,使其更新更優的狀態序列.Modal Model內部結構為執行器狀態自動機模型,其左端輸入不可達狀態集列表Error.模型輸出結果表現在曲線生成器reachableState與Rate中. 圖4 DT-ASA*策略模型Fig.4 Model of DT-ASA* strategy Modal Model中黑色箭頭s與Error表示輸入參數,result表示輸出參數.虛線狀態轉移邊為默認轉移(default transition),其優先級僅低于普通轉移.加粗的邊表示經歷轉移(history transition),為復位轉移的一種形式,目標狀態會停留于它最后所處的狀態或最初狀態.RelationParameter為轉移關系,圖中以u表示,具體如下: u1:(output:s = reachableRate); u2:(guard:error,output:s = 0,set:count = 0); u3:(guard:count < 10 && s0<= ScheOn,output:s = reachableRate,set:count = count + 1); u4:(guard:count < 10&& s0> ScheOn,output:s = errorRate,set:count = count + 1); u5:(guard:!error &&s0>= ScheOff,output:s =errorRate); u6:(output:s = 0); u7:(guard:count < 10,output:s = errorRate,set:count + 1); u8:(guard:error,output:s = 0,set:count = 0); u9:(guard:!error &&s0<= ScheOff,output:s = reachableRate); u10:(output:s = 0); u11:(guard:count < 10,output:s = reachableRate,set:count + 1); u12:(output:s = errorRate); u13:(output:s = errorRate); 測試所涉及的調度策略包括單調速率(RM)調度策略、最早交貨期(EDD)調度算法、優先級最早時限優先(EDF*)算法、Hu級調度(Hu level scheduling)算法.其中RM策略為一種簡單的搶占式調度策略,為周期較小的任務分配較高的優先級;EDD算法也稱為Jackson算法,它只根據時限順序執行,與任務間相對順序無關,時限最早的優先級最高;EDF*算法為簡單的EDF改進方法,是一種支持任務到達并且將最大延遲最小化的簡單優先級最優算法;Hu級調度算法為多處理器調度最簡單的方法,作為關鍵路徑(critical path)算法的一種,根據最長完成時間制定優先級圖的路徑. 模型中不同調度策略的狀態轉移都處于執行狀態或就緒狀態間相互轉換.首先不使用Modal Model產生的result進行反饋,而由不同的調度策略直接將狀態序列輸入reachableState得到實際值,然后使用4.2節描述的系統模型,將結果輸入reachableState與Rate得到預測值,通過對比得到DT-ASA*策略模型的精確性.分析結果如圖5(a)-圖5(d)所示.對比獲得實際狀態序列與預測狀態序列的執行時間以及內存使用率,結果如表1所示. 圖5 DT-ASA*策略模型的精確性分析Fig.5 Analysis of accurateness for DT-ASA* strategy Model 由圖5所示,使用調度策略實際產生30次狀態轉移,在圖5(a)與圖5(b)中,DT-ASA*策略模型能很好地預測出最終狀態轉移次數,其中可達不可達圖為DT-ASA*策略得出的二分類結論,即在迭代過程中,若當前位置為可達狀態輸出1.0,若為不可達狀態則輸出0.0.狀態序列圖與可達不可達圖互相對應,明顯看出,位置狀態為1.0時,狀態轉移過程中增加狀態序列,位置狀態為0.0時,狀態轉移停滯,直到搜索到下一可達狀態.圖5(c)、圖5(d)與圖5(a)、圖5(b)相似,預測值與實際值基本一致,但可以看出在狀態序列穩定后,圖5(c)、圖5(d)的預測值要比實際值略高,即仍然存在過度匹配的現象. 表1 DT-ASA*策略模型的性能分析Table 1 Analysis of performance for DT-ASA* strategy Model 分析不同測試算法在系統模型中的性能,將算法在模型中得到實際值的執行與得到預測值的執行分別運行20次,得到平均執行時間與平均內存使用率.由表1所示,可以看出4種不同的調度策略在模型中的執行情況,其中迭代次數為圖5中橫坐標的迭代次數.當使用DT-ASA*策略模型時,對于RM調度策略,執行時間提高33.33%,同時多消耗45.16%內存資源;對于EDD調度算法,執行時間提高45.32%,同時多消耗23.53%內存資源;對于優先級EDF算法,執行時間提高37.01%,同時多消耗45.95%內存資源;對于Hu級調度算法,執行時間提高33.80,同時多消耗32.56%內存資源. 表2 關鍵符號列表Table 2 Key compliance list 由仿真結果可以得出結論,DT-ASA*策略模型所得到的預測值與實際值基本一致,但仍然存在過度匹配的現象,需要進一步改進,雖然使用模型預測任務狀態能極大減少執行時間,但同時也會消耗更多內存資源. 本文針對CPS系統可調度性分析問題.首先定義了CPS系統執行約束條件,然后以SDT表達系統全局時間,在定義了帶約束條件的執行器行為后,提出了一種基于有限狀態機的執行器狀態自動機分析方法,并對執行器狀態自動機判定性問題進行證明.最后提出一種基于決策樹的執行器狀態自動機狀態集分類搜尋策略,通過可包含時間和行為類型屬性組件交互過程進行驗證的PtolemyII平臺建立策略模型.通過仿真得出結論,該策略得到的預測值基本符合實際值,并且明顯降低執行時間,但策略仍然存在不足,例如會消耗更多內存資源以及存在過度匹配的現象,需要在今后的工作中加以改進.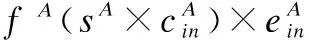
2.2 全局時間信號的表達
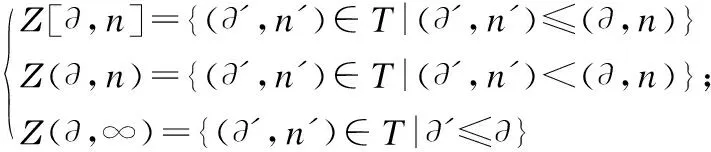
2.3 帶約束條件的執行器行為
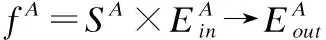

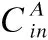
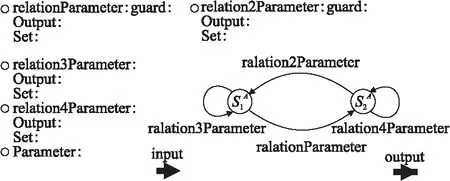
3 執行器狀態自動機

3.1 有限狀態機語義
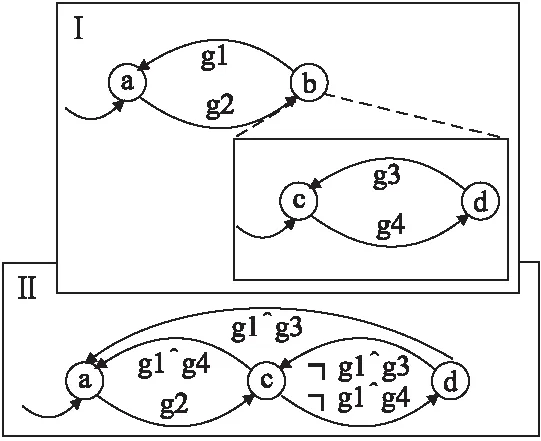
3.2 執行器狀態自動機語義
3.3 執行器狀態自動機判定性證明
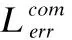
3.4 DT-ASA*策略
4 性能驗證
4.1 建立DT-ASA*策略模型
4.2 仿真結果


5 總 結

