機會網絡中基于社團的能量均衡路由算法

姚明輝,張 勝,王 瑜,黃 毅

(南昌航空大學 信息工程學院,南昌 330063)

1 引 言

機會網絡是由延遲容忍網絡(DTN)和移動自組網絡(MANET)發展而來的新型網絡.它是一種源節點和目標節點之間不存在完整鏈路,利用節點移動帶來的相遇機會實現通信的延遲容忍自組網絡[1].該類網絡具有節點部署稀疏、節點通信距離短、存儲容量有限和拓撲結構多變等特點.隨著延遲容忍網絡和移動自組網絡研究和應用的不斷深入,機會網絡越來越受到人們的關注,逐漸成為研究熱點.該網絡廣泛應用[2,3]于野生動物監測、手持設備組網、車載網絡、環境監測和交通管理等領域.應用前景十分廣闊.

機會網絡節點之間是利用節點移動帶來的相遇機會進行通信.因此,節點之間的通信鏈路具有間斷性,傳統的基于完整鏈路通信的路由算法已不再適用機會網絡.取而代之的是＂存儲-攜帶-轉發＂的消息轉發模式.這種新的消息轉發模式的核心挑戰是:(1)消息轉發時機與消息轉發節點如何選取;(2)源節點和目標節點之間的最優通信鏈路如何確定;(3)不同網絡模型對轉發機制的影響.

為了提出能夠適用于機會網絡的消息傳輸機制,國內外研究人員提出了許多路由機制,主要有:基于轉發的路由策略(如:Direct Delivery[4]等);基于復制的路由策略(如:PRoPHET[5]等).這些算法多采用多副本機制,雖然可以提高消息傳輸成功率和降低傳輸延遲.但,數據復制會給帶寬有限的機會網絡帶來很大的網絡開銷,也給存儲空間有限的節點帶來很大的存儲開銷.多副本路由策略不適合于資源受限的機會網絡．在節點能量和帶寬受限的情況下,單副本路由機制在網絡資源開銷方面有較強的優勢.

在許多應用中,機會網絡節點一般由人類(或動物)攜帶,而人的移動具有社會屬性.通過分析人類行為可以發現,人類行為具有時空受限特性.因此,機會網絡節點移動也具有時空受限特性,即節點的移動受到時間和空間的限制,表現出周期特性.有效的利用機會網絡的時空特性,能提高節點間的消息傳輸效率.雖然研究者已經提出了許多基于節點社會特性的路由策略,但是針對節點的時空受限特性還有待進一步的研究,在路由策略方面需進一步提高消息傳輸效率和均衡網絡能量.針對節點移動的時空特性,本文設計了一種時空受限的移動模型,并在此基礎上提出一種路由算法.本文的主要貢獻如下:

①設計了節點移動模型RTSM,該模型體現了節點的時空受限特性和周期特性,反應了機會網絡節點的移動規律,符合實際場景需求.

②通過綜合考慮節點的相遇概率、相遇周期和剩余能量,設計了基于社團的能量均衡路由算法.該算法利用節點移動的時空特性,保證了消息高效傳輸、均衡了節點能量、延長了網絡生存期.

2 相關工作

2.1 移動模型

機會網絡移動模型是以刻畫節點相遇特征為核心.移動模型決定了節點的相遇概率與相遇時間分布.而機會網絡就是利用節點的相遇來實現消息的傳輸.因此,與傳統的延遲容忍網和移動自組網相比,機會網絡移動模型的研究更為重要.

目前,在機會網絡移動模型研究方面取得了很多研究成果.文獻[6,7]綜述了機會網絡移動模型研究現狀.從移動模型研究角度可以將移動模型分為兩類:一類是基于理論的移動模型,另一類是基于真實場景的移動模型.前者主要從理論方面構建分析移動模型,如,隨機移動模型、高斯-馬爾科夫移動模型等.后者主要通過分析節點的真實移動軌跡構建移動模型.如:基于社區的移動模型、基于地圖的移動模型、基于工作日的移動模型、基于事件的移動模型等.

本文主要研究的是基于真實場景的移動模型.分析節點的真實移動軌跡可以發現,節點的移動具有時間和空間受限特性.即節點會按照一定的時間到同一個地點聚集,如,學生需要按照課表在指定的時間到指定的教室上課;員工會按照公司規定時間到辦公室上班等.針對節點這種社會特性文獻[8]提出了用戶移動模型.該模型將節點的空間分為家社區和其他社區,節點以更大的概率留在家社區.該模型很好的反應的節點的空間特性,但沒有考慮節點的時間特性;文獻[9]提出了時變的用戶移動模型,該模型很好的反應了節點的時間特性,但并沒有體現節點的空間受限特性.文獻[10,11]也提出了具有類似特性的節點移動模型,但都沒有同時考慮節點的時間和空間受限特性.

本文根據節點的時空受限特性設計了移動模型.節點的移動受到時間和空間的限制,同時具有周期特性.該模型體現了節點移動的時空受限社會特性,符合一定場景的需求.

2.2 路由算法

目前,越來越多的研究者關注機會網絡路由算法,國內外研究者從不同的角度提出了許多機會網絡路由算法.最早的算法大多從消息復制方面增強機會網絡的消息傳輸.Epidemic算法和Spray and Wait是基于洪泛的思想增加網絡中消息副本數量來提高路由效率;PRoPHET,MaxProp算法通過相遇概率決定消息是否轉發.

此外,具有社會特性的復雜路由算法也被相繼提出.文獻[12]提出一種基于社區機會網絡的消息傳輸算法.該算法根據節點之間的相遇頻繁程度,將節點劃分為不同的社區,自適應的控制消息拷貝數量并依靠活躍節點傳輸消息.文獻[13]提出了一種預測輔助的動態多副本數據傳輸機制.該方法根據節點時空維度相遇特征預測節點接觸概率,引入區間數不確定理論描述節點接觸的不確定性.文獻[14]根據節點周期性的運動規律,將時間離散化并給定了時間片上節點的接觸概率,提出了一種機會路由算法.文獻[15]根據節點周期性相遇規律,假設節點在相同時間段有相同的相遇概率,根據節點的歷史相遇概率提出概率轉發機制的路由.文獻[16]將節點流行度和歸屬團體相結合,通過具有高流行度的節點來傳輸消息,提出了高傳輸成功率消息傳輸的路由算法.文獻[17]提出了一種基于區域朋友關系的機會路由算法.該算法利用節點的歷史接觸信息構造了節點親密度評價模型,進而利用節點的當前位置和親密關系傳輸數據.文獻[18]利用節點興趣提出了機會網絡興趣社團路由算法(ICR),該算法定義了節點興趣和消息興趣,通過節點興趣的相似性來劃分社團,然后通過節點同目標節點是否屬于同一個興趣社團來確定消息的轉發策略.

為了平衡節點能量消耗,研究者也提出了一些能量均衡的路由算法.文獻[19]綜合考慮消息擴散程度和節點剩余能量,并結合節點相遇概率預測方法,提出了能量有效的副本分布狀態感知路由機制.文獻[20]提出了一種自適應動態功率控制的節能路由算法.該算法通過改進基于接收信號強度指示值的節點測距機制,將功率控制范圍擴展到全部來減少節點能耗.文獻[21]提出基于節點探測的能量均衡機制.該機制先通過泊松分布模型得到有效的探測概率,然后,根據相關計算得出探測接觸數,最后,探測有效的能量均衡點.

本文在上述移動模型基礎之上,考慮節點的移動規律和節點的能量提出了基于社團的能量均衡路由算法,該算法分為社團內的消息傳輸策略和社團間的消息傳輸策略.本文提出的消息傳輸策略保證了消息的高效傳輸、均衡了節點能量和延長了網絡生存期.

3 移動模型

3.1 空間劃分

在該模型中,將整個區域S劃分為若干個子區域,稱為活動區.活動區是指在規定的時間內同一個社團的節點參與活動的區域.活動區的形狀設置為圓形.區域S內除去所有活動區外,剩余的區域為非活動區,用S0表示.如圖1所示,在區域S內包含三個活動區S1、S2和S3以及非活動區S0.因此,如果網絡中包含n個活動區域,即{S1,S2,…,Sn} 那么,區域S可以表示為:

S=S0∪S1∪S2∪…∪Sn

3.2 時間劃分

現有的節點移動模型主要考慮節點位置、方向、速度等特點,很少考慮節點移動的時空受限特性和周期特性.針對節點的這一社會特性,本文將仿真時間劃分為兩個時間段,即,tf時間段,和tr時間段.tf時間段為所有節點在仿真區域自由移動的時間;tr時間段為社團節點在活動區參加活動的時間.tr和tf交替發生具有周期特性.如圖2所示.

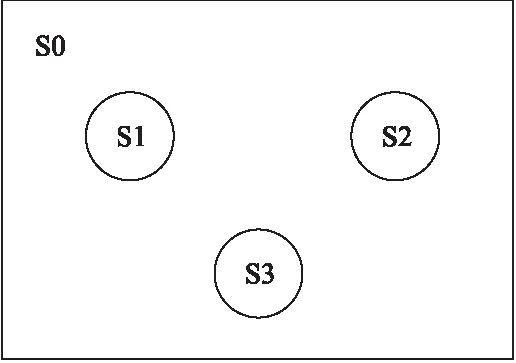
圖1 區域劃分示意圖Fig.1 Sketch map of regional division

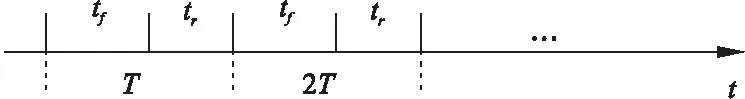
圖2 時間劃分示意圖
Fig.2 Sketch map of time division

從圖2中,可以得出,

T=tf+tr

(1)

t=kT

(2)

其中,t為仿真時間,T為仿真周期,k為周期數.

3.3 總體描述

移動模型共分為兩個階段,初始化階段和節點移動階段.在初始化階段:節點進行社團劃分和確定活動區.根據節點的相遇持續時間將節點劃分為不同的社團并為它們分配活動區,這些節點稱為受限節點.沒有被組成社團的節點稱為自由節點.社團的具體劃分步驟如下:

1.初始化節點i的社團為Cx;

2.當節點i與節點j相遇時,記錄兩個節點的相遇開始時間tstart和結束時間tend,通過節點的相遇開始時間和結束時間可以計算出節點i與節點j此次相遇的持續時間te=tend-tstart.將這兩個節點每次相遇持續時間累加,更新節點的持續相遇時間te

3.當節點i與節點j的持續相遇時間te大于閥值σ時,將節點j劃分到社團Cx

由Newman和Girvan提出的模塊度[22]來衡量社團劃分的好壞.其計算公式如下:

(3)

其中,Q為模塊度函數,其值越大社團劃分效果越好.A為鄰接矩陣,m為圖中總邊數,Pij代表節點i與節點j在模型中的邊數.若節點i與節點j屬于同一個社團,則δ(Ci,Cj)為1,否則為0.

由公式(3)可知,取不同的閥值將得到不同的社團結構,使得獲得不同的Q值.經試驗驗證,閥值σ為100秒為優值.按此方法將網絡中的n個節點劃分為m個社團.該社團劃分允許節點不屬于任何社團,此節點為自由節點在仿真時間內可以自由移動.社團個數是可變的.

隨著節點的移動和時間的變化,節點可能會選擇參加其他社團,網絡中的社團結構也會隨之變化,因此,在每個周期開始之前都會有1000秒的初始化階段來更新節點間的相遇持續時間,根據節點的相遇持續時間重新對節點進行社團劃分,這樣不僅符合節點的移動規律而且能降低算法的時間復雜度.

圖3 移動模型流程圖Fig.3 Flow chart of mobility model

在節點移動階段:社團節點在tf時間段在整個仿真區域自由移動,在tr時間段到指定的活動區參加活動;自由節點在整個仿真時間都保持自由移動.具體流程如圖3所示.

4 路由算法

在機會網絡中,根據節點的移動規律將節點劃分為不同的社團有利于提高消息的傳輸效率.若,源節點和目標節點處于同一個社團,可以在節點參加社團活動時將消息從源節點傳輸給目標節點,這樣不僅避免了消息在其他社團中擴散降低網絡資源,而且提高了消息傳輸成功率.若,源節點和目標節點不在同一社團,可以先利用即和源節點處于同一個社團又和目標節點處于同一個社團的中繼節點將消息帶到目標節點所在的社團,再通過社團內的消息傳輸機制,將消息傳輸給目標節點.若,源節點和目標節點有一個參與社團或都不參與社團,可以利用節點在自由移動時間段構建源節點與目標節點之間的消息傳輸路徑,進而傳輸消息.在此情況下使用社團內的消息傳輸機制.因此,該算法可分為社團內的消息傳輸機制和社團間的消息傳輸機制.

4.1 社團內的消息傳輸

PRoPHET算法是通過分析節點的移動行為,認為現實中的節點很可能不完全按照隨機的移動方式移動,而是基于某種重復行為模型,這種移動行為是可預測的.該算法定義了一個傳輸預測值來描述節點之間成功傳輸的概率,當兩個節點相遇時,節點更新自身的傳輸預測值,并利用該值決定是否轉發數據分組.由于社團內的節點相遇比較頻繁,相遇概率較高,如果直接使用該算法傳輸數據會使得社團內存在大量消息副本,浪費資源,同時該算法沒用考慮節點的剩余能量,如果節點的相遇概率很高但是剩余能量很少,那么也不利于消息傳輸.因此,本文將PRoPHET作相應的改進以適合社團內的消息傳輸.在消息轉發時選擇目標節點的一跳節點作為中繼節點轉發,同時考慮節點的相遇概率和剩余能量來決定是否轉發數據分組.這樣不僅保證了傳輸成功率,而且平衡了節點能量消耗.

網絡中的每個節點維護一個轉發概率向量表,用來存儲節點的轉發概率,節點的轉發概率的計算分為轉發概率更新和老化.

當節點i與節點j相遇時,節點間的相遇概率由公式(4)計算,

pm(i,j)=pm(i,j)old+(1-pm(i,j)old)×pinit

(4)

其中pinit為初始相遇概率為0.75.

節點剩余能量所占的比例pE,由公式(5)計算:

(5)

其中,Ec為節點的剩余能量,Ei為節點的初始總能量.

轉發概率由公式(6)計算.該公式保證了經常相遇的且剩余能量多的節點轉發概率更大.

p(i,j)=αpm(i,j)+(1-α)pE

(6)

其中α為權值因子,由實驗可知,α=0.75最為合適.

節點i和j在時間單元內沒用相遇,則其轉發概率逐漸老化,計算公式如(7)式所示.

p(i,j)=p(i,j)old×γk

(7)

其中,γ∈[0,1] 是一個初始化常數,k為經過的時間單元數.經試驗驗證,γ=0.98為最合適的常數.

故,社團內的消息傳輸策略為:當兩個節點相遇時,通過比較兩個節點的轉發概率來確定是否轉發數據分組.若相遇節點到目標節點的轉發概率大于當前節點到目標節點的轉發概率,則將消息轉發給相遇節點;否則,不轉發.同時,算法增加了ACK機制,當目標節點收到消息時,向網絡中發送ACK數據包響應消息,收到數據包的節點通過對比數據包的信息刪除該消息的冗余副本,這樣既能減少資源浪費,又能節約節點能量.

4.2 社團間的消息傳輸

社團間的消息傳輸的關鍵是找到連接社團的中繼節點,通過這些中繼節點構成社團間的連通路徑,從而完成社團間的消息傳輸.由于節點可能參與不同的社團,因此,存在一些節點即與源節點在同一個社團又和目標節點在同一個社團,可以通過這些節點建立社團之間的連接路徑.大量節點參與不同的社團可能存在多條連通社團間的路徑,找出這些路徑中的最佳路徑就可以完成社團間的消息傳輸.

如圖4所示,節點i要將消息傳給目標節點d具體過程如下:假設節點i屬于Cx社團,節點d屬于Cy社團,節點j即屬于Cx社團又屬于Cy社團.當社團Cx舉辦活動時,節點i將消息轉發給節點j,當社團Cy舉辦活動時,節點j會將消息帶入到社團Cy,這樣就建立了Cx→Cy之間的鏈路,通過這樣的連通鏈路就可實現社團之間的消息傳輸.由于這種連通鏈路可能有很多條,為了找出社團間的最佳路徑,本文定義了傳輸概率.

由于不同的社團舉辦活動的周期不同,可以通過周期來確定社團間的最優路徑.選擇頻繁參加活動的節點來傳輸消息.通過公式(8)將社團活動的周期轉化為效用值.

pt(Cy)=e-βTc

(8)

其中,Tc為節點參與社團活動的周期,β為保護因子,其取值與Tc有關,本實驗設置為0.001.

圖4 社團間的消息傳輸示意圖Fig.4 Sketch map of message transmission between community

社團間的傳輸概率可由公式(9)計算:

pm(Cy)=p(i,j)pj(Cy)

(9)

節點在移動過程中傳輸概率是不斷更新和老化的.當節點i與節點j建立社團間的連通鏈路時,通過公式(9)計算這條路徑的傳輸概率,如果新路徑的傳輸概率大于老路徑的傳輸概率,則更新傳輸概率.否則,不更新.

由于社團之間存在多條路徑,且這些路徑是隨著時間動態變化的,若通過節點j連接兩個社團之間的路徑一段時間內沒有更新,則其傳輸概率逐漸老化,由公式(10)計算:

pm(i,j)=pm(i,j)old×ηk

(10)

其中,η∈[0,1] 是一個初始化常數,經實驗仿真,η=0.98是較為理想的常數值.k是經過的時間單元個數.

故,社團間的消息傳輸策略為:消息在社團間轉發時,通過參與多個社團的節點建立社團之間的連接路徑.當節點遇到多個能到達目標社團的節點時,將消息轉發給傳輸概率高的節點,由該節點將消息帶到目標節點所在的社團,進而建立社團之間的最優路徑.通過這條路徑將消息從一個社團帶到另一個社團.達到社團間消息傳輸的目的.

5 實驗及結果分析

5.1 仿真環境設置

本文使用由芬蘭Nokia研究中心開發的開源仿真工具ONE(Opportunistic Network Environment)[23]對提出的EBRC算法進行仿真.仿真之前,先進行10000s的初始化以完成社團劃分,仿真參數如表1.

5.2 實驗結果及分析

基于上述參數和仿真場景,對CMOT[24],PRoPHET,Epidemic和本文提出的算法在節點個數、節點移動速度、節點緩存和消息TTL不同下進行了算法的傳輸成功率、平均時延、網絡負載的對比分析.最后,對比了不同算法的節點剩余能量.

5.2.1 節點數對路由算法的影響

實驗設置節點的平均移動速度為6m/s,節點緩存大小為10M,消息TTL為300min.其他參數如表1所示.仿真結果如圖5所示.圖5(a)表明,隨著節點密度的增加,EBRC算法和CMOT算法的變化趨勢基本一致,同時可以看出節點密度對這兩種算法的傳輸成功率影響不大.在仿真算法中EBRC傳輸成功率最高.原因分析:

PRoPHET算法和Epidemic算法沒

圖5 節點數對路由算法的影響Fig.5 Influence of node numbers on algorithms

有考慮節點的聚集特性和周期特性,因此消息的投遞范圍有限,傳輸成功率較低.CMOT雖然考慮了節點的聚集特性,但是并不適用于周期性聚集的移動模型,所以其傳輸成功率略低于EBRC算法.圖5(b)表明,隨著節點密度的增加,EBRC,CMOT,PRoPHET算法的平均時延在一定范圍內波動,整體變化不大,這說明節點密度對這3中算法的平均時延影響不大.相反,Epidemic算法的平均時延變化很大.同時可以看出,CMOT的平均時延略低于EBRC,這是因為EBRC算法在社團間主要依靠社團活動的周期來建立社團間的消息傳輸路徑,只有當社團有活動時,才可以傳輸消息.圖5(c)表明,隨著節點密度的增加,4中算法的網絡負載都在增加.EBRC算法具有最低的網絡負載.

5.2.2 節點平均速度對路由算法的影響

實驗設置節點的個數為150個,節點緩存大小為10M,消息TTL為300min.其他參數如上表所示.仿真結果如圖6所示.從圖6(a)可以看出,節點的平均移動速度對4中算法的傳輸成功率影響不大,且EBRC路由算法高于PRoPHET算法和Epidemic算法.圖6(b)表明,隨著節點平均移動速度的增加,4種算法消息的平均時延大大降低,這是因為,當移動速度大時,消息能更快的傳輸到目標節點,消息的平均延時會

降低.同時可以看出,當節點平均移動速度小于8m/s時,EBRC算法的平均延時表現較好.圖6(c)可以看出,隨著節點移動速度的增加,PRoPHET算法和Epidemic算法的網絡負載明顯增加,而EBRC算法和CMOT算法幾乎不變.EBRC算法的負載最低.

表1 仿真參數設置
Table 1 Simulation parameter setting

圖6 節點平均速度對路由算法的影響Fig.6 Influence of node average speed on algorithms

5.2.3 節點緩存大小對路由算法的影響

實驗設置節點的個數為150個,節點平均移動速度為6m/s,消息TTL為300min.其他參數如上表所示.仿真結果如圖7所示.圖7(a)表明,隨著節點緩存的增加4種算法的傳輸成功率都在增加,其中EBRC算法和CMOT算法傳輸成功率增加較快,PRoPHET算法和Epidemic算法增加較慢.同時可以看出,EBRC算法有最高的傳輸成功率.圖7(b)表明,節點緩存對Epidemic算法的平均時延幾乎沒有影響,而對EBRC算法和CMOT算法的平均時延影響較大.同時可以看出,EBRC算法適用于緩存比較小的節點,隨著緩存的曾加,EBRC算法的延遲表現不佳.圖7(c)表明,隨著節點緩存的增加,網絡負載隨之減少.且EBRC算法的網絡負載遠遠低于PRoPHET算法和Epidemic算法表現最佳.

5.2.4 消息TTL對路由算法的影響

圖7 節點緩存大小對路由算法的影響Fig.7 Influence of node cache size on algorithms

實驗設置節點的個數為150個,節點平均移動速度為6m/s,節點緩存為10M.其他參數如上表所示.仿真結果如圖8所示.

圖8 消息TTL對路由算法的影響Fig.8 Influence of TTL on algorithms

圖8(a)表明,隨著消息TTL的增加,EBRC算法和CMOT算法的傳輸成功率呈現增加后下降的趨勢變化,而PRoPHET算法和Epidemic算法的傳輸成功率呈下降趨勢.且EBRC算法的傳輸成功率最高.圖8(b)表明,當消息TTL小于200min時EBRC算法的平均延遲隨著消息TTL的增加而增加;當消息TTL大于200min時EBRC算法的平均延遲隨著消息TTL的增加幾乎不變.Epidemic算法的平均延遲最差.圖8(c)表明,隨著消息TTL的增加,4種算法的網絡負載明顯增加,EBRC算法具有較低的網絡負載.

5.2.5 節點剩余能量對比分析

實驗設置節點的個數為150個,節點平均移動速度為6m/s,節點緩存為10M,消息TTL為300min.其他參數如上表所示.仿真結果如圖9所示.

圖9表明,當仿真時間結束時,對于PRoPHET算法和Epidemic算法大部分節點的剩余能量為0,一部分節點剩余很多能量,網絡能量不均衡.CMOT算法有一部分節點剩余能量為0,且其他節點的剩余能量也相差較大,網絡能量不均衡.EBRC算法所有節點剩余能量相差不大,且沒有節點能量為0,網絡能量較均衡.這是因為,EBRC算法考慮了節點的剩余能量,讓剩余能量多的節點傳輸數據,剩余能量少的節點幾乎不會傳輸數據,因此,具有很好的能量利用,達到網絡能量均衡的效果.

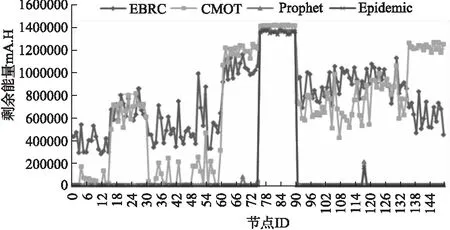
圖9 節點的剩余能量Fig.9 Residual energy of nodes

6 結 論

本文一方面根據機會網絡的移動特性結合社會網絡節點的社團和周期特性,提出了一種時空受限的移動模型,使得節點的移動更加符合具有社會特性實際場景.另一方面,在這種移動模型基礎之上,提出了基于社團的能量均衡路由算法.該算法在社團內考慮節點的相遇概率和節點剩余能量來轉發消息;在社團間充分利用節點移動的周期特性來尋找社團間的最佳路徑進行消息傳輸.仿真結果表明,該算法提高了消息的傳輸成功率,降低了網絡負載,同時也實現的網絡能量均衡.本文的移動模型具有一些約束條件,這于現實場景存在一定差距,需要進一步完善,EBRC算法僅僅通過周期來確定最優路徑,有一定的局限性,也需要相應的優化.