解決圓與其他知識點融合類題目的策略

黃海濤

一、借助圓內(nèi)接四邊形的外角、同弧所對的圓周角，可以將已知角轉(zhuǎn)化為其他的等角，利用直徑所對的圓周角、垂徑定理構(gòu)造直角三角形，是解決綜合三角函數(shù)類題目的常用方法

例1（2018·江蘇無錫）如圖1，四邊形ABCD 內(nèi)接于圓 O，AB=17，CD=10，∠A=90°，，求AD的長.

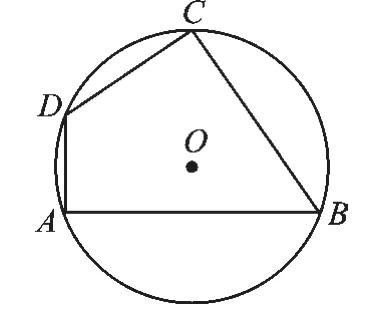
圖1

【解析】考點：圓內(nèi)接四邊形、三角函數(shù).四邊形ABCD為圓內(nèi)接四邊形，容易得到∠A=∠C=90°.如何把放在直角三角形中是解決問題的關(guān)鍵.結(jié)合四邊形ABCD為圓內(nèi)接四邊形，∠A=90°，容易想到構(gòu)造圓內(nèi)接四邊形的外角，將∠B放到直角三角形中.

【解答】解：如圖2，延長AD，BC交于點E.

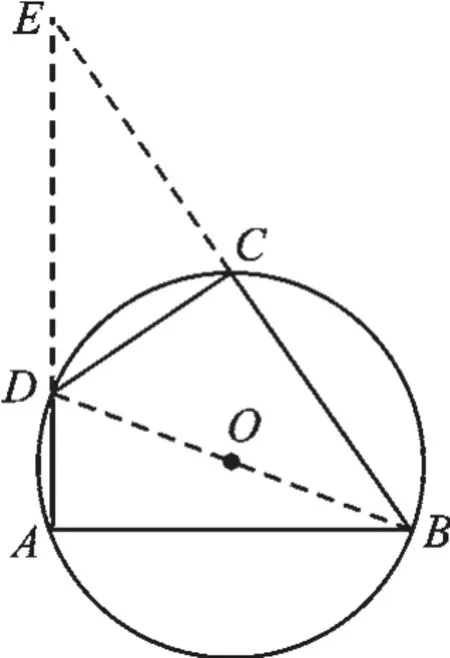
圖2

∵四邊形ABCD為圓內(nèi)接四邊形，

∴∠A=∠DCB=90°，∠B=∠EDC.

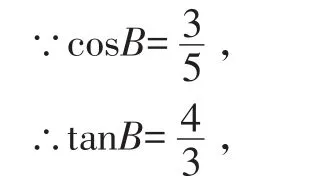
∴在直角三角形EAB中，

在直角三角形ECD中，

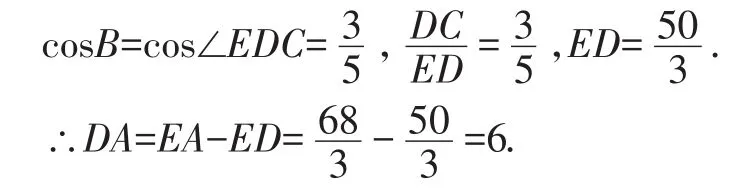
【點評】對于圓結(jié)合三角函數(shù)類問題，應(yīng)重點關(guān)注如何把已知的具體大小的角放入直角三角形中.

二、結(jié)合題目中的已知線段，利用同弧所對的圓周角、連接半徑形成的等腰三角形、圓內(nèi)接四邊形的外角等知識，發(fā)掘相似三角形，是解決圓與相似有關(guān)問題的實用技巧

例2（2018·四川成都）如圖3，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于點D，O為AB上一點，經(jīng)過點A，D的⊙O分別交AB，AC于點E，F(xiàn)，連接OF交AD于點G.

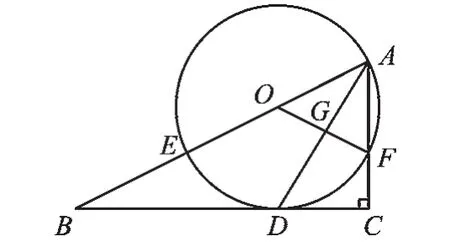
圖3

（1）求證：BC是⊙O的切線.

（2）設(shè)AB=x，AF=y，試用含x，y的代數(shù)式表示線段AD的長.

【解析】考點：圓、相似三角形.

（1）因為點D在圓上，因此，要證明圓的切線，只需連接半徑，證垂直即可.

（2）線段AB在△ABD和△ABC中，而線段AF不在直角三角形中，因此找△ABD的相似三角形是解決問題的關(guān)鍵.結(jié)合上一問得到的結(jié)論∠BAD=∠CAD，容易想到證明△ABD∽△ADF，此時只需證明∠ADF=∠B即可，要證∠ADF=∠B，只要用弧AF所對的圓周角∠AEF過渡一下，而連接EF后發(fā)現(xiàn)∠EFA=90°，易得EF‖AC，問題得到解決.

【解答】證明：（1）如圖4，連接OD.

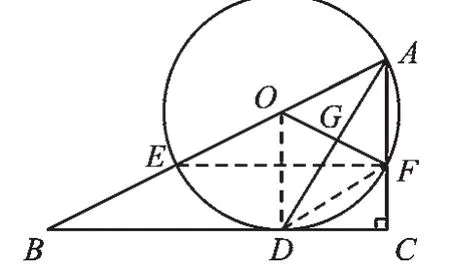
圖4

∵AD為∠BAC的角平分線，

∴∠BAD=∠CAD.

∵OA=OD，∴∠ODA=∠OAD，

∴∠ODA=∠CAD，∴OD‖AC，

又∵∠C=90°，∴∠ODC=90°，

∴BC是⊙O的切線.

解：（2）連接DF，EF.

∵AE是直徑，∴∠EFA=90°，

又∵∠C=90°，∴EF‖BC.

∴∠AEF=∠B，

∵在⊙O中，∠AEF與∠ADF對應(yīng)的弧相同，∴∠AEF=∠ADF，

∴∠ADF=∠B，

又∵∠BAD=∠CAD，

∴△ABD∽△ADF，

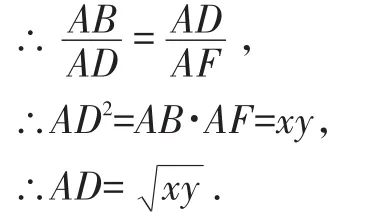
【點評】圓中線段間的數(shù)量關(guān)系如不涉及具體數(shù)值的計算，利用相似發(fā)掘乘積關(guān)系是常用方法，根據(jù)具體線段找相似三角形是比較有效的技巧.

三、對于圓中和弦長有關(guān)的計算問題，借助垂徑定理，作弦心距，連半徑，構(gòu)造直角三角形，用勾股定理解決線段的長度問題，是圓綜合勾股定理類題目的主要解題策略

例3（2018·江蘇南京）如圖5，在矩形ABCD中，AB=5，BC=4，以CD為直徑作⊙O.將矩形ABCD繞點C旋轉(zhuǎn)，使所得矩形A′B′CD′的邊A′B′與⊙O相切，切點為E，邊CD′與⊙O相交于點F，則CF的長為

圖5

【解析】考點：圓、勾股定理.如圖6，點E是⊙O的切點，連接OE，得到垂徑，而弦長問題往往又需要用垂徑定理來解決，OE垂直于A′B′，A′B′‖CD′正好巧妙地構(gòu)造了用勾股定理處理弦長問題所需的直角三角形，連接EO并延長交CF于點H，問題得解.

【解答】解：連接EO并延長交CF于點H.

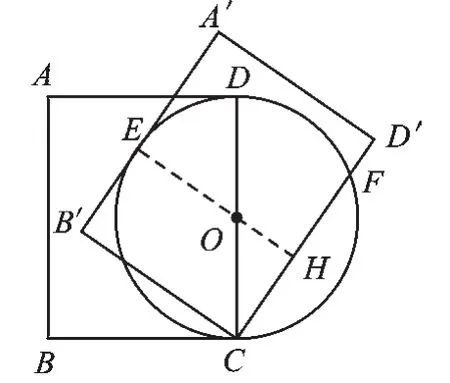
圖6

∵A′B′與⊙O相切于點E，

∴OE⊥A′B′，

又∵A′B′‖CD′，∴OH⊥CD′，

∴CH=HF.

【點評】解決此類弦長問題的切入點就是利用垂徑定理構(gòu)造直角三角形.而如果先作了垂直，連接了OE，是比較容易發(fā)現(xiàn)E、O、H三點共線的.雖然對于同學(xué)們而言證明三點共線不常見，但連好線后再仔細分析題目中的矩形對邊平行條件，是不難得到連接EO并延長這個輔助線作法的.

四、解決圓與方程、函數(shù)等知識點融合的綜合題時，用圓中半徑相等、直角三角形的勾股定理建立數(shù)量間的等量關(guān)系，是解決問題的必要途徑

例4（2018·山東濱州）如圖7，在平面直角坐標系中，圓心為P（x，y）的動圓經(jīng)過點A（1，2）且與x軸相切于點B.

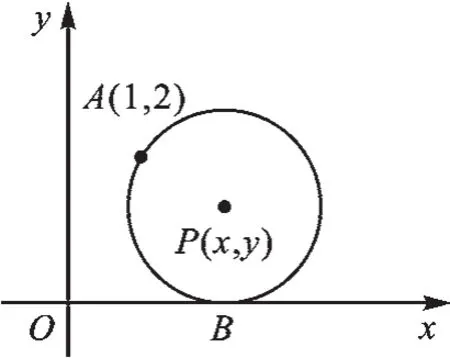
圖7

（1）當(dāng)x=2時，求⊙P的半徑.

（2）求y關(guān)于x的函數(shù)解析式，請判斷此函數(shù)圖像的形狀，并在圖8中畫出此函數(shù)的圖像.

圖8

（3）請類比圓的定義（圓可以看成是到定點的距離等于定長的所有點的集合），給（2）中所得函數(shù)圖像進行定義：此函數(shù)圖像可以看成是到_______的距離等于到_______的距離的所有點的集合.

（4）當(dāng)⊙P的半徑為1時，若⊙P與（2）中所得函數(shù)圖像相交于點C，D，其中交點D（m，n）在點C的右側(cè)，請利用圖8，求cos∠APD的大小.

【解析】考點：圓、勾股定理、二次函數(shù).

（1）由題意得到AP=PB，求出y的值，即為⊙P的半徑.

（2）利用兩點間的距離公式，根據(jù)AP=PB，確定出y關(guān)于x的函數(shù)解析式，畫出函數(shù)圖像即可.

（3）類比圓的定義描述此函數(shù)定義即可.

（4）畫出相應(yīng)圖形，求出m的值，進而確定出所求角的余弦值即可.

【解答】解：（1）如圖9，由x=2，得到P（2，y），連接AP，PB.

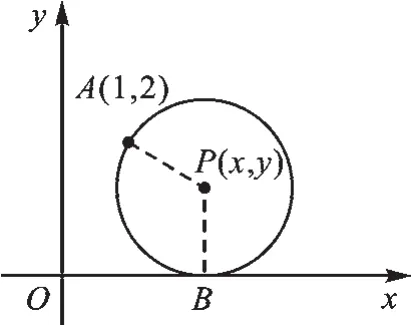
圖9

∵圓P與x軸相切，

∴PB⊥x軸，即PB=y，

（2）同（1），由AP=PB，

得到（x-1）2+（y-2）2=y2，

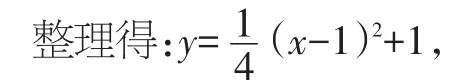
即y關(guān)于x的函數(shù)圖像為開口向上的拋物線，畫出函數(shù)圖像，如圖10所示；

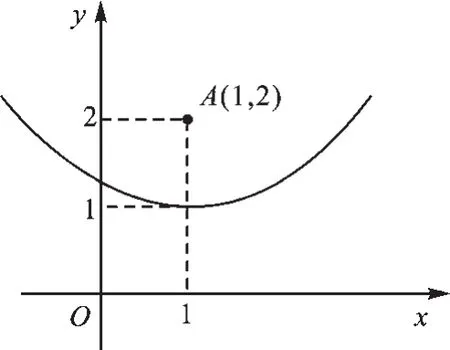
圖10

（3）給（2）中所得函數(shù)圖像進行定義：此函數(shù)圖像可以看成是到點A的距離等于到x軸的距離的所有點的集合.故答案為：點A；x軸.

（4）如圖11，連接CD，連接AP并延長，交x軸于點F.

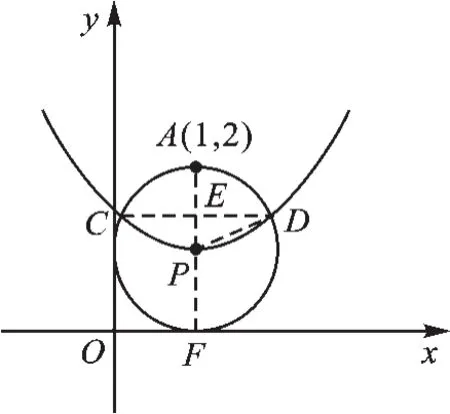
圖11

【點評】此題屬于圓的綜合題，涉及的知識有：兩點間的距離公式、二次函數(shù)的圖像與性質(zhì)、圓的性質(zhì)、勾股定理，用勾股定理建立x，y的等量關(guān)系是解本題的關(guān)鍵.

在解決與圓有關(guān)的綜合題時，除了要熟悉圓的基本概念、基本圖形，更應(yīng)該抓住圓中的一些隱含條件，如“同弧所對的圓周角相等”“半徑相等”等，注意知識點間的整合，滲透轉(zhuǎn)化的思想、數(shù)形結(jié)合的思想、方程的思想、分類討論的思想以及變化中的不變量等觀點，提高綜合運用知識的能力.