模糊一致集

李 輝，姜廣浩，劉東明

(淮北師范大學數學科學學院，安徽淮北 235000)

1 研究背景

自1965年Zadeh引入模糊集的概念[1]以來，眾多數學學者對于模糊數學的研究已取得了豐碩的成果，其中對模糊理想的定義就出現多種形式，本文采用其中一種模糊理想的定義方式.白仲林[2]給出了偏序集上一致偏序集的定義，使偏序集得以豐富.Yuan B[3]引入了模糊理想的概念，研究了模糊格上的模糊理想和模糊濾子.姜廣浩[4]給出了偏序集上局部極大理想的定義，并探討了局部極大理想的一些性質.肖璨[5]提出了模糊集在分配格上的一個內部刻畫，給出了模糊主理想、模糊次極大理想等定義,并考察了幾類模糊理想之間的關系.本文首先在一致集的基礎上，結合模糊偏序集和模糊理想的相關知識，給出模糊一致集和模糊一致完備集的定義，并研究它們的相關性質.其次，引入模糊一致理想和極大模糊一致理想的概念，討論模糊理想與模糊一致理想的關系，給出若干等價條件，并證明極大模糊一致理想的存在性.

2 預備知識

給出如下定義[1-3]：

定義2.1 (i)設X是偏序集，Y?X稱為X的一致集，若?x,y∈Y，存在z∈X，使得x≤z且y≤z；(ii)對偏序集上X的任意一致集都存在最小上界，則稱X是一致完備的.

定義2.2 設X是非空偏序集，A:X×X→[0,1]為映射，其中[0,1]為單位閉區間，稱A是X上的一個模糊偏序關系，若A滿足：(i)自反性：?x∈X，A(x,x)=1；(ii)傳遞性：?x,y,z∈X，A(x,y)∧A(y,z)≤A(x,z)；(iii)反對稱性：?x,y∈X，A(x,y)>0，A(y,x)>0?x=y，則稱偶對(X,A)為模糊偏序集，簡稱模糊集.

定義2.3 設(X,A)為模糊集，Y?X為子集，u∈X，若對?x∈Y有A(x,u)>0，則稱u為Y的一個上界，若對Y的任意上界y∈Y都有A(u,y)>0，則稱u為Y的上確界；若有A(u,x)>0，則稱u為Y的一個下界，若

對Y的任意下界v都有A(v,u)>0，則稱u為Y的下確界.Y的上確界記為supY,用符號表示為∨Y，下確界記為infY，用符號表示為∧Y.若對?x,y∈X，都有A(x,y)>0或A(y,x)>0，則稱A為模糊全序關系，(X,A)為模糊全序集.

定義2.5 設(X,A)為模糊格，Y?X為子集，(i)若x∈X,y∈Y，且A(x,y)>0時，有x∈Y；(ii)若x,y∈Y，有x∨y∈Y，則稱Y為模糊理想.全體模糊理想記作FIdl(L).

注2.1 若Y?X為模糊格(X,A)的一個模糊理想，則(Y,B)為(X,A)的模糊并半格.

3 主要結果

定義3.1 設(X,A)為模糊偏序集，Y?X為非空分明子集，若?x,y∈Y，存在z∈X，使得A(x,z)>0,A(y,z)>0，則稱Y為模糊集(X,A)上的一個模糊一致集，(X,A)上的全體模糊一致集記為FU(X).

例3.1 設X={a,b,c},Y={a,b}，規定A(a,c)>0,A(b,c)>0，則Y為模糊一致集.若還有A(a,b)>0或A(b,a)>0,則稱(X,A)為模糊全序集.

定義3.2 若模糊集(X,A)中的每個模糊一致集都存在上確界，則稱模糊集(X,A)是模糊一致完備的.若對?Y∈FU(X)，?x,y∈Y時x∧y,x∨y都存在，則稱(X,A)為模糊一致格.

注3.1 每個模糊一致格都是模糊一致完備的，但模糊一致完備集不一定是模糊一致格.因為對?x,y∈Y，x∧y不一定存在.

注3.2 設(X,A)為模糊一致格，則(X,A)為模糊格.

證明 設(X,A)為模糊一致完備集，Y∈FU(X)，則對?x,y∈Y?X，x∧y,x∨y都存在，故(X,A)為模糊格.

上述推論反過來不成立，即若(X,A)為模糊格，但(X,A)未必為模糊一致格.

例3.2 在圖1中，設模糊格L={a,b,c,d,e}，I={a,b,c,d}為模糊一致集，但a∨b=e?I,即I不為模糊一致格.

圖1 例3.2示意圖

定理3.1 設(X,A)為模糊格，D,F∈FU(X)，若D∩F≠?，則D∩F為模糊一致集.

證明 設(X,A)為模糊格，D,F∈FU(X)，令W=D∩F，由于(X,A)為模糊格，故對?x,y∈X，x∧y都存在.對?x,y∈W，即x,y∈D∩F，可知x,y∈D且x,y∈F.由D,F為模糊一致集，故存在z∈X使得A(x,z)>0,A(y,z)>0，故W為模糊一致集，即D∩F為模糊一致集.

定義3.3 設(X,A)為模糊偏序集，若(1)I∈FU(X)；(ii)若x∈X,y∈I，當A(x,y)>0時，有x∈I，則稱I為模糊集(X,A)的模糊一致理想.全體模糊一致理想記作FUIdl(L).

定理3.2 設(X,A)為模糊格，若I∈FIdl(L)，則I∈FUIdl(L).

證明 設(X,A)為模糊格，I∈FIdl(L)，x∈X,y∈I，A(x,y)>0有x∈I，且x,y∈Y，有x∨y∈Y，令z=x∨y，故z∈I?X,又有A(x,z)>0,A(y,z)>0，即對?x,y∈I時，存在z∈X,使得A(x,z)>0,A(y,z)>0，故I為模糊一致理想.

推論3.2 定理3.2的逆定理不成立，即I為模糊一致理想，但I未必是模糊理想.

例如在圖1中I為模糊一致理想，但不是模糊理想.因為雖然a∈I,b∈I，但a∨b?I，故I不為模糊理想.

在何條件下模糊理想是模糊一致理想呢？下面給出一個等價條件.

命題3.1 設(X,A)為模糊一致完備集，I?X，則I為模糊一致理想?I為模糊理想.

證明 必要性證明.設(X,A)為模糊一致完備集，I為其上的一個模糊一致理想.?x∈X,y∈I,A(x,y)>0，有x∈I，又由(X,A)模糊一致完備，故x∨y存在，且x∨y∈I,故I為模糊理想.

充分性證明.設I∈FIdl(L),由定理3.2可知I∈FUIdl(L).故充分性成立.

定理3.3 設(X,A)為模糊集，Y為其上的模糊一致集，則↓Y={x∈X:?y∈Y,A(x,y)>0}為一個模糊一致理想.

證明 (i)設c∈↓Y，d∈X，使得A(d,c)>0，由Y為模糊一致集，故存在x∈Y使得A(c,x)>0，由傳遞性A(d,x)>0，可知d∈↓Y.

(ii)設x,y∈↓Y，于是存在a,b∈Y，使得A(x,a)>0,A(y,b)>0，進而A(x,a∨b)>0，A(y,a∨b)>0，令z=a∨b，于是對任意的x,y∈↓Y，存在z∈X,使得A(x,z)>0,A(y,z)>0，故↓Y為模糊一致集.綜上↓Y為一個模糊一致理想.

注3.3 若將定理3.3中(X,A)為模糊集改為模糊一致完備集，其余條件不變，則↓Y為一個模糊理想.這是因為在證明(ii)中若(X,A)為模糊一致完備，則z∈↓Y，故↓Y為模糊理想.

命題3.2 設(X,A)為模糊格，Y為(X,A)上的一個模糊一致理想，則↓Y?↓supY.

證明 由Y為模糊一致理想，故對?x,y∈Y，?z∈X，使得A(x,z)>0，A(y,z)>0.取z=supY,即?x,y∈Y，x,y∈↓supY，故↓Y?↓supY.

命題3.3 設L為模糊偏序集，Y為它的模糊一致理想，則對?x∈Y,有Y=∪↓x，其中↓x為模糊主理想.

定理3.4 設Y是模糊偏序集(X,A)的一個模糊一致理想，且x∈XY，令I=∪{↓(x∨a):a∈Y}，則I是(X,A)的一個模糊理想，且Y?I.

證明 (i)任取b1,b2∈I，x∈XY，則存在a1,a2∈Y，使得A(b1,x∨a1)>0，A(b2,x∨a2)>0，故A(b1∨b2,(x∨a1)∨(x∨a2))>0，即A(b1∨b2,x∨(a1∨a2))>0.令z=x∨(a1∨a2)，則b1∨b2∈↓z.

(ii)下證z∈I.事實上，對任意a∈Y，有I=∪(↓(x∨a))=↓(∪(x∨a)).對任意a1,a2∈Y，有x∨(a1∨a2)∈∪(x∨a)，即z∈∪(x∨a)，進而z∈↓(∪(x∨a))，故z∈I.因此，對任意b1,b2∈I，b1∨b2∈I,故I為一個模糊理想.

定義3.4 設(X,A)為模糊偏序集，Y為(X,A)中的模糊一致理想，若?x∈X，使得Y在不包含x的模糊一致理想中極大，則稱Y為(X,A)的一個極大模糊一致理想.即若x?Y,x∈I∈FU(X)且Y?I，則Y=I.

定理3.5 設(X,A)為模糊格，Y為(X,A)的模糊一致理想，對?a?Y，則必存在關于a的極大模糊一致理想M，使得a?M且Y?M.

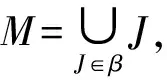
注3.4 在圖1中{a,b,c,d}，{a,c,d}，{b,c,d}均為關于元素e的極大模糊一致理想，g0gggggg是關于元素c的極大模糊一致理想，但{c,d}不為極大模糊一致理想，因為{c,d}包含于{a,c,d}和{b,c,d}中.

注3.5 根據模糊一致集的定義，若z?Y，則模糊一致理想Y是關于z的極大模糊一致理想；若z∈Y，則模糊一致理想Y是模糊理想.