基于貝葉斯理論框架的傳感器選擇算法

郭軍軍 韓崇昭

隨著傳感器技術(shù)和雷達量測技術(shù)的飛速發(fā)展,傳感器的種類和數(shù)目變得越來越豐富,因此在目標跟蹤場景中,我們可以使用大量的傳感器同時對空間目標進行跟蹤和檢測.近年來,多傳感器甚至大規(guī)模傳感器網(wǎng)絡(luò)目標跟蹤技術(shù)得到了越來越廣泛的應(yīng)用[1?3].

使用大規(guī)模傳感器網(wǎng)絡(luò)對空間目標進行跟蹤時,傳感器由于受所處環(huán)境的影響,例如,量測空間中可能存在少量雜波干擾、傳感器存在系統(tǒng)偏差等.特別是對于大規(guī)模傳感器網(wǎng)絡(luò),幾乎不可避免的傳感器系統(tǒng)偏差干擾,給傳感器網(wǎng)絡(luò)數(shù)據(jù)融合帶來了很大的影響.因此當外界環(huán)境存在量測擾動時,研究傳感器網(wǎng)絡(luò)目標跟蹤問題是非常有意義的.

傳感器對空間目標進行量測時,傳感器自身固有的系統(tǒng)偏差通常是需要考慮的,一般而言,傳感器恒定的系統(tǒng)偏差很容易進行估計.目前國內(nèi)外已經(jīng)有很多學(xué)者提出了許多的恒定系統(tǒng)偏差估計算法,例如,在地心地固(Earth-centered Earth-fixed,ECEF)量測坐標系中,文獻[4]根據(jù)雷達的量測原理,提出了一種基于最小二乘估計法的傳感器系統(tǒng)偏差估計算法;文獻[5]提出了一種基于貝葉斯框架下的傳感器系統(tǒng)偏差估計和航跡–航跡融合算法;文獻[6]提出了一種基于期望最大化的聯(lián)合傳感器系統(tǒng)偏差估計、數(shù)據(jù)關(guān)聯(lián)和數(shù)據(jù)融合算法;文獻[7]提出了一種基于偽量測的傳感器偏差估計和數(shù)據(jù)融合算法.

然而不幸的是,由于外界環(huán)境的擾動,傳感器還可能存在偶然出現(xiàn)的未知系統(tǒng)偏差,即為偶發(fā)性的系統(tǒng)偏差[8].如果我們不考慮這部分系統(tǒng)偏差,很可能會導(dǎo)致傳感器對空間目標的跟蹤精度降低.目前我們主要有兩種思路來解決這種偶發(fā)性的系統(tǒng)偏差問題.1)對這種偶發(fā)性的系統(tǒng)偏差進行估計和補償,例如,文獻[9]提出了一種基于廣義似然比檢驗(Generalized likelihood ratio test,GLRT)的系統(tǒng)偏差估計和目標跟蹤算法,即同時對這部分未知系統(tǒng)偏差出現(xiàn)的時刻和偏差大小進行估計,然后使用補償后的量測值進行數(shù)據(jù)融合.然而偏差估計誤差又不可避免地會對目標跟蹤精度產(chǎn)生影響;2)從野值點檢測和剔除的角度對該問題進行解決.目前廣泛采用的野值點檢測算法有最小二乘估計法[10]、多項式外推擬合法[11]、差分檢測算法[12]等.然而上述野值點檢測算法都依賴前幾個時刻的歷史數(shù)據(jù).不同于上述野值點剔除方法,近年來國內(nèi)外許多學(xué)者又提出了很多基于多傳感器融合的野值點檢測和融合算法,例如,文獻[13]提出了兩種基于量測殘差和基于航跡關(guān)聯(lián)方法的野值點檢測和融合算法;文獻[14]通過構(gòu)造各個信源的殘差序列來對野值點進行檢測并且對量測結(jié)果進行修正等.類似于野值點的檢測和剔除思想,本文試圖用傳感器選擇的思路來處理該問題,即根據(jù)傳感器網(wǎng)絡(luò)獲得的全部量測數(shù)據(jù),對傳感器資源進行合理的管理,僅僅選擇不存在偶發(fā)性系統(tǒng)偏差的傳感器進行數(shù)據(jù)融合.

傳感器選擇算法[15?17],作為一種非常有效的傳感器網(wǎng)絡(luò)量測數(shù)據(jù)處理方法,近年來得到了越來越廣泛的應(yīng)用.傳感器選擇算法僅僅只選擇量測結(jié)果中跟蹤結(jié)果較好的數(shù)據(jù)進行融合,同時又不需要消耗更多的量測資源.因此不僅能夠提高量測資源的使用效率,還能有效提升整個傳感器網(wǎng)絡(luò)的跟蹤精度以及目標跟蹤的穩(wěn)定性.

目前國內(nèi)外許多學(xué)者已經(jīng)提出了很多基于傳感器選擇的目標跟蹤算法.傳感器選擇算法通常的處理思路為:首先給定一個傳感器網(wǎng)絡(luò)的優(yōu)化準則,然后根據(jù)這個準則進行優(yōu)化,從而得到傳感器網(wǎng)絡(luò)的選擇方案.例如,文獻[18]和文獻[19]分別使用后驗克拉美–羅下界和克拉美–羅下界作為優(yōu)化準則來實現(xiàn)傳感器網(wǎng)絡(luò)的在線選擇和數(shù)據(jù)融合;文獻[20]和文獻[21]將傳感器選擇問題轉(zhuǎn)化為一個組合優(yōu)化問題,然后使用交叉熵(Cross-entropy)優(yōu)化準則來實現(xiàn)傳感器選擇和數(shù)據(jù)融合;文獻[22]和文獻[23]使用傳感器網(wǎng)絡(luò)最終估計誤差的協(xié)方差矩陣的跡作為優(yōu)化準則來實現(xiàn)傳感器網(wǎng)絡(luò)的選擇和信息融合;類似地,文獻[24]將狀態(tài)估計中的置信橢圓的大小作為優(yōu)化準則來進行傳感器選擇;為了有效降低傳感器網(wǎng)絡(luò)的數(shù)據(jù)傳輸量,文獻[25]將大規(guī)模傳感器網(wǎng)絡(luò)分解為若干個較小的傳感器子網(wǎng)絡(luò),然后再基于克拉美–羅下界的優(yōu)化準則[26]進行傳感器選擇.通過分割傳感器網(wǎng)絡(luò),使得傳感器網(wǎng)絡(luò)的數(shù)據(jù)傳輸量大大降低.不同于上述所有的傳感器選擇算法,本文提出了一種全新的基于貝葉斯理論框架下的傳感器選擇算法,通過極大化基于當前時刻全部信息量的條件概率密度函數(shù)的對數(shù)似然函數(shù)來獲得傳感器網(wǎng)絡(luò)的傳感器選擇方案,屬于傳感器選擇問題的一種全新的求解思路.而且本文提出的傳感器選擇算法,考慮了量測空間的少量雜波干擾和由于環(huán)境干擾引起的量測偏差.因此,本文提出的傳感器選擇算法可以更加廣泛地應(yīng)用于多傳感器目標跟蹤場景中.

本文基于貝葉斯(Bayes)框架,提出了一種基于傳感器選擇的傳感器網(wǎng)絡(luò)目標跟蹤算法.具體思路為,1)在Bayes框架下,求解基于當前時刻全部信息量的條件概率密度函數(shù)的對數(shù)似然函數(shù),并且根據(jù)不同的優(yōu)化目標,推導(dǎo)出傳感器選擇的目標函數(shù);2)根據(jù)優(yōu)化準則,求出對應(yīng)的傳感器選擇方案,并且對傳感器網(wǎng)絡(luò)進行管理;3)對所選擇的傳感器進行數(shù)據(jù)融合,獲得傳感器網(wǎng)絡(luò)對空間目標的跟蹤結(jié)果.

1 問題描述

1.1 基本假設(shè)以及符號定義

文中的一些基本假設(shè)以及用到的符號如下:

1）假設(shè)

a)大量離散分布的傳感器同時對空間目標進行跟蹤,且各個傳感器獨立進行量測;

b)空間中不同目標之間是相互獨立的;

c)由于受外界環(huán)境的影響,傳感器可能存在偶然出現(xiàn)的未知系統(tǒng)偏差;

d)傳感器的量測空間存在少量量測雜波的干擾,某一時刻傳感器獲得的所有量測值中,對每個目標至多有一個是真實的量測,其余的都是雜波,雜波與真實量測獨立,且雜波之間也是相互獨立的.

2)符號定義

a)Yts,k:k時刻,傳感器s∈{1,···,n}對目標t∈{1,···,m}的有效量測向量的集合;

b)Yks:k時刻,傳感器s對空間所有目標的有效量測的集合,且Yks={Yts,k|t=1,···,m};

c)Yk:k時刻,空間所有n個傳感器對空間所有m個目標的有效量測集合,且,···,n};

e)Xk:k時刻,空間所有m個目標的狀態(tài)向量的集合,且.

1.2 目標運動方程和量測方程

不妨假設(shè)n個傳感器同步地對空間中的m個運動目標進行監(jiān)測.目標t∈{1,···,m}的運動模型可以描述為

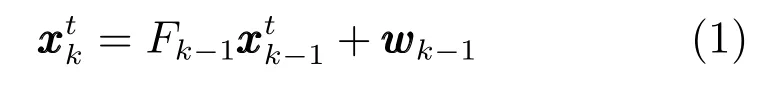
傳感器s∈{1,···,n}對空間目標t的量測方程可以表示為

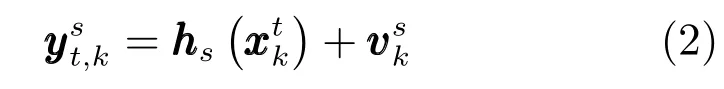
然而,傳感器在量測過程中,難免會受到外界環(huán)境的干擾,例如:1)少量量測雜波的干擾.量測雜波假設(shè)為:傳感器量測空間中,雜波數(shù)量服從密度為λ的泊松分布,雜波在量測空間中均勻分布,且雜波量測之間相互獨立.2)傳感器可能存在偶然出現(xiàn)的未知系統(tǒng)偏差.

因此,k時刻,傳感器s獲得的量測向量的集合可以表示為

2 基于Bayes理論的傳感器選擇算法

在大規(guī)模傳感器網(wǎng)絡(luò)目標跟蹤中,本文提出了一種基于Bayes理論的傳感器選擇算法.

2.1 獲取有效量測向量的集合

不妨假設(shè)k?1時刻,傳感器網(wǎng)絡(luò)對空間目標t的估計結(jié)果為, 類似于概率數(shù)據(jù)關(guān)聯(lián)(Probability data association,PDA)算法[27],k時刻傳感器s對空間目標t的有效量測集合Yts,k為

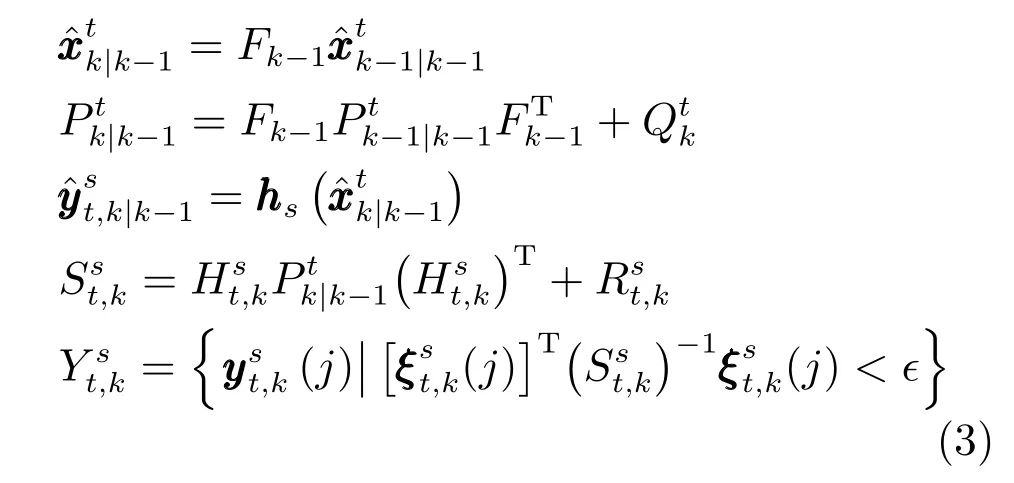
其中,∈為門限閾值(Gate threshold),且

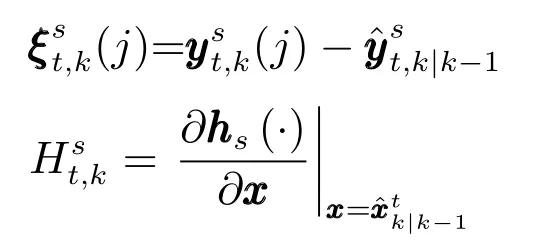
因此,k時刻,傳感器網(wǎng)絡(luò)對空間所有目標的有效量測集合可以表示為,t∈{1,···,m}}.

2.2 傳感器選擇的目標函數(shù)

不失一般性,不妨假設(shè)k?1時刻傳感器網(wǎng)絡(luò)對空間所有目標的跟蹤估計結(jié)果. 我們定義空間所有目標的狀態(tài)向量為,同時我們定義lks為傳感器s的選擇指示函數(shù),lks=1表示k時刻傳感器s被選中;反之lks=0表示k時刻傳感器s未被選中,即為

因此,k時刻傳感器網(wǎng)絡(luò)的選擇指示函數(shù)可以表示為Lk={lks|s=1,···,n}.

根據(jù)第2.1節(jié),可以很容易求得傳感器s對空間目標t的有效量測集Yts,k,同時為了建立Yts,k與空間目標t的關(guān)聯(lián)關(guān)系,我們定義Φst,k為有效量測集合Yts,k對空間目標t的關(guān)聯(lián)向量,且

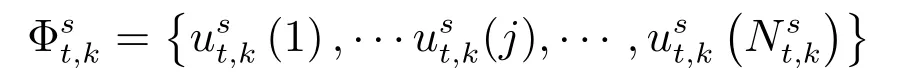
其中,Nts,k為k時刻,傳感器s對空間目標t的有效量測值的個數(shù).對于為量測向量對空間目標t的關(guān)聯(lián)變量,且滿足

為了保持公式推導(dǎo)過程中的簡潔性,定義

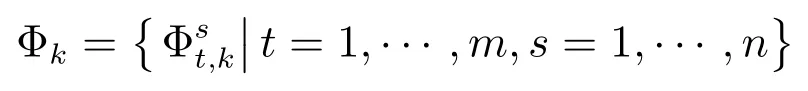
其中,Φk表示傳感器網(wǎng)絡(luò)中所有傳感器對空間所有目標關(guān)聯(lián)向量的集合.

根據(jù)Bayes公式,k時刻,在ρk?1的條件下,基于傳感器網(wǎng)絡(luò)當前全部量測信息的條件概率密度函數(shù)p(Xk,Φk,Yk|Lk,ρk?1) 可以表示為

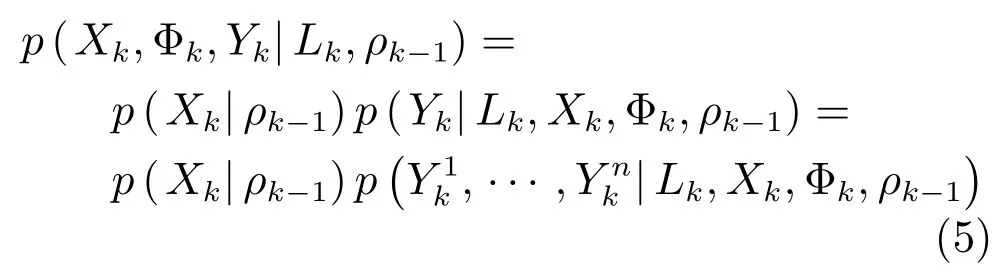
本文假設(shè)m個空間目標之間相互獨立,且各個傳感器之間是獨立量測的,因此式(5)等價為

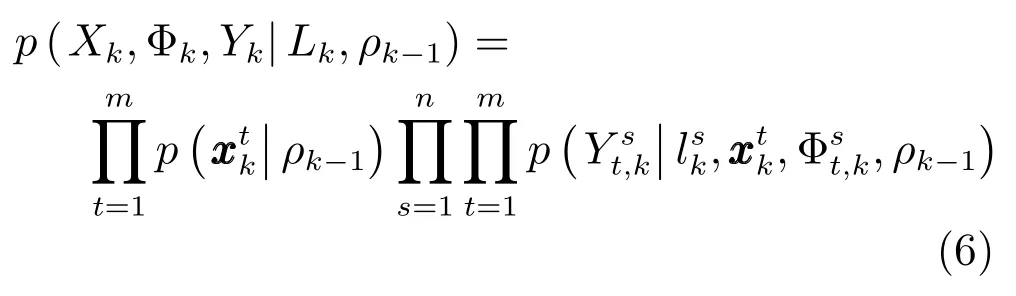
式(6)兩邊取對數(shù),即

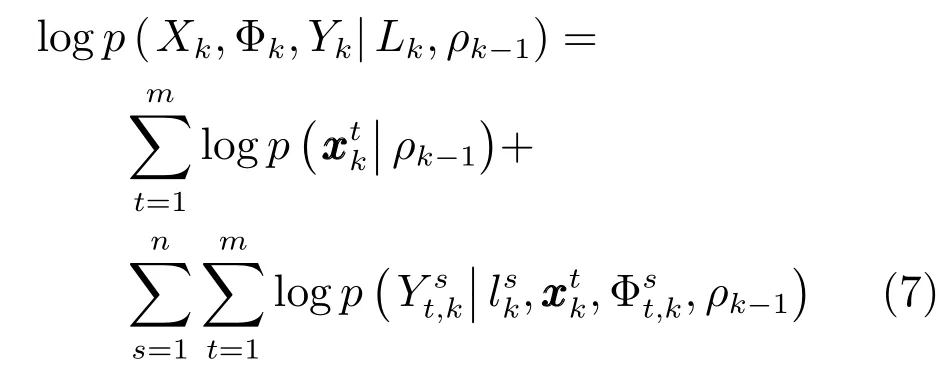
我們定義

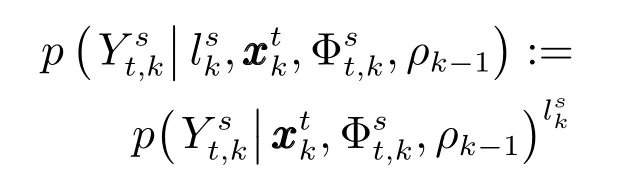
如果k時刻,傳感器s未被選中,即lks=0,此時;反之,傳感器s被選中,即,此時.

因此,可得

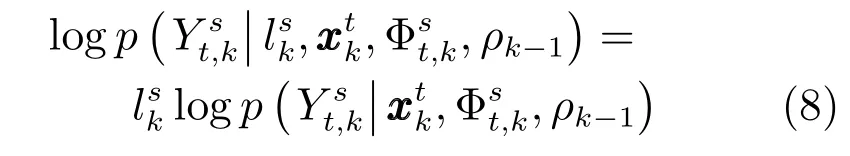
根據(jù)本文中的假設(shè),可知傳感器s對空間目標t的有效量測集合Yts,k中的各個量測值之間是條件獨立的,因此可得

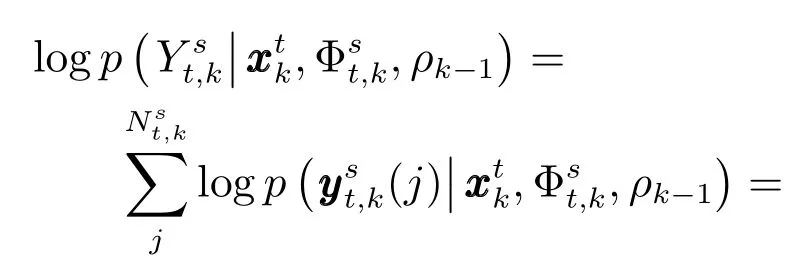
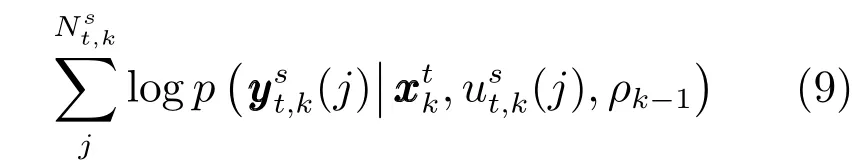
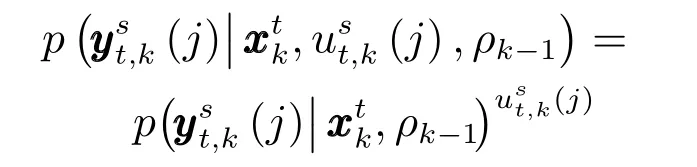
因此,式(9)可以等價為

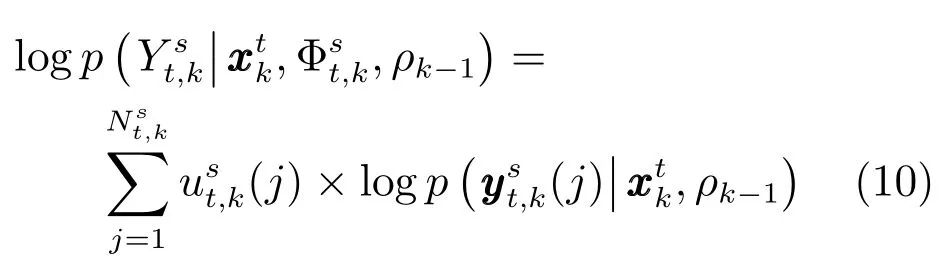
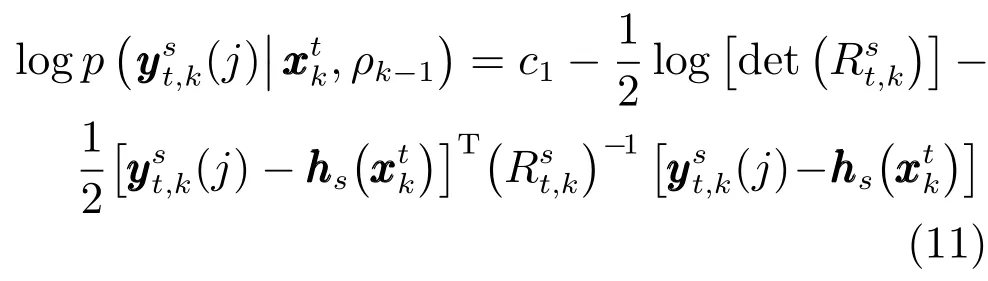
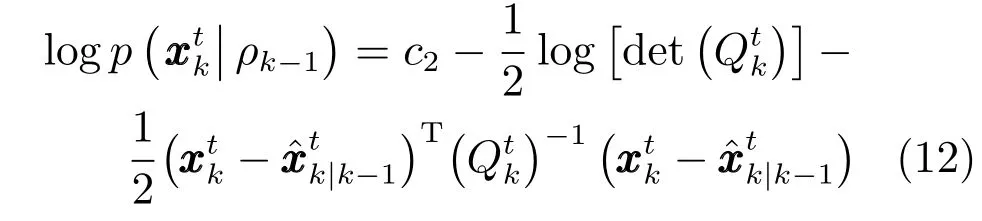
其中,c1,c2都為已知參數(shù).

將式(8),(9)和(12)代入式(7),可得式(13),其中,c3為已知參數(shù).

然后對該對數(shù)似然函數(shù)(式(13))求條件期望,得到傳感器選擇的目標函數(shù).

首先,基于全部傳感器量測信息Yk,定義目標狀態(tài)向量的條件期望和條件協(xié)方差矩陣分別為

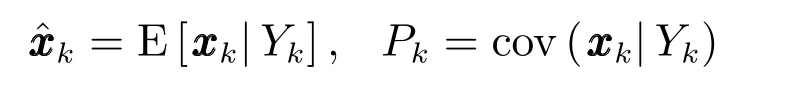
因此,全部量測值Yk條件下,式(13)對空間目標狀態(tài)向量xk的條件期望,得到當前k時刻傳感器選擇的目標函數(shù),即

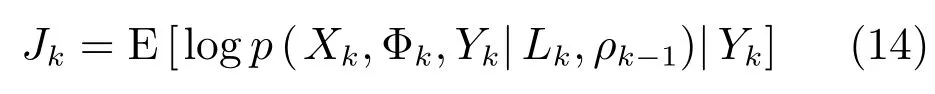
由于式(13)中,Item1項與傳感器量測無關(guān),因此求解傳感器選擇的目標函數(shù)時只考慮Item2項,即

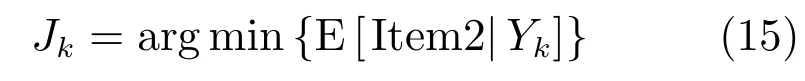
求解Item2項的條件期望時,可知

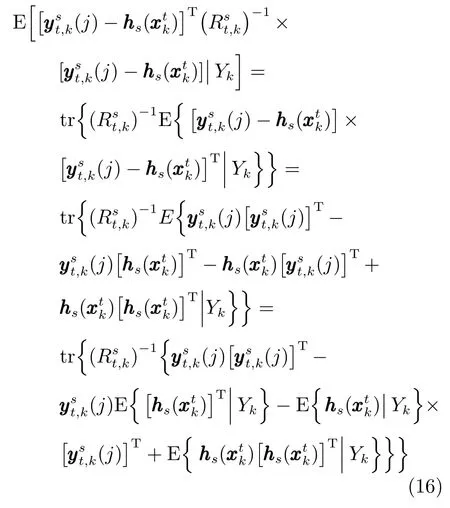
同時可知,k時刻,狀態(tài)向量xtk近似服從

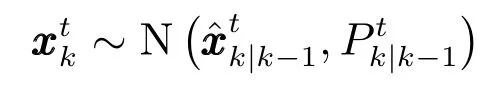
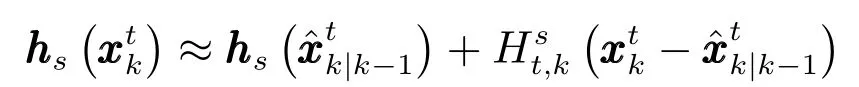
其中

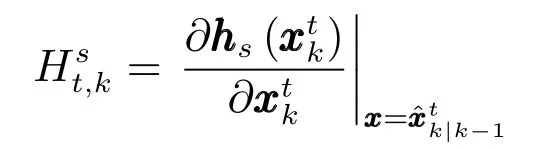
因此,可得

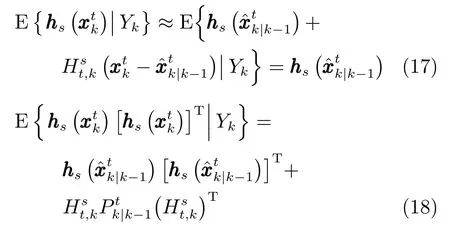
將式(17)和式(18)代入式(16)中,可得

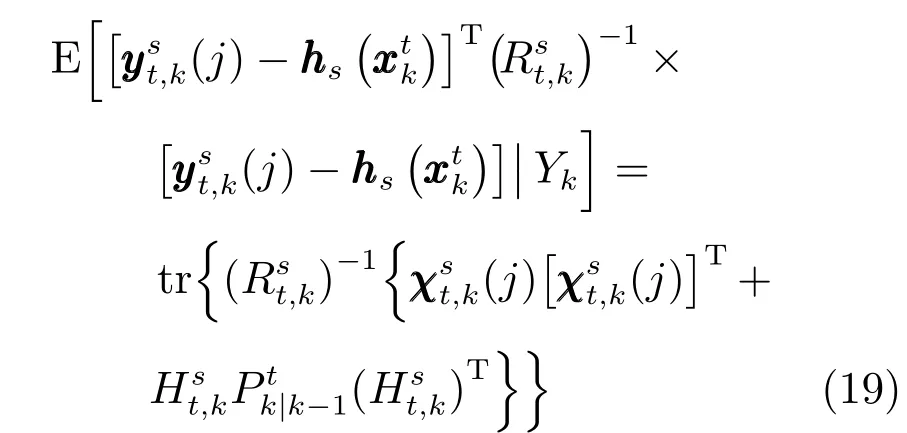
其中,

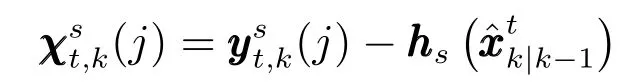
因此,Item2項的條件期望為

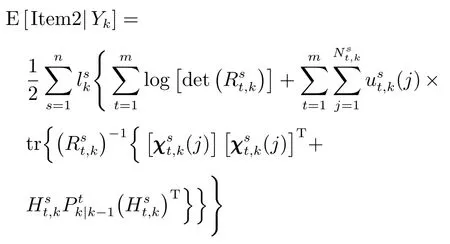
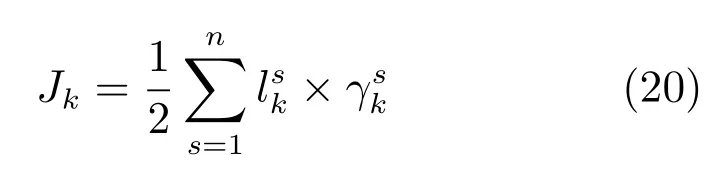
其中,

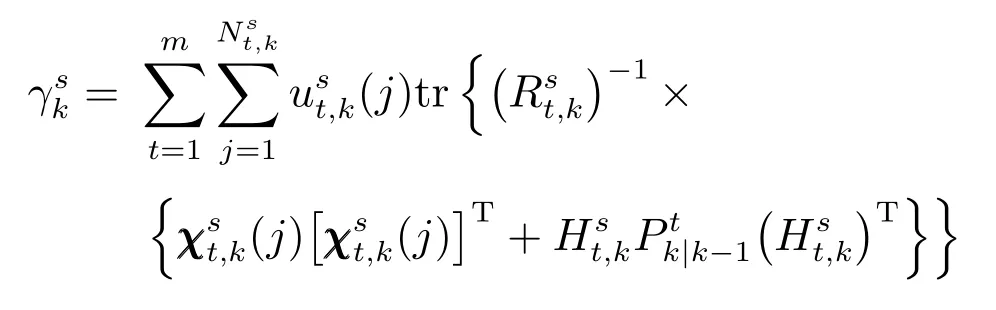
通過極小化傳感器選擇的目標函數(shù)求解傳感器選擇方案Lk,即

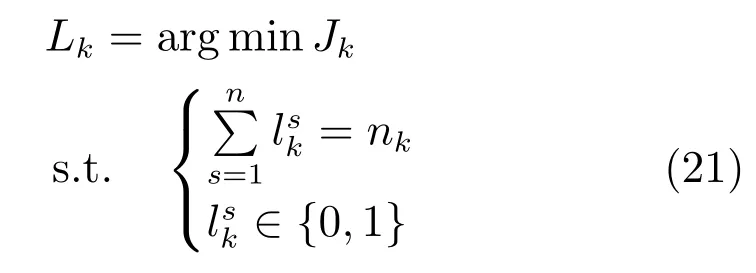
其中,nk為k時刻被選擇的傳感器的數(shù)量,且1≤nk≤n.

目標函數(shù)的解釋:目標函數(shù)中,γks表征傳感器s的所有量測向量與量測一步預(yù)測向量間馬氏距離基于關(guān)聯(lián)向量的加權(quán)(見式(19)).其中,χst,k(j)為量測殘差,當某個傳感器量測值存在由于外界擾動而產(chǎn)生的量測偏差時,由該傳感器量測值求得的會很大,因此本文提出的傳感器選擇算法可以檢測出傳感器是否存在偶然出現(xiàn)的未知系統(tǒng)偏差.通過對所有量測數(shù)據(jù)進行比較,然后進行傳感器選擇,拋棄掉那些會對空間目標產(chǎn)生較大跟蹤誤差的傳感器.

當傳感器可能存在由于環(huán)境的擾動而產(chǎn)生未知系統(tǒng)偏差時,目標函數(shù)可以表征傳感器對空間目標量測的好壞.通過極小化傳感器選擇的目標函數(shù),根據(jù)本文提出的傳感器選擇算法,從所有傳感器中,選擇nk個傳感器進行數(shù)據(jù)融合,得到整個傳感器網(wǎng)絡(luò)對空間目標的跟蹤結(jié)果.

根據(jù)求得的目標函數(shù)(20)以及傳感器選擇的目標(21),本文提出的傳感器選擇算法可以總結(jié)為:

算法1.傳感器選擇算法

輸入.當前k時刻,傳感器網(wǎng)絡(luò)量測值的集合Yks,傳感器選擇數(shù)目nk以及k?1時刻傳感器網(wǎng)絡(luò)對空間目標的估計結(jié)果ρk?1.

輸出.當前k時刻傳感器網(wǎng)絡(luò)的選擇方案Lk.

步驟1.根據(jù)式 (20),求得{γks|s=1,···,n};

步驟2.將求得的按從小到大的順序重新排列,得到;

步驟3.根據(jù)式(21)中傳感器選擇的目標以及nk,從中選擇前nk個傳感器;

步驟4.得到量測k時刻的傳感器選擇方案Lk.

2.3 數(shù)據(jù)融合算法

根據(jù)前面提出的傳感器選擇算法,可以得到k時刻被選擇的傳感器的集合Θk.然后將所選擇的傳感器進行數(shù)據(jù)融合.具體的數(shù)據(jù)融合過程為:

對于選中的傳感器j∈Θk,根據(jù)PDA算法,可以求得該傳感器對空間目標t的估計結(jié)果為,然后將估計結(jié)果傳送到融合中心進行數(shù)據(jù)融合.

為了防止目標t共同的先驗信息對當前k時刻的數(shù)據(jù)融合造成干擾,因此定義k時刻,傳感器j的增量信息矩陣Γtj,k|k和增量信息向量ρtj,k|k分別為

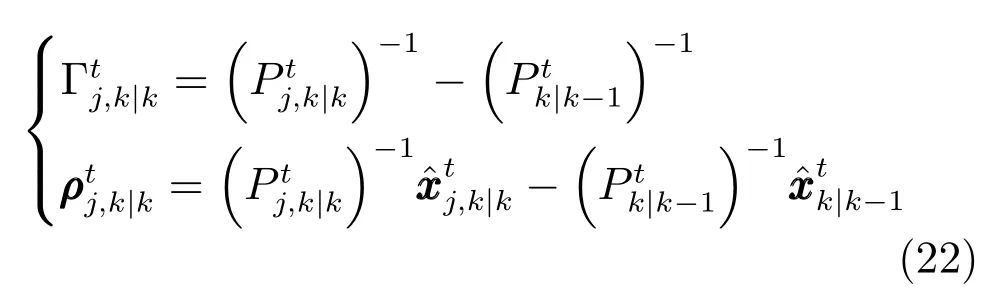
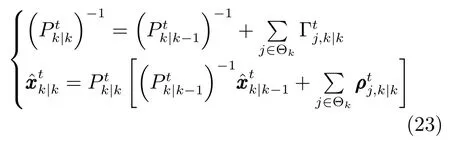
綜上所述,Bayes框架下,基于傳感器選擇的傳感器網(wǎng)絡(luò)目標跟蹤算法可以總結(jié)為:

算法2.基于傳感器選擇的傳感器網(wǎng)絡(luò)目標跟蹤算法

輸入.空間所有目標的狀態(tài)初值和協(xié)方差矩陣初值.

輸出.空間所有目標的估計結(jié)果.

Fork=1,···,N

步驟1.對于傳感器s,求出量測的一步預(yù)測;

步驟2.根據(jù)式(3)求出傳感器s的有效量測集;

步驟3.對于給定的Yts,k,利用數(shù)據(jù)關(guān)聯(lián)算法,求出數(shù)據(jù)關(guān)聯(lián)向量;

步驟4.根據(jù)式(20),求出傳感器選擇的目標函數(shù)Jk;

步驟5.根據(jù)第2.3節(jié)提出的傳感器選擇算法,求出;

步驟6.根據(jù)式(22)和式(23)對選擇的傳感器進行數(shù)據(jù)行融合,求得;

步驟7.Ifk＜N,k=k+1;ElseBreak;

End For

3 數(shù)值仿真

3.1 仿真場景

考慮如下仿真場景:8個離散分布的傳感器同步地對量測空間中的目標進行觀察,傳感器的坐標分別為O1=(0km,0km),O2=(1.5km,1km),O3=(1.2km,1.1km),O4=(2km,2.1km),O5=(1.6km,1.7km),O6=(1.4km,2.1km),O7=(0.42km,1km),O8=(1.2km,1.9km).具體的仿真場景如圖1所示.

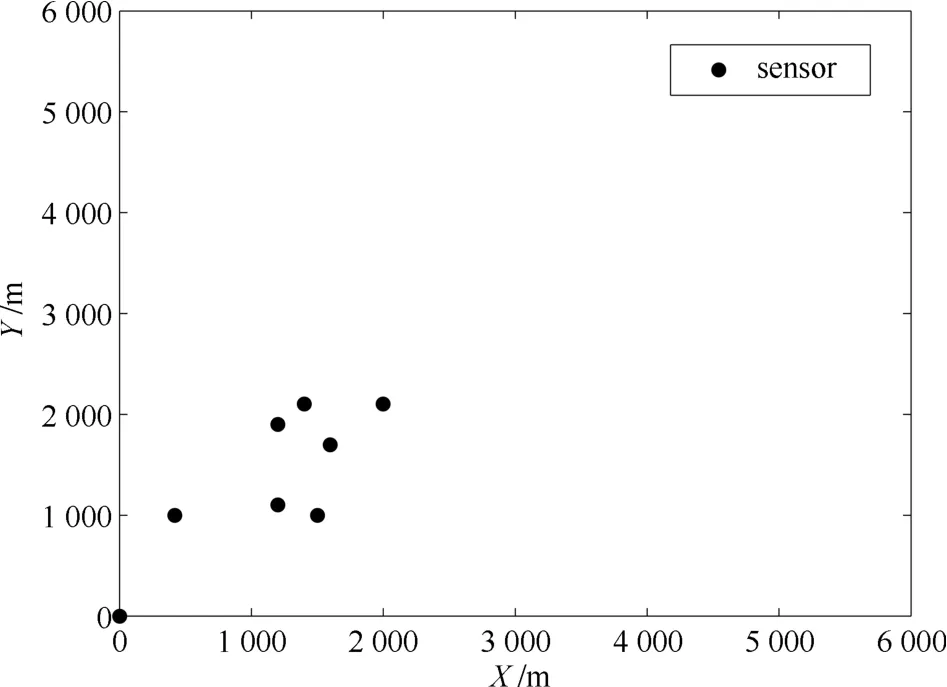
圖1 傳感器網(wǎng)絡(luò)仿真場景Fig.1 Geometry of the sensor network

空間目標的運動模型可以描述為

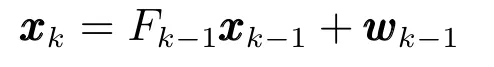
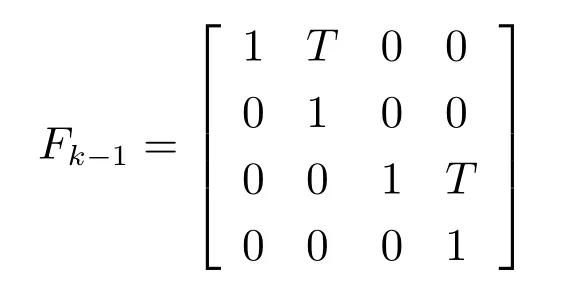
其中,采樣間隔T=1s.

傳感器的量測模型可以表示為

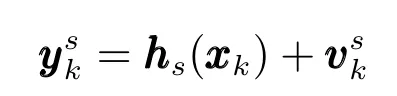
其中,量測噪聲方差矩陣R=diag{(10m)2,(0.1mrad)2},且量測為零均值的高斯白噪聲,量測協(xié)方程滿足

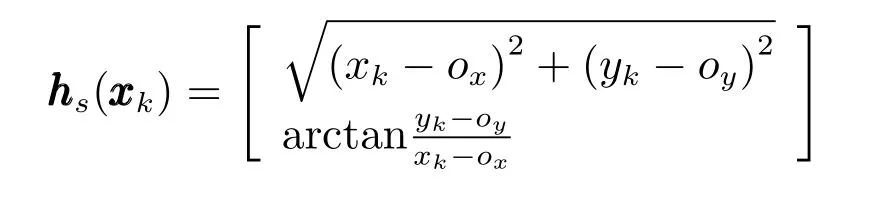
然而傳感器網(wǎng)絡(luò)在量測過程中,不可避免地要受外界環(huán)境的干擾,主要考慮以下幾個方面的量測干擾:1)量測空間中存在少量雜波干擾;2)傳感器可能存在由于外界環(huán)境的擾動而造成的未知系統(tǒng)偏差.因此,本文假設(shè):1)雜波:雜波數(shù)目服從密度為λ=0.05的泊松分布,且雜波在量測空間中均勻分布;2)量測偏差:傳感器2和傳感器4由于外界擾動,存在未知的系統(tǒng)偏差,系統(tǒng)偏差變化情況如圖2所示.

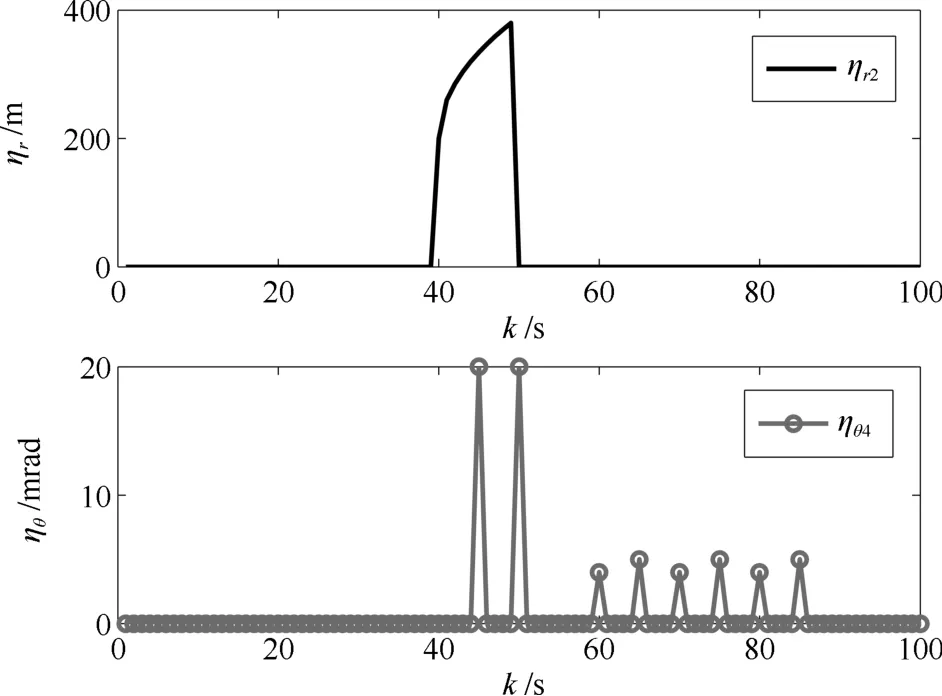
圖2 傳感器系統(tǒng)偏差跳變變化情況Fig.2 Sensors′bias change via sampling time

本文傳感器選擇的目標:從8個傳感器中選擇其中量測效果最好的5個傳感器進行數(shù)據(jù)融合,使得傳感器網(wǎng)絡(luò)對空間目標的跟蹤精度最好.

3.2 單目標跟蹤

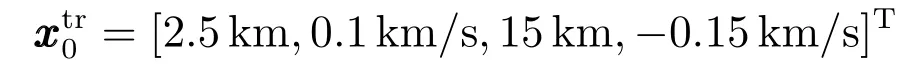
目標狀態(tài)初值為

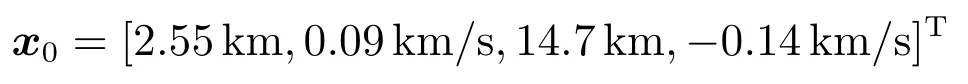
協(xié)方差矩陣的初值為

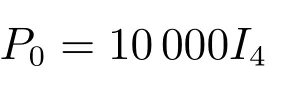
為了證明本文所提算法的有效性,將以下6種算法進行對比仿真:

1)文獻[10]算法:基于最小二乘法的自適應(yīng)野值剔除和加權(quán)融合算法(Least squares);

2)文獻[11]算法:基于多項式外推擬合法的野值剔除和加權(quán)融合算法(Polynomial);

3)文獻[13]算法:基于量測一步預(yù)測向量的野值剔除方法(Residual);

4)文獻[9]算法:試圖對系統(tǒng)偏差進行估計的目標跟蹤算法(Bias registration);

5)本文提出的兩種傳感器選擇算法(Sensor selection);

6)使用全部量測數(shù)據(jù)的傳統(tǒng)目標跟蹤算法(Traditional approach).

空間目標的真實軌跡和傳感器網(wǎng)絡(luò)對空間目標的估計軌跡如圖3所示.基于100次蒙特卡洛

不妨假設(shè)空間目標的真實狀態(tài)初值為(Monte Carlo,MC)仿真,傳感器網(wǎng)絡(luò)對空間目標位置估計的對數(shù)均方根誤差(Root mean square error,RMSE)結(jié)果隨采樣時刻的變化曲線如圖4所示.仿真結(jié)果表明:本文提出的傳感器選擇算法可以準確地對空間目標進行估計,且跟蹤精度優(yōu)于文獻[10]算法、文獻[11]算法、文獻[9]算法和使用全部量測數(shù)據(jù)的傳統(tǒng)目標跟蹤算法.由于上述4種算法對空間目標的跟蹤精度明顯不如本文所提的算法.因此下面重點定量的對照文獻[13]算法和本文算法.

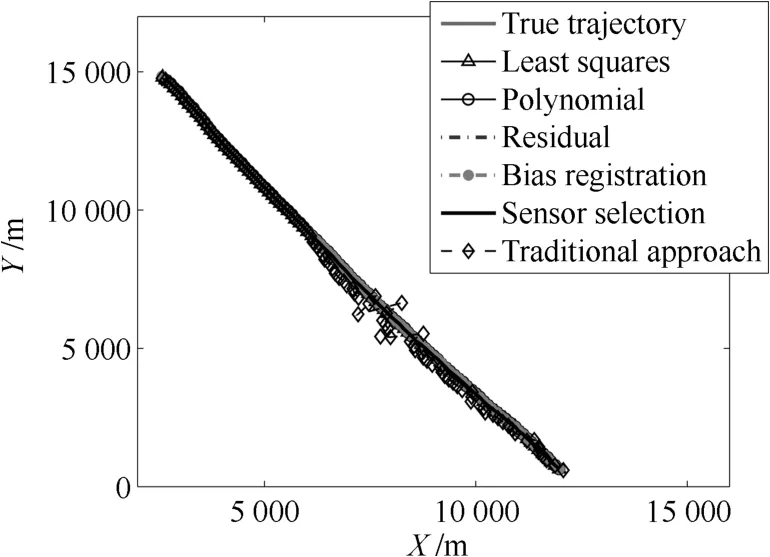
圖3 真實軌跡和估計軌跡Fig.3 True trajectory and the estimated trajectories

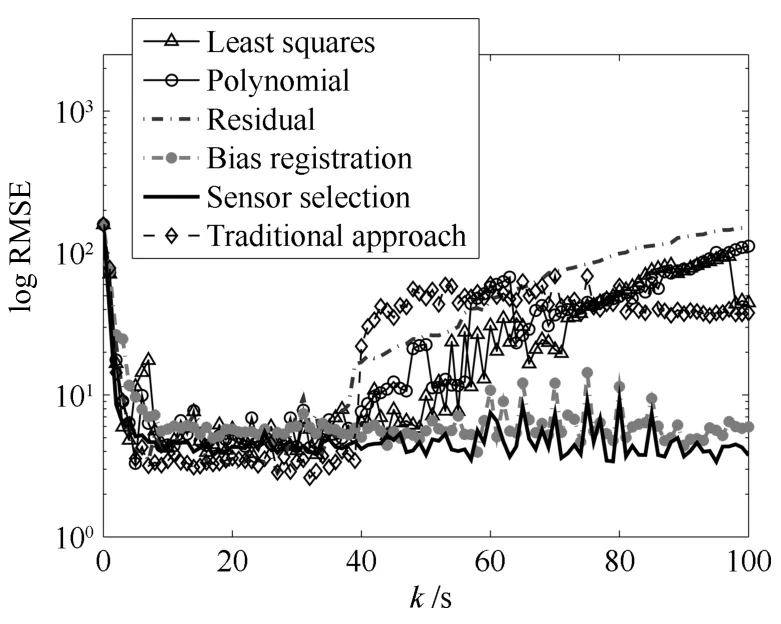
圖4 位置估計RMSE結(jié)果的對數(shù)值隨時間的變化曲線Fig.4 The logic RMSE results on target position via sampling time

基于M=1000次MC仿真,我們首先定義傳感器的選擇概率為

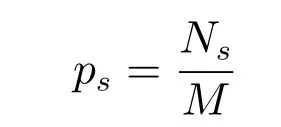
其中,Ns表示1000次MC仿真中,傳感器被選擇的次數(shù).

本文數(shù)值仿真部分,基于1000次MC仿真,近似地用ps表征傳感器的選擇性能.傳感器選擇概率ps隨傳感器未知系統(tǒng)偏差跳變ηr和ηθ的變化情況如圖5所示.假設(shè)所有傳感器在量測過程中的量測噪聲協(xié)方差矩陣都為R=diag{(10m)2,(0.1mrad)2},λ=0.05.

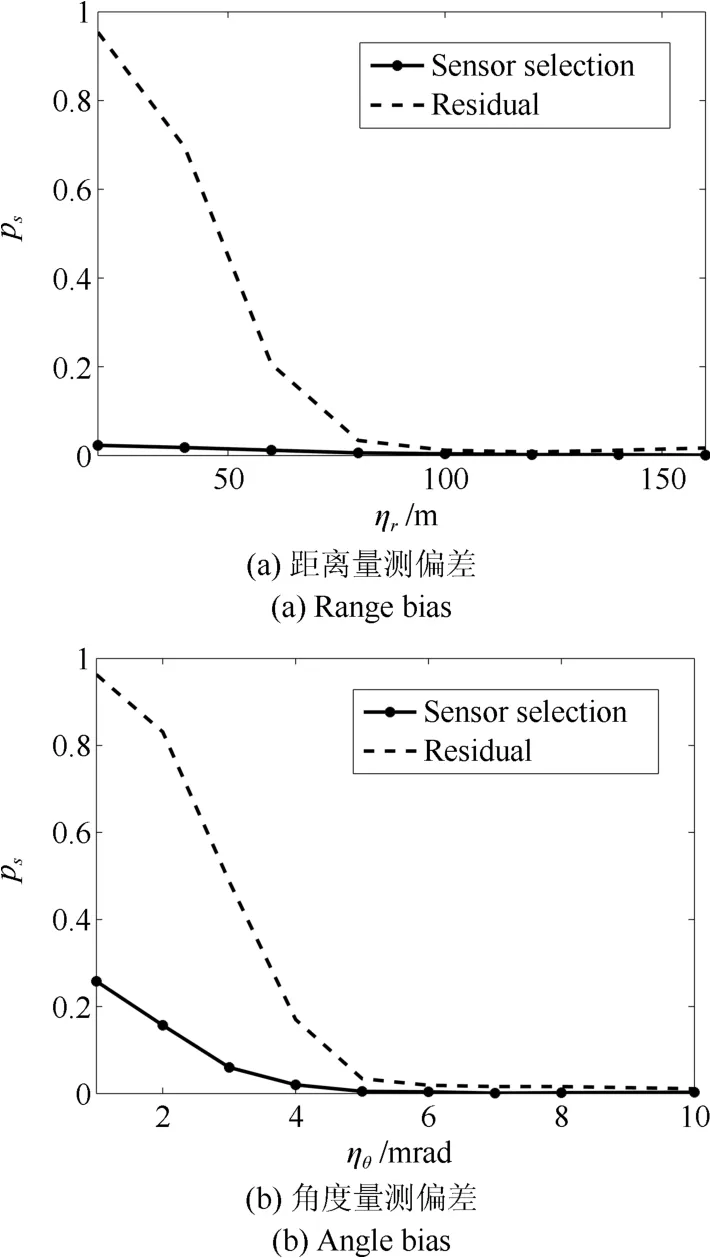
圖5 傳感器選擇概率隨系統(tǒng)偏差的變化情況Fig.5 Sensor selection probability via bias change

數(shù)值仿真結(jié)果表明:當傳感器的距離系統(tǒng)偏差跳變ηr＜80m 或角度系統(tǒng)偏差跳變ηθ＜5mrad時,對照文獻[13]算法對系統(tǒng)偏差跳變的檢測能力明顯不如本文所提算法.因此推斷:當傳感器存在較小的系統(tǒng)偏差跳變時,文獻[13]算法對空間目標的跟蹤性能也會弱于本文所提算法;隨著傳感器系統(tǒng)偏差跳變的增加,兩種算法的傳感器選擇概率ps迅速降低至接近為0.

相應(yīng)地,文獻[13]算法和本文算法對空間目標位置估計的RMSE結(jié)果隨系統(tǒng)偏差跳變量的變化情況如圖6所示.數(shù)值仿真結(jié)果表明:當傳感器系統(tǒng)偏差的跳變量較小時,由于文獻[13]算法對系統(tǒng)偏差跳變的檢測能力較差,而本文算法對較小的系統(tǒng)偏差跳變依舊具有很好的檢測能力,因此本文算法對空間目標位置估計的RMSE結(jié)果遠遠小于文獻[13]算法的RMSE結(jié)果;當傳感器系統(tǒng)偏差的跳變量較大時,兩種算法對系統(tǒng)偏差的檢測能力基本相同,因此兩種算法的RMSE結(jié)果較接近.數(shù)值仿真結(jié)果證明了本文提出的傳感器選擇算法有很好的魯棒性.

算法運行時間也是衡量算法性能好壞的一個關(guān)鍵要素.幾種對照算法的算法復(fù)雜度都相同,都為O(mNsk).所用計算機的硬件配置為Intel(R)Core(TM)i5-4570,3.20GHz;4GB RAM.基于100次蒙特卡洛仿真,運行一次完整的采樣過程k=1s,···,100s,對照算法的算法平均運行時間如表1所示.

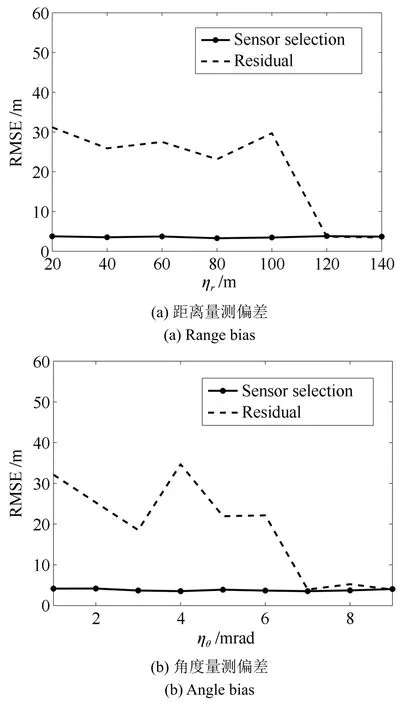
圖6 RMSE隨量測偏差的變化情況Fig.6 RMSE via bias change magnitude

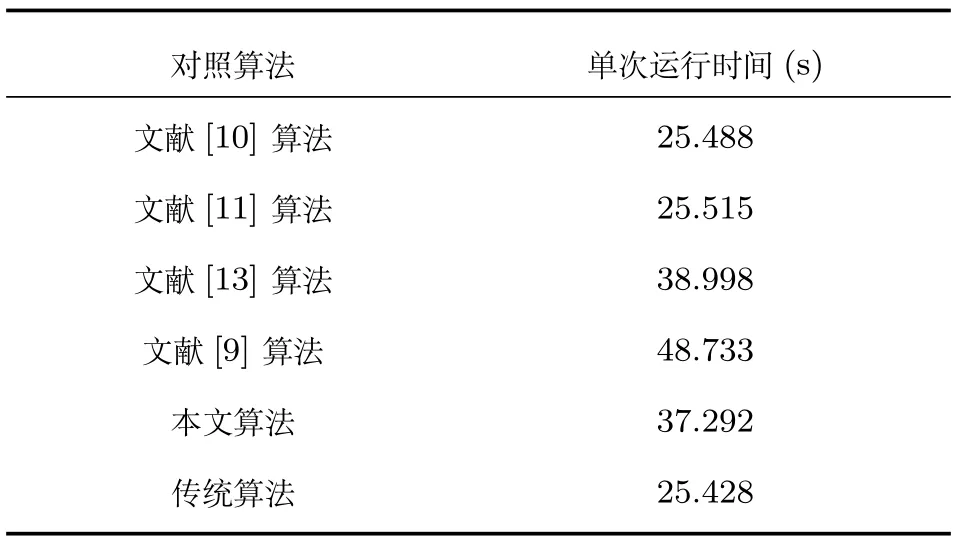
表1 算法單次平均運行時間(基于100次蒙特卡洛仿真)Table 1 One run time of the proposed approaches(100MC runs)

從表1的數(shù)值仿真結(jié)果可以看出,使用全部量測數(shù)據(jù)的傳統(tǒng)目標跟蹤算法由于沒有對量測數(shù)據(jù)進行處理,因此算法運行時間最短,然而該算法的目標跟蹤性能也最差;文獻[9]算法由于需要對系統(tǒng)偏差跳變進行檢測和估計,因此耗時最多;文獻[10]算法和文獻[11]算法使用簡單的野值點剔除算法進行野值點的判斷和剔除,時間消耗相對較低,但是目標跟蹤精度也較差;本文算法借助多傳感器冗余信息處理的思想對傳感器網(wǎng)絡(luò)的量測信息統(tǒng)一進行處理及傳感器選擇,而文獻[13]算法則采用3σ準則對各個傳感器的量測野值點分別獨立的進行判斷,因此本文所提算法的運行時間要略低于文獻[13]算法.

3.3 多目標跟蹤場景

由8個傳感器組成的傳感器網(wǎng)路對量測空間中兩個目標進行觀測,仿真場景如第3.1節(jié)所示.空間目標的真實狀態(tài)初值分別為

傳感器網(wǎng)絡(luò)對空間兩個目標跟蹤的初始狀態(tài)分別為

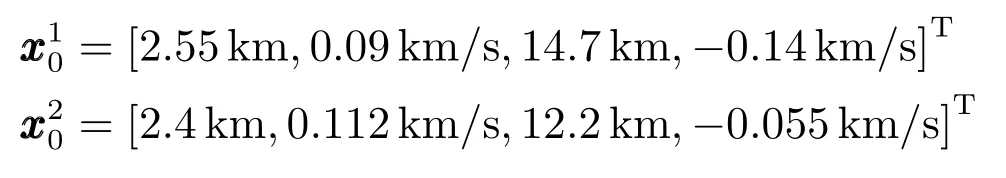
初始的協(xié)方差矩陣都為P0=10000I4.仿真結(jié)果如圖7和圖8所示.

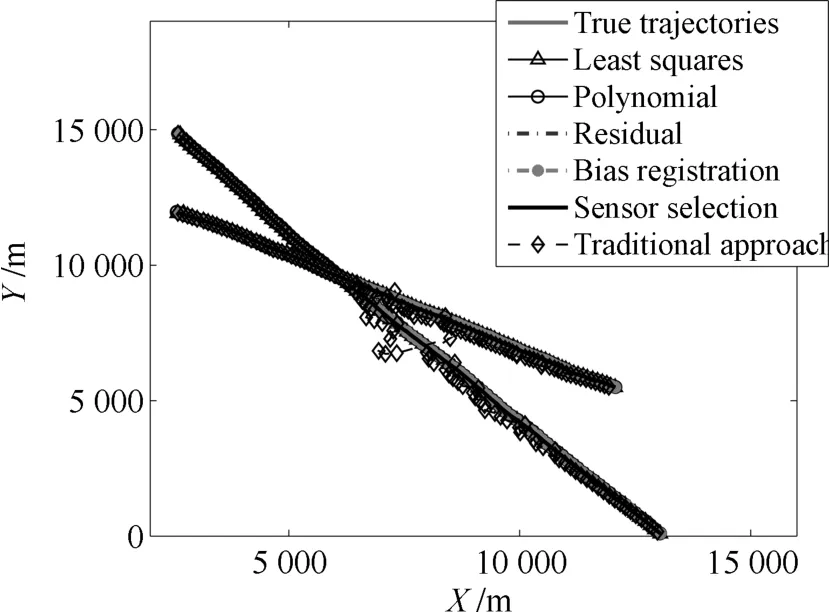
圖7 真實軌跡和估計軌跡Fig.7 True trajectories and the estimated trajectories

空間目標的真實軌跡及傳感器網(wǎng)絡(luò)對空間目標的估計軌跡如圖7所示,傳感器網(wǎng)絡(luò)對空間目標位置估計的對數(shù)RMSE結(jié)果隨采樣時刻的變化情況如圖8所示.數(shù)值仿真結(jié)果表明:本文所提算法可以準確地對空間目標進行跟蹤和估計,且跟蹤結(jié)果明顯優(yōu)于其他幾種對照算法,說明了本文提出的傳感器選擇算法的有效性.

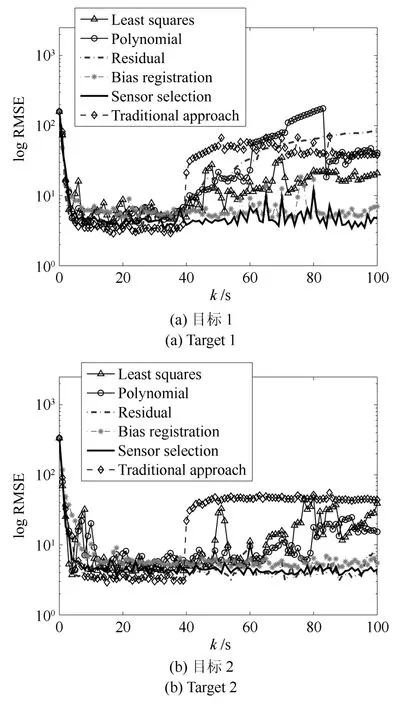
圖8 空間目標狀態(tài)位置估計的RMSE結(jié)果Fig.8 RMSE results on target position estimation

4 結(jié)論

傳感器選擇算法作為一種非常有效的傳感器網(wǎng)絡(luò)目標跟蹤算法,近年來受到了越來越廣泛的應(yīng)用.本文提出了一種全新的基于貝葉斯理論的傳感器選擇算法來解決傳感器網(wǎng)絡(luò)目標跟蹤問題.

本文的創(chuàng)新點可以總結(jié)為:1)本文試圖用傳感器選擇的思路來解決可能帶偶然未知系統(tǒng)偏差(即偏差跳變)的大規(guī)模傳感器網(wǎng)絡(luò)空間目標跟蹤問題;2)本文提出了一種全新的基于貝葉斯框架的傳感器選擇算法來解決傳感器網(wǎng)絡(luò)目標跟蹤問題;3)考慮了實際跟蹤場景中的各種干擾因素,如少量雜波量測的干擾,環(huán)境干擾引起的未知偏差等;4)基于蒙特卡洛仿真討論了不同的量測偏差對傳感器選擇以及目標跟蹤精度的影響;5)對單目標和多目標跟蹤場景分別進行仿真研究,并與傳統(tǒng)的目標跟蹤算法進行對比,證明了所提算法的有效性.

眾所周知,基于隨機有限集理論的方法是處理多傳感器多目標跟蹤問題的一個重要方法,我們將在下一步對基于隨機有限集理論的傳感器選擇問題進行深入研究.