基于橢球擬合的磁力計誤差校正方法研究*

孫 偉,楊一涵,王 野

(遼寧工程技術大學測繪與地理科學學院,遼寧 阜新 123000)

MEMS磁力計工作時不存在累積誤差,在當前狀態沒有干擾磁場的情況下可測量恒定不變的局部磁場矢量,利用該矢量完成載體航向角計算[1-4]。磁力計在實際環境中易受器件自身工藝和結構的限制和周圍磁場的干擾導致測量精度降低,為獲得更精確的磁場信息,就需要對磁力計進行校準[5]。橢圓擬合法局限于二維平面而無法對三維空間中的磁場信息進行校正[6];磁力計受到軟、硬、鐵磁場分別進行補償校正方案存在速度慢效率低的弊端[7]。論文提出的基于橢球擬合校準算法,首先根據磁力計自身誤差和軟硬磁特性建立其誤差模型,通過橢球擬合后利用利用最小二乘平差方法估計出橢球方程系數,從而得到校準后的磁場強度值,實驗結果驗證了算法可行性。

1 磁力計誤差建模

1.1 器件固有誤差建模

制作工藝和結構等引起的磁力計誤差主要包括3個軸靈敏度不一致造成的刻度因子誤差[8]、安裝過程中出現的3個軸非正交誤差和零偏誤差[9]。

建立誤差模型:

Hm=KPHb+Bd

(1)

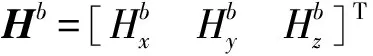
1.2 環境擾動建模

外部環境干擾主要包括硬鐵干擾和軟鐵干擾[10]。硬鐵干擾在載體上的永久磁鐵或磁化介質等硬磁材料上產生,在沒有外界磁場作用時不產生磁性,而當這種材料受到外界磁場作用會發生磁化,其自身產生一個不受外界磁場影響、不隨時間位置變化的固定磁場,其磁場強度和方向保持不變,由于硬磁材料和傳感器都固定在載體上,所以不會隨載體姿態變化而變化。由硬鐵干擾產生的磁場會導致磁力計輸出產生偏差,因此硬鐵模型是磁力計各軸輸出值與一個偏置矢量R相加的和,為一固定常值;軟鐵干擾主要由地磁與軟磁材料之間的相互作用引起,與硬磁材料不同的是,軟磁材料被周圍環境磁場磁化后產生的磁場的磁場強度與方向和外界磁場有關,會隨著外界磁場的磁場強度大小和方向的變化而變化因此軟鐵模型是磁力計各軸輸出值前乘以一個系數矩陣L。得到考慮環境因素建立的磁力計誤差模型為:

(2)

結合式(1)和式(2),得到磁力計誤差模型:

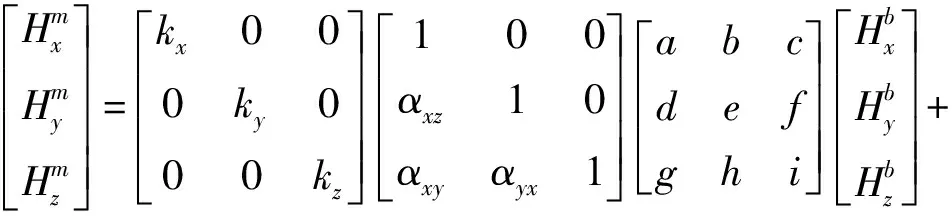
(3)

即:

Hm=DHb+B

(4)

式中:矩陣D為3個系數矩陣的乘積;矩陣B為零位偏差Bd和硬磁誤差Bh的和。磁力計中存在的傳感器噪聲對輸出值的影響可忽略不計,因此在模型中給予忽略。對式(4)進行轉換,可將磁力計存在誤差干擾的輸出值校準為實際磁場中真實值:

Hb=D-1(Hm-B)=E(Hm-B)

(5)

式中:E為矩陣D的逆矩陣。

2 橢球擬合校準算法

2.1 橢球擬合原理

在環境不變的情況下,傳感器每個姿態感受的磁場強度是相同的。在沒有偏差和傳感器內部x,y,z軸相互垂直的情況下,磁力計測量的x,y,z軸的值可在三維空間中組成一個球面。但是在實際工作環境中的磁力計受刻度因子、三軸非正交和零偏等誤差及外界環境中硬、軟鐵等誤差影響,使得3個敏感軸輸出數據構成一個球心偏離坐標系原點的橢球[10-11]。因此磁通量在三維空間組成的橢球球心坐標是磁力計校準的一部分。

二次曲面方程的一般形式:

(6)

寫成矩陣形式后簡化:

(7)

2.2 橢球擬合算法

利用橢球擬合方法進行磁力計誤差校正的實質就是通過橢球擬合算法算出球心坐標和橢球方程系數,將球心擬合到坐標系原點,并且通過求得的系數得到校準矩陣和偏移矢量,以得出磁場強度的真實值從而達到校正誤差的目的。

由磁力計綜合誤差模型構成橢球方程:

(Hb)T(Hb)=[E(Hm-B)]T[E(Hm-B)]
=(Hm)TC(Hm)-2BTACHm+BTCB

(8)

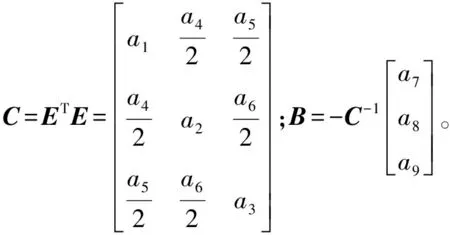
由磁力計測量值數據得出線性方程組:

(9)

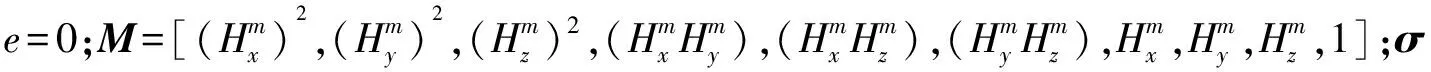
最后要使殘差e最小,以磁力計采集的原始數據與橢球面的距離平方和最小為判斷準則,應用最小二乘估計法得出橢球方程各個系數,

(10)

因此,可求得校準矩陣E和偏移矢量B。

3 實驗結果及分析

采用實驗室現有的MTi-G-710型MEMS慣性測量單元內置磁傳感器搭建測試環境,技術指標如表1所示[12-13]。

表1 Mti-G-710內置磁力計性能指標

為驗證橢球擬合算法可行性,在傳感器周圍固定一個鐵塊模擬工作環境下的磁干擾,實驗環境如圖1所示。

圖1 實驗環境

將傳感器在三維空間中任意旋轉5 min,使采集的數據盡可能覆蓋整個橢球面,基于本文提出的算法利用MATLAB軟件處理原始數據,應用最小二乘法可求出擬合的橢球方程各系數為:

σ=[1.140 4,1.080 6,1.113 0,-0.014 6,-0.009 3,

0.018 6,-0.001 2,0.028 3,-0.262 8]

得到校準矩陣E和偏移矢量B:

將校準矩陣E和偏移矢量B代入式(8)即可得到校正后的磁力計輸出。

根據圖2所示對比修正前后磁場強度曲線,解算出表2所示的兩球球心坐標。可看出原始數據在坐標系中形成的軌跡原點由于自身誤差和周圍磁場干擾導致其偏離坐標原點,經過橢球擬合誤差校正之后的磁場強度數據擬合的球體球心更接近坐標系原點。

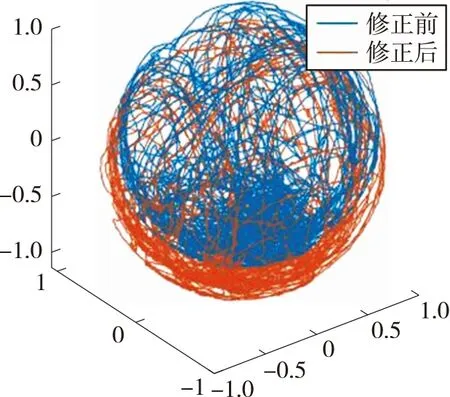
圖2 校正前后磁場強度對比曲線

xyz校正前0.002 60.030 20.236 7校正后0.000 20.000 70.010 0

將磁力計輸出的原始磁場強度模值與校正后的磁場強度模值進行對比(如圖3)后發現:校正后的磁場強度模值波動小于原始磁場強度模值,校正后的磁場強度標準差為0.0519遠小于校正前磁場強度標準差0.146 2。

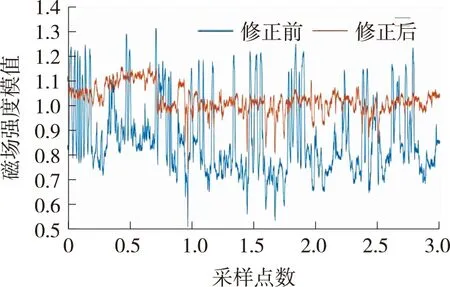
圖3 磁場強度模值比較曲線

4 結論

論文提出一種磁力計橢球擬合誤差校正算法,基于誤差模型建立橢球擬合校正模型,利用最小二乘法解算出校準矩陣和偏移矢量得到校準后磁場值。實驗結果表明橢球擬合算法可有效降低器件自身誤差及外界硬、軟鐵干擾等引起的器件輸出誤差,實現對三維磁力計的有效校正,可進一步提高載體運動信息獲取的準確性和實時性。