帶有Elastic Net懲罰的貝葉斯分位數回歸及其數值模擬

劉亞新

（中南大學 數學與統計學院，長沙 410083）

0 引言

自1978年Koenker和Bassett[1]提出分位數回歸的概念以來，分位數回歸因能提供更全面的信息以及優良的性質，在理論和應用領域都得到了廣泛的研究和應用。Yu和Moyeed[2]最早提出了貝葉斯分位數回歸，將分位數回歸問題與非對稱拉普拉斯分布（Asymmetric Laplace Distribution,ALD）聯系起來，分位數回歸系數估計的最小化問題等價于誤差項服從非對稱拉普拉斯分布的似然函數的最大化問題，進而采用貝葉斯方法估計分位數回歸的系數，該方法在計量經濟學領域受到了越來越多的關注。由于似然函數很復雜，參數的后驗分布不是熟悉的函數形式，因此常常用MCMC方法對參數的后驗分布進行抽樣模擬，得到參數的貝葉斯估計。Yu和Moyeed采用的是隨機游走M-H算法，建議分布為以當前參數值為均值的正態分布。盡管該方法非常方便地產生候選值，但是接受率依賴于分位數，而且收斂速度很慢。Kozumi和Koboyashi[3]提出了基于非對稱拉普拉斯分布的位移-尺度模型的Gibbs抽樣算法。該算法根據參數的全條件后驗分布進行抽樣，而全條件后驗分布是已知的函數形式，這大大提高了抽樣的收斂速度，因此得到了廣泛應用。

對分位數回歸中的變量選擇問題，Koenker[4]首次將Lasso的思想應用于分位數回歸中。Wang等[5]將最小絕對差估計與自適應Lasso懲罰結合起來進行變量選擇。Li和Zhu[6]將Lasso的思想應用于分位數回歸中進行變量選擇，將系數的絕對值和作為懲罰部分，提出了計算Lasso分位數回歸的全部正則化路徑的有效算法，同時又對擬合模型的有效維數進行估計，可以用來選擇正則化參數。Wu和Liu[7]證明了SCAD方法和自適應Lasso分位數回歸的Oracle性質。Park和Casella[8]從貝葉斯角度研究Lasso分位數回歸問題，提出了分層模型，并用Gibbs抽樣進行參數估計。Li等[9]從貝葉斯的角度研究Lasso分位數回歸，提出了一個分層模型的框架，將參數的先驗分布設成拉普拉斯先驗，并用Gibbs算法進行抽樣，實驗證明貝葉斯Lasso分位數回歸比其他方法的Lasso分位數回歸更優。Alhamzawi等[10]提出了貝葉斯自適應Lasso分位數回歸，對不同的回歸系數賦予不同的懲罰參數，且懲罰參數的先驗設為倒伽瑪分布，并把倒伽瑪分布的超參數設成未知量，采用Gibbs算法對后驗分布抽樣來估計參數。

本文對帶有Elastic Net懲罰的貝葉斯分位數回歸提出了更簡單的估計方法，使所有參數的全條件后驗分布都是熟知的分布形式，可以采用Gibbs算法進行抽樣，避免了Gibbs抽樣中又包含M-H抽樣的問題[9]，提高了迭代效率。

1 帶有Elastic Net懲罰的貝葉斯分位數回歸

1.1 分位數回歸

給定訓練數據{(xi,yi),i...,n},xi為預測變量，yi為響應變量，預測變量xi與響應變量yi滿足：

其中β=(β1，β2，...，βk)T∈Rk,εi是誤差項，且相互獨立，滿足εi的第τ分位數為0，即的τ分位數回歸方程可以寫為：

根據Koenker和Bassett[1]的理論，分位數回歸系數β的求解可轉化為下列優化問題：

其中ρτ(u)=u(τ-I(u＜0))是損失函數，I(·)表示示性函數。

Yu和Moyeed[2]指出，在假設誤差服從非對稱拉普拉斯分布的前提下，最小化問題（3）可以轉化為最大化似然函數問題。即假設誤差項εi服從非對稱拉普拉斯分布ALD(0，σ，τ)，其中σ是尺度參數，εi的密度函數為：

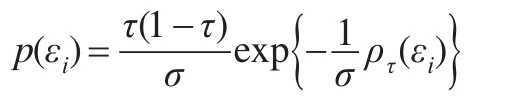
可以證明，服從該分布的變量的τ分位數是0。進而yi|xi，β，σ~ALD(，σ，τ)，密度函數為：

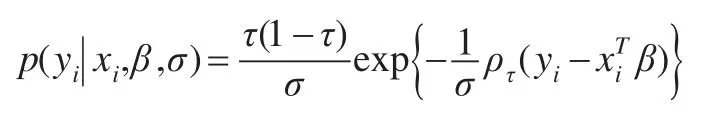
樣本集y=(y1，y2，...，yn)T的似然函數為：

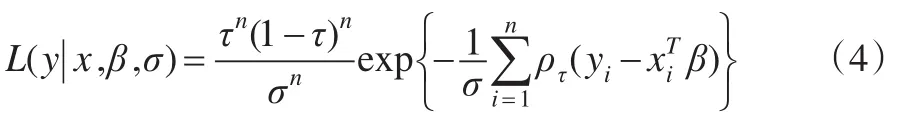
需要說明的是，誤差ε并不是真的服從ALD分布，這樣的假設只是為了將最小化問題（3）轉化為最大化似然函數（4）。不管數據的原始分布是什么，使用非對稱拉普拉斯分布都是一種有效的擬合貝葉斯分位數回歸的方式，即使誤差不是真的服從非對稱拉普拉斯分布，參數估計仍能取得很好的效果。

1.2 基于Elastic Net懲罰的貝葉斯分層模型

帶有Elastic Net懲罰的分位數回歸的參數估計模型為：

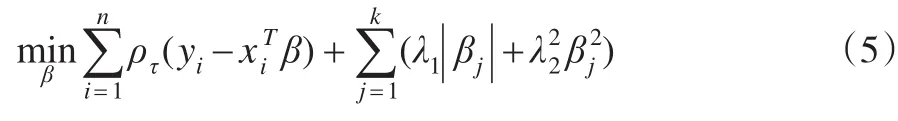
由于：

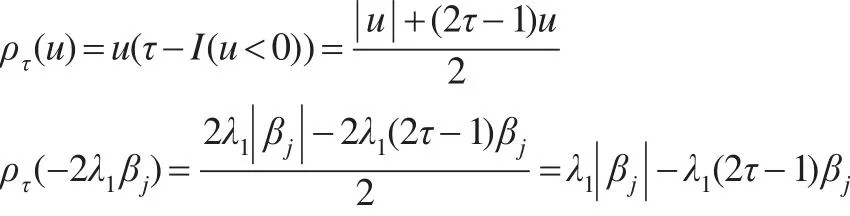
式（5）可以轉化為:

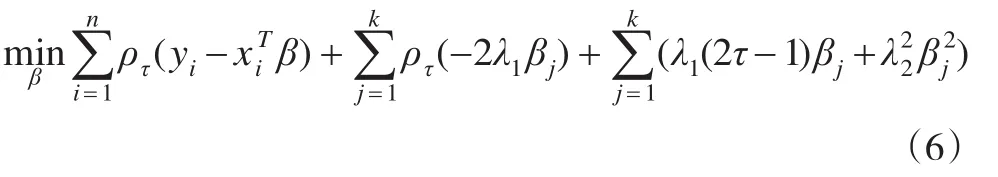
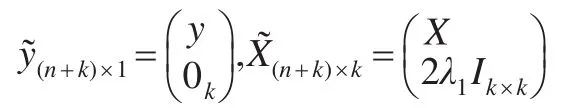
其中X=(x1，x2，…，xn)T，Ik×k表示k階單位矩陣，則式（6）將變為:

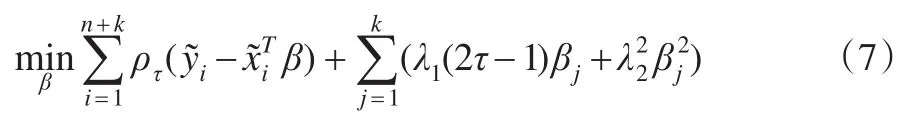
令:

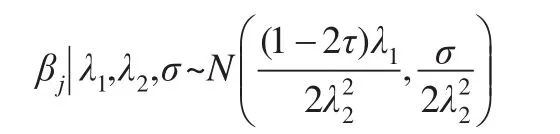
則:

可以看出，最小化式（7）相當于最大化式（8）。令η=，為了得到各參數的全條件后驗分布，將非對稱拉普拉斯分布用指數分布和正態分布混合表示。Kozumi和Kobayashi[11]已證明，若z服從指數分布exp(τ(1-τ)σ)，v服從標準正態分布N(0,1)，誤差項可以表示為:

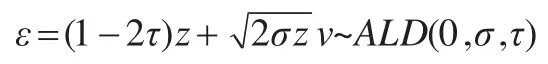
從而:yi|xi，zi，β，σ~N(+(1-2τ)zi，2σzi)

為了得到參數的貝葉斯估計，需要指定各參數的先驗分布。本文對尺度參數σ，懲罰參數(λ1，η)分別采用各自的共軛先驗分布，σ的先驗分布為倒伽瑪分布IG(a，b)，λ1的先驗分布為N(μ，δ2)I(λ1＞0)，η的先驗分布為廣義倒高斯分布GIG(c，d，f)，其概率密度函數為:

則式（1）將轉化為:

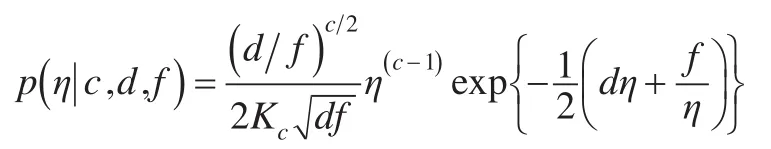
其中Kc是第二類修正貝塞爾函數，d＞0，f＞0，c是實數。

外墻保溫性能的高低，將會直接影響舊工業建筑改造后日常運營中的能耗，利用原有厚磚墻的畜熱性能在此基礎上采取修復、增加保溫層等措施進行外墻的改造設計。一般情況下，舊工業建筑的外窗氣密性和保溫性能差，應進行節能計算采取相應的改造更換措施，將原單層平板玻璃更換位為中空低輻射節能玻璃。屋頂保溫性能設計。采取更新原來保溫層的辦法進行改造設計。

綜上所述，得到如下的貝葉斯分層模型：

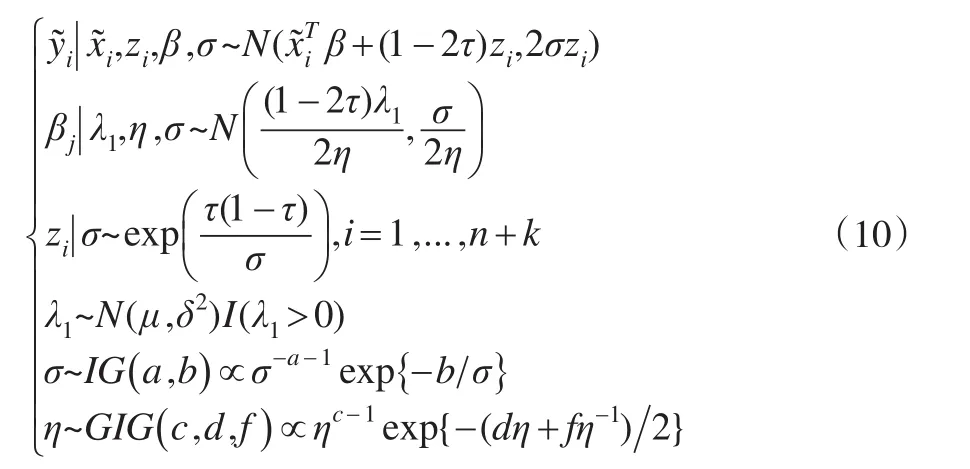
1.3 Gibbs抽樣

由貝葉斯分層模型可得，參數 (β，σ，λ1，η，z)的聯合后驗密度為：

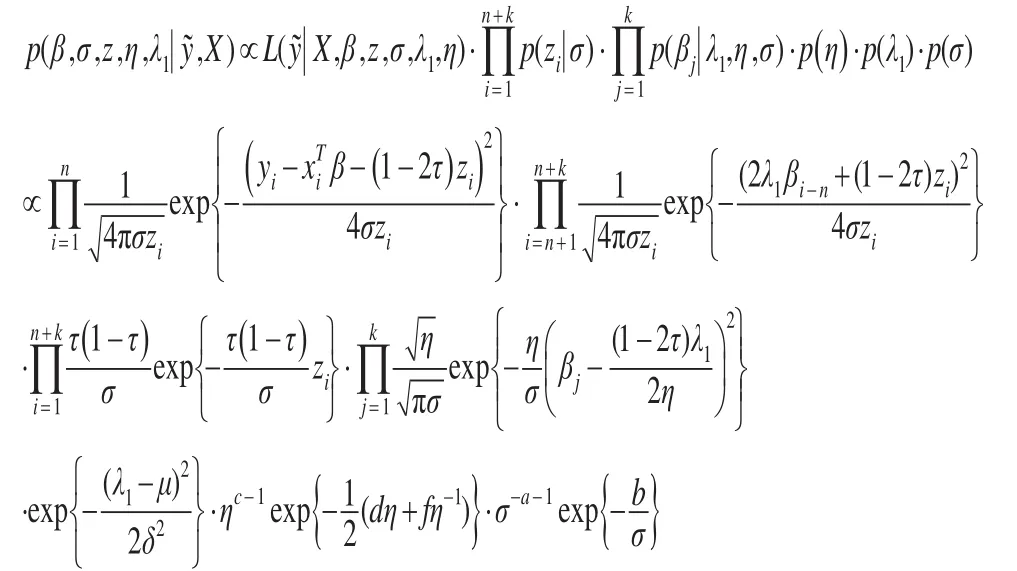
根據貝葉斯定理，回歸系數βj的全條件后驗密度為：

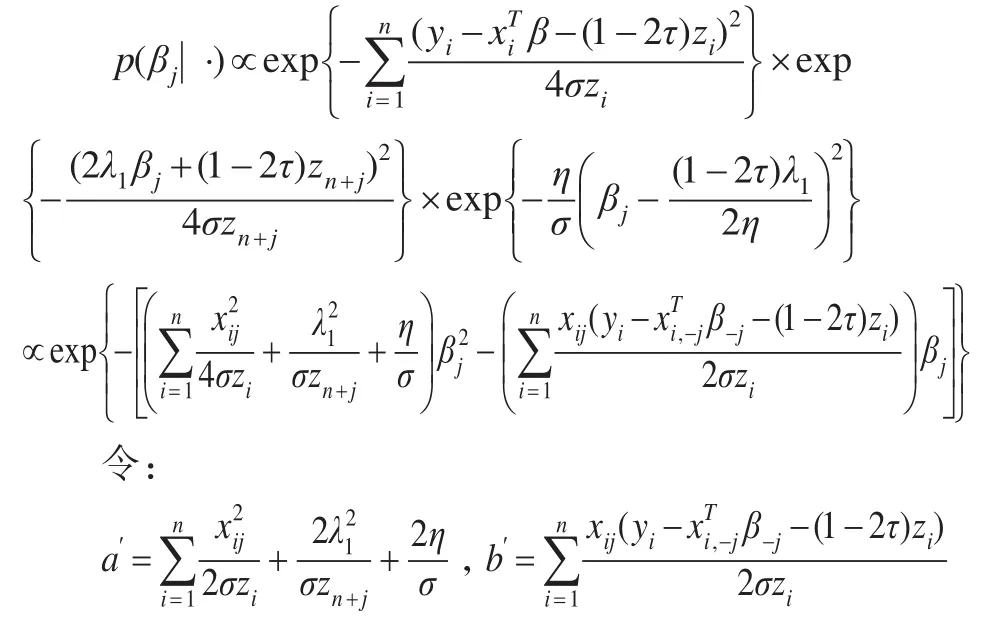
其中β-j表示去除參數βj之后的參數向量，xi，-j也類似，則βj的全條件后驗分布為正態分布N(ba′，1a′)。

參數σ的全條件后驗密度為：

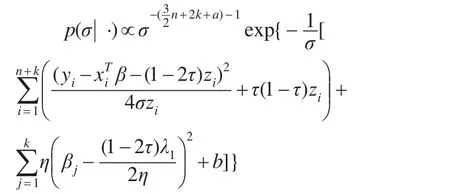
故參數σ的全條件后驗分布為倒伽瑪分布，即：

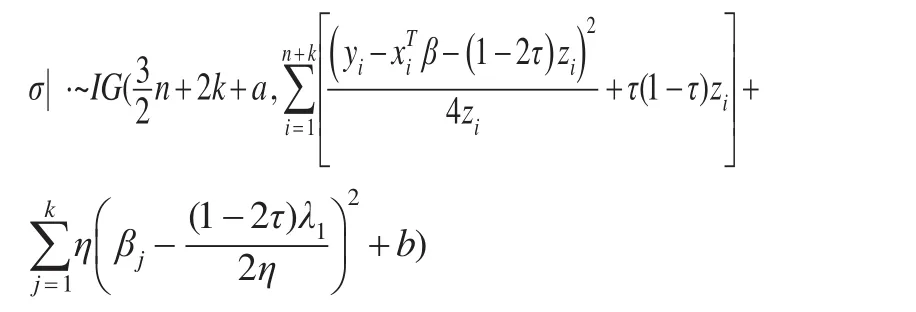
同理可得其他參數的全條件后驗分布分別為：

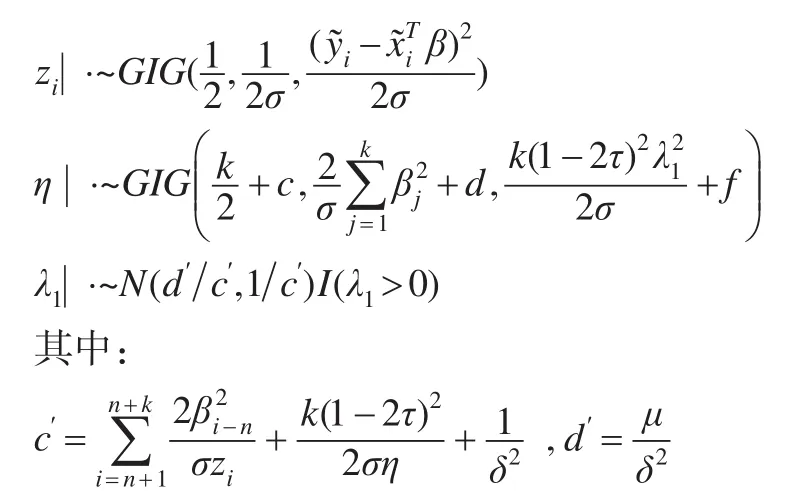
由各參數的全條件后驗分布可以采用Gibbs算法進行抽樣，其中廣義倒高斯分布的抽樣可以參考Dagpunar[12]和J?rgensen[13]，也可以借助 R軟件中GeneralizedHyperbolic程序包中的rgig函數。

2 數值模擬

2.1 獨立同分布情形

對于獨立同分布情形，本文采用在這一研究領域經常使用的數值模擬模型：

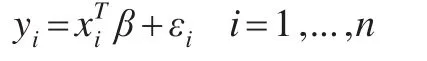
其中回歸系數分為以下兩種形式：

Case1：β=(3，1.5，0，0，2，0，0，0)T

Case2：β=(0.8，0.8，0.8，0.8，0.8，0.8，0.8，0.8)T

Case1和Case2分別對應稀疏和密集的情形。在Case1中，自變量的樣本數據產生于多元正態分布Nk( )0，Σx，誤差ε~N(0，1)。在Case2中，自變量的樣本數據產生于多元正態分布誤差ε~N(0，1)。模型生成20組數據集，每組數據集中有400條訓練樣本，100條測試樣本。評價指標為對測試樣本計算的均值絕對差的均值（MMAD）和標準差（SD），即：

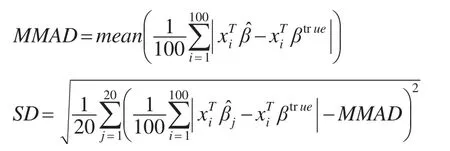
分別估計分位數τ=(0.3，0.5，0.8)時的分位數回歸模型。

表1和表2（見下頁）分別是獨立同分布情形下Case1的參數估計結果和MMAD（SD）值。可以看出，在參數估計方面，帶Elastic Net懲罰的分位數回歸方法比QRLasso方法和QR-SCAD方法更準確，但是其MMAD值和SD值比這兩種方法都大，而只比QR方法小，說明當預測變量之間的相關性較低時，帶Elastic Net懲罰的分位數回歸方法的優勢并不十分明顯。

表1 獨立同分布情形下Case1的參數估計

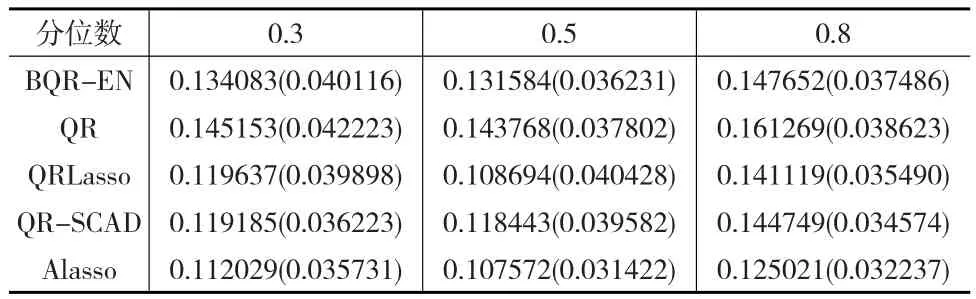
表2 Case1各方法的MMAD(SD)值

表3和表4分別是獨立同分布情形下Case2的參數估計結果和MMAD（SD）值。Case2對應密集的情形，并且變量之間存在較高的相關性，可以看出帶Elastic Net懲罰的分位數回歸方法凸顯出了優勢，其MMAD(SD)值比其他四種方法都要小，而且參數估計也相對更加準確。這說明帶Elastic Net懲罰的分位數回歸方法在變量之間存在比較嚴重的多重共線性時具有明顯的效果，同時也具有較強的穩健性。

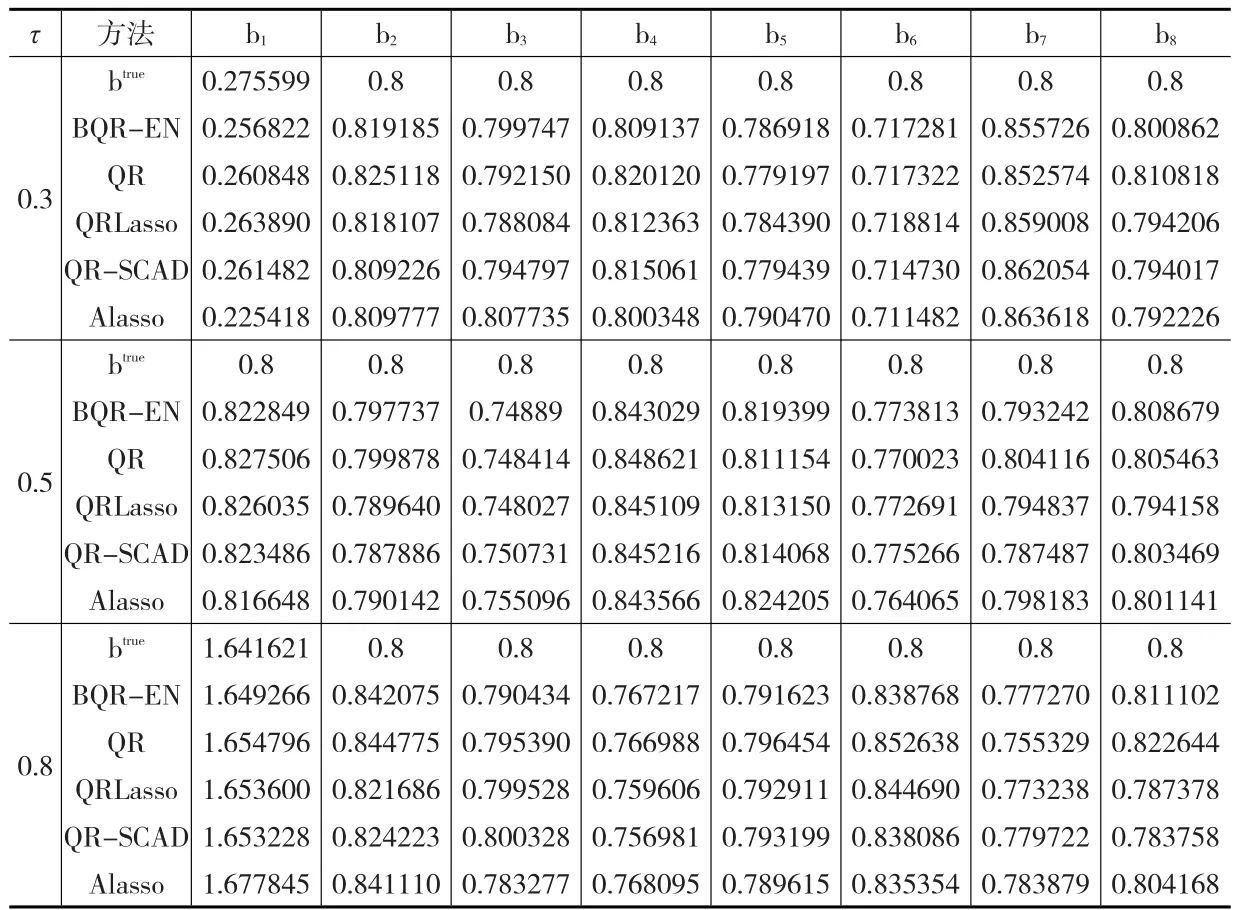
表3 獨立同分布情形下Case2的參數估計

2.2 非獨立同分布情形

對于非獨立同分布下的數值模擬，本文采用如下回歸模型：

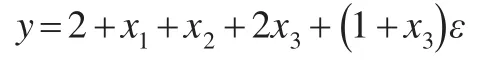
預測變量x1，x2，…，x7的樣本數據產生于均勻分布U(0 ，1) ，誤差項ε~N(0 ，1)。與獨立同分布情形類似，模型生成20個數據集，每個數據集中有400條訓練樣本，100條測試樣本，估計分位數τ=0.2，0.3，0.5下的分位數回歸方程。

表5和表6（見下頁）分別是非獨立同分布下的參數估計結果和MMAD（SD）值。可以看出，在非獨立同分布下，五種方法仍能得到比較準確的估計。其中，本文的方法在預測方面具有較小的標準差(SD)，總體上要優于QR方法和QRLasso方法。Alasso方法雖然比帶Elastic Net懲罰的分位數回歸方法有更小的MMAD值和SD值，但是其不能解決預測變量個數大于樣本量這種情況，而且Alasso方法的懲罰參數多，抽樣復雜，沒有帶Elastic Net懲罰的分位數回歸方法便于理解，易于操作。

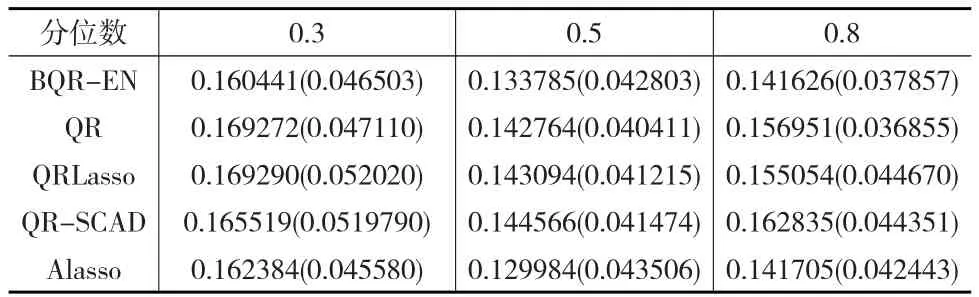
表4 Case2各方法的MMAD(SD)值

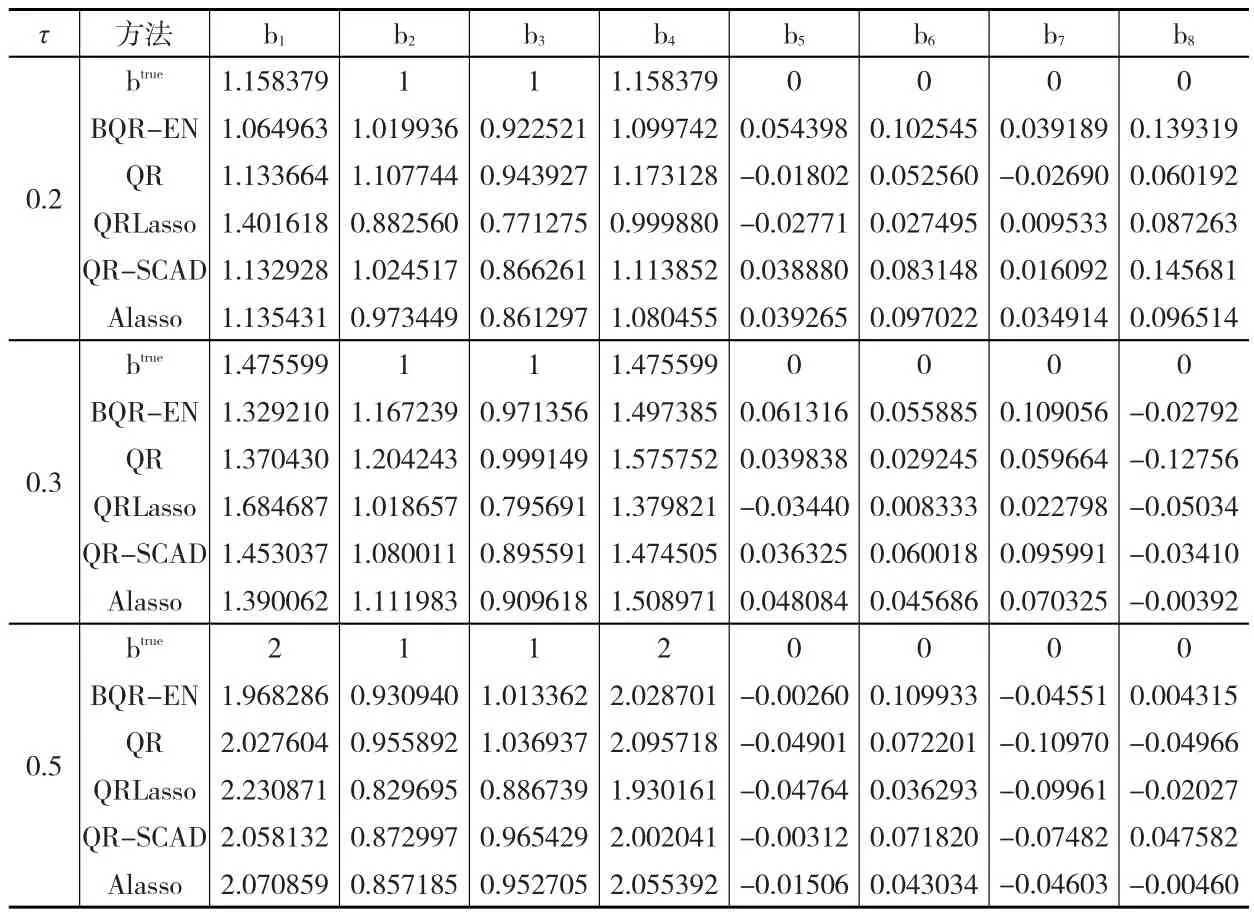
表5 非獨立同分布情形下的參數估計

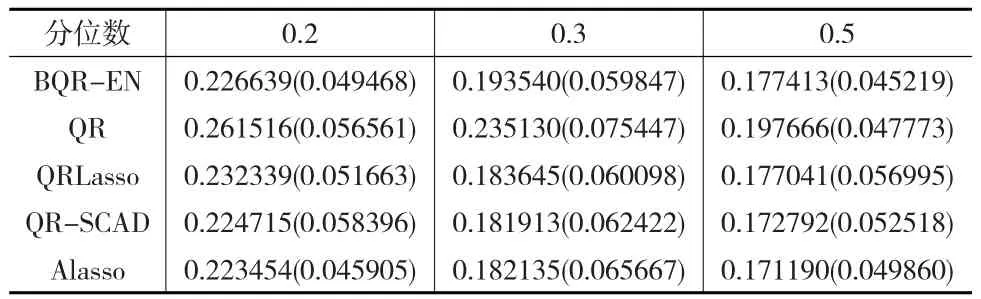
表6 非獨立同分布情形下各方法的MMAD(SD)值

3 結論

帶有Elastic Net懲罰的參數估計方法是對Lasso方法的改進，可以解決預測變量大于樣本量情況下的變量選擇問題，并且當預測變量間存在著較高相關性時，Elastic Net懲罰仍然能得到比較準確的參數估計。本文研究了帶有Elastic Net懲罰的貝葉斯分位數回歸問題，建立了相應的貝葉斯分層模型，使Gibbs抽樣成為可能，提高了馬爾科夫鏈的收斂速度，同時在參數估計和預測方面也具有較小的偏差。