基于站點(diǎn)及共線運(yùn)行的公交乘客路徑選擇模型

徐海軍，趙 靖 （上海理工大學(xué) 管理學(xué)院，上海 200093）

XU Haijun,ZHAO Jing (Management School,University of Shanghai for Science and Technology,Shanghai 200093,China)

0 引言

公共汽車交通出行是一種綠色高效的出行方式[1-2]，但由于城市公交線路走向和站點(diǎn)分布的復(fù)雜性，如何尋找最為便捷快速的公交出行方案，成為城市居民和外地旅客在使用公交出行中最為關(guān)注的問(wèn)題[3]。因此，有必要采取合適的方法為公交乘客選擇合理的乘車線路和換乘站點(diǎn)，以提高公交出行效率。

由于公交系統(tǒng)由站點(diǎn)和線路構(gòu)成，在運(yùn)營(yíng)中存在共線運(yùn)行，使得公交出行路徑選擇與小汽車交通相比，有其顯著的特點(diǎn)。主要體現(xiàn)在出行者并不在意具體的行駛路徑，甚至不拘泥于乘坐的線路，相比小汽車交通無(wú)法同時(shí)嘗試兩條不同的線路，在公交共線運(yùn)行區(qū)段，公交出行者可在換乘站選擇多條均可到達(dá)目的地的線路中最先到達(dá)的公交線路。

本研究將針對(duì)公交系統(tǒng)的這一特征，考慮站點(diǎn)及共線運(yùn)行，建立公交出行路徑選擇模型。

1 相關(guān)研究綜述

關(guān)于公交乘客出行路徑選擇的方法主要有以下三類：（1）基于傳統(tǒng)小汽車交通出行最短路徑算法。這類算法是研究路網(wǎng)中兩點(diǎn)間阻抗最小的路徑，針對(duì)小汽車交通，有包括Di jkstra算法、Floyd-Warshall算法等經(jīng)典算法[4]。在此基礎(chǔ)上，后續(xù)研究從駕駛員偏好、多任務(wù)點(diǎn)以及緊急救援等方面，提出了一系列改進(jìn)算法[5-7]。基于小汽車出行最短路徑算法，李文勇[8]針對(duì)于公共交通利用Di jkstra算法通過(guò)線路激素強(qiáng)度的更新機(jī)制，實(shí)現(xiàn)了以換乘次數(shù)最少和公交出行站點(diǎn)最少的公交出行路徑選擇優(yōu)化目標(biāo)。許倫輝[9]基于蟻群系統(tǒng)中對(duì)最優(yōu)路徑信息素的加強(qiáng)和對(duì)次優(yōu)路徑信息素的揮發(fā)并行正反饋的機(jī)制，設(shè)計(jì)出求解公交出行最優(yōu)選擇路徑算法。（2）基于圖論的公交出行最短路徑選擇算法。這類算法將公交系統(tǒng)抽象建模成一個(gè)以公交站點(diǎn)為節(jié)點(diǎn)、以線路為連線的圖，基于圖論搜尋公交出行換乘方案。A?ez首先提出的二重圖公交網(wǎng)絡(luò)模型[10]。蘇愛(ài)華[11]針對(duì)公交網(wǎng)絡(luò)換乘問(wèn)題構(gòu)造了公共交通網(wǎng)絡(luò)模型，將站點(diǎn)及經(jīng)過(guò)這些站點(diǎn)的線路構(gòu)成換乘矩陣進(jìn)行搜索。楊新苗[12]利用了地理信息系統(tǒng)（GIS）中站臺(tái)聯(lián)接邊表，通過(guò)公交站臺(tái)表以及站臺(tái)經(jīng)過(guò)線路表示公交網(wǎng)絡(luò)，并且用GIS方向估價(jià)函數(shù)搜索節(jié)點(diǎn)的相鄰站點(diǎn)，建立了公交乘客出行路徑選擇模型。傅冬綿[13]把圖論中針對(duì)單個(gè)節(jié)點(diǎn)的廣度優(yōu)先搜索思想推廣到擁有若干個(gè)節(jié)點(diǎn)集合的廣度優(yōu)先搜索，提出了換乘最少路徑選擇算法。（3）考慮換乘次數(shù)、換乘等待時(shí)間和票價(jià)等綜合因素的公交出行路徑選擇算法。Nicholas[14]提出了公交網(wǎng)絡(luò)靜態(tài)多路徑選擇算法，其中以換乘次數(shù)最少為第一目標(biāo)，出行距離最短為第二目標(biāo)。Jolliffe[15]研究得出換乘等待時(shí)間的隨機(jī)性隨公交車發(fā)車時(shí)間間隔的增加而降低。基于此，后續(xù)研究人員建立了一系列考慮換乘等待時(shí)間的路徑選擇模型[16-18]。趙巧霞[19]建立了以換乘次數(shù)最少為主要目標(biāo)，途經(jīng)站數(shù)最小為次要目標(biāo)的最優(yōu)路徑出行模型。并設(shè)計(jì)了廣度優(yōu)先算法。何勝學(xué)[20]考慮了公交線路票價(jià)的變化對(duì)乘客出行路徑的選擇的影響，并且對(duì)等車時(shí)間進(jìn)行了量化改進(jìn)，以降低算法的復(fù)雜度。

綜上所述，基于小汽車交通最短路徑算法，結(jié)合公交線網(wǎng)，研究人員建立了一系列綜合考慮了換乘次數(shù)、出行時(shí)間等因素的公交出行路徑選擇模型。但現(xiàn)有方法多以單個(gè)公交線路及換乘出行鏈為搜索目標(biāo)，將不同的公交線路作為不同的公交出行路徑方案進(jìn)行比選，忽略了公交共線運(yùn)行這一常見(jiàn)特征。而實(shí)際乘客出行中當(dāng)兩站點(diǎn)間存在多條公交線路時(shí)，會(huì)選擇最先到達(dá)的線路。因此，有必要改進(jìn)以往算法中將不同公交線路完全作為競(jìng)爭(zhēng)關(guān)系的處理方法，考慮共線運(yùn)行時(shí)不同公交線路的合作關(guān)系，從而給乘客提供更為合理、全面的公交出行路徑。

本文以此為切入點(diǎn)，為解決以往未考慮公交共線運(yùn)行，造成公交線路選擇不合理的問(wèn)題，提出了一種基于站點(diǎn)及共線運(yùn)行的公交乘客出行路徑選擇方法，通過(guò)搜尋合理的換乘站點(diǎn)，將途經(jīng)站點(diǎn)間的所有共線公交線路作為乘客可乘坐的線路。

2 模型構(gòu)思

從上述文獻(xiàn)綜述看出，以往研究中公交出行路徑多以單個(gè)公交線路及換乘出行鏈為搜索目標(biāo)，將不同的公交線路作為不同的公交出行路徑方案，分別計(jì)算出行時(shí)間，進(jìn)行比選。如圖1所示，由起點(diǎn)A至終點(diǎn)F備選的公交出行方案包括：（1）R1線換乘R3線，換乘點(diǎn)為C或D或E；（2） R1線換乘R4線，換乘點(diǎn)為E；（3） R2線換乘R3線，換乘點(diǎn)為D或E；（4） R2線換乘R4線，換乘點(diǎn)為E。按上述備選方案進(jìn)行比選，便將不同公交線路完全作為競(jìng)爭(zhēng)關(guān)系進(jìn)行處理。

圖1 模型構(gòu)思

而實(shí)際公交乘客最合理的出行方案應(yīng)當(dāng)是在A站乘坐R1或R2線路，然后在E站換乘R3或R4線路。為此，本算法將以換乘站點(diǎn)選擇為基礎(chǔ)，將兩站點(diǎn)間的線路作為合作關(guān)系，從而最終公交出行路徑方案由最優(yōu)換乘站點(diǎn)及換乘站點(diǎn)間可選擇線路集構(gòu)成。由于在公交站點(diǎn)有多條線路可供選擇，大大減少了乘客等車時(shí)間，提高了公交出行的便利性和效率。

具體出行時(shí)間包括兩部分：（1）車外時(shí)間，指乘客到達(dá)站點(diǎn)時(shí)間和在站點(diǎn)等車時(shí)間，在等車時(shí)間計(jì)算中將考慮可選線路集的線路數(shù)及各線路發(fā)車頻率；（2）車內(nèi)時(shí)間，根據(jù)可選線路集中各線路行程時(shí)間，以發(fā)車頻率為權(quán)重，加權(quán)平均確定。

3 模型算法

3.1 優(yōu)化目標(biāo)

本研究以換乘次數(shù)最少為首要優(yōu)化目標(biāo)，出行時(shí)間最小為次要優(yōu)化目標(biāo)，即首先選擇換乘次數(shù)最少的路徑集，在相同的換乘次數(shù)下選擇出行時(shí)間最短的路徑。

3.2 網(wǎng)絡(luò)描述

站點(diǎn)層面：H表示公交站點(diǎn)集合；i表示公交站點(diǎn)，i∈H；Hj表示公交線路j沿線的站點(diǎn)集合，Hj?H。

公交線路層面：R表示公交線路集合；j表示公交線路，j∈R；Ri表示途經(jīng)公交站點(diǎn)i的線路集合，Ri?R；Ri,i'表示途經(jīng)公交站點(diǎn)i和站點(diǎn)i'的線路集合，Ri,i'?R；Rn表示第n層潛在換乘站點(diǎn)所有線路的集合。

3.3 算法步驟

Step 1：初始化起訖點(diǎn)o、d，換乘次數(shù)n=0，進(jìn)入Step 2。

Step 2：確定途經(jīng)起點(diǎn)o的線路集合R0和途經(jīng)終點(diǎn)d的線路集合Rd，R0=R0，進(jìn)入Step 3。

Step 3：搜尋直達(dá)線路集Ro,d，若R0|Rd=?，進(jìn)入Step 4，否則進(jìn)入Step 7。

Step 4：確定換乘次數(shù)和潛在換乘站點(diǎn)，具體步驟包括：

Step 4-1：換乘次數(shù)加1，n=n+1，進(jìn)入Step 4-2。

Step 4-2：確定第n層潛在換乘站點(diǎn)集合Hn，如式（1）所示，進(jìn)入Step 4-3。

Step 4-3：確定途經(jīng)第n層潛在換乘站點(diǎn)所有線路的集合Rn，如式（2）所示，進(jìn)入Step 4-4。

Step 4-4：搜尋從第n層潛在換乘站點(diǎn)至終點(diǎn)的線路集，若Rn|Rd=?，返回Step 4-1，否則進(jìn)入Step 5。

Step 5：記錄總換乘次數(shù)m=n，進(jìn)入Step 6。

Step 6：回溯整個(gè)換乘過(guò)程，確定可行換乘站點(diǎn)，具體步驟包括：

Step 6-1：確定第n層可行換乘站點(diǎn)集Hpn，如式（3） 所示，進(jìn)入Step 6-2。

Step 6-2：進(jìn)入前1層，n=n-1；若n≥1，返回Step 6-1，否則進(jìn)入Step 7。

Step 7：確定可行的公交出行路徑，由起始站點(diǎn)o，各層可行換乘站in∈Hpn的組合，以及終點(diǎn)d構(gòu)成，進(jìn)入Step 8。

Step 8：確定各條可行公交出行路徑的出行時(shí)長(zhǎng)，由各站點(diǎn)的等車時(shí)間和站點(diǎn)間行程時(shí)間組成，具體步驟包括：

Step 8-1：計(jì)算路徑k第n層站點(diǎn)至第n+1層站點(diǎn)的公交線路集合，如式（4）所示，進(jìn)入Step 8-2。

Step 8-2：計(jì)算路徑k第n層站點(diǎn)的等車時(shí)間期望值。如式（5）所示，式中假設(shè)公交到達(dá)滿足泊松分布[21-23]，則乘客的等車時(shí)間服從負(fù)指數(shù)分布，公交線路單位時(shí)間發(fā)車數(shù)量為λj，進(jìn)入Step 8-3。

Step 8-3：計(jì)算路徑k第n層站點(diǎn)至第n+1層站點(diǎn)的行程時(shí)間期望值，等于兩公交站點(diǎn)間各條線路行程時(shí)間對(duì)線路發(fā)車頻率gj的加權(quán)平均值。如式（6）所示。進(jìn)入Step 8-4。

Step 8-4：計(jì)算路徑k第n層站點(diǎn)至第n+1層站點(diǎn)的出行時(shí)長(zhǎng)Tkn，如式（7）所示，進(jìn)入Step 8-5。

Step 8-5：將各站點(diǎn)間出行時(shí)長(zhǎng)累加，得到各條可行路徑的出行時(shí)長(zhǎng)，如式（8）所示，進(jìn)入Step 9。

Step 9：取各條可行公交出行路徑中出行時(shí)長(zhǎng)最小的路徑為推薦路徑，輸出結(jié)果包括各途經(jīng)站點(diǎn)以及可乘坐的公交線路，如圖2所示。

圖2 出行路徑方案示意圖

4 案例分析

以上海市軍工路周家嘴路交叉口至源深體育中心6號(hào)門公交出行為例，驗(yàn)證模型效果。

根據(jù)本文所提出的算法，首先確定途經(jīng)起始點(diǎn)的公交線路有59路、103路、124路、874路、1238路，途經(jīng)終點(diǎn)的公交線路有130路、181路、609路、775路、785路、隧道三線，因此起訖點(diǎn)間無(wú)直達(dá)的線路。然后搜尋經(jīng)過(guò)起點(diǎn)公交線路途經(jīng)的全部公交站點(diǎn)，再得到途經(jīng)這些換乘站點(diǎn)所有線路的集合，并與途經(jīng)終點(diǎn)的公交線路比對(duì)，發(fā)現(xiàn)存在共同線路，因此起訖點(diǎn)間可通過(guò)一次換乘到達(dá)。所生成的備選方案如表1所示（列舉總行程時(shí)間最小的6個(gè)方案）。其中，方案一為最優(yōu)路徑，最優(yōu)換乘站點(diǎn)為羽山路南洋涇路，從羽山路南洋涇路站至終點(diǎn)共有5條共線線路可供選擇。

表1 案例出行路徑方案

為了進(jìn)一步分析模型優(yōu)化效益，選用Di jkstra算法作為傳統(tǒng)路徑選擇模型和百度地圖作為一種較為成熟的商業(yè)路徑選擇軟件，將其與本文模型進(jìn)行比較，分別如表2和圖3所示。對(duì)比發(fā)現(xiàn)本文優(yōu)化方案總出行時(shí)長(zhǎng)較Di jkstra算法推薦方案減少19.92%，乘客在站點(diǎn)的候車時(shí)間減少了45.45%；較百度地圖推薦方案1和方案2總出行時(shí)長(zhǎng)分別減少20.70%和23.39%。進(jìn)一步對(duì)比發(fā)現(xiàn)，本文優(yōu)化模型通過(guò)選取合適的換乘站點(diǎn)，有5條線路供乘客換乘選擇（傳統(tǒng)路徑選擇模型僅提供1條），從而乘客可在該站點(diǎn)換乘最先到達(dá)的線路，優(yōu)化方案更具合理性。

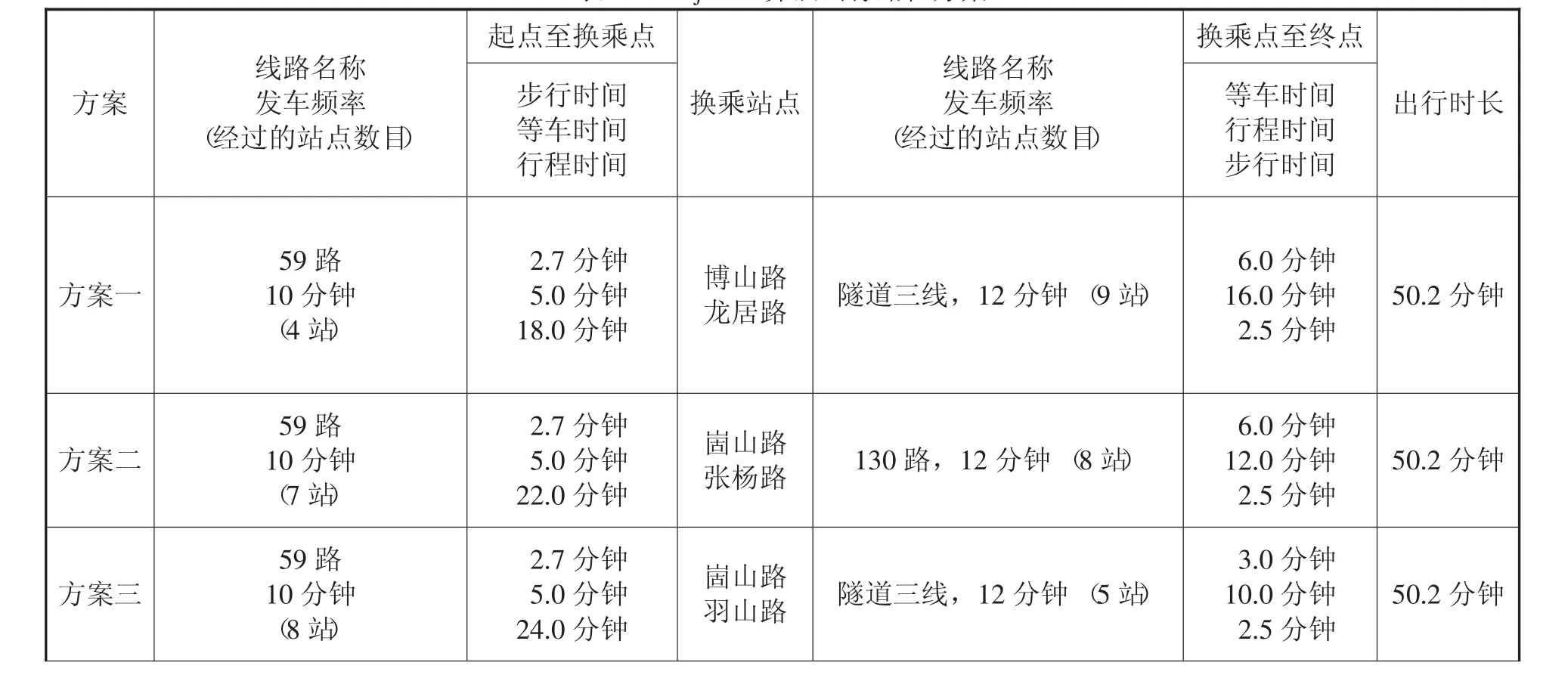
表2 Di jkstra算法出行路徑方案

圖3 百度地圖推薦路徑

5 結(jié)論

針對(duì)公交共線運(yùn)行的特征，建立了公交出行路徑選擇模型，模型具有以下特點(diǎn)：（1）改進(jìn)以往算法中將不同公交線路完全作為競(jìng)爭(zhēng)關(guān)系的處理方法，將換乘站點(diǎn)間共線運(yùn)行的公交線路作為合作關(guān)系，從而減少了乘客在站點(diǎn)的等待時(shí)間。（2）在出行時(shí)長(zhǎng)計(jì)算中，等車時(shí)間考慮了公交站點(diǎn)間所有共線線路的發(fā)車間隔，即乘客可選擇所有共線線路中最先到達(dá)的線路，有別于以往算法中僅單一線路的發(fā)車間隔；站點(diǎn)間行程時(shí)間，考慮了所有共線線路的行程時(shí)間的加權(quán)平均值，有別于以往算法中僅單一線路的行程時(shí)間，保障了優(yōu)化結(jié)果的準(zhǔn)確性。（3）通過(guò)案例分析，本文所推薦的公交出行路徑方案更具靈活性，尤其是當(dāng)某條公交線路發(fā)生故障或在上游阻塞后，乘客可靈活選擇其他線路，提高了出行可靠性，使模型計(jì)算結(jié)果更具合理性。

本文在建模計(jì)算中假設(shè)車輛到達(dá)站點(diǎn)的分布及站點(diǎn)間的行程時(shí)間均是確定的，但實(shí)際運(yùn)行中由于交通擁堵和事故，往往存在諸多不確定性，因此可將不確定性算法分析引入本模型中，提高模型的準(zhǔn)確性，有待進(jìn)一步研究。