能量有限元方法的雙星整流罩中頻聲振環境預示

王懷志，于開平，曾耀祥，王旭，張宗強

（1．哈爾濱工業大學航天學院，哈爾濱150001；2．北京宇航系統工程研究所，北京100076；3．西安航天動力測控技術研究所，西安710025）

0 引言

飛行器在飛行過程中要受到各種復雜載荷作用，對于整流罩結構來說，外部噪聲 （尤其是中高頻噪聲）對結構及內部有效載荷的影響很大，如何對這種中高頻噪聲作用下的結構進行振動環境預示是一個很重要的研究方向。

對于目前的振動環境預示來說，常用的有基于單元類的有限元 （FEM）和邊界元 （BEM）方法，基于能量意義的統計能量方法 （SEA）以及混合類方法。而能量有限元方法 （EFEA）是近些年來出現的一種基于能量的，主要用于中高頻振動環境預示的方法，它集合了單元類方法和能量類方法的優點，能夠較好解決單元類方法在高頻域帶來的計算量問題，同時對結構的不確定性問題不敏感，相對于傳統的能量類方法又能夠考慮能量在結構上的分布。

EFEA屬于功率流類方法［1］，Nefske等［2］最早基于波動理論建立了簡單梁結構的能量密度控制方程。此后，能量有限元的研究經過較多的發展，目前在工程上已經有一定的應用，Zhang等［3］將能量有限元方法應用于某潛艇結構，Vlahopoulos等［4］對復合材料艙體結構進行了能量有限元分析，并與實驗結果進行了比較，獲得了較好的結果。在國內，孫麗萍等［5］將能量有限元方法應用于某簡化護衛艦的機座結構，徐福慧［6］采用能量有限元方法對某齒輪箱結構的振動特性進行了研究，林毅［7］對某導彈艙體結構進行了研究。EFEA還有其他的一些應用，包括游進等［8］對耦合板結構進行了研究，陳書明等［9］對聲腔和板耦合系統進行了研究，并與SEA和實測值進行了比較。

對于衛星整流罩結構，目前主要的研究采用統計能量分析方法，如孫目等［10］采用SEA方法對某整流罩結構進行了噪聲環境預示，王昆［11］采用SEA方法研究了整流罩結構的聲振特性，宋海洋等［12］采用SEA方法對火箭整流罩的減振降噪問題進行了研究。此外，趙小見等［13］采用有限元方法對整流罩結構在噪聲下的腔內噪聲分布進行了研究，但是其結果只在低頻內有效，朱衛紅等［14］采用混合法 （FE－SEA）對整流罩－衛星－儀器艙－適配器的組合體進行了預示，通過與實驗數據比較驗證了預示方法和結果的有效性。

綜上所述，目前能量有限元方法在解決復雜問題，尤其是在航天領域的一些復雜結構的應用極少，且現有的應用都是將復雜結構簡化為很簡單少數板梁結構耦合系統，難以對更為復雜的結構如衛星整流罩結構進行預示。而傳統采用的有限元方法無法解決中高頻的預示問題，SEA方法只能給出子結構的平均響應信息，即使是混合方法 （如FE－SEA），對于聲腔內部以及部分關注部位的響應也無法給出。

鑒于此，本文基于能量有限元方法，建立了雙星整流罩的EFEA模型，并借助于NASTRAN的EFEA模塊，對該復雜結構的動力學環境預示，并得到了符合預期的預示結果。

1 板的能量有限元理論

在穩態下，對于圖1所示的單元體，其能量流平衡方程［13］為式 （1）。

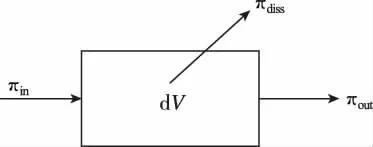
圖1 單元體的能量流Fig．1 The energy flow of the unit element

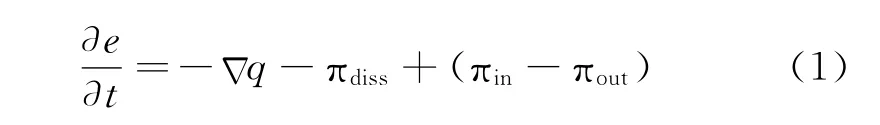
在式 （1）中，e表示結構的能量密度，q表示功率流 （單位時間內流經單位邊界尺寸上的能量），πdiss＝ηω〈珋e〉表示結構損耗的能量，πin表示結構的輸入能量，πout表示結構傳遞給其他系統的能量，（πin－πout）表示單元體的凈輸入能量，對于沒有能量交互的單系統來說，凈輸入能量為πin，后文的公式推導主要對單系統來進行。

根據 Nefske等［2］的假設以及對梁［14］和板［15］的能量流關系的推導可知，能量密度與能量流的關系類似于熱傳導的關系，即

式 （3）中，η為結構的內損耗因子，Cg為結構的群速度，考慮穩態情況時這樣可以得到板的能量密度平衡方程。

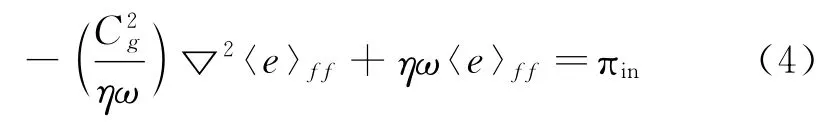
其中，〈e〉ff表示對能量密度進行空間和單個頻率周期內做平均，根據Galerkin加權余量方法，可以得到能量有限元方法的方程。

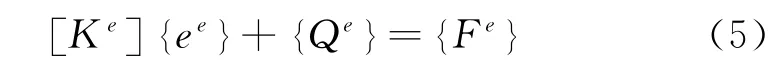
假設權函數為Nii＝1，2，…，m（

），

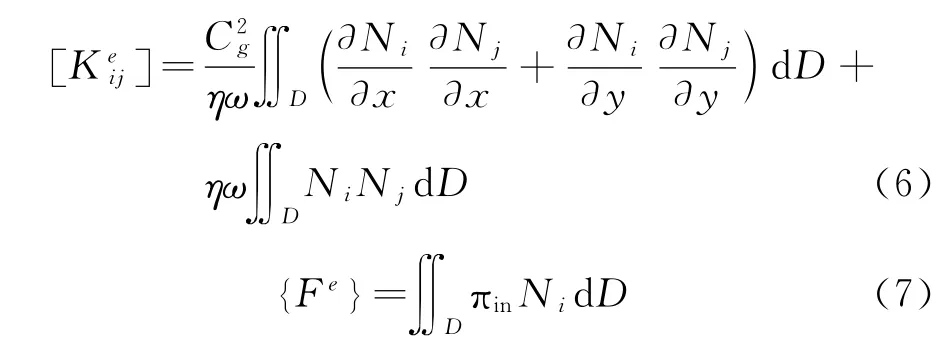
其中，［JCe］的表達式為［3］：

結構和聲的能量密度與其均方根速度值滿足以下關系：

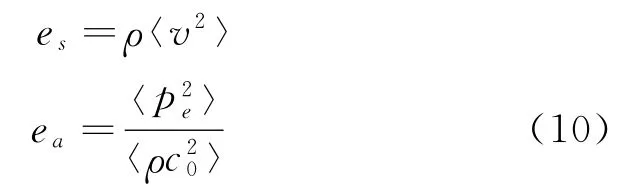
式 （10）中，es表示梁板結構的能量密度，〈v2〉表示對應結構的速度的均方值，ea表示聲腔的能量密度，pe表示聲壓的有效值，〈p2e〉表示聲壓有效值的均方值，c0表示當前狀態下的聲速。

根據統計能量分析中關于統計平均的理論［17］，速度與位移和加速度的均方值具有以下關系：

〈d2〉、〈v2〉和〈a2〉分別表示頻帶內位移、速度和加速度的均方值，ωn表示頻帶中心頻率對應的角頻率。根據式 （10）和式 （11）可以通過能量密度得到帶寬內位移、速度和加速度的均方值。

對于能量有限元方法的上限頻率，可以由式（12）給出［18］：

其中，l為結構的特征長度。

2 NASTRAN中EFEA模塊的應用

MSC．NASTRAN的EFEA模塊是目前可以使用的商用能量有限元方法模塊，主要用來解決中高頻域的復雜結構的振動、聲振耦合等問題。該模塊可以建立桿、梁、板、噪聲單元以及相互之間的耦合，可以對復合材料、加筋結構進行建模，可以模擬結構吸聲、焊點、接縫以及湍流邊界等復雜特性。

利用MSC．NASTRAN進行EFEA分析主要包括5個步驟 （如圖2所示）：前處理 （建立有限元模型）、EFEA預處理、能量有限元建模、EFEA分析以及后處理。

圖2 MSC．NASTRAN進行EFEA分析流程Fig．2 MSC．NASTRAN EFEA analysis flow chart

建立有限元模型需要借助MSC．PATRAN或者Hypermesh等有限元建模軟件，有限元模型建立以后，對于輸出的bdf文件采用pre－efea模塊進行前處理，可以得到處理后的文本格式的模型文件，在該模型文件的基礎上進行EFEA建模，需要對結構的載荷、分析頻帶、材料、阻尼損耗因子等參數進行建模，并添加出控制等信息［19－20］，已經完成的EFEA模型文件如圖3所示。

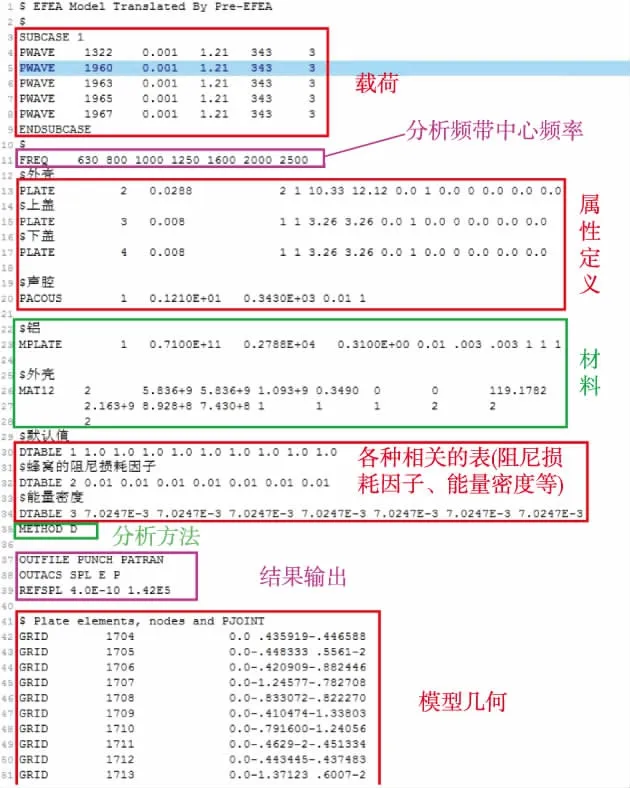
圖3 進行EFEA分析的模型文件結構Fig．3 The structure of the EFEA model file

圖3中給出了進行能量有限元分析的文本格式模型文件，模型需要定義載荷、分析頻帶、材料屬性、損耗因子以及輸出等幾個部分，這與VAOne對SEA的建模具有很大的相似性。各種屬性采用NASTRAN的卡片［21－22］來指定，卡片參數的定義與SEA中的參數定義保持一致。

分析結果可以輸出結構能量密度、均方根速度等，聲腔的能量密度、聲壓的均方根以及聲壓級，結果文件可以直接輸出文本、PUNCH文件、Matlab直接識別的MAT文件以及可以導入PATRAN進行后處理的文件 （輸出類型選PATRAN）。

3 在整流罩結構中的應用

本文采用能量有限元方法對某雙星整流罩結構進行了振動環境的預示，該結構示意圖如圖4所示。

圖4中標注了雙星整流罩的主要結構，各艙段之間的連接段有加強框 （圖4中未標注），上星支架、上星過渡支架和上星將整流罩結構分成兩段。根據上述簡化結構對該雙星整流罩進行有限元建模，得到結構的有限元模型如圖5所示。

在建模的時候，殼體部分采用三角形單元，內部聲腔采用了四面體單元，因為能量有限元模塊要求殼體和聲腔之間的單元節點耦合起來以方便在對應位置生成實體－殼之間的耦合連接，對于較復雜的結構劃分成四面體單元和三角形單元較為容易。

考慮到在實驗過程中，整流罩底部固定在基礎上，下星支架、下星過渡支架和基礎之間也構成一個小的聲腔，所以該模型建模時實際上包含3個聲腔。根據實際情況，需要對3個聲腔進行建模。聲腔的聲壓級是工程上非常關注的事項，也是本文動力學環境預示的一個主要內容。

在整流罩結構中，外部所有的殼體、上下衛星支架以及上下衛星過渡支架為蜂窩夾心結構，對該結構的建模采用三明治夾心理論進行了簡化，采用EFEA模塊的夾層板單元屬性進行建模。尾部倒錐部分為加筋板結構，采用EFEA的加筋板屬性進行了相關的建模工作。

該整流罩結構置于外部聲場中，通過對結構的能量傳輸關系進行分析，得到能量流傳遞路徑，如圖6所示。

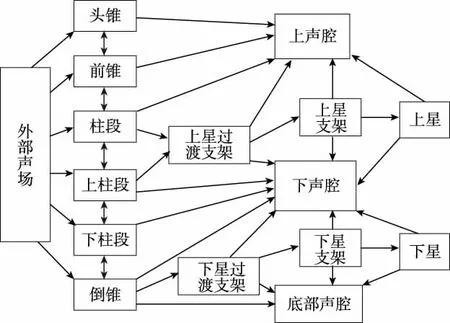
圖6 能量流傳遞路徑Fig．6 The schematic diagram of the energy flow between subsystems

在能量傳遞的過程中，子系統本身還具有能量的損耗，即結構的內損耗因子和耦合損耗因子部分。

然后分析整流罩結構的能量傳輸路徑，從圖6可以看出，能量主要通過外部殼體以及上下星支架和過渡支架部分傳遞到內部聲腔，結構部分相互連接之間存在能量的交換，根據圖6的能量傳遞關系，可以建立如圖7所示的整流罩統計能量分析模型。

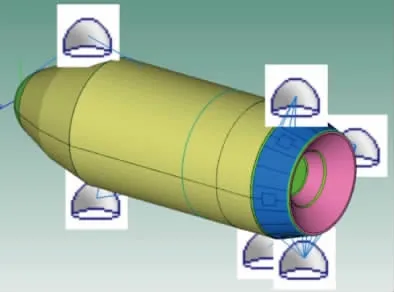
圖7 雙星整流罩SEA模型Fig．7 The SEA model of the fairing structure

根據該雙星整流罩結構，考慮材料屬性的差異，將該結構劃分為70個統計能量子系統，其中有3個聲腔子系統，7個半無限大聲場，60個板殼子系統。半無限大聲場與雙星整流罩外部殼體部分連接，模擬外部殼體與外部聲場之間的能量輻射，混響場激勵采用VA One中的Diffuse Acoustic Filed進行建模。

4 整流罩結構的EFEA分析

整流罩外殼受到混響場聲壓激勵，其聲壓級（Sound Pressure Level，SPL）曲線如圖8所示。

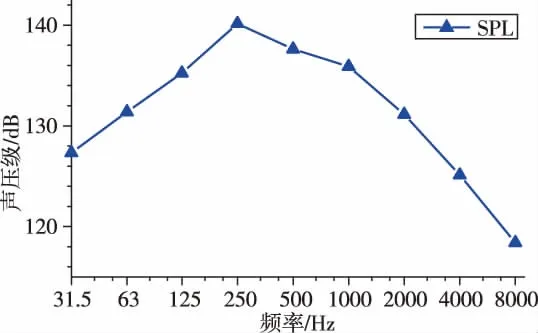
圖8 整流罩聲場的聲壓級曲線Fig．8 The SPL curve of the sound field

阻尼損耗因子一般情況下需要通過實驗的方式測得，由于條件的限制，本文中的模型不能得到基于實驗驗證的阻尼損耗因子，文中結構的內損耗因子設置參考了文獻 ［21］的公式。而耦合損耗因子則基于NASTRAN的EFEA模塊和VA One分別自動計算得到。

對該整流罩結構進行EFEA分析，可以得到上下聲腔的聲壓級響應結果，如圖9～圖12所示。

本文中的實測數據來源于對整流罩進行混響聲場的實驗。實驗時，整流罩豎直置于混響場中心，底部由橡膠墊支撐，支撐墊的頻率低于分析頻率的下限。

圖9 上聲腔上端聲壓級Fig．9 The SPL of the top of the upper cavity

圖10 上聲腔下端聲壓級Fig．10 The SPL of the bottom of the upper cavity

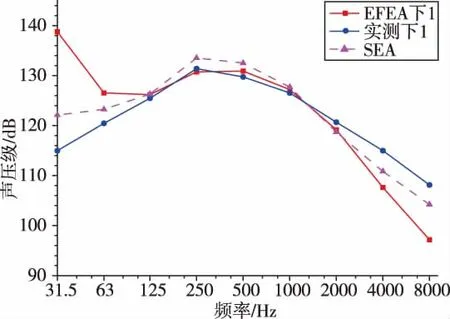
圖11 下聲腔上端聲壓級Fig．11 The SPL of the top of the lower cavity

圖12 下聲腔下端聲壓級Fig．12 The SPL of the top of the lower cavity

比較可以發現，在頻率較低時，采用SEA和EFEA預示結果與實測值相差較大，在125Hz～2000Hz的頻段內，EFEA的預示結果與實測值相比誤差基本小于3dB，大于2000Hz時誤差開始增大。本文模型及其仿真結果得到的EFEA方法更適合中頻段的動力學環境預示問題，這與EFEA方法的理論以及之前的理論驗證結果是相符的。

與實驗值的比較可以發現，在低頻段兩種方法都出現了較大的誤差。這是由于在低頻時，子系統的模態疊合數 （Modal Overlap）很小，而能量類方法采用了頻帶和空間上統計平均，其引入的誤差會變得很大；在125Hz～2000Hz范圍內，兩種方法都得到了基本符合要求的預示結果，其中，能量有限元方法的結果與實測結果更為接近。

整流罩結構部分進行EFEA分析后，得到的1000Hz頻段的均方根速度分布云圖，如圖13所示。

圖13 用PATRAN顯示的結構的速度均方根分布Fig．13 The RMS distribution of the structure by PATRAN

圖13采用了半剖視圖，顯示了整體結構的均方根速度分布，通過云圖可以得到關注結構速度值極值的位置，這是能量有限元方法相對統計能量分析方法的一個優勢。

在本結構中，測點主要分布在頭錐、前錐、柱段、上星支架、上星過渡支架、上柱段、下柱段、倒錐、下星支架、下星過渡支架等結構的上下部位。仿真值與實測值對比如表1所示。

在表1中，采用20×log10 （P／P實測值）計算得到均方根加速度以dB為單位的相對誤差。從表中的數據對比可以發現，采用SEA和EFEA兩種方法得到的結果在大部分位置上相比差別不大，與實測值相比，兩種方法大部分測量位置的加速度響應基本滿足工程要求，但EFEA方法能夠得到更加精細的響應分布信息。此外，考慮到能量有限元方法在連接部分能量密度是不連續的，而統計能量分析方法是對子系統進行平均的結果，所以在連接部分實際上也是理論上產生較大誤差的位置。綜上考慮，采用EFEA對整流罩進行的振動環境預示基本符合預期。

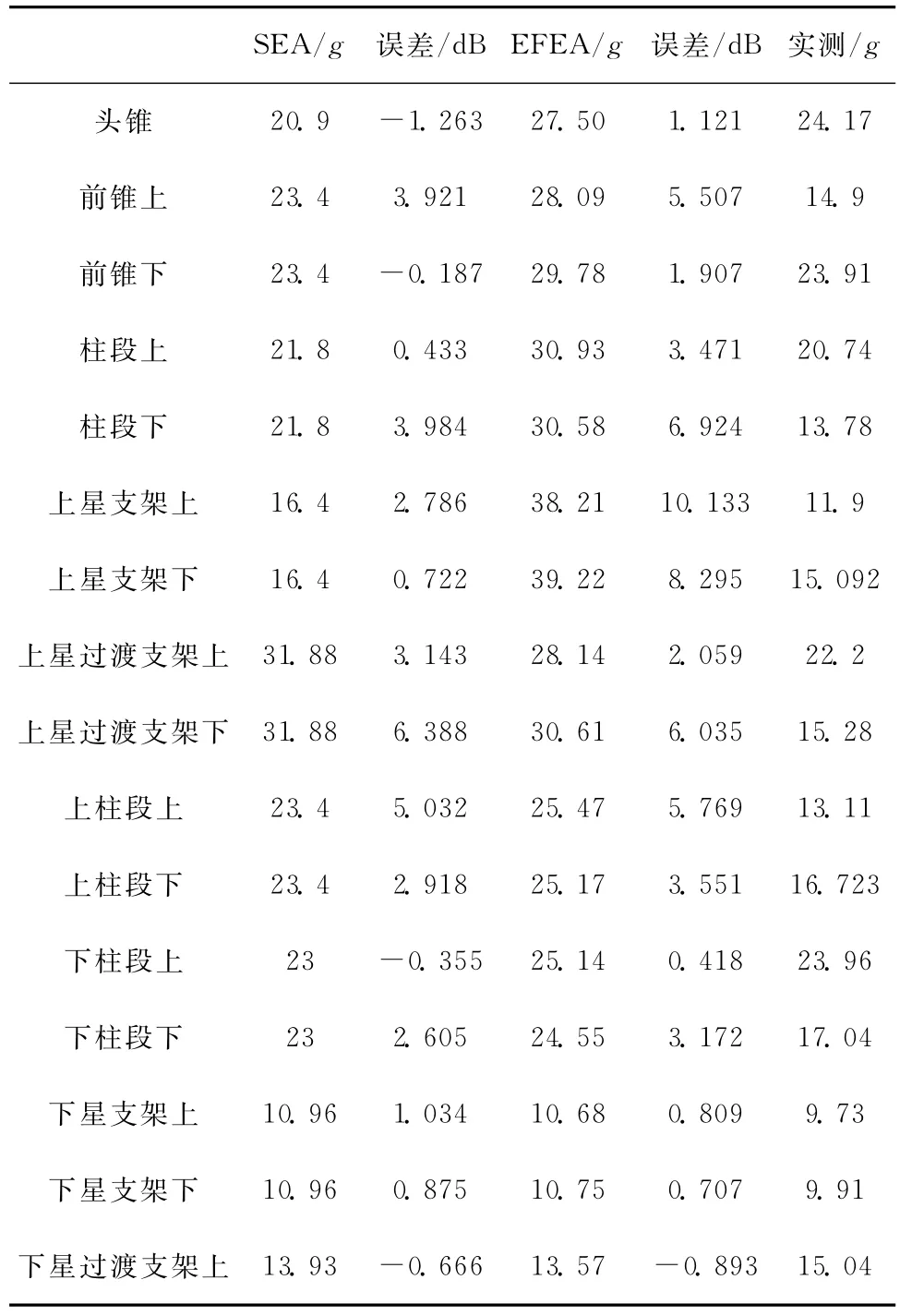
表1 主要結構部分的均方根加速度值比較Tab．1 The RMS of the Acceleration of the main structure

此外，通過對3種尺度模型，采用SEA和EFEA方法進行了計算效率的比較，模型及計算耗時如表2所示。

表2 兩種方法計算耗時比較 （單位：s）Tab．2 Computation time costs of SEA and EFEA （unit：s）

從理論上來說，計算的頻帶數和子系統數目決定了SEA方法的計算耗時，而EFEA方法則與計算頻帶數與模型的節點數／自由度數相關，EFEA方法的計算耗時大于SEA方法，這與理論預期是相符的。有限元方法的計算耗時取決于模型的自由度數，且有限元方法和EFEA方法進行求解使用的求解器是相同的，理論上來說自由度數相同時，兩者的計算耗時應該是相近的，所以本文未單列出有限元的計算耗時。但是對于相同的模型，EFEA方法由于可以劃分更為粗略的網格，因而理論上可以很大程度上減少有限元方法的計算量。

5 結論

本文采用EFEA方法，建立了某雙星整流罩結構的能量有限元模型，同時建立了該結構的SEA模型，完成了該結構的振動環境的預示，通過對EFEA、SEA方法的預示結果與實驗測試結果的比較可知，采用能量有限元方法可以較好地完成復雜工程結構在中間頻段內的振動環境預示工作，且相對于SEA方法，EFEA可以得到預示結果的空間分布。在本文中，將EFEA方法運用到較為復雜的實際工程結構，并給出了采用NASTRAN中EFEA模塊進行能量有限元建模的方法，可以為后續該方法的研究以及在航天工程中的進一步應用提供一定的借鑒。