新型控制系統穩定性分析方法研究與展望

楊曉靜

（北京航空航天大學航空科學與工程學院，北京100191）

0 引言

穩定性分析是現代飛行器總體設計及其控制系統開發過程的重要環節［1］，線性定常穩定性量化指標，如相位裕度 （Phase Margin，PM）和增益裕度 （Gain Margin，GM）［2］已經廣泛應用并成為飛行控制律設計的基本準則之一。然而，基于線性數學變換的穩定性裕度不能適應含有如大范圍傾側角或攻角指令、大范圍狀態變化、系統相關參數快變等因素造成的飛行器軌跡跟蹤系統的快變屬性的穩定性分析。事實上，線性定常系統控制理論經常將非線性、時變因素視為不確定性，將設計出來的控制器應用在非線性時變系統中時，這些控制器不是處在危險的臨界狀態，就是在性能和穩定性方面過于保守［3］。復雜飛行器的制導控制系統尚缺乏針對非線性時變系統，類似相位裕度和增益裕度這樣廣泛使用的標準。而隨著非線性控制理論的深入研究和非線性方法在飛行器控制的實驗及工程實踐中越來越多的應用［4－7］，對非線性時變系統建立像相位裕度和增益裕度這樣成熟的穩定性測度標準變得日益緊迫重要。

2008年以來，以攝動分析方法為基礎，奇異攝動裕度 （Singular Perturbation Margin，SPM）和 廣 義 增 益 裕 度 （Generalized Gain Margin，GGM）作為適用于非線性時變系統穩定性測度和量化評估標準在美國控制會議上被提出，科研工作者逐步開發了針對半適定、慢時變、線性定常和非線性定常等系統類型的兩類新的穩定裕度的計算方法［8－10］，并在仿真和實驗中驗證了概念建立和計算方法的有效性。

這兩種新的穩定裕度針對非線性時變飛行控制系統及其控制律設計，作為先進飛行器對于非標稱的操作、高危險動作及其對復雜和劇變環境容納能力的標準，有潛力成為一項飛行控制律評估與確認技術［11］中的一項基本準則，既能保證飛行控制策略在飛行條件快速變化時對穩定性要求進行必要響應，又能從穩定性定量分析的角度對飛行器難度任務和復雜環境決定的高風險飛行狀態進行預先風險評估診斷，在設計階段充分考慮和挖掘飛行器執行任務的飛行潛力，在復雜飛行控制系統總體設計迭代過程中，切實提高控制系統的安全性和可靠性。

1 定義

1．1 奇異攝動裕度

線性定常奇異攝動系統 （受擾系統）表達為［12］

其中，A11、A21、A12和A22為常數矩陣，ε為奇異攝動參數，z（t）和x（t）分別為快、慢系統狀態變量。當ε→0，受擾系統變為標稱系統。

定義1［9］：對線性定常受擾系統，奇異攝動參數ε可定義為

其中，ωBW，nom、ωBW，fast和ωcg，nom分別為標稱系統帶寬、快系統帶寬和標稱系統穿越頻率。奇異攝動裕度，記為εmax，定義為使受擾系統式 （1）臨界穩定的快系統最小帶寬ωBW，fast。

定義1中，εcl和εlg分別為從閉環系統帶寬之比和環路增益的角度定義線性定常系統的奇異攝動參數ε，而對非線性時變系統，奇異攝動裕度可由定義2表達。

定義2［10］：非線性時變標稱系統記為

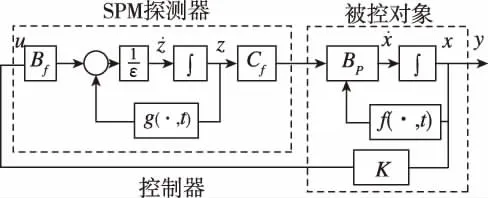
圖1 非線性時變奇異攝動系統示意圖Fig．1 The diagram of a nonlinear time－varying singular perturbation system

1．2 廣義增益裕度

定義3［9］：線性定常標稱系統記為

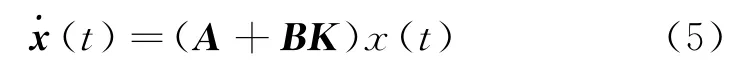
其中，A、B、K是常數系統矩陣。廣義增益裕度，記為kmax和kmin，分別定義為標稱系統的奇異攝動裕度為0時，系統增益的增加和減少。

定義4［10］：非線性時變標稱系統記為

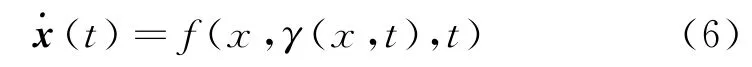
奇異攝動裕度作為相位裕度在非線性時變系統中的擴展，與相位裕度具備一一對應關系，這一關系的嚴格證明參見文獻 ［9］。類似線性定常系統相位裕度與增益裕度之間的關系，廣義增益裕度概念由奇異攝動裕度定義，廣義增益裕度對線性定常系統的分析方法與增益裕度等價，計算線性定常系統的廣義增益裕度只需調用計算機計算增益裕度的函數。

2 基本性質

奇異攝動裕度和廣義增益裕度與相位裕度和增益裕度的關系如下：

1）對線性定常系統，奇異攝動裕度和廣義增益裕度分別相對相位裕度和增益裕度具備等價性；

2）相位裕度和增益裕度是單維結構，奇異攝動裕度和廣義增益裕度是立體結構；

3）相位裕度和增益裕度基于傳遞函數和頻率域分析，數值結果單一，只應用于線性定常系統，奇異攝動裕度和廣義增益裕度可以進行頻率域分析，也可以進行時間域分析，數值結果多元，可用于線性定常系統，也可以應用于線性時變系統和非線性系統。

圖2和圖3以二維軌跡為例解釋了奇異攝動裕度和廣義增益裕度的上述性質，及其與相位裕度和增益裕度的異同。

圖2和圖3中所用符號意義如表1所示。傳統方法 （相位裕度和增益裕度）與非線性時變軌跡穩定性分析比較如表2所示。

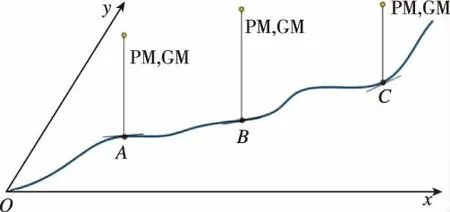
圖2 沿軌跡控制系統穩定性分析示意圖（相位裕度PM和增益裕度GM ［9］）Fig．2 The diagram of the control system stability analysis，PM and GM，along the trajectory

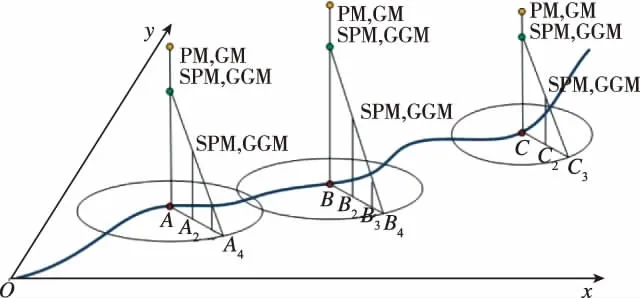
圖3 沿軌跡控制系統穩定性分析示意圖（奇異攝動裕度SPM和廣義增益裕度GGM）Fig．3 The diagram of the control system stability analysis，SPM and GGM，along the trajectory

表1 圖2和圖3中所用符號意義Tab．1 Meanings of the symbols in Fig．2and Fig．3

表2 傳統方法與非線性時變軌跡穩定性分析比較Tab．2 The comparison of trajectory stability analysis between the classic method and nonlinear time－varying method

3 實例：高超聲速飛行器控制系統穩定性定量分析

高超聲速飛行器的飛行包線大，飛行特性復雜，外部環境多變，其動態特性呈現強非線性、強不確定性和強時變性，對于這種復雜情況，傳統相位裕度和增益裕度的計算不僅僅存在保守性的問題，而是有可能得到完全錯誤的分析結果［3］。本節給出相位裕度和奇異攝動裕度的分析比較。

3．1 問題提出

高超聲速飛行器主要結構不確定性為質量m、轉動慣量Iy、彈性模態頻率ωi、大氣密度ρ、飛行器參考面積S、平均氣動弦長珋c、重力加速度g、前后彈性變形角Δτ1和Δτ2、氣動參數和控制輸入等，主要非結構不確定性為未建模彈性模態。按照攝動標準分為奇異攝動和正則攝動。高超聲速飛行器不確定性的分類如表3所示。

考慮飛行器沿軌跡飛行時的質心平移環路的穩定裕度，即在三自由度質心平移環路中，增加三自由度姿態控制環路，即攻角和側滑角的跟蹤動態 （如表3所示，該環路對質心平移環路為奇異攝動），再入飛行器制導控制系統 （軌跡跟蹤）如圖4所示。

表3 高超聲速飛行器不確定性分類Tab．3 Uncertainty classification of hypersonic vehicles

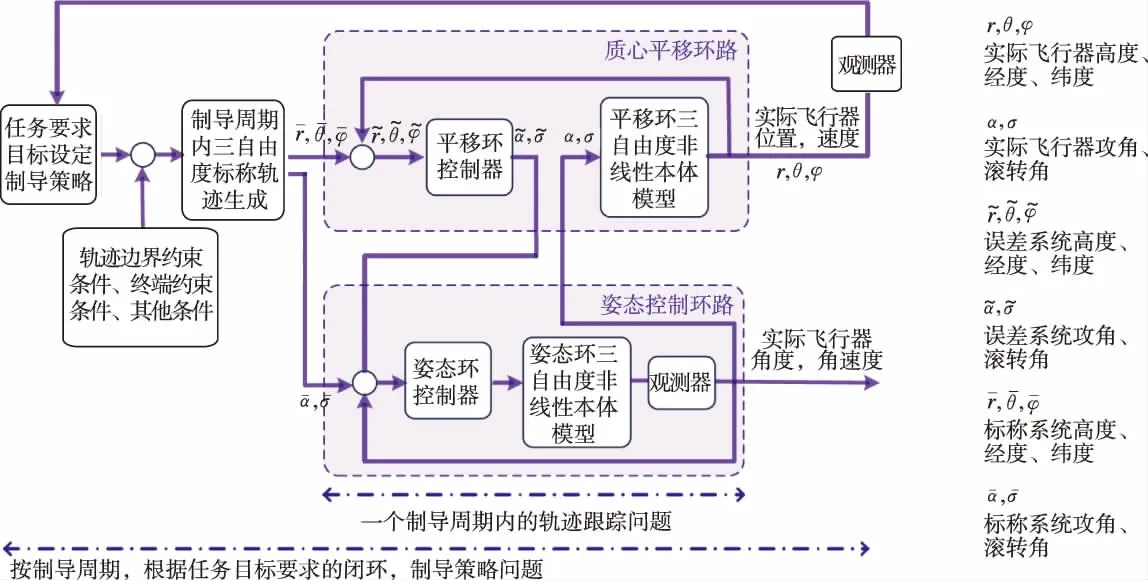
圖4 再入飛行器制導控制系統 （軌跡跟蹤）Fig．4 Re－entry Vehicle guidance control systems （trajectory tracking）

已知參考軌跡：

1）參考軌跡各個狀態量的數值，時間 （s），距地面高度 （m），經度 （°），緯度 （°），軌跡傾角 （°），航向角 （°），速度 （m／s），攻角 （°）、速度軸滾轉角 （°）和距地心高度 （m），如圖5和圖6所示。

2）沿參考軌跡的線性化系統矩陣序列Ai和Bi；

3）三自由度縱向控制反饋矩陣序列Ki。

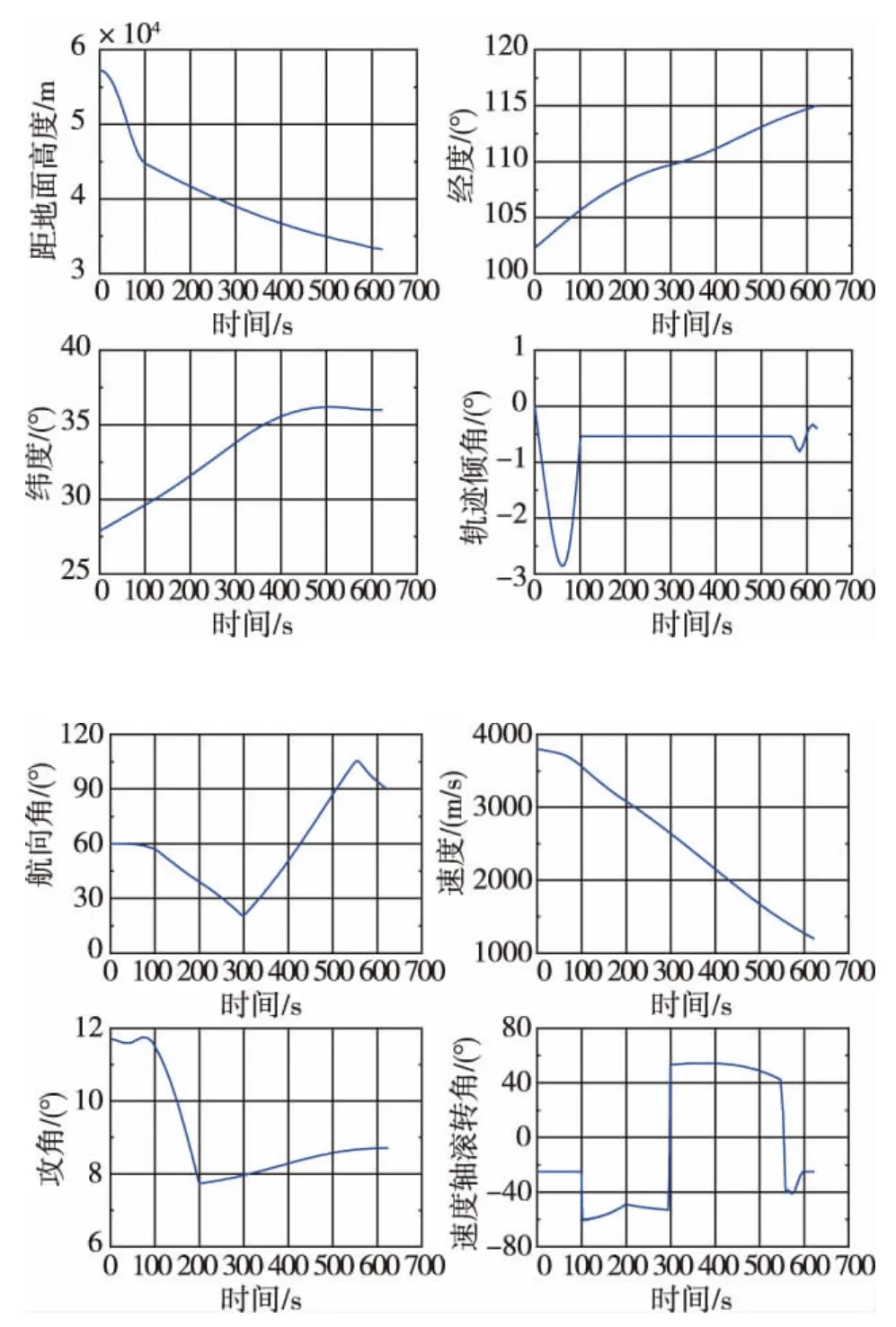
圖5 參考軌跡Fig．5 Reference trajectory

圖6 高度速度參考軌跡Fig．6 Reference trajectory in altitude and velocity

3．2 相位裕度分析

沿軌跡線性化系統矩陣A（t）、B（t）在時間點ti的數值可求得導數矩陣（t）、（t）在時間點ti的數值，系統矩陣 A（t）、B（t）及其導數矩陣（t）、（t）的大小由其范數表征，各矩陣二范數如圖7所示。

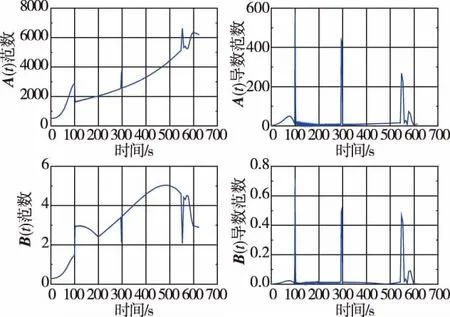
圖7 系統矩陣及其時間導數矩陣范數Fig．7 The norm of system matrices and its time derivative matrices

由圖7可見，飛行器系統A（t）、B（t）在100s左右，300s左右和550s左右3個時間點發生了較快變化，對比圖5參考軌跡的滾轉角圖像，這3處變化對應標稱軌跡中控制狀態速度軸滾轉角的快變時刻。下面考察翻轉過程系統的快速變化對穩定性和穩定裕度的影響。如圖8所示，飛行器系統矩陣在280秒至320秒呈現快變狀態，系統矩陣導數發生快速變化。

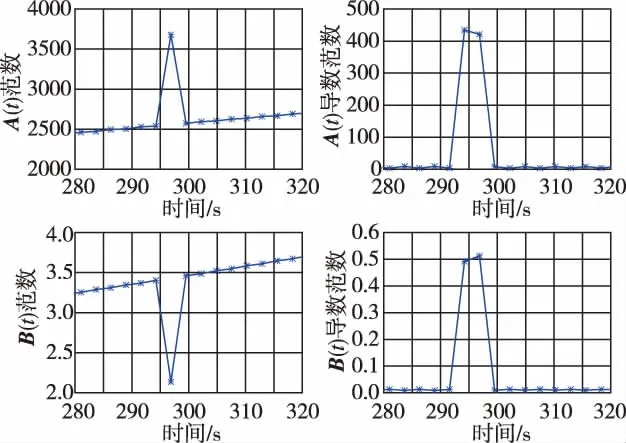
圖8 系統矩陣及其時間導數矩陣范數 （280s～320s）（＊：信號點）Fig．8 The norm of system matrices and its time derivative matrices（280s～320s）（＊：signal point）

根據開環系統逐點計算閉環攻角通道的凍結時間相位裕度和增益裕度，如圖9所示。

根據開環系統逐點計算閉環穩定滾轉角通道的凍結時間相位裕度和增益裕度，如圖10所示。

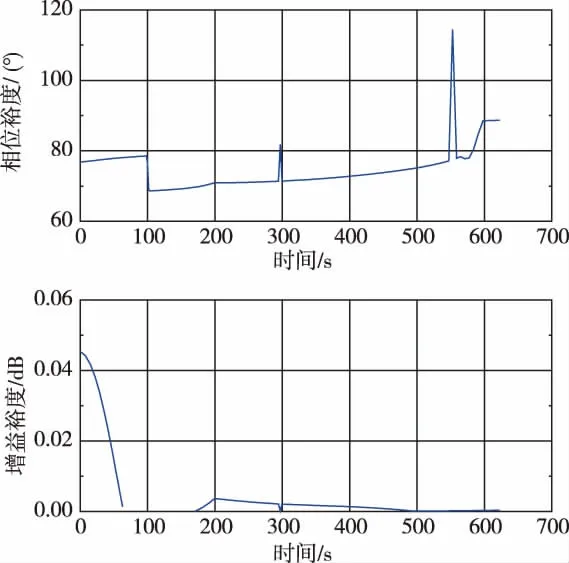
圖9 攻角通道的凍結時間相位裕度和增益裕度Fig．9 The phase margin and gain margin of the frozen time system in the angle of attack channel

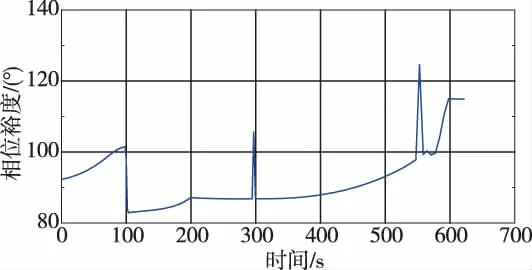
圖10 滾轉角通道的凍結時間相位裕度（增益裕度為正無窮）Fig．10 The phase margin of the frozen time system in the roll angle channel（the gain margin is positive infinity）

由圖9和圖10可見，滾轉角通道比攻角通道具有更大的相位裕度。在100s左右、300s左右和550s左右3個系統快變時刻，滾轉角通道和攻角通道的相位裕度均有增加的現象，即系統更穩定。圖9中70s～170s，增益裕度為正無窮，滾轉角通道凍結時間系統增益裕度為正無窮。

3．3 奇異攝動裕度分析

這里考察300s左右系統參數快變的情況。穩定裕度分析與控制器的設計緊密相關，每一個設計點都已經利用線性二次型調節器 （LQR）方法預先優化控制器，在下一個信號未知的情況下，采用的控制方法為凍結時間方法，一個信號周期內采用相同的增益，即基于LQR設計的凍結時間方法。在整條軌跡都預先知道，或下一個信號點預先知道的情況下，一個信號周期內采用插值進行增益調度，即基于LQR設計的插值方法。

3．3．1 凍結時間LQR方法滾轉角通道

這里選擇穩態增益為1的2階線性定常系統作為奇異攝動裕度探測器，其傳遞函數為

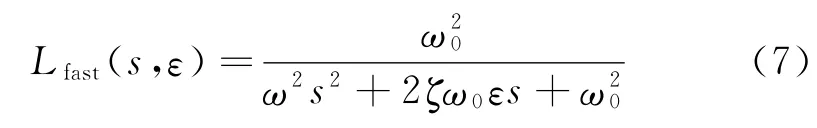
取參數ζ＝1，ω0＝2。采用凍結時間LQR控制方法并進行仿真，即在下面一個軌跡狀態點給出之前，使用前一個反饋常數矩陣Ki。奇異攝動參數為0．3時，初始誤差在速度誤差狀態和待飛航程誤差狀態震蕩的情況下，經過10s左右穩定。奇異攝動參數此處的意義在于對滾轉角的跟蹤速度，圖11顯示了奇異攝動探測器模塊前后滾轉角在奇異攝動參數為0．3時滯后的情況。

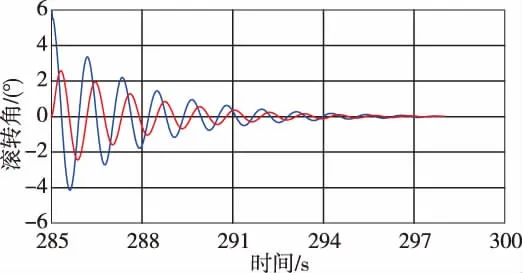
圖11 藍色：控制要求的滾轉角，紅色：滯后的滾轉角Fig．11 Blue：the roll angle of control requires，red：the lagging roll angle

由于奇異攝動探測器為2階線性定常系統，在奇異攝動參數為0．3時，信號跟蹤速度有滯后，幅值也受到一些影響。由圖11可見，滾轉角滯后約0．25s。奇異攝動參數為0．4時，系統雖然不發散，但已經失去了收斂的穩定性。因此，滾轉角通道奇異攝動裕度為0．3。

3．3．2 凍結時間LQR方法攻角通道

用類似3．3．1節的分析方法，攻角通道的奇異攝動裕度幾乎為0。奇異攝動參數為0．0001時，初始誤差其中，分別為誤差系統變量質心到地心的距離、相對于地心慣性系的速度、速度矢量與水平面的夾角、待飛航程的初始值，系統很快震蕩發散。

比較凍結時間控制設計方法下滾轉角通道、攻角通道的奇異攝動裕度分析和相位裕度分析的結果，有如下結論：

1）滾轉角快速變化時，系統穩定性略呈加強趨勢，奇異攝動裕度與相位裕度分析的趨勢相同，但相位裕度的定量差別更大。

2）攻角通道的凍結時間穩定裕度比滾轉通道小，奇異攝動裕度與相位裕度分析結論相同，但奇異攝動裕度遠小于相位裕度的數值。

3．3．3 插值LQR方法滾轉角通道

飛行器制導控制設計的參數對穩定性和穩定裕度都有影響，即穩定裕度分析與飛行器平移環和姿態環的控制器設計緊密相關。應用LQR方法時，更多地采用插值方法作為控制時間之間的過渡，這樣的過渡較凍結時間方法提高了控制器的有效性。然而，使用相位裕度和增益裕度分析，這樣的差別是不可見的。對基于LQR設計插值方法閉環控制系統進行時變穩定性量分析，選擇一階全通濾波器作為奇異攝動裕度探測器，全通濾波器具有傳遞函數形式

為比較前述凍結時間方法時，數值結果具有一致性，即對應的奇異攝動裕度在快系統跟蹤時間上可比，選擇ω0＝2。經過仿真計算，滾轉角通道奇異攝動裕度為0．21。

3．3．4 插值LQR方法攻角通道

使用類似分析方法，奇異攝動參數為0．0077時，系統處于臨界穩定的狀態。比較凍結時間LQR方法和插值LQR方法控制器設計的奇異攝動裕度，有如下結論：

1）在滾轉角通道上，凍結時間LQR方法的穩定裕度大于插值LQR方法。凍結時間LQR方法奇異攝動裕度為0．3，而插值LQR方法的奇異攝動裕度為0．21，LQR在離散時間點的插值過渡并沒有對系統滾轉角的穩定裕度有所改善。

2）在攻角通道上，插值LQR方法的穩定裕度大于凍結時間LQR方法。攻角通道上，凍結時間LQR方法控制閉環幾乎不具有奇異攝動裕度，而插值LQR方法設計控制器時，奇異攝動裕度為0．0077，對應的攻角滯后時間為0．02s。兩種控制方法下，飛行器翻轉過程并未給穩定裕度造成不利影響，反而穩定性稍好，比較圖9和圖10，這與相位裕度的分析結論相同。綜合比較兩種控制方法，從穩定性的角度，插值LQR方法好于凍結時間LQR方法。

3．4 相位裕度和奇異攝動裕度結論對比和驗證

奇異攝動裕度與相位裕度具有逐點一一對應的性質，通過該對應關系可以通過相同的奇異攝動裕度探測器，找到相位裕度對應的時間性質，即找到攻角和滾轉角通道上相應的相位裕度表征的時間滯后，并由此可以驗證相位裕度對滯后的預測是否正確，并與奇異攝動裕度的結論相比較。

選擇全通濾波器作為奇異攝動裕度探測器，全通濾波器具有傳遞函數形式 （8），與前文保持一致，這里選擇ω0＝2，當s＝j為單位純虛數，信號進入全通濾波器的時間滯后，記為Tdelay。

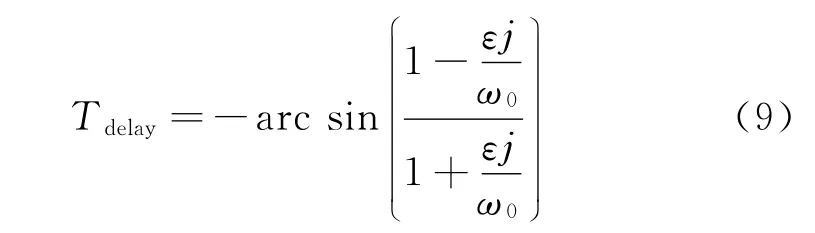
全通濾波器中奇異攝動參數為原標稱系統的奇異攝動裕度 （記為εmax）時的相位絕對值即為它所檢測的相位裕度，記為PM。

上述時間滯后Tdelay、奇異攝動裕度εmax、相位裕度PM的關系如圖12～圖14所示。

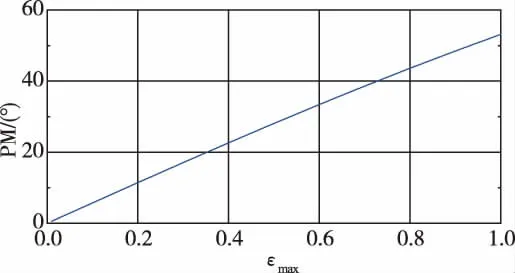
圖12 奇異攝動裕度 （εmax）與相位裕度 （PM）的關系Fig．12 The relationship between SPM and PM

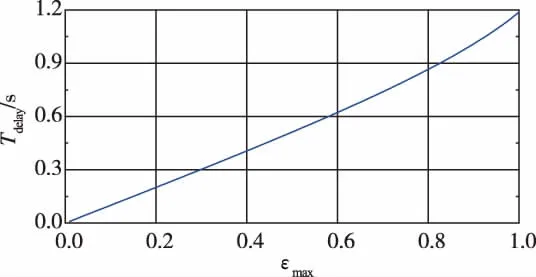
圖13 奇異攝動裕度 （εmax）與時間滯后Tdelay的關系Fig．13 The relationship between SPM and time delay

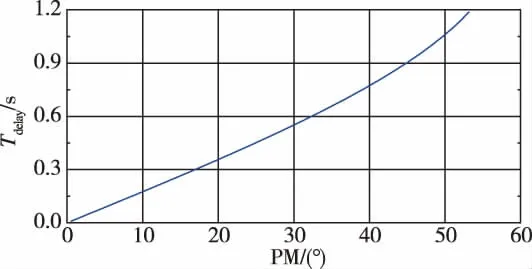
圖14 相位裕度 （PM）與時間滯后Tdelay的關系Fig．14 The relationship between PM and time delay

由圖14可知，相位裕度為50°時，相對應允許的時間滯后大于1s，然而，圖9～圖10顯示，攻角通道和滾轉角通道的相位裕度都基本大于70°，即相位裕度允許的攻角和滾轉角滯后都至少為1．2s。前文奇異攝動裕度對滾轉角通道在無其他擾動情況下估計的滾轉角允許的滯后約為0．2s，攻角允許的滯后約為0．02s。用相位裕度方法分析的結論是錯誤的。

4 結論和開放性問題

4．1 結論

1）奇異攝動裕度和廣義增益裕度是相位裕度和增益裕度在非線性時變系統中的推廣，能在非線性系統時反映出與系統多方面非線性性質具體關系，是適用于非線性時變系統穩定性量化的評估標準。

2）在高超聲速飛行器的仿真實例中，控制方法與穩定性緊密相關，而相位裕度和增益裕度分析不能反映出該相關性。沿參考軌跡相位裕度分析得到的關于姿態控制環路時間滯后的結論是錯誤的，奇異攝動裕度分析得到的結論合理，可以為進一步細化量化關聯飛行器本體參數與軌跡設計提供參考。

4．2 開放性問題

1）拓展原有基于標稱系統與快系統帶寬之比的單輸入單輸出奇異攝動裕度和廣義增益裕度概念，針對多變量飛行控制系統，建立多輸入多輸出奇異攝動裕度和廣義增益裕度概念；非線性時變穩定儲備準則相關算法優化和理論工具 （如非線性系統時變譜特征、系統特征結構以及吸引域估計）的進一步完善和推廣。

2）奇異攝動系統解耦技術在一般時變系統中的推廣。奇異攝動系統解耦方法能將奇異攝動參數以解析形式明確表達在系統解耦之后的快慢子系統中，有利于揭示穩定裕度與飛行器姿控動態特性之間的關聯機理和穩定儲備準則具體算法的進一步優化。

3）正如圖2和圖3所示，奇異攝動裕度和廣義增益裕度是立體結構，其數值是非線性系統平衡點的吸引域和吸引半徑的函數，在估計吸引半徑的方法中，Lyapunov函數方法及其優化解法是目前廣泛使用的主要方法，高超聲速飛行器制導系統和控制系統中相應吸引域和吸引半徑的最大化方法研究和應用是未來工作的一個重要部分。

4）基于已有的最小相位探測器、全通濾波器型探測器、純延遲及其Pade有理近似探測器和其它推廣形式等，進一步根據系統不確定性設計奇異攝動裕度探測器和廣義增益裕度探測器。尤其是對具體機型的參數不確定性的分布情況，美國國家航空航天局做了大量以計算機仿真為核心的工作［13］。以高超聲速飛行器系統誤差的來源、分類、分布情況等為依據設計奇異攝動裕度和廣義增益裕度探測器，以及以非線性時變系統的穩定裕度為標準的模型誤差分析依然是一個基礎而開放的問題。