基于粒子群算法優(yōu)化核極限學(xué)習(xí)機(jī)的磨煤機(jī)故障診斷

張文濤， 馬永光， 董子健， 杜景琦

(1.華北電力大學(xué) 控制與計(jì)算機(jī)工程學(xué)院，河北 保定 071003；2.云南電力試驗(yàn)研究院(集團(tuán))有限公司， 云南 昆明 650217)

0 引言

磨煤機(jī)是火電廠制粉系統(tǒng)非常重要的設(shè)備，其工作狀況對(duì)于整個(gè)火電機(jī)組的安全和經(jīng)濟(jì)運(yùn)行具有非常重要的意義，一旦磨煤機(jī)發(fā)生故障，將會(huì)影響制粉系統(tǒng)的正常運(yùn)行，其后果較為嚴(yán)重[1，2]。二十世紀(jì)八十年代之前，一般都是依靠人工分析和信號(hào)處理來對(duì)故障進(jìn)行診斷和分析，這種方法效率低且準(zhǔn)確率不高。隨著人工智能技術(shù)的不斷發(fā)展，許多機(jī)器學(xué)習(xí)方法開始運(yùn)用到故障診斷之中。支持向量機(jī)(Support Vector Machine, SVM)是一種得到廣泛應(yīng)用的機(jī)器學(xué)習(xí)算法，文獻(xiàn)[3]利用核主元分析(Kernel Principal Component Analysis, KPCA)提取特征向量，將提取后的主元作為SVM的輸入，進(jìn)行診斷和分類。此外，許多專家學(xué)者利用神經(jīng)網(wǎng)絡(luò)進(jìn)行磨煤機(jī)的故障診斷。文獻(xiàn)[4]使用RBF神經(jīng)網(wǎng)絡(luò)，但訓(xùn)練樣本過大時(shí)，訓(xùn)練速度會(huì)很慢。文獻(xiàn)[5]提出基于粗糙集(Rough Set, RS)和概率神經(jīng)網(wǎng)絡(luò)的故障診斷方法，解決了樣本維數(shù)和訓(xùn)練速度的問題，但是粗糙集理論[6，7]對(duì)數(shù)值型數(shù)據(jù)進(jìn)行離散化處理，會(huì)帶來信息損失。隨著信息融合技術(shù)的發(fā)展，許多基于D-S證據(jù)理論[8]的方法開始應(yīng)用到磨煤機(jī)故障診斷中來，文獻(xiàn)[9]將灰色關(guān)聯(lián)分析與D-S證據(jù)理論相結(jié)合，文獻(xiàn)[10]將模糊聚類分析與D-S證據(jù)理論結(jié)合，通過證據(jù)之間的相互融合，提高了故障診斷的準(zhǔn)確率。

極限學(xué)習(xí)機(jī)(Extreme Learning Machine, ELM)是由南洋理工大學(xué)的黃廣斌教授[11]在2006年提出的一種單隱含層前饋神經(jīng)網(wǎng)絡(luò)(Single-hidden Layer Feedforward Neural networks, SLFNs)的快速學(xué)習(xí)算法。ELM算法在學(xué)習(xí)過程中，無需調(diào)整網(wǎng)絡(luò)的輸入層與隱含層之間的權(quán)值和隱含層神經(jīng)元的偏置，只需要設(shè)置隱含層節(jié)點(diǎn)的個(gè)數(shù)，就會(huì)產(chǎn)生唯一的最優(yōu)解，與傳統(tǒng)的BP神經(jīng)網(wǎng)絡(luò)相比，ELM訓(xùn)練速度快且泛化能力強(qiáng)。但是，對(duì)于某些分類或者回歸問題，極限學(xué)習(xí)機(jī)往往需要較多的隱含層節(jié)點(diǎn)，且容易過擬合[12，13]。因此在此基礎(chǔ)上，黃廣斌又將核函數(shù)的思想引入到極限學(xué)習(xí)機(jī)中，提出了核極限學(xué)習(xí)機(jī)(Kernel Based Extreme Learning Machine, KELM)算法[14]。本文將KELM應(yīng)用到磨煤機(jī)的故障診斷中，并且利用粒子群算法優(yōu)化核極限學(xué)習(xí)機(jī)的參數(shù)，實(shí)驗(yàn)結(jié)果證明了本文方法的可行性和有效性。

1 核極限學(xué)習(xí)機(jī)

KELM借鑒了支持向量機(jī)[15]的思想，采用核函數(shù)來代替ELM隱含層節(jié)點(diǎn)的特征映射，與ELM相比，KELM無需人為確定隱含層節(jié)點(diǎn)的數(shù)目，只需要選擇合適的核函數(shù)參數(shù)，就能得到輸出權(quán)值。

給定N個(gè)訓(xùn)練樣本數(shù)據(jù)集(xi,ti)，其中xi=[xi1,xi2,…,xin]T∈Rn為樣本輸入數(shù)據(jù)，ti=[ti1,ti2,…,tim]T∈Rm為樣本輸出值， 對(duì)于有L個(gè)隱含層節(jié)點(diǎn)數(shù)的SLFNs，設(shè)其激勵(lì)函數(shù)為g(x)，則其網(wǎng)絡(luò)輸出為：

(1)

式中：βi為第i個(gè)隱含層節(jié)點(diǎn)和輸出層節(jié)點(diǎn)之間權(quán)值向量；ωi為第i個(gè)隱含層節(jié)點(diǎn)和輸入層節(jié)點(diǎn)之間的權(quán)值向量；bi為第i個(gè)隱含層的偏置；yj為網(wǎng)絡(luò)的輸出值。

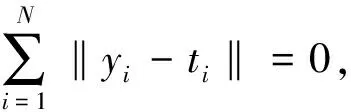
(2)

因此，上述N個(gè)方程可以表示為

Hβ=T

其中，

(3)

式中：H為隱含層輸出矩陣；T為期望的輸出向量。

通過最小二乘法確定網(wǎng)絡(luò)的輸出權(quán)值為：

β=H+T=HT(I/C+HHT)-1T

(4)

式中：H+為隱含層輸出矩陣的Moore-Penrose廣義逆矩陣；C表示懲罰因子。在矩陣HHT中加上I/C可以使其特征根偏離零，可以提高結(jié)果的穩(wěn)定性和泛化能力。

對(duì)于KELM算法，輸出函數(shù)的表達(dá)式如下：

f(x)=h(x)HT(1/C+HHT)-1T

(5)

定義核函數(shù)的計(jì)算式如下：

(6)

核函數(shù)的選擇有很多種，本文選擇RBF核函數(shù)，定義如下：

(7)

所以KELM的輸出函數(shù)表達(dá)式為

(8)

式中：γ表示核函數(shù)參數(shù)。在KELM算法中并不需要知道隱含層節(jié)點(diǎn)的特征映射函數(shù)，只要知道核函數(shù)的具體形式，就可以求出輸出函數(shù)的值。與傳統(tǒng)的ELM相比，KELM無需設(shè)定隱含層節(jié)點(diǎn)數(shù)，也不用隨機(jī)設(shè)定初始權(quán)值和偏置，因此具有更好的函數(shù)逼近能力和分類能力。

2 基于粒子群優(yōu)化核極限學(xué)習(xí)機(jī)的參數(shù)優(yōu)化算法

粒子群優(yōu)化算法(Particle Swarm Optimization,PSO)是一種群體智能算法[16，17]，其基本思想是通過群體中個(gè)體對(duì)信息的共享從而使得整個(gè)群體的運(yùn)動(dòng)在求解空間中產(chǎn)生一種有序的演變，從而獲得最優(yōu)解。所有的粒子都具有一個(gè)位置向量和速度向量，并可以根據(jù)目標(biāo)函數(shù)值計(jì)算當(dāng)前的所在位置的適應(yīng)值，在每次的迭代中，種群中的粒子通過自身的經(jīng)驗(yàn)和種群中最優(yōu)粒子的經(jīng)驗(yàn)來學(xué)習(xí)，就這樣逐步迭代，從而使得整個(gè)種群中的粒子趨于最優(yōu)解。

令Xi=(xi1,xi2,…,xin)表示粒子的位置向量，Vi=(vi1,vi2,…,vin)表示粒子的速度向量，速度和位置更新公式如下：

(9)

(10)

式中：Pbest代表個(gè)體的局部最優(yōu)位置；Gbest表示種群的全局最優(yōu)位置；ω是慣性權(quán)重；c1、c2為學(xué)習(xí)因子；r1、r2為[0,1]之間的隨機(jī)數(shù)。

慣性權(quán)值ω的調(diào)整公式如下：

ω=ωmax-t*(ωmax-ωmin)/tmax

(11)

式中：t表示當(dāng)前迭代次數(shù)；tmax為最大迭代次數(shù)。

3 基于PSO-KELM的磨煤機(jī)故障診斷方法

火電廠運(yùn)行環(huán)境復(fù)雜，而制粉系統(tǒng)磨煤機(jī)故障類別多，且難以通過故障征兆判斷故障原因。KELM算法無需設(shè)置隱含層節(jié)點(diǎn)數(shù)，且訓(xùn)練時(shí)間短，分類精度高，具有非常好的泛化性能。由于KELM引入了核參數(shù)會(huì)導(dǎo)致對(duì)參數(shù)的非常敏感[18]，因此采用粒子群算法去優(yōu)化核函數(shù)的參數(shù)γ和懲罰因子C[19，20]。基于PSO-KELM的磨煤機(jī)故障診斷方法的流程圖如圖1所示，具體步驟如下：

(1)將樣本數(shù)據(jù)分為訓(xùn)練樣本和測(cè)試樣本。

(2)對(duì)數(shù)據(jù)進(jìn)行歸一化處理。

(3)初始化粒子群算法的參數(shù)，確定組合搜索參數(shù)[C,γ]的搜索范圍。

(4)利用初始的懲罰系數(shù)C和核函數(shù)的參數(shù)γ，訓(xùn)練KELM。以樣本的分類精度作為適應(yīng)度函數(shù)，通過計(jì)算每個(gè)粒子的適應(yīng)度值不斷更新個(gè)體最優(yōu)位置和群體最優(yōu)位置。

(5)根據(jù)公式(9)、公式(10)和公式(11)，更新粒子的速度、位置和慣性權(quán)值。

(6)當(dāng)適應(yīng)度滿足條件或者達(dá)到最大迭代次數(shù)時(shí)，終止優(yōu)化過程，否則返回步驟(4)。

(7)根據(jù)尋優(yōu)得到的最佳懲罰系數(shù)C和核函數(shù)的參數(shù)γ，建立KELM故障診斷模型。

(8)利用已經(jīng)訓(xùn)練好的KELM故障診斷模型對(duì)測(cè)試樣本數(shù)據(jù)進(jìn)行故障診斷。

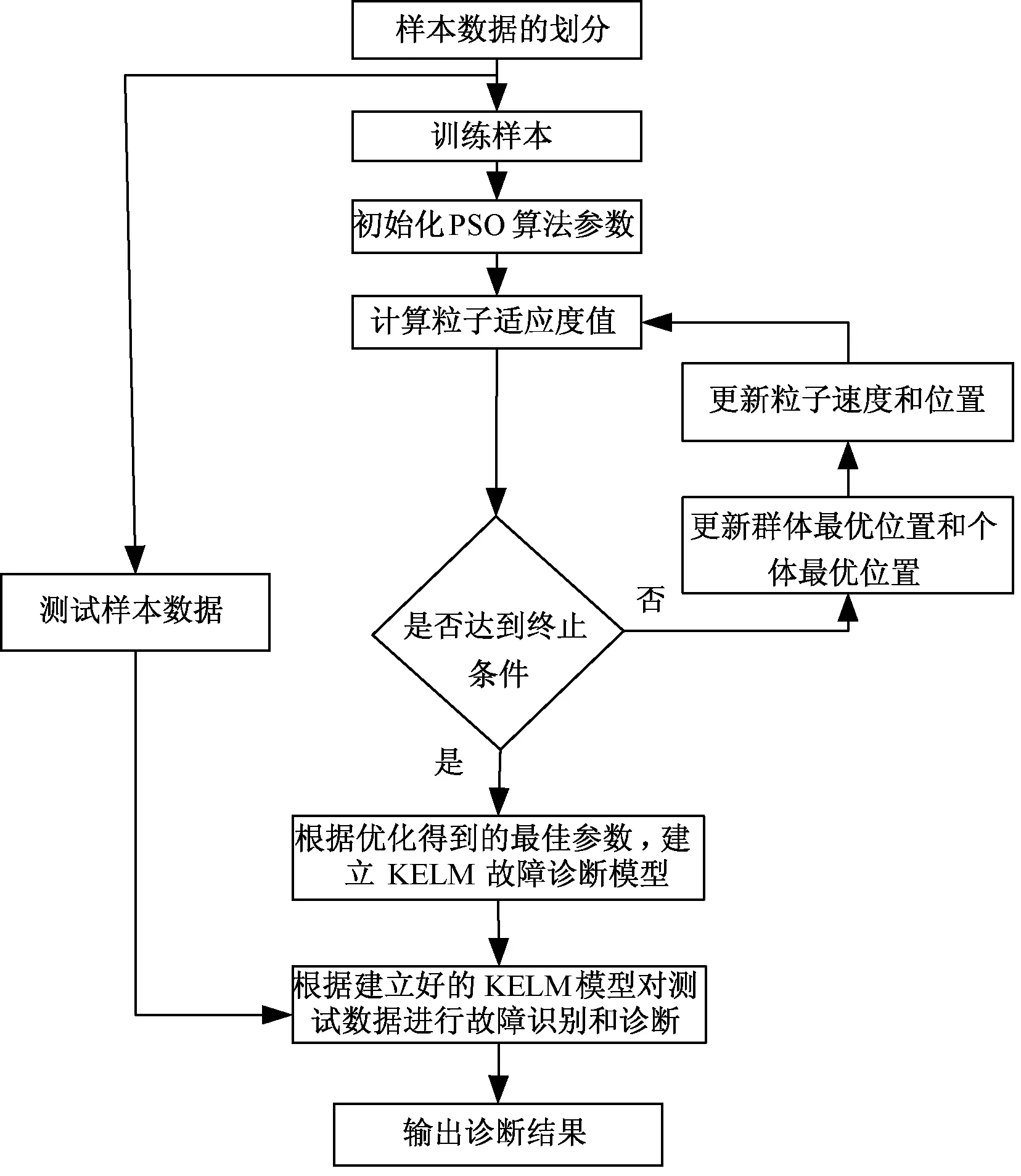
圖1 基于PSO-KELM的磨煤機(jī)故障診斷流程圖

4 實(shí)例分析

(1)樣本的選取及處理

本文以正壓直吹式中速磨煤機(jī)為研究對(duì)象，樣本數(shù)據(jù)來自于云南某600 MW機(jī)組，根據(jù)專家知識(shí)和機(jī)組以往歷史運(yùn)行經(jīng)驗(yàn)[21]，輸入?yún)?shù)選擇跟磨煤機(jī)相關(guān)的11個(gè)測(cè)點(diǎn)，分別為磨煤機(jī)電流、磨煤機(jī)齒輪箱推力瓦溫度、磨煤機(jī)潤(rùn)滑油溫度、磨煤機(jī)入口溫度、磨煤機(jī)一次風(fēng)流量、磨煤機(jī)入口壓力、磨煤機(jī)進(jìn)出口壓差、磨煤機(jī)出口溫度、磨密封風(fēng)與一次風(fēng)差壓、分離器出口壓力、給煤量。輸出參數(shù)為4種狀態(tài)，分別為正常狀態(tài)、磨堵煤、磨斷煤和煤粉自燃。一共選取160組數(shù)據(jù)，每類數(shù)據(jù)40組，數(shù)據(jù)進(jìn)行歸一化處理，消除量綱的影響，歸一化公式如下：

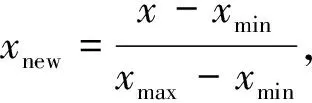
(2)模型參數(shù)的選擇

本文選擇PSO算法的參數(shù)如下：c1=c2=1.5，種群數(shù)量為20，最大迭代次數(shù)為100。經(jīng)過粒子群算法優(yōu)化KELM的參數(shù)，得到正則化參數(shù)最優(yōu)值C=23.411，核參數(shù)γ=0.685。

(3)故障診斷

仿真實(shí)驗(yàn)一共有4類數(shù)據(jù)，其中每類數(shù)據(jù)40組，每類數(shù)據(jù)的前30組作為訓(xùn)練數(shù)據(jù)，建立KELM故障診斷模型，每類數(shù)據(jù)的后10組數(shù)據(jù)作為測(cè)試數(shù)據(jù)樣本，一共有40個(gè)測(cè)試樣本數(shù)據(jù)。建立KELM故障診斷，PSO-KELM模型在測(cè)試集上的故障診斷結(jié)果如圖2所示。

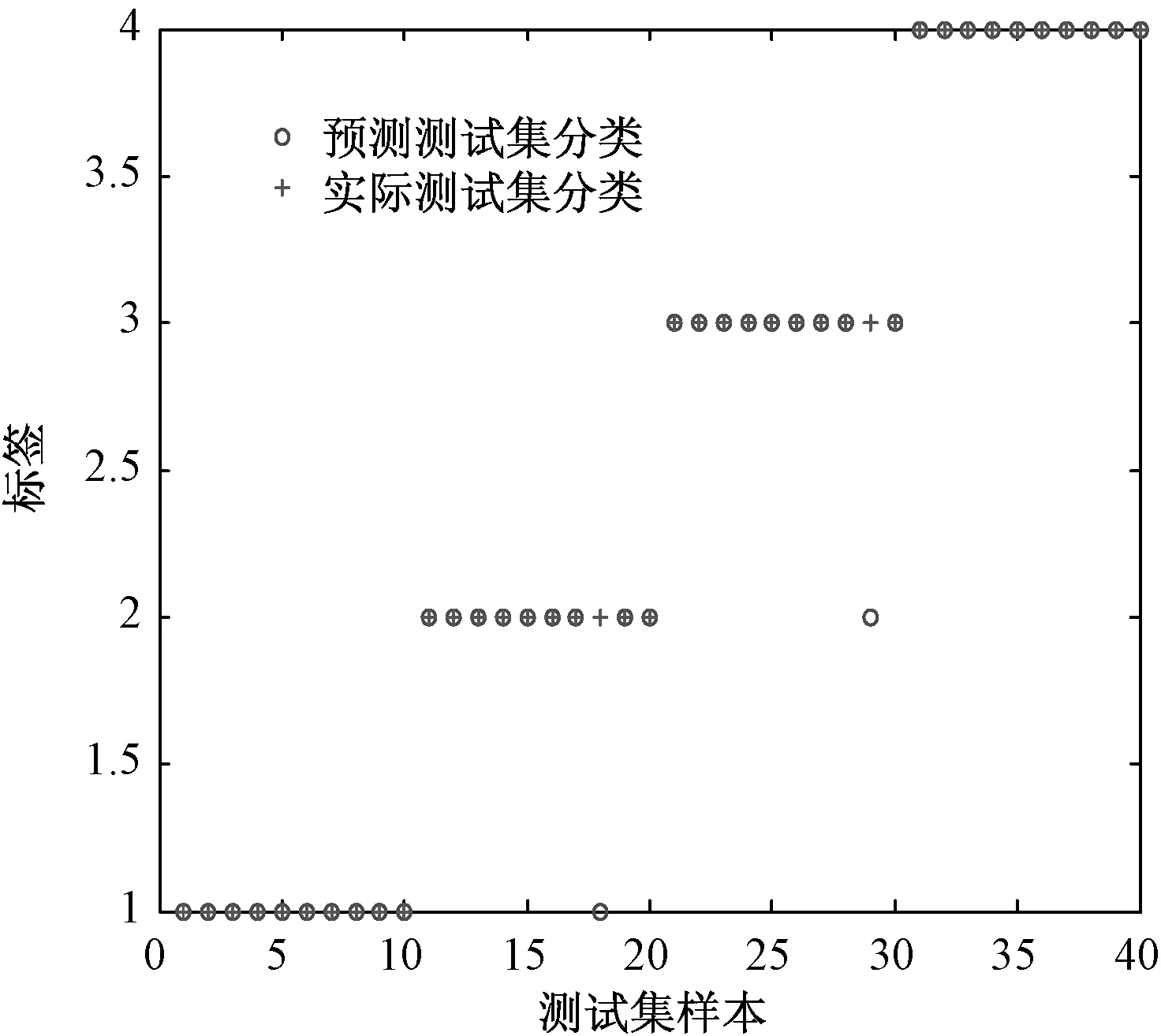
圖2 測(cè)試集樣本的故障診斷結(jié)果

從圖2中可以看出，40個(gè)測(cè)試樣本，只有2個(gè)診斷錯(cuò)誤，故障診斷準(zhǔn)確率可以達(dá)到95%。

為了進(jìn)一步驗(yàn)證本文所提方法的優(yōu)越性，再分別利用BP神經(jīng)網(wǎng)絡(luò)、SVM算法根據(jù)上文所示數(shù)據(jù)進(jìn)行磨煤機(jī)的故障診斷。其中BP神經(jīng)網(wǎng)絡(luò)的輸入層節(jié)點(diǎn)為11個(gè)，隱含層節(jié)點(diǎn)數(shù)為15個(gè)，輸出對(duì)應(yīng)4種狀態(tài)。SVM采用RBF核函數(shù)，其中懲罰系數(shù)C和核函數(shù)的參數(shù)γ通過K折交叉驗(yàn)證得到，并且采用“一對(duì)一”的多分類方式。3種方法的訓(xùn)練時(shí)間和診斷準(zhǔn)確率的比較如表1所示。

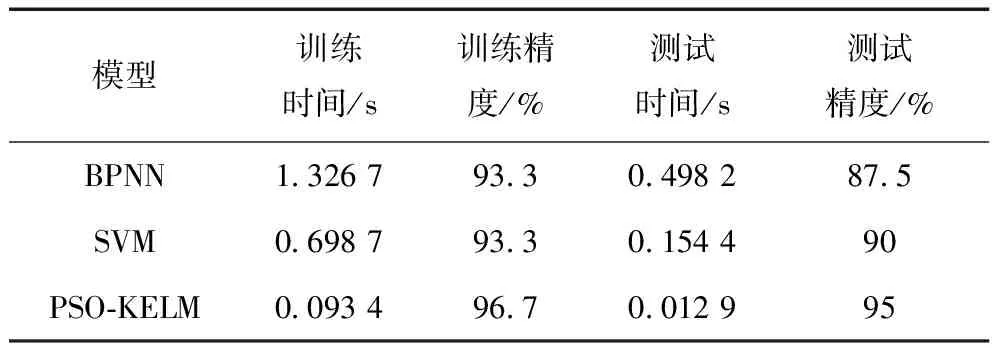
表1 診斷結(jié)果比較

從表1中可以看出，BP神經(jīng)網(wǎng)絡(luò)的訓(xùn)練時(shí)間和測(cè)試時(shí)間都是最長(zhǎng)的且訓(xùn)練樣本數(shù)據(jù)和測(cè)試樣本的分類精度分別為93.3%和87.5%。基于SVM的磨煤機(jī)故障診斷方法要優(yōu)于BP神經(jīng)網(wǎng)絡(luò)，在測(cè)試樣本上的診斷準(zhǔn)確率可以達(dá)到90%。但是很明顯，文中所提的PSO-KELM方法的效果更好，訓(xùn)練時(shí)間只有0.093 4 s，且在訓(xùn)練樣本上的準(zhǔn)確率可以達(dá)到96.7%，在測(cè)試集上的診斷準(zhǔn)確率可以達(dá)到95%。

5 結(jié)束語

針對(duì)磨煤機(jī)故障征兆多、難以確定故障類型的特點(diǎn)，本文建立了PSO-KELM的磨煤機(jī)故障診斷模型，采用粒子群算法去優(yōu)化核極限學(xué)習(xí)機(jī)的參數(shù)，利用優(yōu)化后的KELM模型進(jìn)行故障診斷。實(shí)驗(yàn)結(jié)果表明，相比于PSO-SVM等方法，本文所提方法不僅運(yùn)行時(shí)間短，而且具有更高的診斷準(zhǔn)確率。