一種基于ARMA模型的單回路控制性能評價方法

王印松， 蘇婉婉， 高 穎， 蔣雄杰， 李士哲

(1. 華北電力大學 控制與計算機工程學院，河北 保定 071003；2. 浙江浙能嘉華發電有限公司，浙江 嘉興 314000)

0 引言

工業過程中約90%的控制器都是PID控制器，其控制性能與產品質量、操作成本及生產安全都密切相關。在實際生產過程中，只有在調試階段才會對PID控制器進行參數尋優，但是隨著回路長時間的運行及現場工況的變化，控制系統性能退化，不能達到原先設計和整定時的性能。另外，一般的生產企業都有成千上百個控制回路，給維護工作帶來了一定困難。因此，評估控制系統性能以確定控制器是否需要整定十分重要。然而常規控制器整定方法一般都需要整定參數后加階躍響應，這樣耗時耗力，不適合在線分析。因此利用在線性能評估方法來確定控制器是否需要整定和維護具有很重要的意義，只需要對評估結果較差的回路進行整定，大大減少了工作量。

對于PID控制器來說，控制器性能降低的原因可能來自控制器參數的調節問題、執行機構故障或干擾等。如何對由于控制器調節不當導致的性能降低進行參數優化，是控制系統性能評價的一個重要任務。H?gglund[1]通過分析控制量和被控量，定義了IDLE指標用于診斷控制回路響應遲緩情況；Visioli[2]基于控制量定義了面積指數，診斷回路對負載擾動的響應的突發性或緩慢性；Salsbury[3]基于輸出數據響應峰的變化定義了R指數；Veronesi[4]首先估計了現有控制器的性能，然后在僅需要設定值改變的情況下完成控制器的參數調節。上述方法能夠定量地判斷控制器調節性能，但是需要在設定值或負載擾動出現大的階躍變化的情況下使用，而工業現場中，這種情況較少，不適用于系統長期在線評價。針對現場中經常受到隨機擾動的情況，Yamamoto[5]利用基于最小方差的PI系統性能評估結果對PI參數進行了在線優化控制；Goradia[6]提出一種基于系統脈沖響應曲線的方法判斷當前控制器調節遲緩/振蕩，通過迭代尋優的方法尋找PI控制器最佳性能。周猛飛[7]提出了一種基于雙層結構PID控制器的性能評估方法，第一層是基于脈沖響應曲線和最小方差準則來評估控制器的確定性和隨機性性能，接著對PID結構的控制器進行評估，該方法更符合生產實際，但需要更多的過程信息。呂書艷[8]將傳統PID控制與模糊控制算法相結合，實現PID參數的在線整定。趙洪洲[9]等提出一種多指標性能評價方法，同時評價回路的響應和設定值跟蹤情況、振蕩情況及控制器的投用情況。孫超杰等[10]采用線性二次高斯(Linear Quadratic Gaussian, LQG)基準針對PID控制回路進行了性能評價分析，并給出最優控制器。

目前，基于脈沖響應曲線評價控制系統性能的方法有很多，但在工業實際過程中利用該方法評價當前控制器參數下系統響應遲緩/振蕩的成果較少。本文利用系統單位脈沖響應函數與ARMA模型Green函數等價的特點[11]，通過對系統被控變量進行時間序列分析，得到系統單位脈沖響應曲線。根據脈沖響應曲線的性能分析系統克服隨機干擾的能力，判斷當前控制系統響應遲緩/振蕩，同時給出控制器參數優化方向。在評價過程中，系統脈沖響應曲線方法與Harris指標[12]評價結果對比驗證其有效性,同時在優化控制器參數過程中采用Harris指標作為結束標志。該方法只需要系統運行數據和遲延時間的信息，不會影響系統正常運行，適用于工業現場進行在線性能評價。

1 控制系統性能評價方法

1.1 脈沖響應曲線

脈沖響應曲線描述了噪聲序列和系統輸出之間的動態關系，可以直觀地反映控制器調節隨機干擾好壞的程度。不同于以往需要做設定值實驗得到脈沖響應曲線，本文根據自回歸滑動平均模型(Auto-Regressive and Moving Average, ARMA)Green函數即是系統單位脈沖響應的特性，通過對常規閉環運行數據進行時間序列分析即可獲得系統單位脈沖響應函數。求解脈沖響應的步驟如下：

(1)建立ARMA模型。對采集數據進行預處理[13～15]，建立ARMA模型。由于擾動信號at未知，ARMA模型參數估計的過程中會出現非線性回歸問題。而基于觀測時序建立起來的自回歸模型(Auto-regressive, AR)模型、ARMA模型是等價系統的數學模型，這兩個模型在同一時刻的殘差值at是相等的[16]。本文選用長自回歸法[17，18]建立ARMA模型，即先估算AR模型后[19]根據傳遞函數相等的規則估計出ARMA模型。該方法能夠避免ARMA模型參數估計中的非線性回歸問題。

考慮典型的單輸入單輸出控制系統，其閉環過程通過ARMA模型表示，即被控變量與擾動變量之間的關系可以表示為：

(1)

式中：φ(B)=1-φ(1)B-…-φ(n)Bn；θ(B)=1-θ(1)B-…-φ(q)Bm，且φ(B)和θ(B)無公因式；B為后移算子。

(2)計算Green函數。上述ARMA模型也可用Green函數表示為[20]：

(2)

通過式(1)和式(2)可知

(3)

在ARMA模型參數φi、θi已知的情況下，通過比較式(3)兩邊B算子的同次冪系數即可知Green函數G(j)。

(3)系統單位脈沖響應。在ARMA模型建模中，at必須為白噪聲，但模型建立后，參數φi、θi已經確定，從系統的觀點來看，at可以是任意形式的輸入，若式(2)的輸入為單位脈沖，即at=δt-j，只有在j=t時，δt-j=1。則在j=t時，

X(t)=G(t)

(4)

可以看出，G(t)是系統對t時刻作用的單位脈沖所產生的響應，即系統單位脈沖響應函數y(t)=G(t)。

脈沖響應曲線可以直觀地反映系統動態響應快慢及振蕩等信息，如果脈沖響應曲線衰減很慢，則表明有較高的可預測擾動和相對較差的控制性能；如果是快速衰減的脈沖響應曲線，則表明該系統調節很好等。因此可以通過系統的單位脈沖響應曲線計算系統響應時間和振蕩次數等，判斷當前控制器調節下系統響應遲緩/振蕩。

1.2 動態響應指標

因為系統單位脈沖響應函數是單位階躍函數對時間的導數，可以證明單位脈沖響應曲線第一次過零點的時間就是單位階躍響應曲線的峰值時間tp，即

y(tp)=0

(5)

另外，系統調節時間ts為系統單位脈沖響應曲線衰減到穩定值y(∞)的2%或5%的過渡過程時間，即當t≥ts時，

|y(t)-y(∞)|≤y(∞)*2%(或5%)

(6)

通過式(5)和式(6)可知，系統響應的第一次過零點時間tp和調節時間ts反映了系統響應速度。調節時間和峰值時間越小，系統響應的快速性越好。

此外，通過分析脈沖響應的振蕩次數可以直觀反映系統的相對穩定性。在過渡過程內，穿越穩態值的次數的一半即為振蕩次數N，通過判斷脈沖響應曲線穿越零點的次數即可求得振蕩次數。振蕩次數越多，說明系統調節過度，否則控制器調節較好或較為遲緩。

通過綜合分析脈沖響應第一次過零點時間、調節時間和振蕩次數來判斷控制器調節遲緩/振蕩，從而可以判斷控制器調節方向，通過不斷調整參數達到控制器最佳性能。

2 仿真驗證

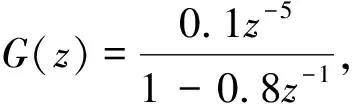
該過程采用PI控制器克服擾動，初始控制器的參數為：Kp=1.1，T=0.08。采集在該PI控制器作用下2 000個過程輸出數據，采樣時間為1 s。

根據上述性能評價方法，通過對過程輸出數據建立ARMA模型得到初始控制器參數下閉環脈沖響應曲線，并根據評價結果對當前控制器參數進行逐步優化，具體參數優化過程如圖1所示。

優化過程中系統脈沖響應曲線如圖2所示，該過程初始控制器參數下的脈沖響應曲線如曲線a所示，其Harris指標為0.559 6。曲線b、c、d是不同參數下的脈沖響應曲線。

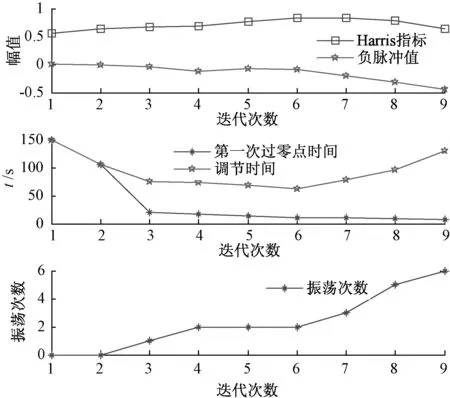
圖1 脈沖響應曲線仿真優化結果

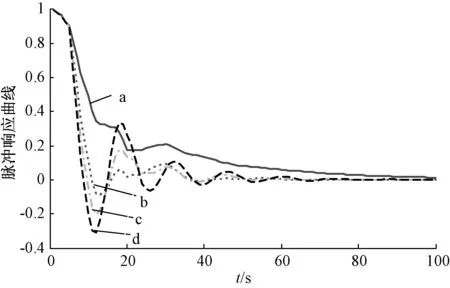
圖2 系統仿真脈沖響應曲線圖

可以看出脈沖響應曲線衰減緩慢，表明在該PI控制器作用下系統響應相對遲緩。因此，可以通過增大積分作用和比例作用加快系統響應速度。

從圖1可以看出隨著控制器參數的不斷調整，脈沖響應曲線響應速度加快，且Harris指標也逐漸增大，表明控制器優化方向是正確的。

圖1中Harris指標達到最大時為η=0.835 4，PI控制器參數為Kp=2.5，T=0.2，系統脈沖響應曲線如圖2曲線c所示，其第一次過零點時間為10 s，調節時間為78 s，振蕩次數為3，脈沖響應衰減速度較快且無較大振蕩，系統調節性能較好。此時，若比例作用繼續增大，如Kp=3，Harris指標η=0.786 5，脈沖響應曲線系統如圖2曲線d所示，調節時間增大，振蕩次數增加，系統性能明顯降低；若比例作用減小，如Kp=2，Harris指標η=0.82，脈沖響應曲線系統如圖2曲線b所示，第一次過零點時間增大，振蕩次數減小，系統性能明顯降低。因此，在Harris指標達到最大值時系統性能最佳，可以不用調整或進行細微調整達到需要的性能，與上述性能評價方法一致，該方法能夠有效地調整控制器參數，優化系統性能。

3 現場數據分析

本文將上述性能評價方法應用到某電廠#1發電機組中，從2018年1月的常規操作數據中采集爐膛壓力數據如圖3所示(采樣時間為5 s)，每兩小時計算一次系統脈沖響應曲線和Harris指標，結果如圖4所示。

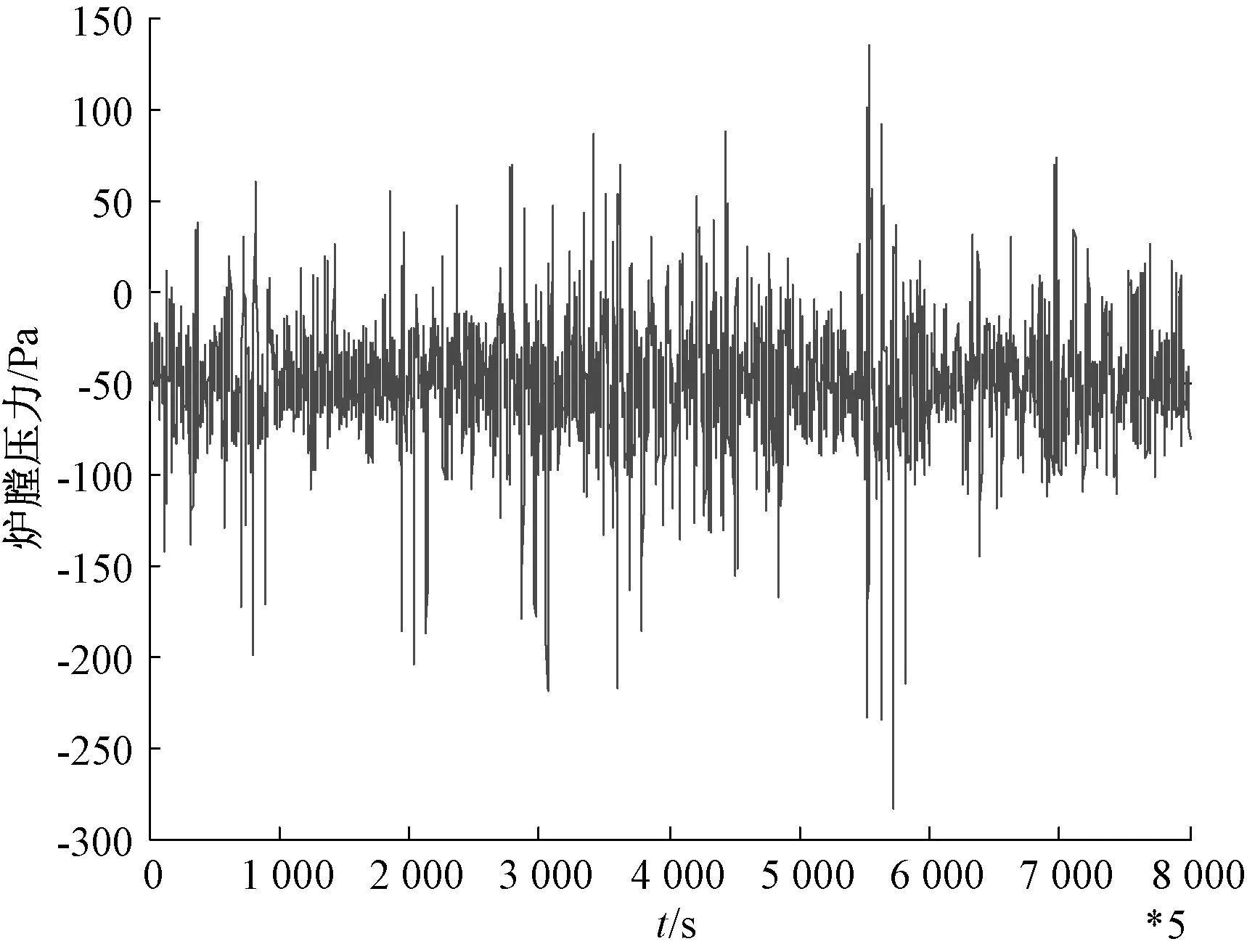
圖3 爐膛壓力輸出曲線

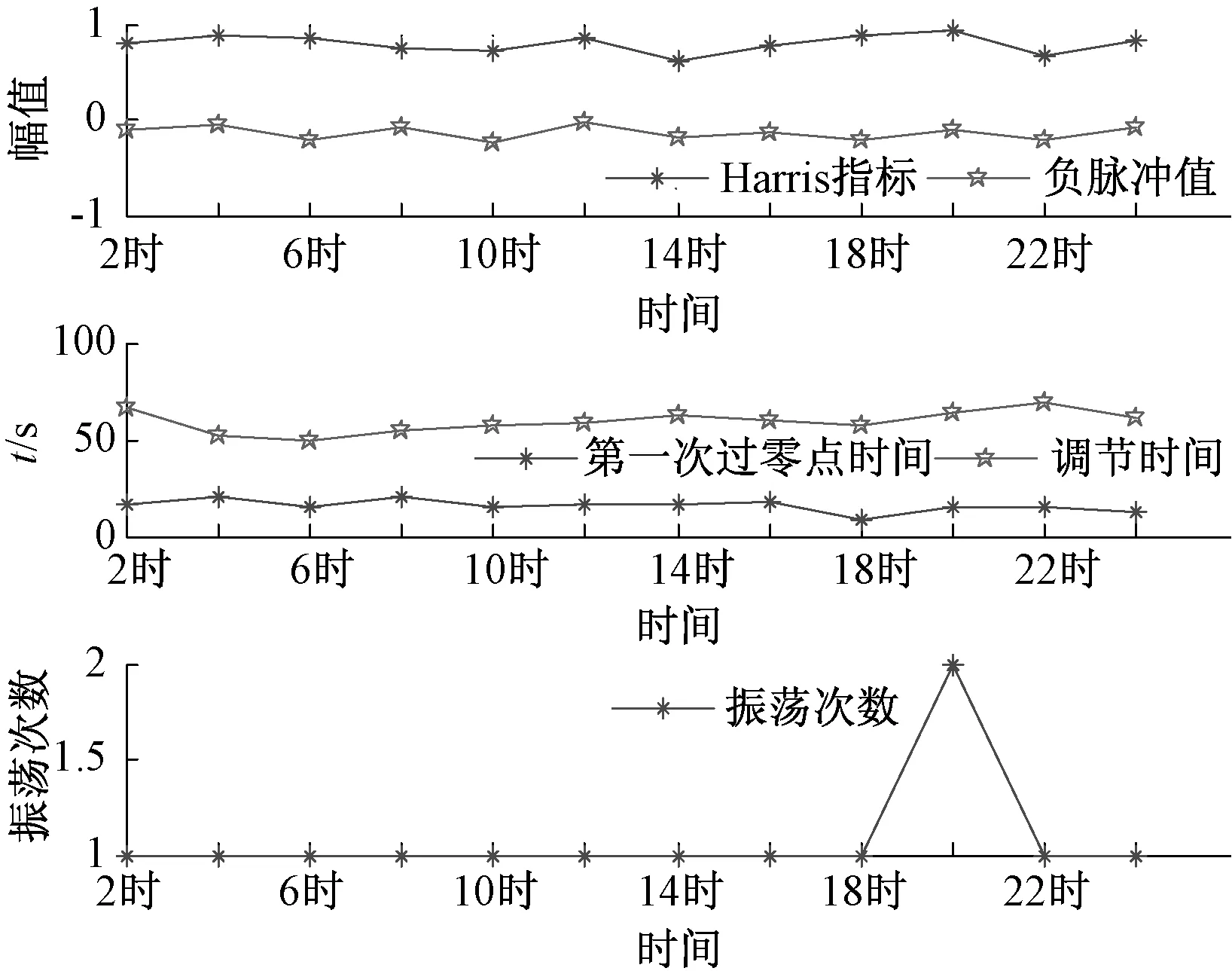
圖4 爐膛壓力脈沖響應曲線性能評價結果

可以看出，該系統脈沖響應曲線振蕩次數較少，調節時間較短，即系統響應的快速性和相對穩定性較好，系統動態性能良好，相對應的Harris指標較好，因此控制器參數不需要重新調節。

采集2018年1月的系統正常運行狀態的連排水位數據如圖5所示(采樣時間為5 s)，每兩小時計算一次系統脈沖響應曲線和Harris指標，結果如圖6所示。

圖5 連排水位輸出曲線

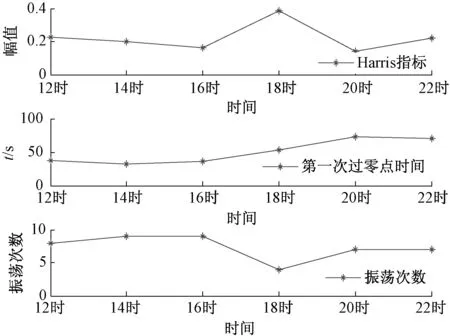
圖6 連排水位脈沖響應曲線性能評價結果

由圖6可以看出，該系統脈沖響應曲線振蕩較大，調節時間較長，即系統響應的快速性和相對穩定性較差，系統動態性能相對較差，對應的Harris指標都較差，可知當前系統性能距最佳性能還比較遠，該PI控制器的控制性能還需要進一步提高。

采集2018年1月的系統正常運行狀態的氫側密封油溫度數據如圖7所示(采樣時間為5 s)，每兩小時計算一次系統脈沖響應曲線和Harris指標，結果如圖8所示。

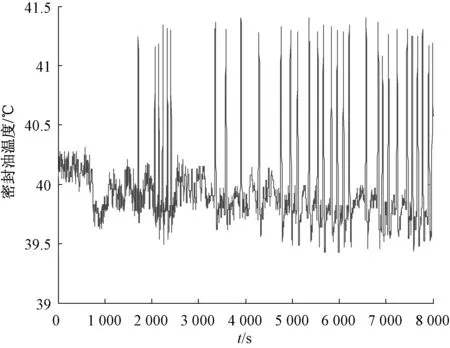
圖7 氫側密封油溫度輸出曲線

由圖8可以看出，在12時和14時系統調節時間較長，Harris指標較差，可以判斷在10時至14時時間段內該系統調節遲緩，但在之后的時間，系統響應的快速性和相對穩定性都較好，對應的Harris指標都較好。由于該系統某一段時間可能會出現調節遲緩的情況，控制器參數還沒有達到最佳參數，該系統性能還能進一步提高。通過上述分析可以看出脈沖響應曲線法分析系統性能與Harris指標一致，因此該方法能夠有效地對控制系統進行性能評價。另外，采用該方法能夠很容易的分析當前系統響應速度并給出系統優化方向，且不需要對系統做任何擾動實驗。

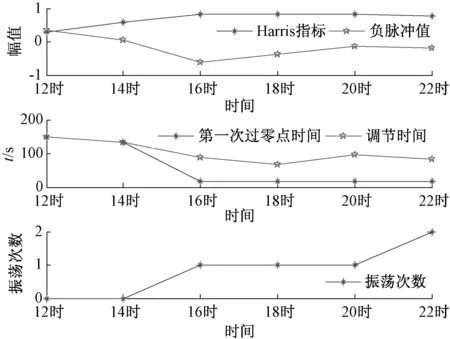
圖8 氫側密封油溫度脈沖響應曲線性能評價結果

4 結論

本文研究了基于脈沖響應曲線的方法、針對單輸入單輸出控制系統進行性能評價，通過脈沖響應曲線對當前控制器調節下的響應快速性和平穩性進行分析，可以明確控制器參數優化方向，同時在仿真過程中利用Harris指標作為參數優化的結束標志，從而避免出現調節過度的情況。該方法僅利用閉環運行數據和系統延遲時間信息，不對系統的正常運行進行額外的任何形式的擾動，易于實現，適用于工業現場控制系統的性能優化。目前，該方法還有很多不足，首先，控制器參數可能需要調整幾次才能達到最佳性能，但這是一個必須付出的代價，因為沒有一個過程模型能夠避免任何實驗，仍然能夠達到最高性能；其次，在本次工作中針對仿真回路做了性能優化研究，接下來可以針對實際工業系統進行性能優化實驗。