基于ANSYS和EDEM的小麥莖稈切割仿真研究
江 濤, 吳崇友, 湯 慶, 沐森林, 趙輔群
(1.農業部南京農業機械化研究所,江蘇南京 210014; 2.中國民航局第二研究所,四川成都 610041
我國是小麥生產大國,近年來,隨著秸稈還田的大力推廣實施,通過在聯合收割機上加裝莖稈切碎裝置將小麥莖稈切碎之后拋灑至田間已成為必不可少的作業環節[1]。國內現有與聯合收割機配套的莖稈切碎裝置的刀具結構參數和刀具有效切割速度多數依據收割機廠家的經驗來設計并確定,容易造成功耗增加、刀具使用壽命降低等結果。由于目前對切割機制及莖稈運動規律的理論研究尚有不足,仍然存在秸稈切碎效果不理想、拋撒均勻性差、易堵塞等問題。
農作物收獲受季節影響嚴重,利用仿真軟件輔助機具設計改進能夠有效地縮短研發周期,節約寶貴的試驗時間,在農業工程領域已有學者進行過切割仿真的相關研究[2-6],但是目前的研究大多采用有限元法進行分析,而該方法存在1個弊端,即無法處理大量莖稈的切割和拋灑問題,而離散單元法的思想是通過將整體的運動轉變成各個單元運動的合成,更加適合仿真模擬數量龐大、接觸碰撞頻繁且運動關系復雜的對象[7-8]。所以,筆者結合前人研究并針對上述問題,借助于有限元分析軟件ANSYS和離散元軟件EDEM(Engineering Discrete Element Method),擬對小麥莖稈沖擊式無支撐切割過程及形式進行相關分析和探討并建立莖稈離散元模型,以期對為后續的莖稈群體仿真提供研究基礎,也能夠為全喂入聯合收割機莖稈切碎裝置的設計提供一定的理論依據和參考。
1 仿真試驗條件
1.1 試驗材料
本研究選用楊麥17號小麥品種作為試驗對象,莖稈的力學特性參數如下:密度為600 kg/m3,泊松比為0.3,彈性模量為600 MPa,剪切模量為45 MPa。刀片材料采用65Mn,力學特性參數如下:密度為7 850 kg/m3,泊松比為0.3,彈性模量為2 060 MPa,剪切模量為80 000 MPa。
1.2 試驗模型
本研究將小麥莖稈抽象成連續、均勻的中空圓柱體理想化模型。經試驗測得小麥莖稈平均外直徑4.5 mm、平均內直徑3.5 mm、壁厚0.5 mm,取莖稈長100 mm。刀片為光刃直刀,單面磨刃,刀片刃角根據Chanceller的研究結果,設定為20°[9],刃口半徑設為0.02 mm,刀片厚度設為4 mm,所建立的幾何模型及網格劃分結果見圖1。
1.3 試驗因素及方法
影響莖稈切割的因素較多,本研究主要以切割速度、滑切角及削切角為試驗因素[10],因素水平根據設計經驗值上下浮動選取。分別在有限元軟件ANSYS的顯示動力學模塊Explicit Dynamics和離散元軟件EDEM中進行單因素仿真對比試驗,探討各因素對切割效果及峰值切割力的影響,并對比2種仿真方法的試驗結果,確定最佳參數,建立莖稈離散元模型。試驗因素水平設計如表1所示。
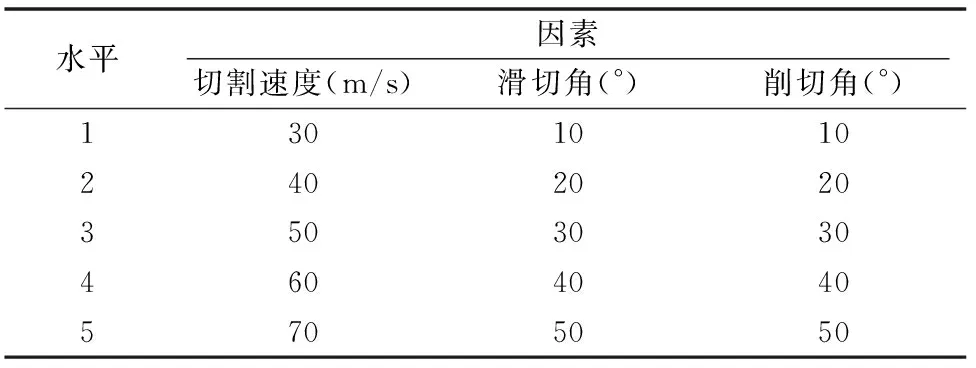
表1 試驗因素及水平
2 仿真對比試驗
2.1 有限元仿真結果分析
2.1.1 切割速度 刀片與小麥莖稈的切割形式為沖擊式無支撐正切(滑切角為0°,削切角為0°),無重力場,不對莖稈施加約束,切割速度為40 m/s的切割力曲線及不同切割速度峰值下的切割力分別見圖2和圖3。
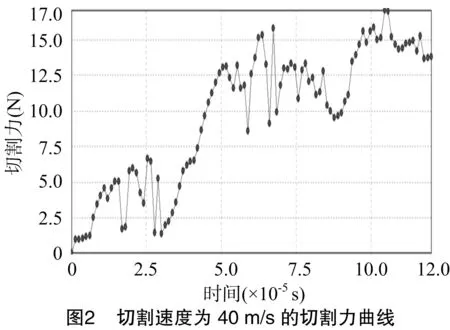

根據仿真結果,在沖擊式無支撐切割情況下,峰值切割力隨著切割速度的加快而增大,當切割速度達到60 m/s時,切割力會有1個階躍。雖然更大的切割速度能夠快速切斷莖稈,但是過大的峰值切割力會造成動力的浪費,而當速度低于 50 m/s 時,雖然能夠切斷莖稈,卻會伴有撕扯現象。因此,在試驗水平范圍內正切速度設為50 m/s左右較為合適,既能較好地切斷莖稈,并且適中的峰值切割力也不會造成動力的過度損耗。
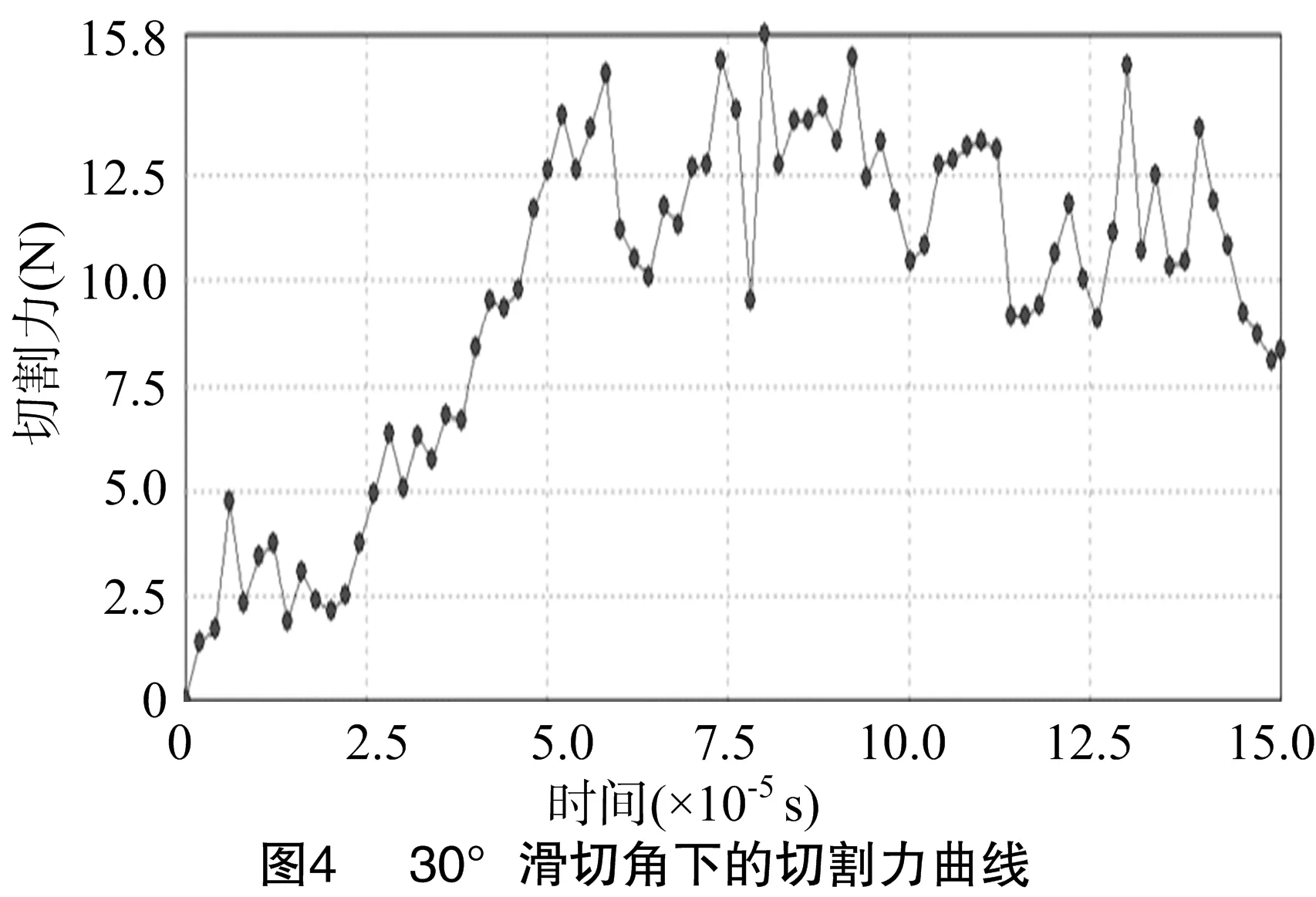
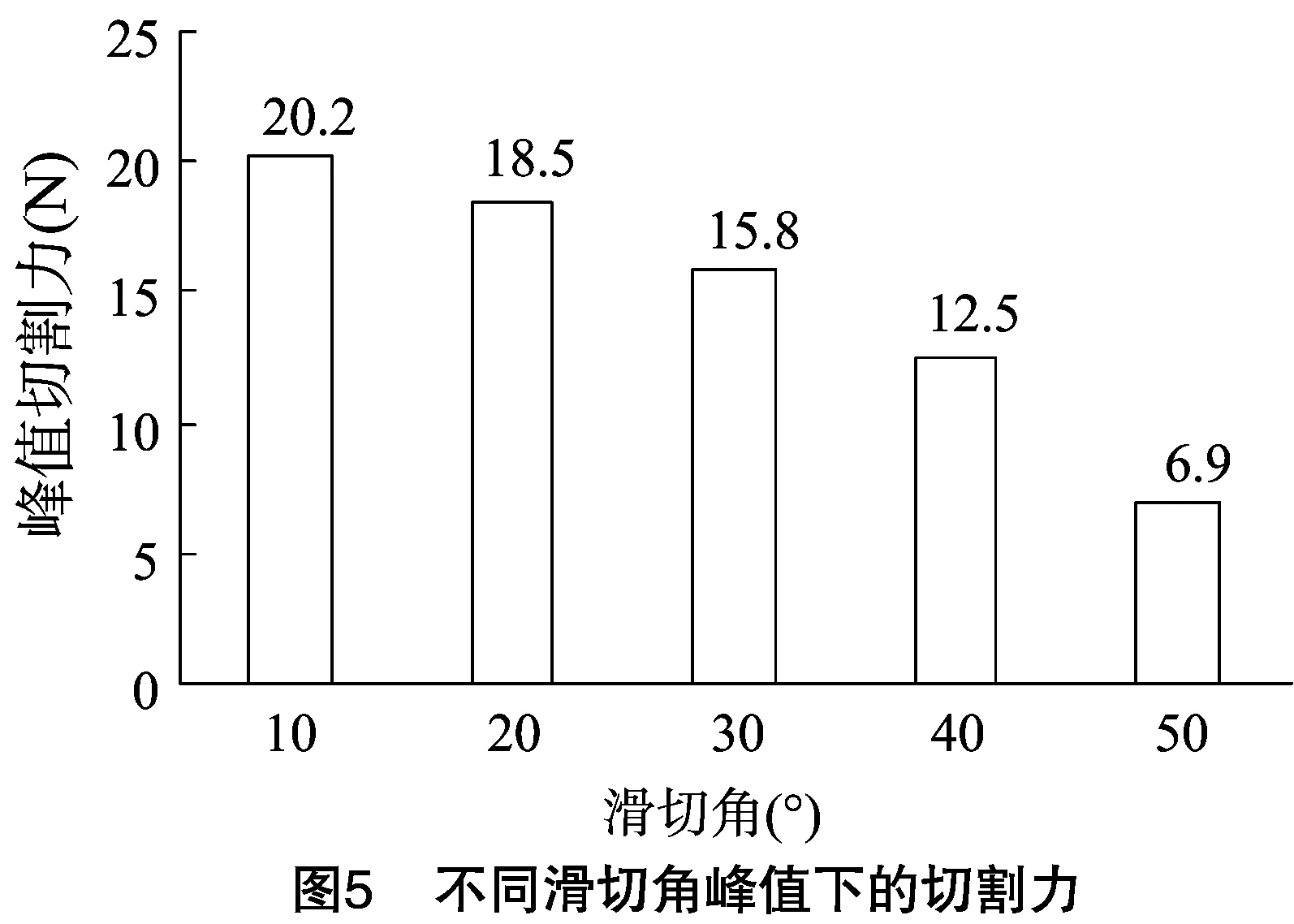
2.1.2 滑切角 滑切角即刀刃上任意一點的切割速度方向與該點處法向方向之間所形成的夾角,也是影響切割力的重要因素之一。設定切割速度為50 m/s,無重力場,不對莖稈施加約束。在滑切角為30°條件下的切割力變化曲線及不同滑切角峰值下的切割力分別見圖4和圖5。
由圖5可知,在30°滑切角下,刀片的峰值切割力為 15.8 N,而當速度為50 m/s的正切時,由圖3可知,刀片的峰值切割力為22.9 N。因此可見,在同等條件下,滑切比正切省力。隨著滑切角的增加,刀片所受的峰值切割力逐漸減小,滑切角在10°~40°區間時,峰值切割力呈現緩慢減小的趨勢,當滑切角達到50°時,峰值切割力有了較為明顯的下降。雖然較低的峰值切割力從動力節省角度來說更優,但是從仿真過程來看,滑切角過大,刀片切斷莖稈所需要的時間越長,效率也較低。因此,在試驗水平范圍內滑切角設為30°較為合理。
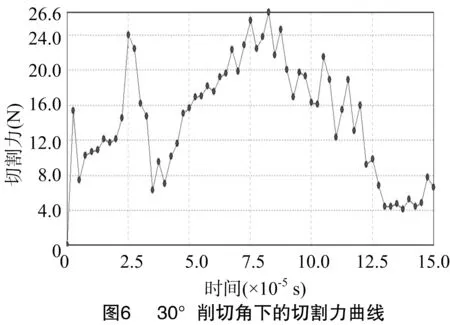
2.1.3 削切角 切碎裝置內的切割形式復雜多變,存在各種形式的切割,削切角即切割刀片的刀刃底面與莖稈橫截面所成夾角(取銳角)。設切割速度為50 m/s,無重力場,不對莖稈施加約束,滑切角為0°。圖6為30°削切角下刀片切割力的變化曲線。
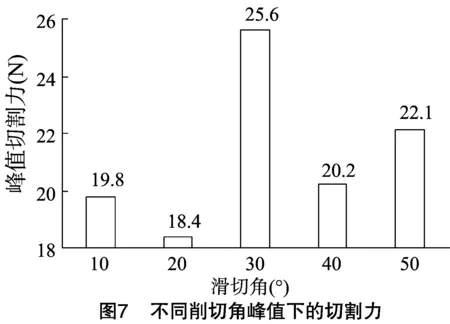
由圖7可知,當削切角為20°時,峰值切割力為18.4 N,而50 m/s切割速度正切的峰值切割力為22.9 N;當削切角為30°時,峰值切割力達到最大值25.6 N,超過了正切的峰值切割力(22.9 N)。在所選擇的削切角范圍內,峰值切割力沒有表現出特定的變化規律,不同削切角所得峰值切割力之間差異不大,對峰值切割力無明顯影響,且削切和正切的峰值切割力大小基本相同。
2.2 離散元仿真分析
有限元分析更加側重于分析物體的形變過程,適用于單根莖稈的切割受力分析,但是無法處理大量莖稈的群體切割模擬。而離散單元法把整個介質看成是由一系列離散的運動顆粒組成的,將各個單元的運動和位置變化綜合在一起來描述整個介質的變形和演化[11]。相關研究表明[12-14],在處理莖稈群體問題時,離散單元法將更有優勢。
2.2.1 莖稈離散元Bonding模型的建立 作為研究莖稈群體的基礎,需要取單根莖稈作為研究對象,建立基本的莖稈離散元模型。幾何模型仍然采用如圖1所示的中空圓柱體,在EDEM中設置莖稈材料屬性,并用球型顆粒對莖稈幾何模型進行填充,填充后的效果如圖8所示。

在EDEM中,Herts-Mindling with Bonding這一接觸模型可以用來黏結各個球型顆粒,形成可以連接2個顆粒的黏結鍵(bonding)鍵,該鍵可以承受切向及法向位移,當受到的外力達到設定最大法向和切向應力時,bonding鍵斷裂,顆粒間的黏結效果消失,即可以用來表征研究對象受到破壞。
在刀片切割莖稈的過程中,刀片的峰值切割力對應于來自莖稈表面對刀片的最大阻力。同樣的,顆粒間的bonding鍵也會對刀片產生阻力,并且會因為受力過大而發生斷裂現象。因此,以bonding鍵力來表征莖稈表面韌性,判斷峰值切割力的大小,是用離散單元法模擬分析莖稈切割的關鍵所在。
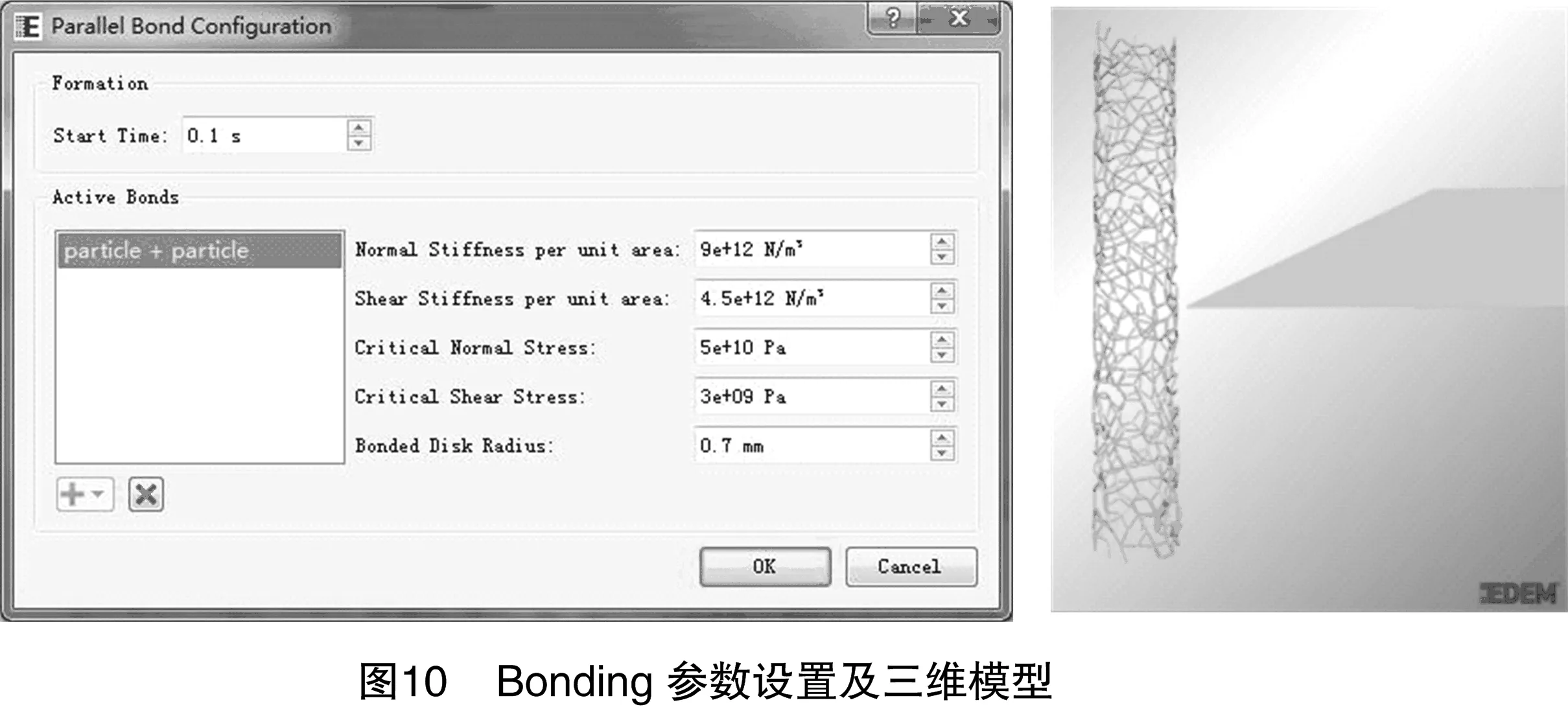
2.2.2 Bonding模型參數標定 在Herts-Mindling with Bonding接觸模型中,需要設置各項參數,這些參數決定了bonding鍵的屬性以及鍵力大小,即決定了各個球型顆粒之間能夠承受的最大法向和切向應力。由于目前該研究領域沒有相關資料可供參考,因此以“2.1.1”節利用有限元軟件ANSYS仿真模擬的峰值切割力為參照,在EDEM中對各參數進行虛擬試驗標定。
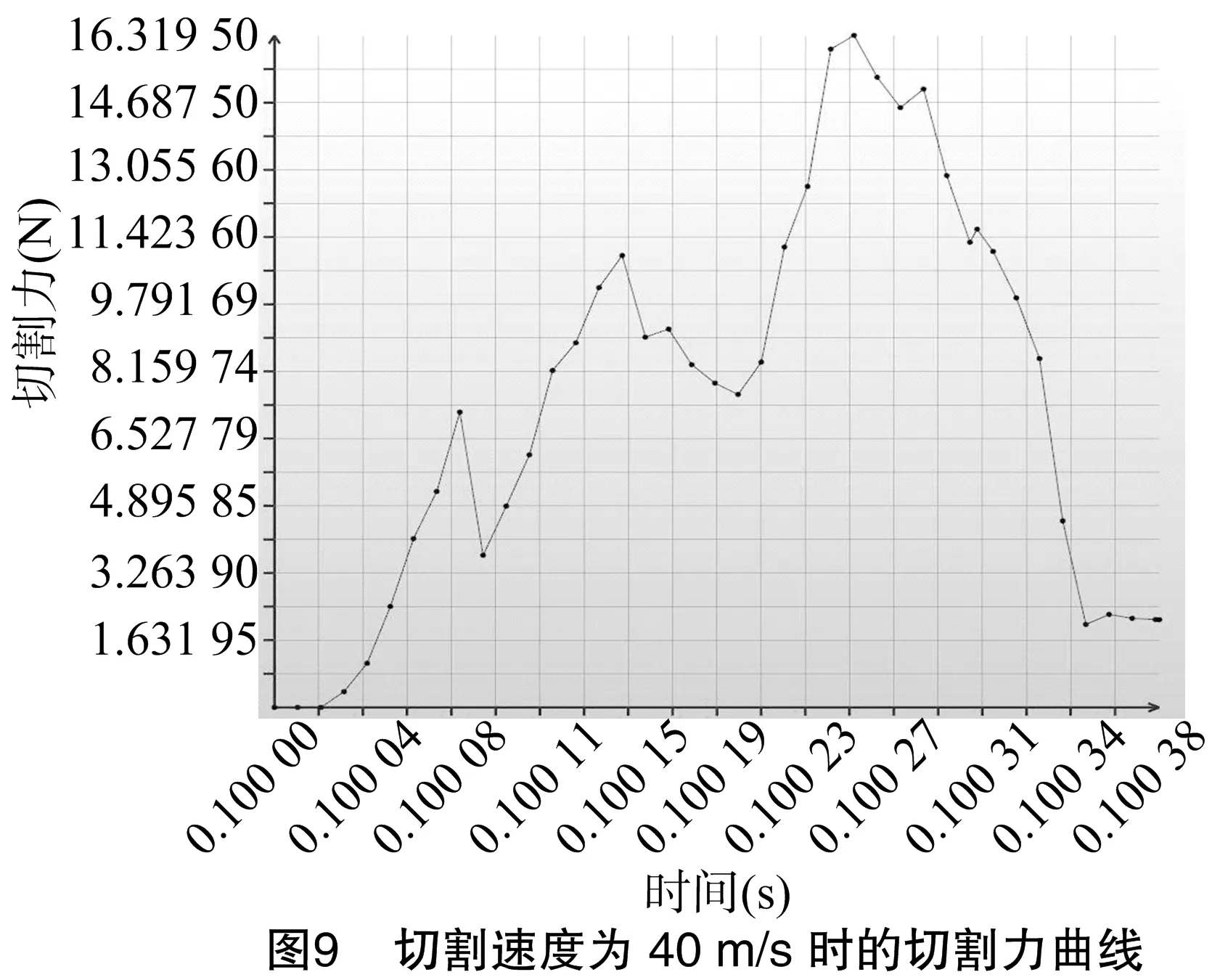
虛擬標定試驗所用刀片模型和ANSYS仿真試驗保持一致,切割形式仍然采用沖擊式無支撐正切。選取40 m/s的切割速度作為標定水平,在切斷莖稈后輸出峰值切割力進行對比,根據二者結果不斷調整bonding模型參數,以達到最接近的峰值切割力和切割效果,最終的峰值切割力為16.32 N,與ANSYS仿真結果相近,詳見圖9。Bonding模型參數及bonding三維模型見圖10。
2.2.3 不同切割速度仿真 以“2.2.2”節所得Bonding模型參數分別進行切割速度為50、60、70 m/s的沖擊式無支撐正切仿真,各個切割速度下的峰值切割力結果如圖11所示,其中50 m/s切割速度的峰值切割力為19.39 N,60 m/s切割速度的峰值切割力為33.51 N,70 m/s切割速度的峰值切割力為39.44 N。
由圖11可以看出,當切割速度為50~70 m/s時,刀片切割具有bonding鍵力的莖稈離散元模型,峰值切割力數值與有限元法分析的結果接近,平均誤差率約為8.6%。當切割速度逐漸增大時,峰值切割力的變化趨勢與階躍點也保持一致。
上述仿真試驗結果表明,利用Herts-Mindling with Bonding接觸模型來建立具有表面韌性的莖稈離散元模型是可行的,能夠體現莖稈在不同切割條件下被切斷時的峰值切割力,且所建立的莖稈模型可用于后續的莖稈群體仿真試驗。
3 結論
(1)切割質量隨切割速度增大而有所提升,峰值切割力也逐漸變大。峰值切割力隨削切角的變化沒有表現出明顯的規律,而隨滑切角的增大而減小,滑切角在50°時,峰值切割力明顯減小。在同等條件下,切割效果較好且省力的切割形式應為切割速度為50 m/s時的滑切。

(2)利用Herts-Mindling with Bonding接觸模型,根據有限元仿真結果標定的參數,建立了莖稈離散元模型并進行了不同速度的切割仿真。結果表明,刀片的峰值切割力與有限元仿真結果相近,在50、60、70 m/s切割速度下的峰值切割力平均誤差率約為8.6%,且峰值切割力隨切割速度的變化趨勢保持一致,表明所建立的模型較為準確。
(3)在模擬單莖稈切割時,基于離散單元法的仿真同有限元方法相比,所需時間大幅度減少,且結果相差不大,仿真效率更高。由于莖稈切割更注重的是動力的消耗和整體切割效果,在EDEM軟件中可以直觀地顯示刀軸的扭矩、功耗及最終的切割結果,并且能更好地體現群體受力以及運動狀態的改變。因此,采用離散單元法來模擬莖稈切割的過程將更合適。
(4)本研究探討的是以有限元仿真結果為基礎建立的莖稈離散元模型的可行性和準確性,后續可以該模型為基礎展開群體切割理論研究和仿真試驗,并為聯合收割機莖稈切碎裝置的結構設計改進提供一定的參考依據。

