“一題一課”中考專題復習
——“玩轉”兩個等邊三角形

王 燕 王 超

（1.山東省濱州市惠民縣李莊鎮中學 山東濱州 251712；2.山東省濱州市濱城區第六中學 山東濱州 256600）

中考把關試題往往都是經過充分的打磨、苦心經營而推出的，既承擔了必要的選拔區分功能，又傳遞著教學導向，值得老師們認真思考，在貫通思路、洞察問題結構之后，還可將考題設計成習題課，開發成“一題一課”，引導學生深入思考。本文選取2015年山東濱州一道把關題，簡述求解思路之后，給出該題的習題解題教學設計，拋磚引玉，供研討。

教學目標：

1.復習等邊三角形的性質及判定，平行線的性質及判定，全等三角形的判定及性質，相似三角形的性質及判定等知識。

2.能熟練應用性質及判定靈活的解決問題。

3.結合知識點，能形成知識網絡，達到能掌握知識間的內涵和外延，提升復習的高度。

教學重點：復習三角形全等、相似的性質和判定及其運用

教學難點：知識網絡的形成，提高數學內容的復習水平和復習效率

教學過程：

一、每日一題

如圖，已知B、C、E三點在同一條直線上，△ABC與△DCE都是等邊三角形，其中線段BD交AC于點G，線段AE交CD于點F，

求證：（1）△ACE≌△BCD；

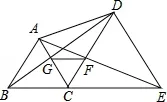
生上臺講解解題思路，師適時的點撥。

設計意圖：由于等邊三角形是特殊的三角形，在多個地方，多次考查與等邊三角形有關的題目，以上每日一題是2015年濱州中考題第23題，它就是以等邊三角形為載體，考查與其相關的一些幾何知識。借此中考題我們深入的探究一下與其相關的內容。

二、問題探究

活動一：作圖體驗

例 點C是線段AB上的動點（C點不與A、B重合），分別以AC、BC為邊在直線AB的同側作等邊三角形ACD和等邊三角形BCE，AE與CD相交于點M，BD與CE相交于點P.

師：請同學們根據題意，畫出圖形。

生：在練習本上作圖，師板演畫圖。

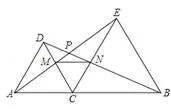
設計意圖：為了讓同學們在作圖過程中，能清晰的觀察，體會復雜圖形的形成過程，能在復雜圖形中分離出基本的圖形，容易觀察出平行線，相似三角形等，為解決后面的探究問題做好鋪墊。

活動二：問題探究，層層遞進

探究1.根據已知條件，你能從圖中共找出幾對全等的三角形？

設計意圖：復習等邊三角形的性質和全等的判定方法，發散學生思維，類比證明三角形全等的方法，達到融會貫通。

探究2.圖中除了已知兩個等邊三角形的內角是60度，還有哪些角為60度？

設計意圖：探究等邊三角形，復習等邊三角形的判定方法，證明∠DPA=∠EPB=60°，并為后面的斜8字圖三角形相似和圖形變換——旋轉的性質做鋪墊。

探究3.圖中有幾組平行線？

設計意圖：結合每日一題一組平行，及畫圖過程中的平行線總結3組平行線，復習平行線的判定方法。

說明：前三個探究為了說明等角，等線常用的證明方法和作用。

探究4.根據前面得出來的結論，你能找出圖中相似的三角形嗎？

設計意圖：根據平行線判定三角形相似，進而一一復習三角形相似的判定方法，歸納出三角形相似的基本常見模型：“A”字型，“8”字型，“一線三等角”等常見模型的問題。

師：講解分析，并板書：相似三角形的常見模型

探究5.你能證明MN2=EN·DM嗎？

設計意圖：三角形相似性質的延續，要想證明等積式，需要先化成比例式，尋找三角形相似，進而承接上面的探究。有助于學生逆向思維的形成，讓學生學會綜合分析法證明幾何問題。

活動三：深入探究 思維升華

探究6.若AB=10，設AC=x，MN=y，那么你能表示出y與x的關系嗎？當x為多少時，y有最值？

設計意圖：三角形相似的性質對應邊成比例，可得出線段的等量關系，因此可構建關系式，

若是存在兩個變量，則可以構建函數解析式，進而解決問題。由此也實現的代數與幾何的鏈接，將幾何問題升華為函數問題。

追問：探究6若改成下面的問題，解答和上面的探究6有區別嗎？

變式：若AB=10，當點C在AB上動時，是否存在一個位置，使得MN的長最大？若存在，求出這個點C的位置，若不存在，請說明理由。

設計意圖：變式問法，是為了讓學生接觸，在沒有變量的前提下，需要自己設出變量，自己搭建橋梁，構建出關系式解決問題，需要學生注意變量的取值范圍，要求學生有嚴密的思維。

三、課堂總結

1.學生總結出反思的問題，根據課堂所學，思考并畫出知識網絡圖，老師點撥。

2.學生嘗試總結課堂中用到的數學思想方法。

設計意圖：老師點撥構建網絡，引導學生把零散的知識捆扎，提升復習的高度，點撥學生總結的思想方法，以待遇到此類問題，以相關的思想方法解決這一類問題。進而達到提升中考專題復習的效果。

教后的幾點思考：

1.鋪墊問題，基礎出發，漸次生長

“一題一課”的教學設計，開課階段一定要平緩起步，堅持從基礎出發，讓更多的學生參與到初始問題的思考中來，能否更大范圍地調動所有學生的思維是這種課型的實施關鍵.基礎問題的設計又要服務于后續問題，即讓這些基礎題練習之后有助于思考后面漸次生長出來的能力題、提高題、拓展題，這就需要教師設計時充分關注后續問題的生長.

2.增設條件，靠近考題，啟發思考

在基礎題引導更多學生參與之后，就可陸續增設條件，靠近原來考題漸次增加強化條件，也不宜全盤托出，需要有必要的鋪墊，保持基礎偏弱學生探究的興趣和信心。因此在思維障礙點、解題難點處，教師可以通過必要的追問，或讓一些優秀學生重復講解他們是如何突破問題的關鍵點、難點的，也有助于讓更多的學生理解、貫通思路。

3.重視提煉，滲透數學的思想方法.

在復習課教學中，教師要及時引導學生進行提煉，提煉數學知識、思想方法、解題策略，挖掘動態問題中不變的量，同時要滲透各種數學思想方法。通過提煉、滲透，讓學生能夠從中理解知識點的內涵和外延，從反思過程中汲取經驗教訓，鞏固和擴大解題成果，進一步提升學生思維的深刻性.