基于Sigmoid函數的S型加減速控制方法研究*
方佳偉,蔡錦達,姚 瑩,張大偉
(1.上海理工大學 機械工程學院,上海 200093;2.上海理工大學 出版印刷與藝術設計學院,上海 200093;3.上海理工大學 教育部光學儀器與系統工程中心,上海 200093)
0 引 言
為減小機械設備在啟停階段的沖擊、失步、超程或振蕩,必須設計專門的加減速控制規律,使加給電機的輸入(脈沖頻率或電壓)按照這個規律變化,從而使設備在各種工況下都能快速、準確地停留在給定的位置上(這種控制稱為加減速控制)。
目前S型加減速控制方法已經被廣泛應用于實際工程當中。文獻[1]提出了基于位移的7段加減速方法,這種方法通過位移求解速度,通過多項式擬合生成S型曲線,運算量大,設備加減速階段沖擊時間長。
本文將提出基于Sigmoid函數的S型加減速控制方法,從位移、速度、加速度以及加加速度等方面論證該控制方法的可行性;采用非等時離散化的時間規劃方法對加減速的時間分段做優化與改進;采用時間與速度數組遍歷查詢的方法進行程序設計;通過基于ARM9微控制器的龍門式點樣儀進行實驗,利用激光跟蹤儀進行測量,以驗證基于Sigmoid函數的S型加減速控制方法的有效性。
1 基于Sigmoid函數的S型加減速控制方法
設備在啟停階段若未使用加減速,會產生明顯的抖動,對精度造成影響。所以在設備啟停階段必須使用加減速來減小抖動。常見的加減速曲線有直線型加減速、指數型加減速和S型加減速[2]。龍門式點樣儀使用S型加減速控制方法來減小啟停階段的抖動。
1.1 控制方法的模型分析
典型的S型加減速控制方法,大多使用多項式函數或者分段函數,函數的表達式為構造函數,完成S型的擬合,Sigmoid函數本身就為平滑的S型曲線,表達式為:
(1)
式中:S—Sigmoid函數應變量;x—Sigmoid函數自變量。
由于Sigmoid函數關于(0,0.5)中心對稱,而時間為非負數,所以將式(1)中的x用時間t-0.5n替換,S用速度v替換,那么式(1)就轉換為速度-時間的函數:
(2)
式中:v—設備運動速度;t—設備運動時間;n—加速階段或者減速階段完成的時間周期數。
式(2)中,為了使得設備在最短的時間內,零點處減小階躍信號的影響,并且保證步進電機不出現抱死現象(頻率小于250 Hz),保證加減速末端線性度(斜率小于0.005),則須滿足:
(3)
式中:v—設備運動速度;t—設備運動時間;n—加速階段或者減速階段完成的時間周期數。
通過式(3)可以求得n=6。將式(2)積分可以得到位移d關于時間t的函數式:
d(t)=ln(et-6+1)
(4)
式中:d—設備運動距離;t—設備運動時間。
將式(2)求一階導數和二階導數分別可以得到加速度a和加加速度j關于時間t的函數式:
(5)
式中:a—設備運動加速度;t—設備運動時間。
(6)
式中:j—設備運動加加速度;t—設備運動時間。
式(3~6)的函數圖像如圖1所示。
通過幾何法得出,圖1(a)中S型曲線未使用分段函數進行擬合,直接通過超越函數即可得到S型的曲線。
圖1(b)位移-時間圖像末端取點可得:
當t-6>3 ms時,距離-時間公式可近似為:
d(t)=k·t
(7)
式中:d—設備的運動距離;k—勻速運動時的速度;t—設備運動時間。
式(7)證明了該加減速控制方法的末端線性度好,能夠平滑地從加速階段過渡到勻速階段。
通過幾何法分析圖1(c)加速度-時間圖像可以得出當t-6=0時,加速度達到最大值,即加速度的最大值為:
amax=0.25·m
(8)
式中:amax—加速度最大值;m—達到勻速狀態之前,加速度的最大設定值。
式(8)中表示當m的值取值越大,加速階段加速度越大,會產生步進電機抱死現象[3],后文中通過時間分段的非等時離散化設計解決該問題[4]。
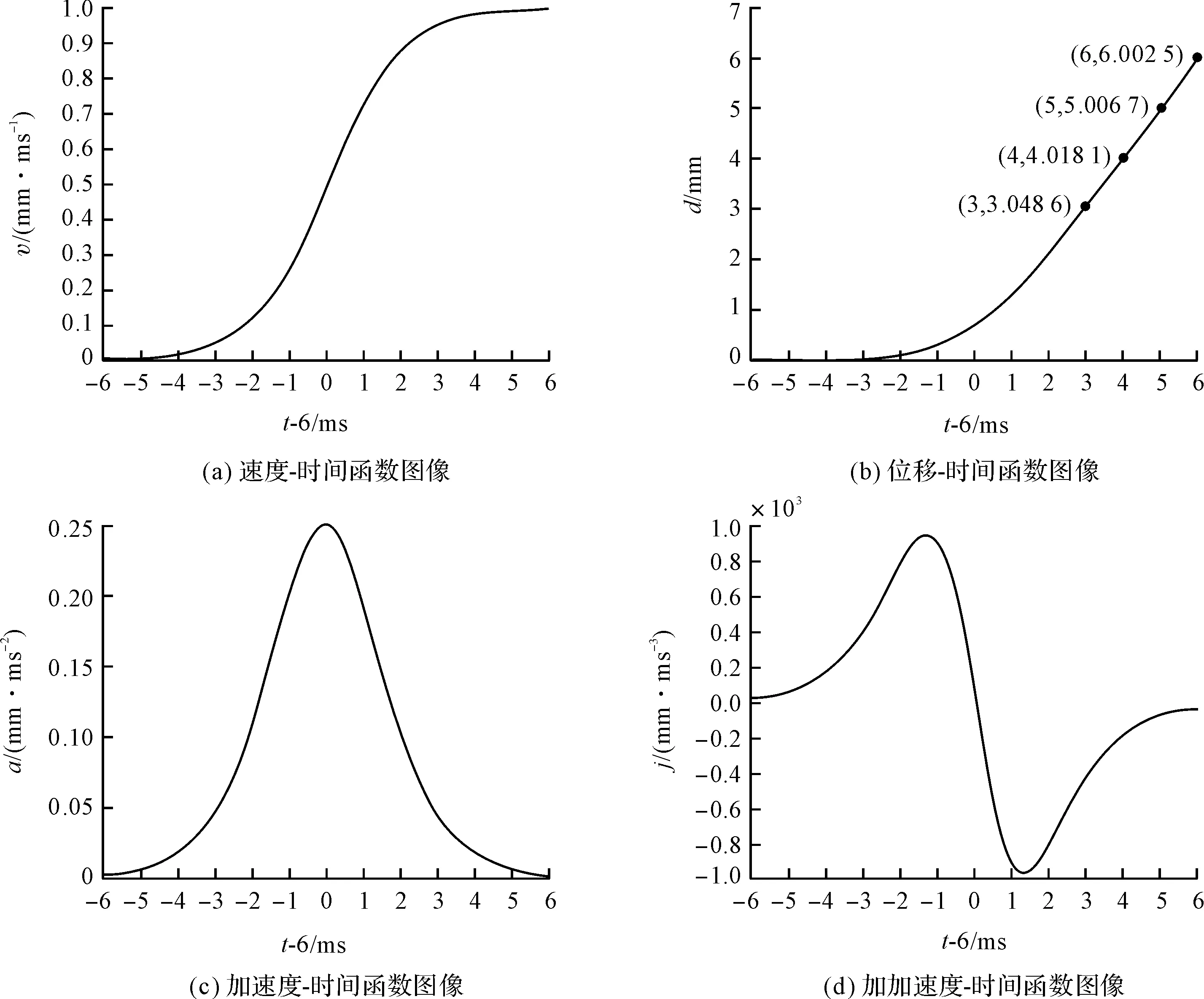
圖1 基于Sigmoid函數的S型加減速控制方法的函數圖像
通過解析法,對式(6)求導可得:
(9)
式中:j—設備運動加加速度;t—設備運動時間。
加加速度的最大值反應了系統的柔性,值越大,則沖擊越大;值越小,則加減速時間長[5]。文獻[6]中7段加減速的控制方法加速階段的速度-時間公式:
(10)
式中:v—速度;vs—初速度;j′—加加速度;0~t1,t2~t3—加速階段中加速度變化的階段;t1~t2—加速階段加速度不變的階段。
式(10)中,在兩種加減速控制方法的加減速時間相同(t=12 ms)的情況下設:vs=0,v4=1 mm/ms,可得:
當t2-t1<1.065 ms時,j′>jmax
式(10)中,在兩種加減速控制方法的最大加加速度相同(j′=jmax=0.096 32 mm/ms2)的情況下設:vs=0,v4=1 mm/ms,t2-t1=0,可得:
(t1+t2+t3)min=6.444 ms
由上結論可知:當7段加減速控制方法與基于Sigmoid型S型加減速控制方法的加減速時間相同時,7段加減速的勻加速階段時間必須小于整體時間的1/12。當7段加減速控制方法與基于Sigmoid型S型加減速控制方法的加加速度最大值相同時,7段加減速的時間短,但7段加減速的加加速度為定值,所以沖擊值為常量,對精度影響大。Sigmoid型加減速的最大沖擊值為瞬態值,對精度影響小。減速階段與加速階段對稱。
1.2 控制方法的時間分段規劃
通過幾何法將圖1(a)等時離散化以及非等時離散化后,如圖2所示。
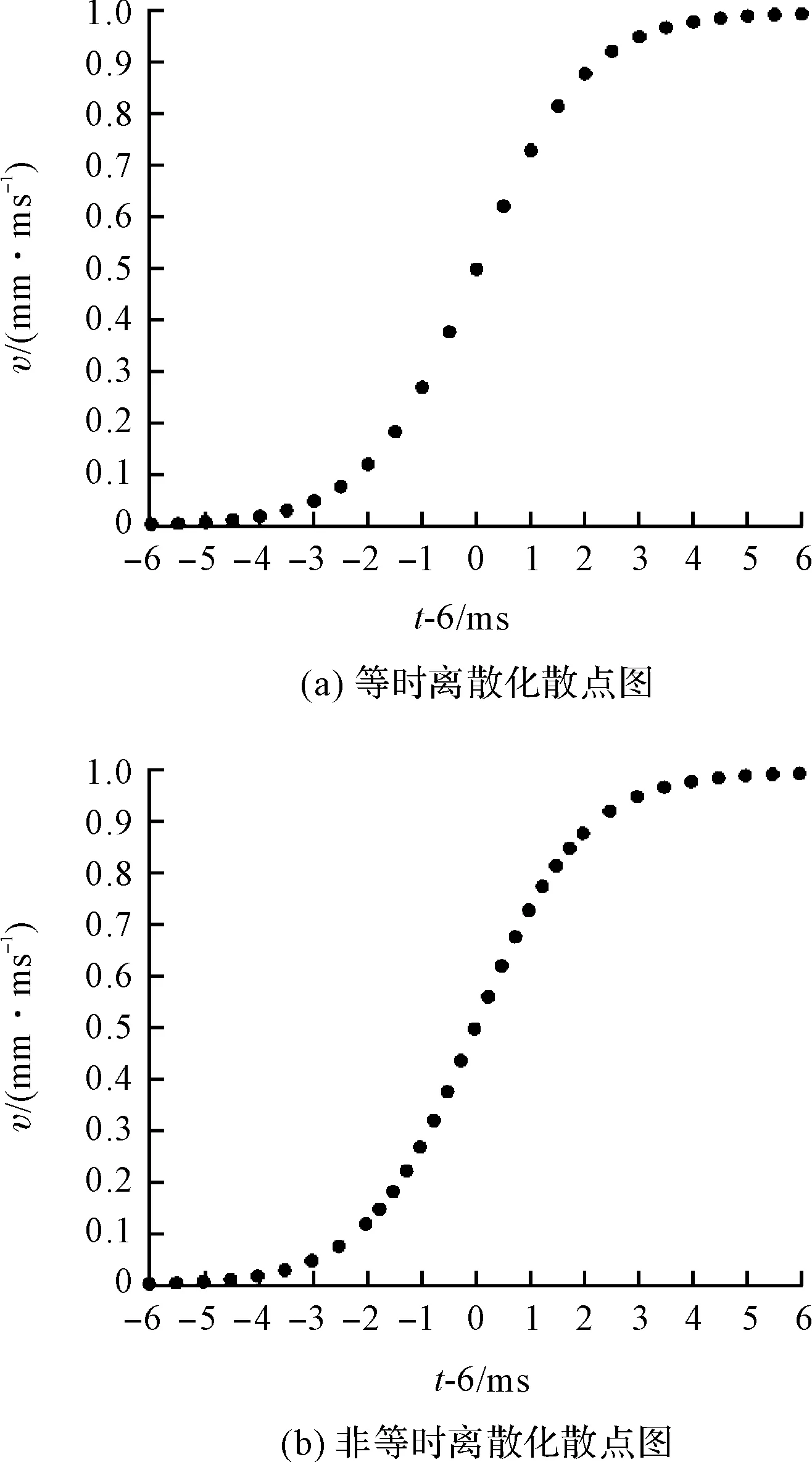
圖2 基于Sigmoid函數的S型加減速的時間離散化散點圖
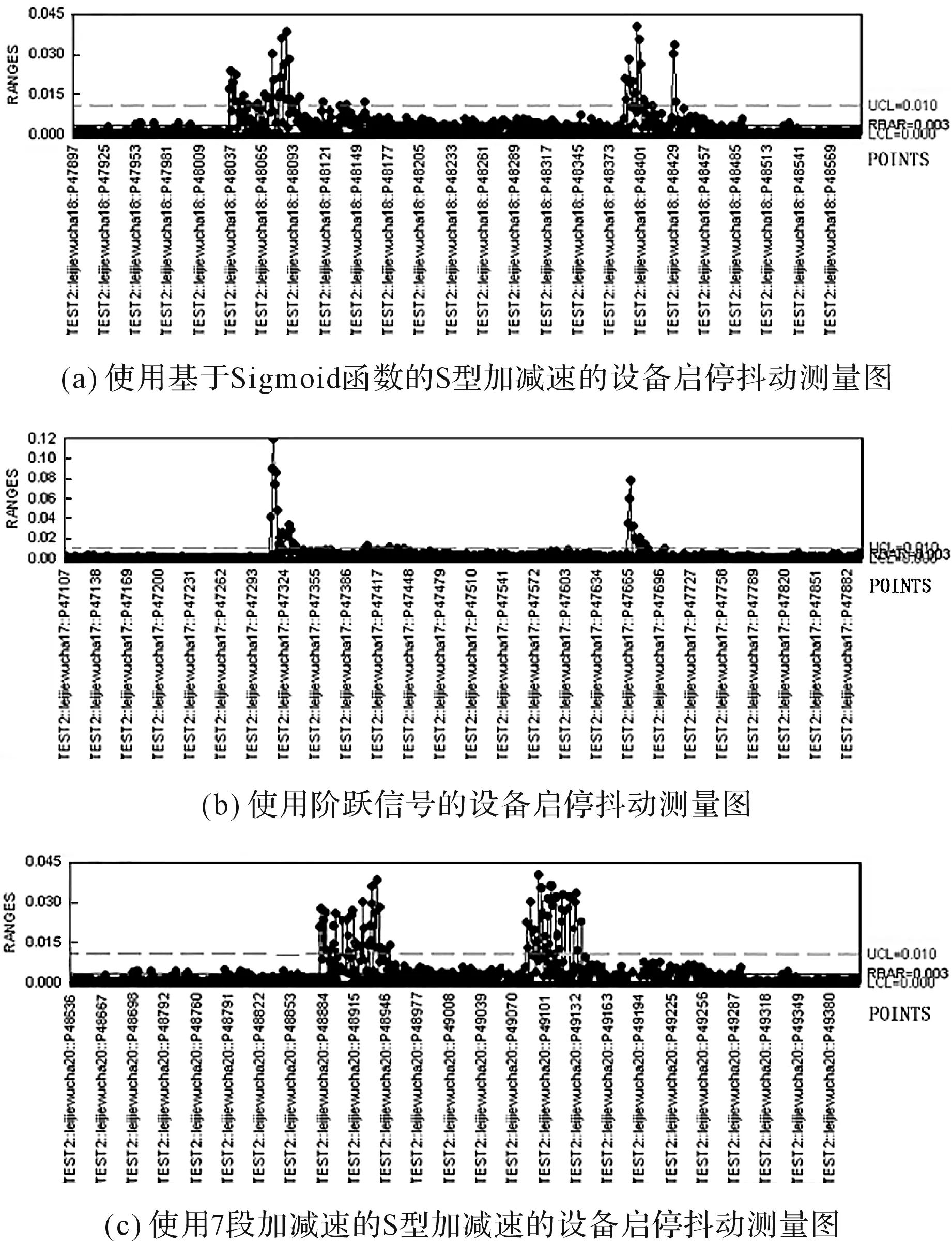
通過幾何法可知圖2(a)中,當-2 (11) 式中:T—等分時間段;t—設備運動時間;k1,k2—非等時分段系數。 式(11)中,根據需要選擇:k1=0.5,k2=0.25,其結果如圖2(b)所示。 通過圖2(a)和圖2(b)的對比,可以得出:非等時離散化方法相比于等時離散化所得到的時間分段,將時間分段從原先的12段等分時間段轉換成了16段非等分時間段,使得Δv/Δt的最大值減小,運動更加平穩。 綜合上述分析可知,對于ARM9嵌入式微控制器的程序設計主要過程是根據外部傳入的速度參數以及時間參數計算出步進電機所需要的頻率以及改變頻率的時間點[7]。 根據圖2可知速度參數和時間參數的數量較多,為了提高程序的執行效率,本研究采用數組查詢的方式設計程序[8]。 必須先建立時間數組才能夠通過時間數組建立速度數組。根據外部傳參分段數n、加速時間T、非等時分段系數k1,k2,通過圖2(b)以及式(11)可以設計出求時間數組time[n]的流程圖,如圖3所示。 圖3 時間數組規劃流程圖 通過圖3計算得出時間數組之后,可以迅速遍歷數組得到數組中的值進行判斷以及運算。 步進電機由脈沖信號進行控制的,ARM9嵌入式微控制器有兩種脈沖控制模式,一種是通過PWM生成波形,另一種是通過對GPIO的控制輸出波形[9]。兩種方式的原理均為重載定時器中TCNT寄存器的值來改變脈沖的頻率以獲得所需步進電機的轉速[10]。根據外部傳參速度V以及2.1節求解出的時間數組,求解出速度數組v[n],并通過ARM9控制器的脈沖生成原理設計整體控制流程,如圖4所示。 圖4 速度數組建立及控制流程圖 基于Sigmoid函數的S型加減速控制方法是超越函數,非普通多項式函數,計算成本高,無法在運動的同時計算所需數值,所以必須事先完成相關數值計算。在計算機中,通過數組形式對數值進行存放、遍歷,此種方法速度快、效率高,是一種高效的S型加減速處理方法[11-12]。如圖4所示,基于Sigmoid函數的S型加減速控制方法的時間離散化可通過Timer1定時器的定時時間time1確定,脈沖發生的頻率通過Timer2定時器TCNT2進行重裝載。其減速階段與加速階段對稱。 本文使用龍門式生物芯片點樣儀作為實驗設備。生物芯片對于點樣精度的要求高,所以生物芯片的生產設備在精度上要優于普通設備,且步進電機啟停階段的抖動會影響設備精度[13]。因此本研究利用激光跟蹤儀對設備啟停階段的抖動進行測量,驗證基于Sigmoid函數的S型加減速控制方法的有效性。 龍門式點樣儀的機械系統主要由點樣儀機械平臺、點樣基質工作平臺組成,如圖5所示。 圖5 龍門式點樣儀裝置 圖5中龍門式點樣儀機械平臺采用托盤固定的龍門式直角坐標結構。X軸的兩根支撐導軌設計在龍門的兩側,X軸滑塊在兩根導軌上作直線運動,Y軸滑塊沿龍門方向作Y向運動,點樣儀的點樣噴頭模塊固定在Z軸上,可以在X-Y平面內運動,也能在Z軸方向上實現升降。這種方案以剛度、強度都較大的兩側固定支撐導軌作為連接兩個運動機構的橋梁,將點樣工作區域置于X向兩根支撐導軌之間,既能保障機械結構的剛度、精度和速度,又合理利用空間。由于托盤固定不動,芯片基質不會發生移動影響點樣精度。 本研究利用API T3激光跟蹤儀對實驗設備精度進行測量。激光跟蹤儀可以在短時間內采集多個樣點進行誤差分析。 本文對龍門式點樣儀使用基于Sigmoid函數的S型加減速控制方法的運動控制與使用階躍信號的控制方法、使用7段加減速控制方法進行對比實驗,其實驗結果如圖6所示。 圖6 實驗結果 圖6(a)中采用了基于Sigmoid函數的加減速控制算法之后,啟停動階段產生最大跟蹤誤差小于0.045 mm,持續的時間短。運動開始時,由于在加速或減速階段的加加速度的絕對值有兩處最大處,測量結果在加減速階段各出現兩個跟蹤誤差峰值。 圖6(b)中可得:使用階躍信號控制算法時,啟動階段速度突變大,加速度以及加加速度大,產生0.12 mm的跟蹤誤差,持續的時間短。 圖6(c)中可得:使用7段加減速控制算法時,啟停動階段產生最大跟蹤誤差小于0.045 mm,持續時間長。 由于激光測量儀動態跟蹤性能好,其跟蹤誤差可作為判別設備啟停階段抖動的依據。 實驗結果表明:使用基于Sigmoid函數的S型加減速控制方法,利用激光跟蹤儀采集的點的抖動均小于0.045 mm并且持續的時間短;使用階躍信號控制方法的抖動的最大為0.12 mm,持續時間短;使用7段加減速控制方法的抖動均小于0.045 mm,持續時間長。所以基于Sigmoid函數的加減速控制方法相比于階躍信號的控制方法可降低設備啟停階段62.5%的抖動,基于Sigmoid函數的加減速控制方法相比于7段加減速控制方法可降低設備啟停階段33.3%的抖動時間。 本研究提出了基于Sigmoid函數的S型加減速控制方法,并分析了該控制方法的位移、速度、加速度以及加加速度與時間的關系,論證了該控制方法的可行性;對加減速的時間分段方法做了優化與改進,論證了非等時離散化的時間規劃方法的有效性,并采用時間與速度數組遍歷查詢的方法進行程序設計;通過基于ARM9微控制器的龍門式點樣儀進行了實驗,利用激光跟蹤儀進行了測量。 實驗結果表明:基于Sigmoid函數的S型加減速控制方法要優于階躍信號的控制方法以及7段加減速控制方法,這為以后的研究提供了重要參考依據。2 S型加減速的程序設計
2.1 時間數組的建立
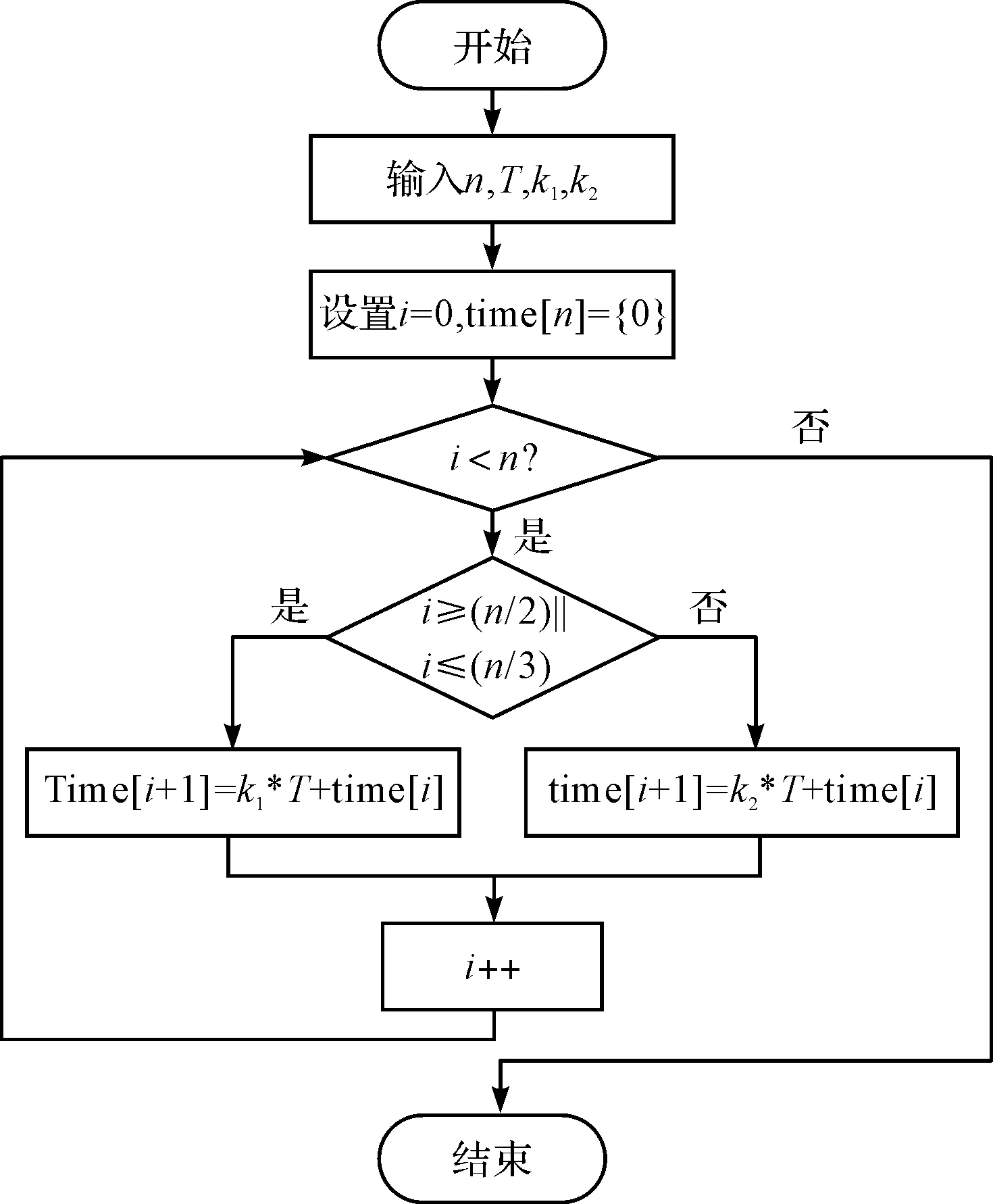
2.2 速度數組的建立與運動控制流程

3 實驗及結果分析
3.1 實驗設備
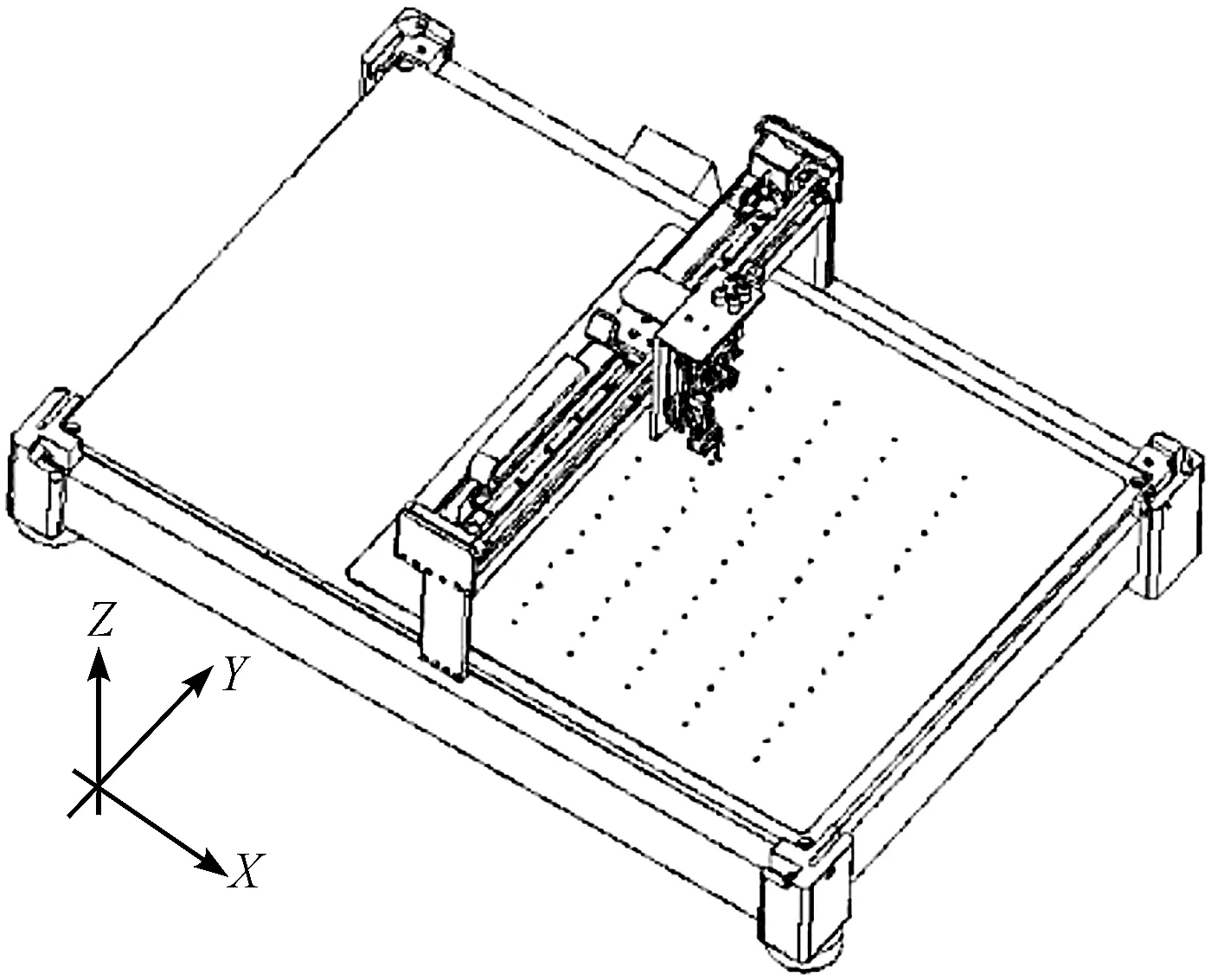
3.2 實驗結果分析
4 結束語

