基于動力學的擬人肩關節動載協調分配優化研究*

王 林，李研彪*，孫 鵬，羅怡沁，徐夢茹，鄭 航

(1.浙江工業大學 機械工程學院，浙江 杭州 310032；2.浙江工業大學 特種裝備制造與先進加工技術教育部重點實驗室，浙江 杭州 310032)

0 引 言

并聯機構具有結構緊湊、承載能力強、運動慣性小等優點，故廣泛應用于各種擬人關節[1-6]。由于并聯機構的動力學方程是非線性多輸入多輸出系統，存在多種分配組合來實現運動[7-10]。在穩定外載荷作用下，合理地優化分配各驅動可以有效降低能耗、減少驅動力。

目前，主要從驅動力矩最優和能耗最優兩個角度來進行動載協調分配，通過構建力矩分配模型和能量分配模型來實現優化[11-15]。其中，分配方式有加權最小二乘法、規劃載荷分配系數等。但上述優化方法均屬于單目標優化，只考慮驅動力矩或者能耗，且均從瞬時狀態考慮，未衡量機構的整個運動過程。因此，優化結果可能存在驅動力矩、速度等方面的波動或突變，這種波動、突變現象不利于機構的穩定運行。同時，只考慮力矩和能耗最小，也可能出現機構的運動時間較長，不利于提高機構的運動效率。

針對上述動載協調分配優化的不足，本文將考慮機構性能、時間、能耗和力矩波動4個因素，提出一種動載協調分配優化方法，并基于動力學模型，定義綜合性能指標，采用Dijkstra算法優化求解性能最優軌跡，最后用遺傳算法求解得到最優廣義時間。

1 肩關節機構的運動學分析

本文研究的肩關節機構以球面5R并聯機構為原型，肩關節的模型圖如圖1所示。

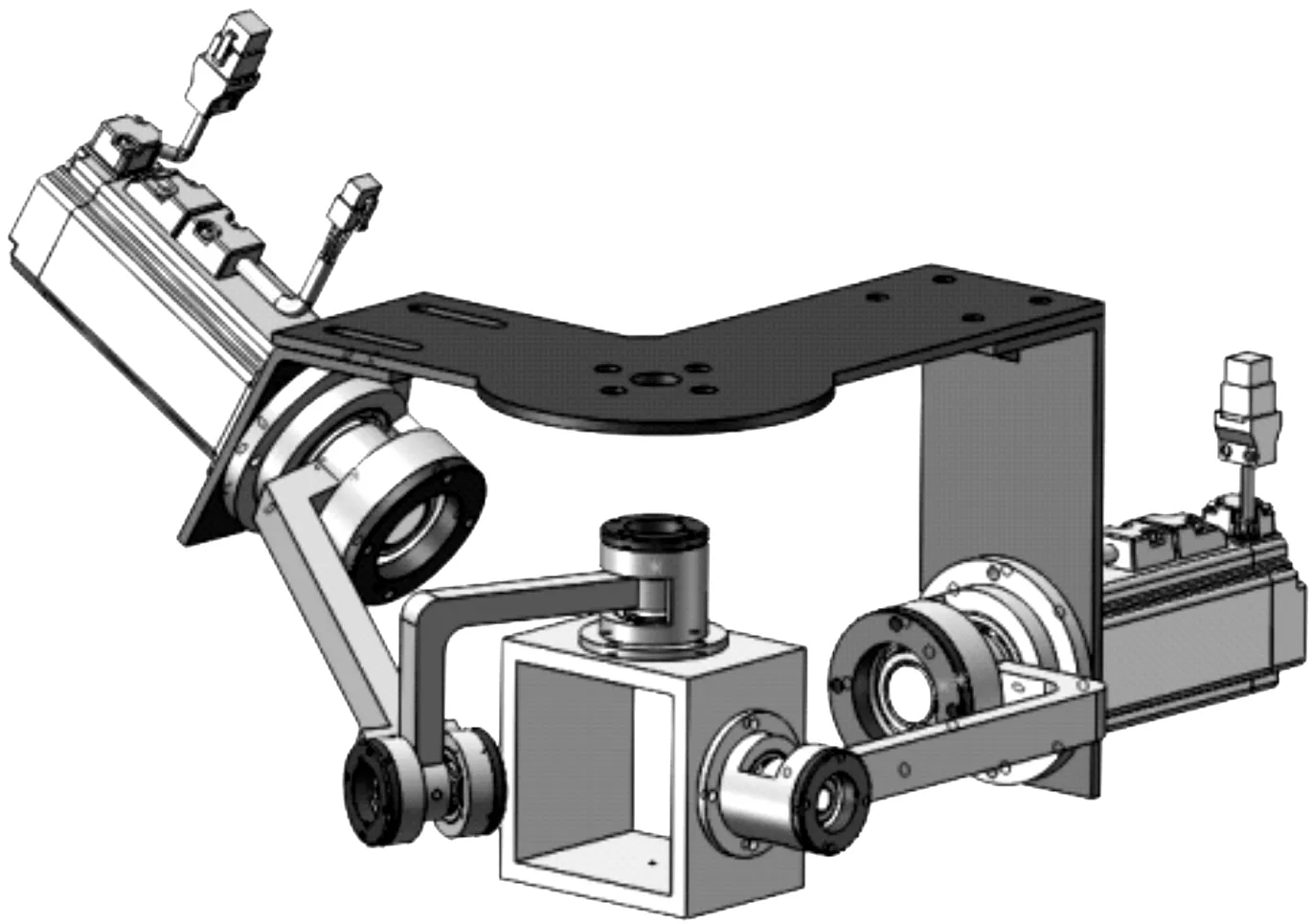
圖1 肩關節的模型圖

該機構由定平臺、動平臺和連接兩者的二條支鏈組成。運動副均為回轉副，且各軸線匯交于O點。其中，軸線OB1與軸線OC1、軸線OA2與軸線OC2、軸線OC1與軸線OC2相互垂直。

肩關節的機構簡圖如圖2所示。

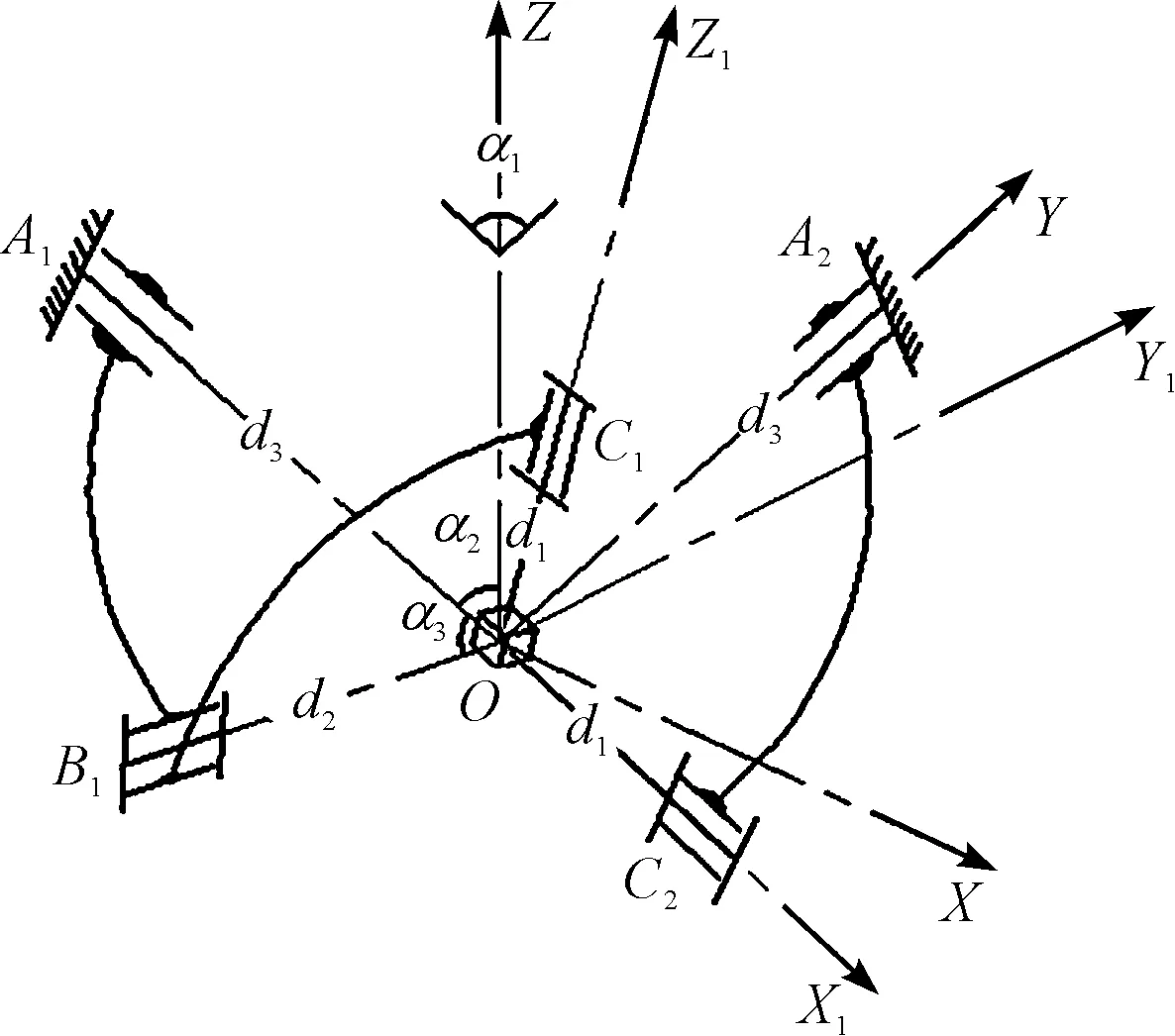
圖2 肩關節的機構簡圖α1—平面A1OZ和平面A2OZ所在平面的夾角，α1=90°；α2—Z軸與軸線OA1的夾角，α2=60°；α3—軸線OA1與軸線OB1的夾角，α3=70°；d1—回轉副C1、C2與機構中心O點的距離，d1=70 mm；d2—回轉副B1與機構中心O點的距離，d2=90 mm；d2—回轉副A1、A2與機構中心O點的距離，d2=185 mm

本研究建立定坐標系{O-XYZ}原點與機構中心O重合，Z軸沿OC1軸線方向，Y軸沿OA2軸線方向，X軸滿足右手螺旋定則。建立動坐標系{O-X1Y1Z1}原點與機構中心O重合，Z1軸沿OC1軸線方向，X1軸沿OC2軸線方向，Y1軸滿足右手螺旋定則。當定坐標系和動坐標系重合時，該機構處于初始位姿。

本研究采用Z-Y-X型的歐拉角描述動平臺的姿態，動平臺繞Z1軸旋轉角度為α，繞Y1軸旋轉角度為β，繞X1軸旋轉角度為γ，其中α=0 rad。關節驅動器1輸入角度為θ1，關節驅動器2輸入角度為θ2。

本研究根據肩關節機構的幾何關系，建立矢量約束方程，化簡可得位置反解：

(1)

式中：

其中，cαi=cosai，sai=sinai，(i=1,2,3)。

將式(1)兩邊對于時間t求導，速度反解可得：

(2)

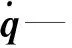
2 肩關節機構的動力學分析

為了便于建立動力學模型，本研究將肩關節機構的各連桿和動平臺均視為剛體，同時忽略各運動副之間的摩擦力和軸類零件的回轉運動。考慮慣性力、外力作用，建立肩關節機構的動力學模型。

2.1 慣性力分析

本研究采用拉格朗日方程計算肩關節機構的慣性力，將系統慣性力轉換到廣義歐拉坐標q=[γβ]T上。其計算過程如下：

肩關節機構的動能E包括E1和E2(其中：E1—平臺的動能；E2—各連桿的動能)。

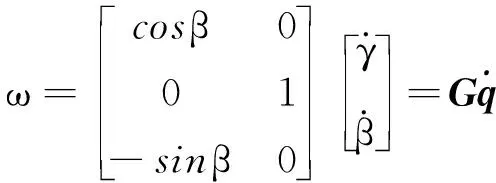
(3)

Ip表示過質心坐標系的轉動慣量矩陣，即：

Ip=RIHRT

(4)

式中：R—動平臺歐拉角所對應的旋轉矩陣。

綜合式(3,4)，可得動能E1:

(5)

動能E2的求解如下：

(6)

式中：I1—連桿A1B1的轉動慣量；I2—連桿A2C2的轉動慣量；I3—連桿B1C1的轉動慣量。

則肩關節機構的動能為：

(7)

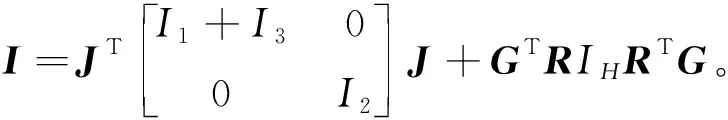
設定坐標系中OXY面為重力零勢能面，由于動平臺的質心與機構中心O點重合，且動平臺始終繞質心旋轉，動平臺勢能變化為零。則機構的總勢能V為：

(8)

式中：zi—各連桿質心坐標的Z軸值；mi—各連桿的質量。

建立拉格朗日方程可得：

(9)

式中：L=E-V，FI—慣性力。

將式(7，8)代入上式，化簡可得：

(10)

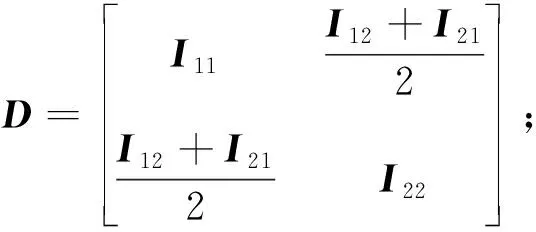
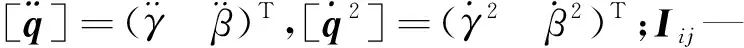
2.2 外力分析

設作用在動平臺上的外力為F，均可簡化為過旋轉中心O點的力矩Ms：

Ms=F×r

(11)

式中：r—外力F作用點到旋轉中心O點的矢量。

2.3 動力學模型建立

綜合式(10，11)，根據虛功原理，將慣性力FI和外力Ms映射到相應關節上的驅動力矩：

(12)

式中：JT—力雅克比矩陣。

根據式(12)建立的動力學模型可知，肩關節機構驅動力與慣性力和外力兩者有關。其中，慣性力大小受速度、加速度和姿態影響，而外力僅與姿態有關。

2.4 動力學仿真驗證

給出肩關節機構的結構參數如表1所示。

表1 肩關節機構結構參數

外力F=[1 1]N·m，并給出一組動平臺的運動方程：

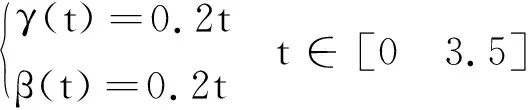
(13)

基于上述動力學模型，將肩關節機構的結構參數和運動方程代入式(12)中，并利用Matlab軟件計算得到肩關節機構的關節驅動力矩。

為了驗證動力學模型的正確性，本研究利用ADAMS動力學仿真軟件對肩關節機構進行動力學仿真，且添加各類約束條件和外力，使得仿真與理論計算的環境保持一致。筆者將仿真得到的驅動力矩與理論計算值進行比較，如圖3所示。

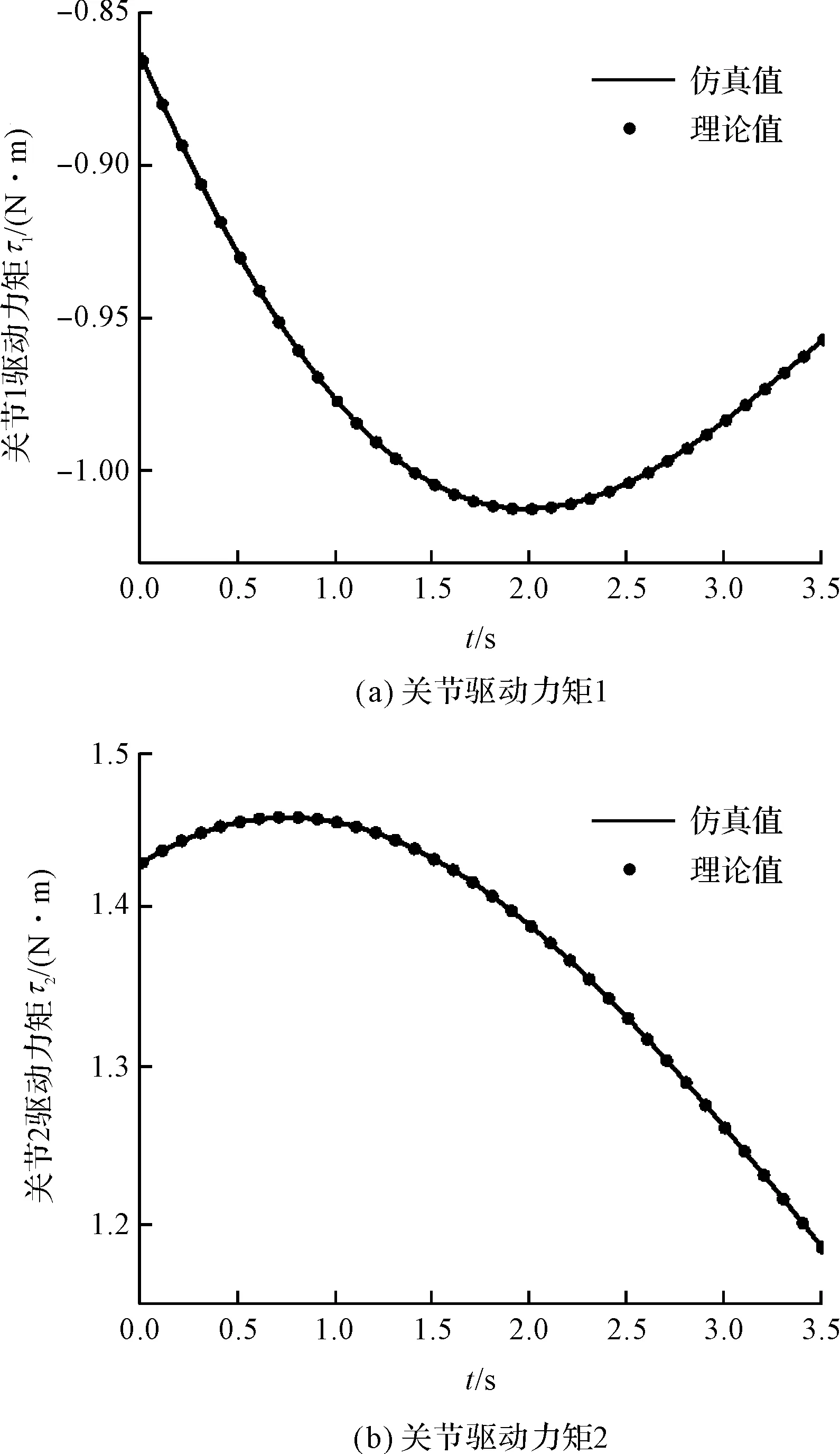
圖3 關節驅動力矩理論值與仿真值

通過對比可得：驅動力矩的理論值與仿真值兩者基本相等，故驗證了動力學模型的正確性。

3 肩關節機構的性能分析

3.1 動力學性能評價指標

肩關節機構不同的運動狀態會影響驅動力的大小，其中，速度、加速度會直接影響機構慣性力的大小。而肩關節機構一般作低速運動，速度較小，故忽略速度對慣性力的影響，只考慮加速度對慣性力的影響，因此式(10)可簡化為：

(14)

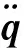
(15)

將式(15)求導，化簡可得：

(16)

式中：λ—矩陣DTD的特征值。

由式(16)可知：在工作空間W內，λ隨機構姿態變化而變化，且λ值越小表明由加速度引起的慣性力越小，因此將km作為動力學傳遞性能評價指標：

(17)

km數值越大，表示肩關節機構的動力學傳遞性能越好，則km在工作空間W的全域值為：

(18)

且肩關節機構存在多個輸入力矩，其差值越大則動力學傳遞性能越差，因此將kmc作為動力學傳遞均衡性能評價指標：

(19)

kmc數值越接近于1，表示肩關節機構的輸入力矩偏差越小，其動力學傳遞均衡性能越好，則kmc在工作空間W的全域值為：

(20)

3.2 力映射性能評價指標

由動力學模型可知，慣性力和外力通過虛功原理，將其映射為關節的驅動力矩。其中，力雅克比矩陣JT代表該映射關系，其值受機構姿態影響，即：

τ=JTτF

(21)

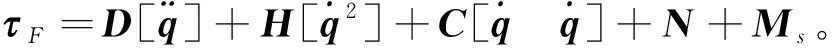
由于在工作空間W內，rank(J)=2，力雅克比矩陣JT可以奇異值分解，存在正交陣U∈R2×2和V∈R2×2，使：

JT=UΛV

(22)

設歐拉坐標系上的廣義力τF為單位向量可得：

τTU(ΛΛT)-1UTτ=1

(23)

當廣義力τF為單位矩陣時，關節驅動力矩分布在橢圓上；σi值越大，表明廣義力轉換到關節驅動力矩的效率越高，因此將kJ作為力傳遞性能評價指標[17-20]：

kJ=σ2

(24)

kJ數值越大，表示肩關節機構的力傳遞性能越好。則kJ在工作空間W的全域值為：

(25)

當σ1=σ2時，關節驅動力矩分布在圓上，關節驅動力矩之間的差值最小，因此將kJc作為力傳遞均衡性能評價指標：

(26)

kJc數值越接近于1，表示肩關節機構的力傳遞均衡性能越好，關節驅動力矩之間的偏差越小。則kJc在工作空間W的全域值為：

(27)

4 肩關節機構的動載協調分配優化

在穩定外載荷作用下，要求肩關節機構從起點運動到終點，但由于其運動軌跡和運動狀況的不確定性，存在多組運動方式。本文先依據性能指標得到性能最優的軌跡，再通過遺傳算法優化求解最優廣義時間，使得肩關節機構在能耗最低、時間最快、性能最好的情況下完成運動。

4.1 性能最優路徑規劃

為綜合考慮動力學性能和力映射性能因素，筆者采用加權求和法，將上述多性能指標轉換成單性能指標。

通過式(18，20，25，27)，分別求解出各性能指標在全域范圍內最大值kimax和最小值kimin，則不同姿態下的各性能指標可表示為：

(28)

式中：Ki—性能指標在全域變換范圍內的比值，Ki值越大，機構性能越好。

綜合考慮上述4個性能指標的影響，構造綜合性能指標函數：

(29)

式中：δi—目標比重系數。

δi值越大表示該衡量指標越重要。本文δi均等于1，將各性能指標視為相同比重，且Kmin值越小，機構的綜合性能越好。

給定機構起點q0=[0 0]T，終點qt=[-1.5 1]T，在起點至終點區域，均勻采樣n個控制點(每個控制點代表一種運動姿態，即動平臺運動經過的點)，且每個控制點對應一個綜合性能指標值。從起點運動到終點，建立路徑規則。從起點出發，可以到達相鄰3個控制點(控制點1、控制點2和控制點4)；之后，再從某一個控制點出發，可以達到下一個相鄰的3個控制點；以此類推，最終達到終點。

路徑規則如圖4所示。

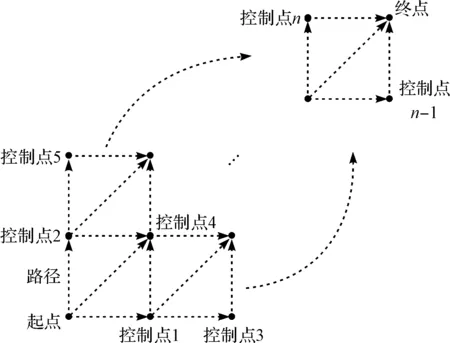
圖4 路徑規則

采用上述方式，可以得到數個由控制點組成的路徑。根據式(29)，筆者將一條路徑上所有控制點的綜合性能指標值求和，代表該條路徑的綜合性能。采用Dijkstra算法優化求解出從起點到終點的最優路徑，滿足路徑最短、綜合性能最好。

性能最優路徑如圖5所示。

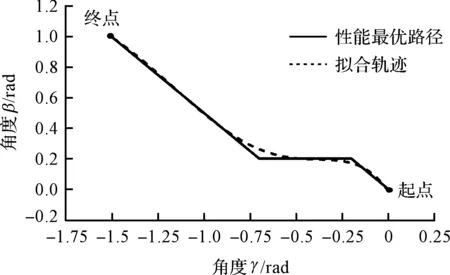
圖5 性能最優路徑

由于規劃出的路徑為折線，無法實現光滑軌跡運動，基于上述性能最優路徑的結果，本研究采用B樣條曲線擬合方法構造動平臺運動軌跡，并得到動平臺運動方程：

(30)

式中：u—路徑中第u個控制點，u∈[0，15]。

4.2 廣義時間優化

根據上述建立的性能最優軌跡可知，動平臺的運動軌跡與參數u有關。通過建立參數u與時間t的函數，可以進一步確定機構的速度特性。因此，建立參數u關于時間t的函數：

u(t)=a0+a1t+a2t2+a3t3+a4t4

(31)

式中：ai—時間函數的系數。

由于機構需要滿足起點和終點的位置約束條件，且在起點和終點處速度為零，故建立時間約束方程：

(32)

式中：u0=0，u1=15；T—機構完成運動的時間。

同時，考慮肩關節機構的關節驅動器輸出速度和力矩存在最大值，故建立關節輸出約束方程：

(33)

為實現肩關節機構在最短時間內完成運動，建立時間優化目標函數：

(34)

機構在運動過程中，可能存在時間很短而能耗很大或者關節力矩變化很大的情況，屬于不理想的工作狀況。因此，需要考慮能耗和關節力矩因素，故建立能耗優化目標和力矩波動優化目標：

(35)

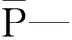
(36)

式中：Fτ—力矩波動優化目標，為機構關節運動的力矩變化率，衡量關節力矩的波動情況。

綜合考慮時間、能耗和力矩波動，建立廣義時間優化目標函數：

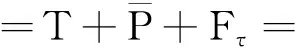
(37)

則優化過程如下：首先根據式(30，31)計算出動平臺的角度和角速度；其次通過式(1，2)得到關節驅動角度和角速度；然后根據式(13)動力學模型計算出關節驅動力矩；通過式(37)得到廣義時間優化目標函數；采用遺傳算法對時間函數式(31)進行優化求解，得到最優的廣義時間。設定種群個數為100，基因數為80，迭代代數為110，變異概率為0.1，交叉概率為0.5。

廣義時間優化結果如圖6所示。

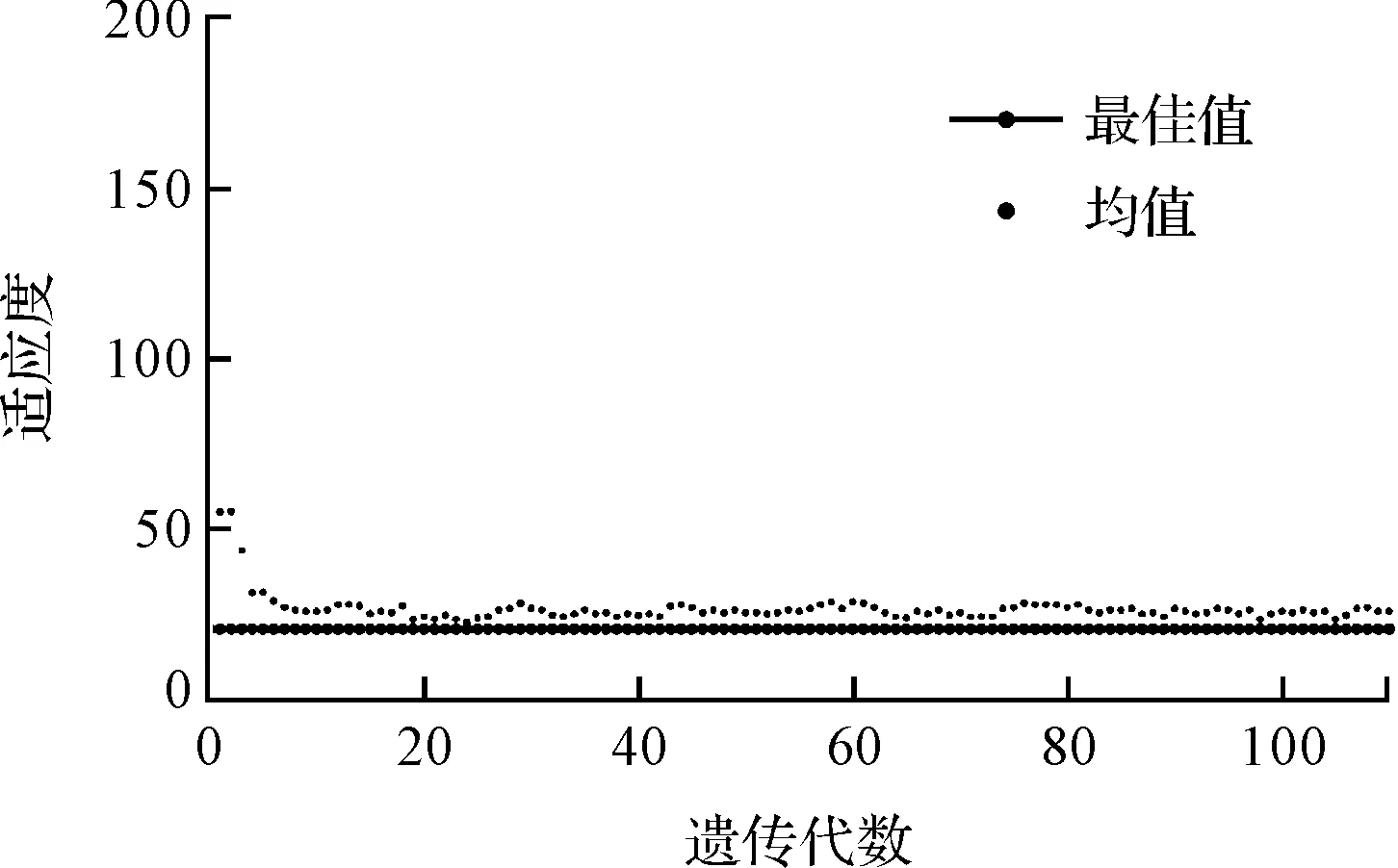
圖6 廣義時間優化結果

由圖6可知：經過數代運算后收斂，得到優化結果為：時間T=2.03 s；時間函數系數a0=0，a1=0，a2=8.85，a3=-1.58，a4=-0.48。將優化結果代入式(31)得到時間函數，并根據式(1，2，12，30)，通過Matlab軟件計算，得到優化后關節驅動力矩、關節角速度。

關節驅動力矩如圖7所示。

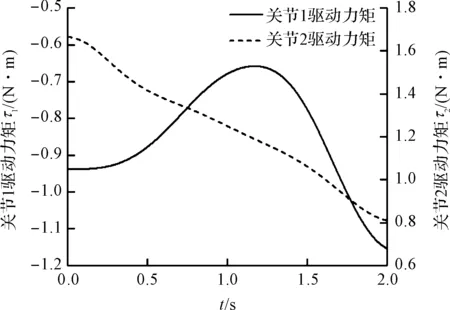
圖7 關節驅動力矩

關節角速度如圖8所示。

圖8 關節角速度

由圖7和圖8可知：關節驅動力矩和關節角速度均為光滑曲線，不存在突變現象，說明優化后，關節驅動器能夠實現平穩運行。在起點和終點時刻，關節輸出角速度均接近于零，符合實際運動狀況。兩個關節的驅動力矩和角速度值均處于同一數量級，數值大小接近，說明該優化方法能夠把機構慣性力和外力合理地分配到兩個關節上，說明采用上述動載協調分配優化方法，肩關節機構能夠在時間最短、能耗最低、性能最好的條件下完成運動。

5 結束語

本研究結合拉格朗日方程和虛功原理，建立了肩關節機構的動力學模型，并用動力學仿真軟件驗證了上述動力學模型的正確性；然后基于動力學模型，構建了動力學性能指標和力映射性能指標，采用加權求和法將各性能指標轉換為綜合性能指標，并利用Dijkstra算法求解得到綜合性能最優的軌跡；最后基于性能最優軌跡，考慮時間、能耗和力矩波動3個因素，建立廣義時間優化目標函數，采用遺傳算法優化時間函數，得到最優的廣義時間。

通過上述動載協調分配優化，使得肩關節機構能夠在時間最短、能耗最小、性能最好的條件下完成運動。