基于動態PSO優化HSMM的轉轍機PHM模型研究

戴乾軍,陳永剛,陶榮杰

(蘭州交通大學自動化與電氣工程學院,蘭州 730070)

轉轍機是鐵路信號系統中實現道岔操縱的重要設備，對保證行車安全、提高運營效率至關重要[1-2]。轉轍機結構復雜、數量多，故障發生帶有明顯隨機性和不確定性。目前鐵路電務部門沿用傳統的“故障修”和“計劃修”已很難適應軌道交通的快速發展。

文獻[3]結合D-S證據理論信息融合算法對轉轍機進行診斷研究。文獻[4]運用快速貝葉斯網絡實現S700K轉轍機的故障診斷研究。文獻[5]采用灰色神經網絡實現S700K轉轍機的故障診斷研究。文獻[6]結合小波分析對電動轉轍機動作電流實現分析研究。文獻分析說明:(1)目前對轉轍機故障的研究主要集中在電氣方面，然而實際故障絕大部分為機械故障[7]；(2)各種智能的故障診斷方法得到行業專家的肯定；(3)轉轍機的研究主要局限在故障診斷方面，缺乏設備全生命周期的機械狀態實時監控與故障預測。

隨著設備“計劃修”向“狀態修”的轉變，引入PHM理念評判轉轍機當前健康狀態并建立故障退化模型，預測轉轍機從當前狀態到故障發生的時間，對于鐵路部門提高維修效率、增大設備的安全可靠性以及及時給出維修決策具有極其重要的意義[8-10]。

近年來，設備PHM中建立隱半馬爾科夫(HSMM)的退化狀態模型受到廣泛的關注[11-13]，能有效而準確地描述設備退化過程的狀態轉移和故障規律的演化。動態粒子群(PSO)算法具有收斂性好、魯棒性強、能克服復雜系統預測模型易陷入局部最優的缺陷且能提高分類精度等優點。為提高模型的預測分類精度，引入動態PSO算法優化HSMM模型實現，轉轍機PHM技術研究。

1 轉轍機故障退化劃分

通過分析轉轍機的設備構造、故障機理，再結合故障數據、專家意見并分析故障演化規律、劃分退化模式。將轉轍機全生命周期的退化狀態劃分為4個狀態:正常狀態0、退化狀態1、退化狀態2和退化狀態3，見表1。

表1 轉轍機退化過程狀態劃分

2 HSMM基本理論

HSMM是在隱馬爾科夫(HMM)的基礎上引入狀態駐留時間的擴展模型。HSMM的一個狀態對應若干觀測值，模型的一個狀態代表宏觀狀態，多個微觀狀態組成一個宏觀狀態，HSMM結構圖如表2所示[16-17]。

表2 HSMM節描述

結合文獻[16]對HSMM模型的介紹，分析故障退化數目N，退化狀態觀測值M，狀態轉移矩陣A，觀測值概率矩陣B，狀態持續時間d和初始概率矩陣π，進而建立HSMM一般退化狀態模型λ=(π，A，B，Pi(d))，求得觀測值O=(o1，o2，…，ot)的概率P(O/λ)。

3 PSO算法的改進

PSO是一種智能優化算法，按一定的規則逐次迭代搜尋粒子群的全局最優值gbest和粒子個體最優值pbest。每個粒子在搜索空間內的飛行速度由粒子群和粒子個體的飛行經驗動態調整[18]。設粒子搜索空間D維，總粒子數Q，向量Xi=(xi1，xi2，xi3，…，xid，…，xiD)為粒子當前位置，向量Vi=(vi1，vi2，vi3，…，vid，…viD)為粒子當前速度。在每次迭代過程中，每個粒子根據式(1)分別朝著gbest和pbest更新飛行速度和位置。

(1)

其中，1≤i≤Q，1≤d≤D；w為慣性系數；c1、c2為加速因子，為保證粒子具有較強的自我更新和全局尋優學習能力，一般取c1=c2=2；r1、r2是[0，1]上的偽隨機數。

通常為實現粒子群的最大搜索能力，在迭代過程中粒子群個體尋優能力逐漸降低，全局尋優能力逐漸變強。故此結合式(1)對參數w、c1和c2進行改進。

3.1 改進慣性系數

采取常用的線性方式優化慣性系數，?w∈[wmin，wmax]滿足

(2)

式中，r、rmax分別為當前迭代次數與最大迭代次數；w′為第r次迭代后改進的慣性系數；wmax、wmin分別為迭代過程中慣性系數的最大、最小值。

3.2 改進加速因子

通常加速因子有同步時變和異步時變兩種優化方式。同步時變按線性關系對兩個加速因子進行同步變換，異步時變隨時間對兩個加速因子進行獨自改進。采取異步時變算法在迭代過程中逐漸減小c1、逐漸增大c2，公式如下

(3)

最后改進的動態PSO算法的數學模型為式(4)

(4)

其中，1≤i≤Q，1≤d≤D。

故此可實現動態PSO算法對HSMM模型進行參數優化。

4 改進模型的參數估計

HSMM主要解決模型的評估、解碼和學習問題，通過觀測序列來預測模型的狀態。本文采用“前向-后向”算法訓練已知模型的數據，并獲得模型各個狀態駐留時間的均值和方差。由觀測序列O和給定模型λ=(π，A，B，Pi(d))計算觀測序列的概率P(O/λ)，實現系統狀態評估[16]。

4.1 前向變量的模型參數估計

前向變量為t-d時刻由不同狀態在t時刻轉移到狀態j的概率。通過遞歸前向變量αt(i)，得到其遞推過程如下。

(1)前向變量

αt(j)=P(O1，O2，O3，…，OT，qt=j|qt+1≠j，λ) (5)

其中，1≤t≤T。

(2)t=0時刻

α0(i)=πj，1≤i≤N(6)

(3)從t-d時刻到t時刻前向變量遞歸公式

(7)

其中，1≤t≤T-1，1≤j≤N。

(4)計算概率

(8)

4.2 后向變量的模型參數估計

后向變量為t時刻由不同狀態在t+d時刻轉移到狀態j的概率。通過遞歸后向變量βt(i)，得到其遞推過程如下。

(1)后向變量

βt(j)=P(Ot+1，Ot+2，Ot+3，…，qt=i|qt+1≠i，λ) (9)

其中，1≤t≤T-1，βT(j)=1，1≤j≤N。

(2)從t時刻到t+d時刻后向變量遞歸公式

(10)

其中，t=T-1，T-2，…1，1≤j≤N。

(3)計算概率

(11)

4.3 模型參數估計的優化設計

結合給定的前向-后向變量算法與給定的觀測序列O確定模型λ，得到P(O/λ)重估計。

(13)

(2)狀態轉移矩陣A，aij為狀態i到狀態j的轉移次數的期望與從狀態i開始發生轉移總次數的比值。若定義t時刻給定模型和觀測序列在狀態i停留時間d，在t+d時刻轉移到j的概率εt，t′(i，j)存在

(14)

推導可得

(15)

(3)觀測值概率矩陣B={bj(k)}N×M，重估計bj(k)=P(ot=vk|qt=Sj)，其中bj(ok)為狀態j時刻觀測矢量值k的概率。由于HSMM模型一個狀態對應一節的觀測值，則狀態j持續d個時間單元后特定觀測值概率滿足

bj(k)=bj，d(ot+1;t+d)=P[O[t+1;t+d]|S[t+1;t=d]=j] (16)

(17)

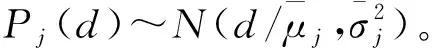
5 模型退化狀態識別及故障預測

5.1 改進模型的故障預測框架

改進的算法應用到故障狀態識別及剩余壽命預測，算法流程如圖1所示。

圖1 故障預測基本算法流程

5.2 改進模型的故障預測

根據全生命周期數據建立HSMM模型，計算各狀態駐留時間的概率密度函數pj(d)的均值μ(hi)和方差σ2(hi)，可將各狀態持續時間表示為

T(hi)=μ(hi)+ρσ2(hi) (20)

故而可通過以下遞歸算法預測狀態j的剩余使用壽命(RUL)，RULj表示狀態j時的剩余使用壽命。

(1)狀態為j-1

RULj-1=aj-1，j-1[T(hj-1)+T(hj)]+aj-1，j[T(hj)]

(2)狀態為j-2

RULj-2=aj-2，j-2[T(hj-2)+T(hj-1)]+aj-2，j-1RULj-1

(3)狀態為j

RULj=aj，j[T(hj)+T(hj+1)]+aj，j+1RULj+1

5.3 實例分析

以某鐵路局電務段S700K轉轍機為例，實驗中分別采集50組單個轉轍機的運行數據，前20組用于模型訓練，后30組用于模型測試。狀態數目設置為4，訓練算法最大迭代步數100，算法收斂誤差0.000 001。圖2為優化模型的訓練曲線，橫縱坐標分別為訓練步數與不同狀態下的似然概率估計值。測試模型的狀態轉移概率、健康狀態駐留時間的均值和方差分別見表3、表4和表5。該方法在4個模型中迭代曲線訓練步數不超過50的情況下達到訓練設定的誤差。可以看出模型具有較強的數據處理能力。

圖2 動態優化模型的訓練曲線

表3 狀態轉移概率

表4 退化狀態駐留時間均值和方差

表5 各狀態駐留時間

5.4 健康狀態評估

通過前文對轉轍機退化狀態的分析和劃分，建立與各狀態相對應的健康狀態評估分類器。對5.3節中的30組測試數據進行去噪，歸一化處理形成觀測序列O。通過訓練模型，得到其健康狀態轉移概率矩陣如表6所示。

表6 健康狀態轉移概率

表7和表8通過將轉轍機模型改進前后的健康狀態識別率作比較，結果表明基于動態PSO算法優化的HSMM模型健康狀態識別率明顯高于傳統HSMM模型。

表7 傳統HSMM模式識別結果

表8 改進算法優化的HSMM模型識別結果

5.5 剩余壽命估計

模型剩余壽命(RUL)估計中首先評估采樣點退化狀態，再按照數據選取標準并避開訓練樣本采集數據區域，轉轍機每個退化狀態選2個樣本測試數據。結果表明8個測試數據中只有在正常狀態0和退化狀態2分別出現一次錯誤預測，其余均正確。預測結果準確率較高，實驗結果如表9所示。

表9 剩余壽命預測結果

6 結論

(1)首先通過分析轉轍機退化狀態機理，將轉轍機全生命周期的健康狀態化為4個狀態。

(2)建立轉轍機的一般退化狀態的HSMM預測模型，再引入動態PSO算法對HSMM模型進行優化。

(3)然后采用前向-后向算法對改進的預測模型進行參數重估計。

(4)最后選取實驗數據對改進算法進行訓練，再結合現場數據驗證了該改進模型具有更好的故障預測性健康狀態識別能力。