有向相依網絡的可控性研究

陳世明，程運洪，鄧兵

（華東交通大學 電氣與自動化工程學院，江西 南昌 330013）

在過去幾十年中，復雜網絡研究吸引了許多來自不同科學領域學者的關注[1]。而以往的工作主要集中在對網絡拓撲結構復雜性及其與網絡動力學行為之間關系的研究，通過對復雜網絡拓撲性質、復雜網絡演化模型以及動力學行為的分析，揭示出隱藏在復雜系統中的一系列共同規律，對于把握復雜系統的宏觀特征及調節復雜系統上的動力學行為都將具有重要意義[2-3]。隨著對復雜網絡研究的進一步深入，復雜網絡可控性的研究得到了充分的關注與重視。Lin[4]給出了線性時不變控制系統“結構”和“結構可控性”的概念，并通過研究找到了結構可控性的充要條件；Liu等[5]基于線性時不變控制系統的結構可控性理論，對實際復雜系統進行了研究并建立了網絡結構可控性模型；Jia[6-7]發現了兩種不同的網絡控制模式：集中式控制和分布式控制；同時基于控制能力和隨機抽樣算法對有向復雜網絡的結構可控性做了進一步探索，隨后一些研究者通過改變連接邊的方向實現了網絡可控性的優化[8-10]。目前復雜網絡可控性研究已經取得了眾多的重要成果，但復雜網絡控制方面的研究仍然處于起步階段，還有很多未解決的理論問題，例如結構可控性理論無法適用于無向網絡、權重網絡和時變網絡的可控性等問題。針對結構可控性理論僅適用于有向網絡的局限性，Yuan[11]引入了嚴格可控性(exact controllability)的概念，證明完全控制復雜網絡所需的最少控制器數目由網絡矩陣特征值的最大重數決定，并提出了利用矩陣初等變換甄別網絡中需要被獨立控制的節點的方法，通過對大量真實網絡和模型網絡的計算結果表明了嚴格可控性理論的有效性和實用性；Li[12]針對實際網絡的分型特征，運用嚴格可控性理論對分型網絡的可控性進行了分析。基于單層有向網絡和無可控性進行的研究已取得了較大突破。但現實中的網絡通常是相互依存的，例如，公交–地鐵網絡、電力–通信網絡、電力–供水網絡等，且通過研究已經發現相依網絡的動態特性如級聯失效[13-17]、擴散現象[18]、演化博弈動力學[19]、同步性[20]等，均明顯區別于單層網絡。怎樣合理地控制相依網絡將是面臨的重要挑戰。Yuan[21]運用嚴格可控性理論對多重網絡的可控性進行了研究，發現在多關系網中存在主導關系網，其結構和連接權重對于整個網絡的嚴格可控性起主導作用；在多層網中，不同層間的連接方式以及疏密程度對整個網絡的嚴格可控能力都有重要的影響，并且發現在層間加入少量連接能夠大大提高整個網絡的可控能力。Nie[22]分析了多層網絡中層間連邊結構對網絡可控性能的影響，研究發現層間連邊比例較小時，網絡最少驅動節點的數目隨著連邊度相關性的增加而減小，層間連邊同配性強的網絡易于控制；當層間連邊比例較大時，則會出現相反的情況，層間連邊異配性強的網絡易于控制。然而以上研究僅分析了網絡層間的連接方式及網絡層間連接邊的度相關性對無向相依網絡可控性的影響，卻未考慮到實際網絡中存在有向網絡相互依存的情況，例如在交通網絡與供電網絡中，某一時間內列車的運行方向是定向的，同時供電系統按照列車運行的線路提供電力支持保證其正常運行。在供電網絡中某一處發生故障會通過網絡之間的相依關系，將其傳遞到交通網絡中從而導致經過這條線路的列車都無法運行，反之亦然。這樣在某個網絡中產生的故障會因為彼此間的相依關系，使得故障在兩個網絡之間相互蔓延，從而對網絡造成更大的破壞，由此表明有向相依網絡間的相依關系對整個有向相依網絡有重要影響。為了探究有向網絡間相依關系對網絡的影響，本文首先構建了基本的有向相依網絡模型，并結合嚴格可控性理論，給出了基于最少控制輸入的可控性評判指標；其次，針對相依方式對有向相依網絡可控性產生的影響，基于經典的有向隨機網絡(DER)和有向無標度網絡(DSF)，構建了DERDER、DER-DSF、DSF-DSF 3類有向相依網絡模型，并研究了隨機相依方式下3類網絡的可控性能；最后，基于隨機相依方式下對網絡可控性的分析，提出了3種有向網絡的相依方式：最高入度與最高出度節點相依(HI-HO)、最高入度與最低出度節點相依(HI-LO)、最低入度與最低出度節點相依(LI-LO)，且在既定的3種相依方式下對網絡的可控性進行了仿真分析。

1 有向相依網絡可控性

1.1 有向相依網絡

有向相依網絡由兩個有向子網絡(子網絡A和子網絡B)通過雙向連接線連接而成，表示子網絡A中的節點，節點數為；表示子網絡B中的節點，節點數為，子網絡之間的雙向連接線為網絡相依邊，其余單向連線為內部邊。F表示節點相依比例。F包括和，其中表示子網絡A的相依節點數占子網絡A總節點數的比例值，表示子網絡B的相依節點數占子網絡B總節點數的比例值，即

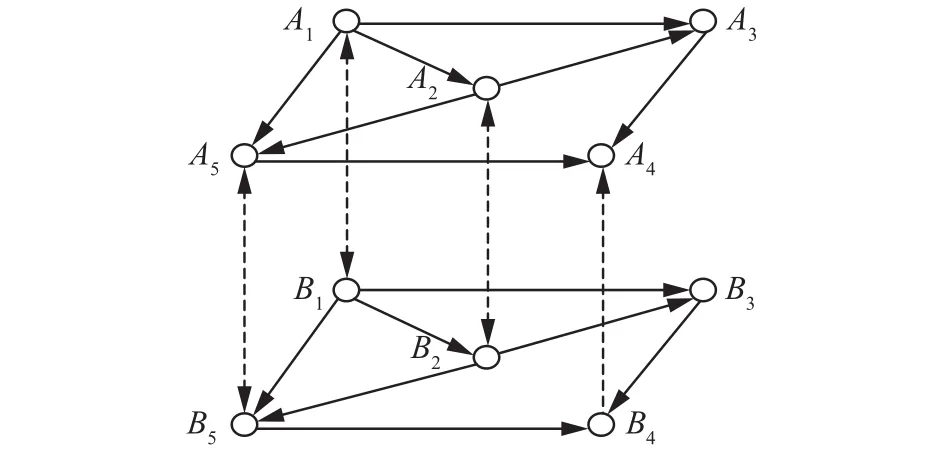
圖 1 有向相依網絡Fig. 1 The interdependent directed network

1.2 嚴格可控性

在現代控制理論中，如果通過一些控制變量的輸入能使一個系統從任意初始狀態達到理想狀態，我們稱這個系統是可控的。這里只考慮線性時不變系統并且假設系統內部未發生動態變化。有向相依網絡狀態方程為

定理1 對于一個可控系統來說，最少控制輸入個數是系統矩陣特征值中具有最大代數重數的特征值所對應的幾何重數。

1.3 理論分析

對于滿足狀態方程(2)的系統來說，其節點總數是不變的且為，若使得系統滿足其可控性，需通過外部控制輸入作用于系統節點。假設得到外部控制輸入作用的節點個數為，未作用的節點個數為，則

對于可控系統來說，必然存在一個得到外部控制輸入作用節點的最小個數，記為，使得系統達到可控要求，并且未作用的節點個數達到最大，記為，得

從而可得

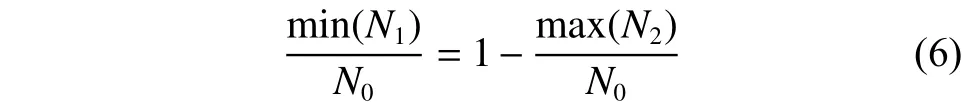
然而需要確定能夠達到控制效果所需的最少控制輸入個數。在這里將最小控制輸入個數定義為達到系統可控性要求時，輸入矩陣B秩的最小值，即

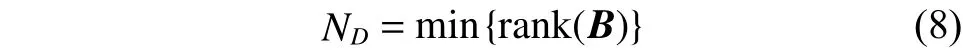
若滿足狀態方程(2)的系統是可控的，那么由PHB判定定理可知，對矩陣A的任意特征值，下式恒成立：

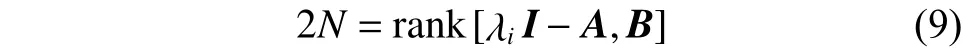
式中I為單位矩陣。

根據矩陣不等式關系得：

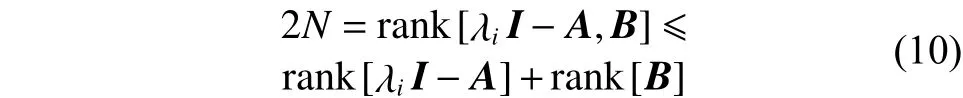
進一步得

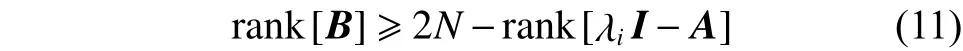
上式滿足恒成立關系，則：

進一步可得

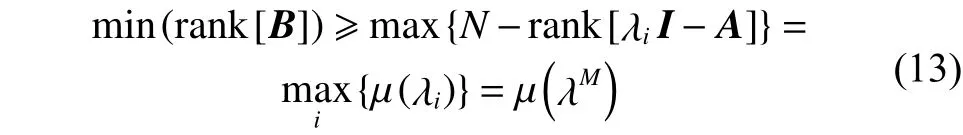
最后可得：

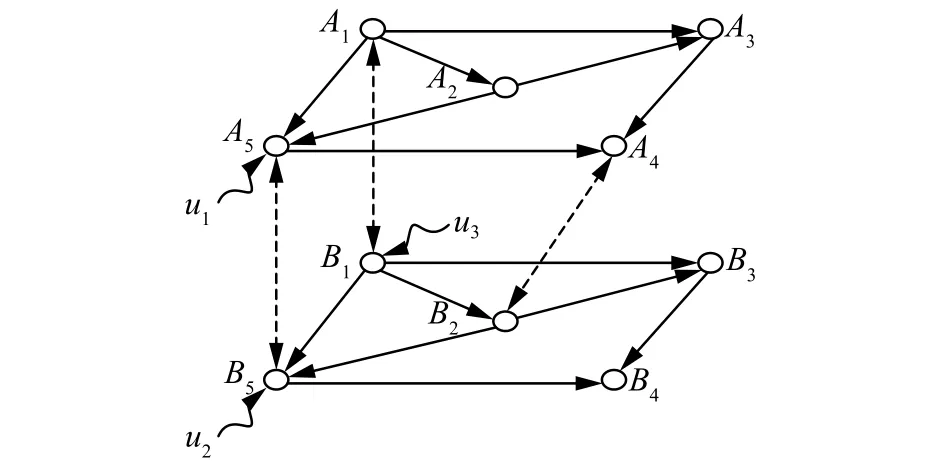
圖 2 有向相依網絡可控性Fig. 2 Controllability of the interdependent directed network

2 隨機相依方式下網絡可控性的仿真與分析

本文基于經典的有向隨機網絡(DER)和有向無標度網絡(DER)，構建了DER-DER、DER-DSF、DSF-DSF 3類有向相依網絡模型。同時在隨機相依方式下，對不同相依比例的DER-DER網絡可控性進行了獨立仿真實驗。

在隨機相依方式下，通過對4組不同相依比例的DER-DER網絡可控性進行多次仿真，其中網絡規模，T為實驗次數，；相依比例為。從圖3(a)中可以發現在相依比例時，在區間內出現明顯的波動，即網絡可控性在這一范圍內出現很大的隨機性；同時結合圖3(b)、3(c)、3(d)可知，在相依比例、0.4、0.8時，同樣在一定范圍內出現較大的波動。這表明，在同一相依比例下，隨機的相依方式使得網絡可控性表現出明顯的差異性，即有向網絡的相依方式直接影響著網絡的可控性。

通過對比以上4組不同相依比例下的網絡可控性發現，隨著相依比例F的逐漸增加，逐漸減小，即隨著相依比例的增加，網絡可控性逐漸增強。為了充分證明相依方式直接影響著有向相依網絡可控性，我們在隨機相依方式下對連續相依比例的3類有向相依網絡的可控性進行了仿真分析。

圖 3 單一相依比例下DER-DER網絡的可控性Fig. 3 Controllability of DER-DER network with a single dependency ratio

在隨機相依方式下，通過對連續相依比例的DER-DER、DER-DSF、DSF-DSF這3類有向相依網絡的可控性進行仿真，如圖4(a)所示，就DERDER有向相依網絡而言，隨著相依比例F的逐漸增加，總體呈現逐漸減小的趨勢，但由于相依方式的隨機性，DER-DER有向相依網絡中存在，的情況，同時在圖4(b)所示的DER-DSF有向相依網絡與圖4(c)所示的DSF-DSF有向相依網絡中均呈現與圖4(a)相同的變化規律，即網絡可控性在隨著相依比例增加而增強的過程中會出現一定程度的波動，從而表明有向相依網絡的可控性不僅與相依比例有著緊密相關，更與有向網絡的相依方式有著密不可分的關系，上述分析為有向相依網絡可控性的研究提供了充分條件。

圖 4 連續相依比例下網絡的可控性Fig. 4 Controllability of the network under continuous dependency ratio

3 有向相依網絡的相依方式及其可控性對比分析

基于隨機相依方式下對有向相依網絡可控性的分析，本文提出了有向網絡之間的3種相依方式：最高入度與最高出度節點相依(HI-HO)、最高入度與最低出度節點相依(HI-LO)、最低入度與最低出度節點相依(LI-LO)，同時針對3種相依方式構建了如圖5所示的簡單有向相依網絡模型并分析了其可控性。

圖 5 有向相依網絡的相依方式Fig. 5 Dependent way of the interdependent directed network

針對提出的3種有向網絡相依方式，在DERDER、DER-DSF、DSF-DSF 3類有向相依網絡中對網絡可控性進行了仿真對比。如圖6(a)所示，在DER-DER有向相依網絡中對3種既定相依方式而言，均呈現隨著相依比例F增大而減小的趨勢，同時在圖6(b)所示的DER-DSF有向相依網絡與圖6(c)所示的DSF-DSF有向相依網絡中，的變化趨勢與圖6(a)相同，即在同一有向相依網絡中對任一既定相依方式來說，網絡可控性會隨著相依比例的增加而逐漸增強。在圖6(a)所示的DER-DER有向相依網絡中，針對相同相依比例，對3種既定相依方式下的網絡可控性進行對比發現(LI-LO)＜(HI-LO)＜(HI-HO)，同時在圖6(b)所示的DER-DSF有向相依網絡與圖6(c)所示的DSF-DSF有向相依網絡中，在同等相依比例下有(LI-LO)＜(HI-LO)＜(HI-HO)，即在同一網絡中相同相依比例下，基于最小入度與最小出度節點相依的有向相依網絡可控性最強，而基于最大入度與最大出度節點相依的有向相依網絡可控性最弱。

圖 6 不同相依方式下有向相依網絡可控性Fig. 6 Controllability of the interdependent directed network under different dependent way

4 結束語

相互依存的復雜網絡廣泛存在于實際復雜系統中，且往往存在有向網絡之間的相依，本文首先構建了基本的有向相依網絡模型，并結合嚴格可控性理論，給出了基于最少控制輸入的可控性評判指標；考慮相依方式對有向相依網絡可控性產生的影響，本文基于經典的有向隨機網絡(DER)和有向無標度網絡(DSF)，構建了DER-DER、DER-DSF、DSF-DSF 三類有向相依網絡模型，并在4組不同相依比例下，研究了隨機相依方式下的DER-DER網絡的可控性能，研究發現，隨著相依比例的增加，網絡可控性逐漸增強。但每組相依比例下的網絡可控性均會在一定范圍內出現大幅的波動。為了進一步證實相依方式影響著網絡的可控性，通過在隨機相依方式下對連續相依比例下的3類有向相依網絡可控性進行了仿真，我們發現隨著相依比例的逐漸增加，網絡可控性總體均呈現逐漸增強的趨勢，但由于相依方式的隨機性，網絡可控性在增強過程中會出現明顯的波動情況，即有向網絡的相依方式對網絡可控性產生著重要影響。

基于分析本文提出了3種有向網絡的相依方式：最高入度與最高出度節點相依(HI-HO)、最高入度與最低出度節點相依(HI-LO)、最低入度與最低出度節點相依(LI-LO)，同時就提出的3種相依方式在3類有向相依網絡中對網絡可控性進行了仿真對比，且通過對比發現，在同一網絡中同等相依比例下，基于最低入度與最低出度節點相依的有向相依網絡可控性最強，而基于最高入度與最高出度節點相依的有向相依網絡可控性最弱。研究證實了有向網絡相依方式密切影響著網絡的可控性，且得到3種相依方式下有向相依網絡可控性的強弱關系，這為構建強可控性能的實際有向相依網絡提供了參考依據。