快速雙非凸回歸算法及其電力數據預測應用

王鋒華，成敬周，文凡

（1. 國網浙江省電力公司，浙江 杭州 310000; 2. 國網浙江省電力公司 經濟技術研究院，浙江 杭州 310000）

電網是加快工業進步、提高居民生活質量、保持社會穩定健康發展的基礎。因此，電網的發展具有重要的意義。電網企業的責任是確保安全、經濟、清潔和可持續的能源供應，從而為社會、經濟的健康發展，人民生活水平的逐步提高保駕護航。其中，產能輸出和運營指標管理作為電網企業經營活動的中樞，是企業發展的重中之重，能對企業整體運營狀況、管控經營、監控戰略產生實效。此外，通過挖掘數據資產的潛在價值，不僅能提升企業各部門的專業管理能力，而且還能促進企業安全、有序、健康、高效地運營，對決策制定發揮重要的輔助作用。然而，確定和下達經營決策的合理性取決于預測這些指標未來變化情況的準確性，由于預測電網企業運行運營指標是面向未來的，且影響指標變化的因素較多，因此預測過程具有很大的隨機性和不確定性。結合電網企業的實際情況設計合適的預測方法，將直接關系到預測實施的精度。

目前，常用的傳統預測方法有指數平滑法(exponential smoothing，ES)[1]、線性回歸分析法(linear regression analysis，LRA)[2]、時間序列法(time series method，TS)[3]等，ES 認為時間序列的態勢具有穩定性或規則性，所以時間序列可被合理地順勢推延，且它認為最近的過去態勢，在某種程度上會持續到未來，所以將較大的權數放在最近的資料上。LRA利用稱為線性回歸方程的最小平方函數對一個或多個自變量和因變量之間的關系進行建模的一種回歸分析。TS則通過編制和分析時間序列，根據時間序列所反映出來的發展過程、方向和趨勢，進行類推或延伸，借以預測下一段時間或以后若干年內可能達到的水平。雖然這些傳統方法在預測應用中略有成效，但是它們預測對象單一、過度依賴歷史數據，且無法考慮到未來預測過程中存在的不確定性因素。

因此，針對以上問題，一些學者嘗試將神經網絡應用到預測中去，使得預測系統具有一定的智能信息處理能力，取得了不錯的預測效果。但是，由于神經網絡采用的是經驗風險最小化原則，容易陷入局部極小點且收斂速度慢，這極大地限制了該方法在實際過程中的應用。基于支持向量機的預測模型[4]很好地克服了神經網絡的這一缺點，SVM采用結構風險最小化原則，整個求解過程轉化為凸二次規劃問題，能得到全局最優解。但是，由于SVM是借助二次規劃來求解支持向量，而求解二次規劃將涉及m階矩陣的計算(m為樣本的個數)，當m數目很大時該矩陣的存儲和計算將耗費大量的機器內存和運算時間。因此，其不適用于大規模訓練樣本。

為此，本文提出一種雙非凸回歸(double nonconvex regression，DNR)算法用于標量電力數據預測。該方法首先將稀疏編碼技術[5]轉化為回歸預測應用，再采用lp范數替換原始的重構誤差l2范數以及表示系數l1范數等約束，以獲得更為靈活的模型目標泛函形式。最后，利用交替方向乘子法(alternating direction method of multipliers，ADMM)[6]優化求解目標函數；其中，為獲得快速的子問題優化效果，提出一種改進的迭代閾值方法用于求解lp約束子問題，保證全局最優解并可實現并行實施方案。在電網企業運行運營指標真實數據上的實驗結果表明該方法切實可行，且具有很高的預測精度。

1 雙非凸回歸算法

稀疏編碼技術[5]已在模式識別領域得到廣泛的應用，其通過誤差平方最小化和稀疏性范數約束搜尋目標量的最佳逼近系數。原始的稀疏回歸模型可以描述為

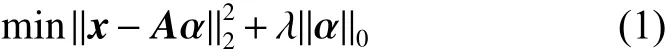
遺憾的是，受l0偽范數約束影響，最小化式(1)是一個NP難問題，僅能在有限樣本集中運行實施[7]。一般將之調整為Lasso問題，即通過l1范數替換l0范數

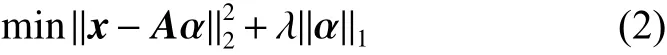
已有理論表明，在一定的不連貫條件下[7]，l1最小化問題很大概率等價于l0最小化問題。而且，l1范數是最逼近于l0范數的凸約束形式，有利于模型的優化求解。

此外，式(1)和式(2)中所采用的l2范數最小化重構誤差僅適合于高斯分布噪聲環境[8-9]。為適應特定的樣本或特征干擾，常采用等價于拉普拉斯分布的l1范數約束進行誤差最小化[5]，即

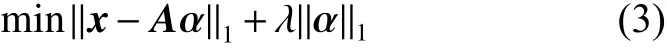
然而，當矩陣A的不連貫條件無法滿足，或重構誤差并不適應于常規的高斯分布或拉普拉斯分布時，模型(3)的求解結果往往是次優的。針對此問題，本文采用lp范數(p∈(0, 1]))替換式(3)中的l1范數約束，即

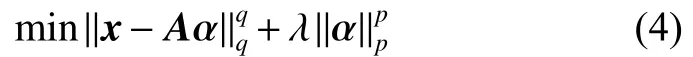
為便于區分，在重構誤差中以符號q表示lp范數約束。式(4)為本文所提回歸模型的目標函數，對誤差項和正則項都采用非凸函數約束，因此稱之為雙非凸回歸算法(double nonconvex regression, DNR)，其中對α約束lp范數較l1更接近于l0，使得重構系數α具有更強的稀疏性；對誤差約束lp范數使之更貼近于橢圓分布[10]，具有較高斯分布和拉普拉斯分布更為寬泛的適用范圍。

2 模型優化求解

針對常規的單lp約束稀疏回歸問題，迭代重加權最小二乘(IRLS)[11]、迭代重加權l1最小化(IRL1)[12]、交替方向乘子[6]以及迭代閾值收縮(IST)[13]等求解算法都得到了成功應用。然而，對于式(4)所示雙非凸約束模型，所述求解算法都無法直接應用。如果強行將迭代重加權型算法擴展為雙加權凸約束形式，所得解也非常容易陷入局部最優；ADMM算法能夠進行有效地多變量拆分，但是要求各子優化問題具有閉式解或快速求解策略；IST具有高效的收斂性能，但前提需將目標函數中的觀測矩陣A變換至正交形式。結合所述分析，本節采用ADMM算法和IST算法融合策略進行目標函數式(4)的求解優化。首先，通過ADMM變量拆分，獲得部分子問題的閉式解；其次，提出改進的迭代閾值算法進行非凸子問題優化；最后，給出完整的模型求解算法并分析其運算復雜度。

2.1 ADMM變量拆分

考慮到DNR模型包含兩個非凸lp范數約束，需要引入兩個輔助變量用于問題簡化，將式(4)轉化為等價約束優化式

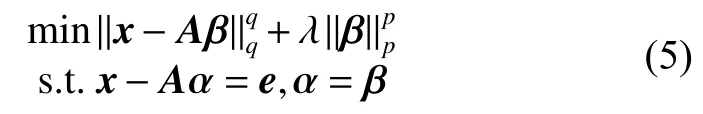
并得到其增廣拉格朗日形式

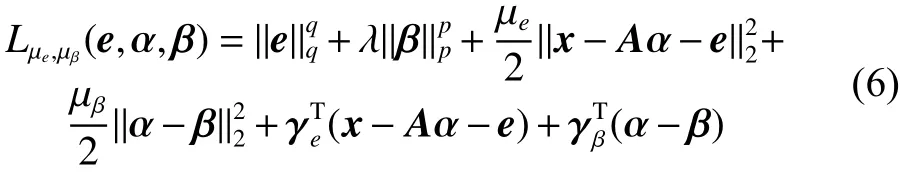
式中：μe、μβ＞0 為懲罰參數，γe和 γβ為拉格朗日乘子系數。根據ADMM變量分離規則，式(6)包含以下迭代步驟：

1) 固定 α 和 γβ，βk+1的更新子問題為

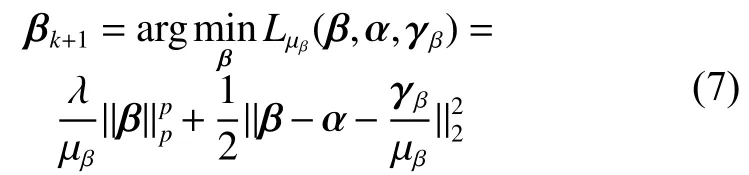
2) 固定 α 和 γe，ek+1的更新子問題為

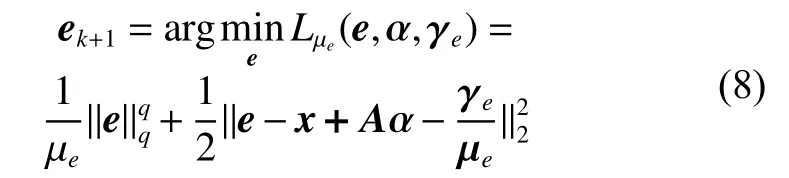
3) 固定 e、β、γe和 γβ，αk+1的更新子問題為

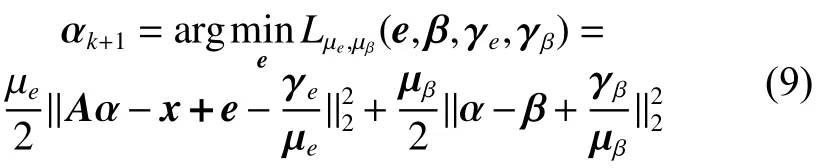
4) 根據計算所得的 β、e 和 α1，更新 γe和 γβ

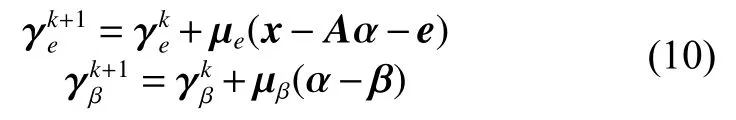
上述迭代步驟中，式(10)是ADMM固有的乘子升級規則。式(9)通過微分后可得αk+1的解析解：

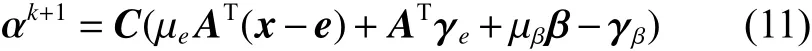
式中：在給定μe和μβ的前提下，逆算子C=(μeATA+μβI)-1是常量，可提前計算并緩存，加速算法的求解效率。因此，非凸子問題(7)和(8)是求解式(6)的關鍵步驟。考慮到p次lp范數約束的可疊加性，式(7)和式(8)得以分解成獨立且并行可解的標量子問題：

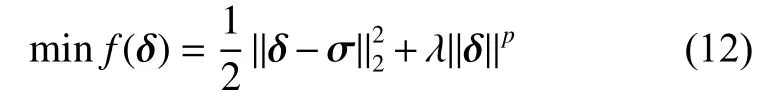
當p=1時，可由經典的軟閾值算法[14]進行有效求解。針對本文的非凸情況 (0＜p＜1)，IRLS、IRL1、IST等求解算法都存在局部次優解的缺陷。如圖 1所示，當 σ=0.9，p=0.2且 λ=1時，IRLS、IRL1和IST都陷入了局部最小值。為解決該問題，本文提出一種改進的閾值迭代方法，在保證高效求解的同時能夠獲得全局最優值。

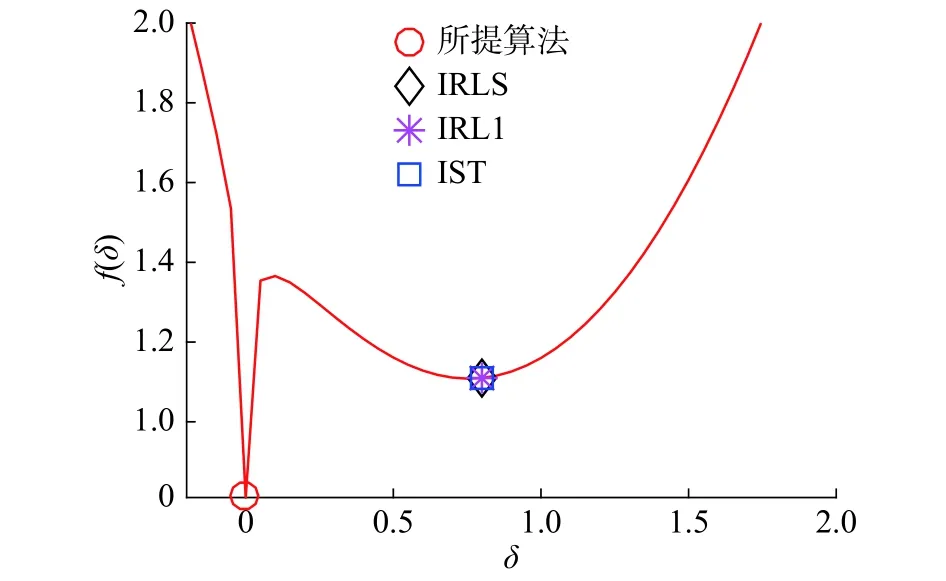
圖 1 幾種算法對典型非凸問題式(12)的最優解Fig. 1 Several algorithms for the optimal solution to the typical nonconvex problem in formula (12)

2.2 改進的迭代閾值優化算法

根據式(12)的對稱性以及閾值收縮規則[13]，當 σ＞0 時，最優解范圍為[0, σ]；當 σ＜0 時，最優解范圍為[σ, 0]。不失一般性，本節僅考慮σ＞0的情形。設p=0.6，λ=2.5，圖2給出了不同σ值下的f(δ)最優解情況。由圖2中可見，f (δ)的最小值取決于某臨界 σ 值 τσ，當 σ＜τσ時，minf (δ)位于 δ=0；當 σ≥τσ時，minf (δ)位于 δ＞0 的某個點。因此，求解式(12)的核心由τσ和δ兩個關鍵值確定。

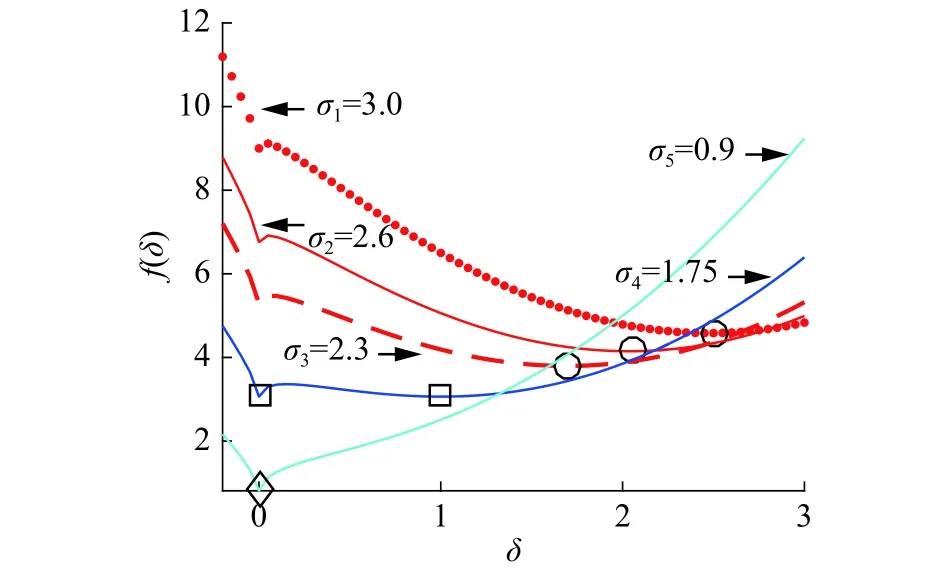
圖 2 不同σ值下非凸問題f (δ)的最優解Fig. 2 The optimal solution of non-convex problem f (δ)under different σ values

式(12)的一階和二階微分別為

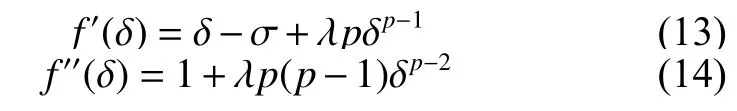
設 f"(δ(λ,p))=0，可得 δ(λ,p)=(λp(1-p))1/(2-p)。結合圖2 可知，當 δ∈(0, δ(λ,p))時，f(δ)是凹函數；當 δ∈(δ(λ,p), +∞)時，則 f(δ)是凸函數。進一步，為保證f(δ)在 (δ(λ,p), +∞)具有最小值，需滿足 f'(δ(λ,p))≤0，文獻[13]令 f'(δ(λ,p))=0 并計算出 τσIST用于迭代閾值求解。然而，該閾值設法存在問題，如圖1所示，IST計算所得的解滿足上述所有規則，且時保證

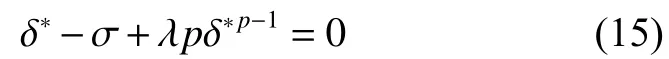
在 (δ(λ,p), +∞)中具有唯一的最小值。然而，f(δ*)具體取值依然高于 f(0)。

從圖 2 可見，存在特定的 τσ使得 f(δ*)=f(0)，當σ＜τσ時，δ=0 為 f(δ)的最小值；當 σ≥τσ時，f(δ)最小值在δ＞0的某個位置。因此，正確的閾值τσ和δ*計算公式應該為

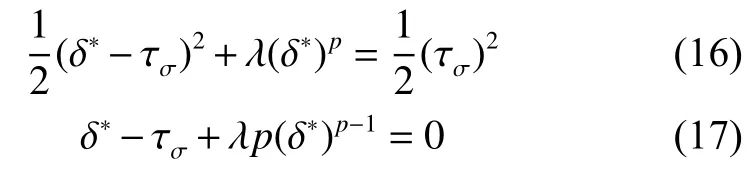
將式(17)中的τσ值代入式(16)可得

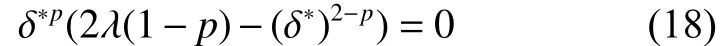
其最優解 δ*∈(δ(λ,p), +∞)為 δ*=(2λp(1-p))1/(2-p)，并可進一步計算出τσ為

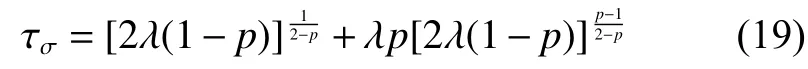
根據式(15)和式(19)，所提的迭代閾值規則如算法1描述。算法1主要更改了閾值計算策略，基本步驟與文獻[13]類似，當J=2時能夠獲得令人滿意的收斂結果。

結合算法1與ADMM優化框架，完整的DNR優化步驟按式(7)～(10)循環進行，具體的收斂條件按文獻[6]設定。值得注意的是，式(7)與式(8)由算法1并行計算實施，其計算復雜度僅為O(n)，而式(9)的計算復雜度在逆算子緩存的前提下為O(max(n2, nm))。假設ADMM迭代次數為t，則完整的算法復雜度為O(tnmax(n, m))，遠遠優于IRLS、IRL1等算法的O(n3)。

算法1 改進的迭代閾值規則

輸入 參數 σ，λ ，p，J；

輸出 δ*。

1) 按式 (19)計算 τσ值；

2) 如|σ|＜τσ；則令 δ*=0；

3) f反之，令 k=0，δk=σ；

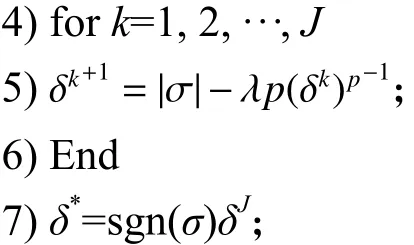
3 實驗分析

分別對電力企業運行中的全負荷電能輸出(兆瓦時)以及運營指標中的月利潤總額進行預測。首先對電力企業的產能輸出和運營數據進行實證分析，然后將所提算法與經典的SVM[15]、BP神經網絡[16]和非凸非光滑約束NNR方法[7]進行精度對比。

3.1 電能輸出預測

通過某電力企業復循環動力裝置(包括兩個燃氣渦輪，一個汽輪機以及兩個熱回收系統)6年運行數據作為預測樣本，共含該企業全負荷運行674天所產生的9 568個采樣點，樣本特征包括環境溫度(AT)、大氣壓力(AP)、相對濕度(RH)、排汽壓力(V) 4個維度。隨機選擇{10%, 20%, 30%,40%, 50%}個采集數據作為訓練樣本，其余作為測試數據。實驗精度由絕對誤差均值(MAE)和均方誤差(RMSE)兩者表示，其計算式分別為

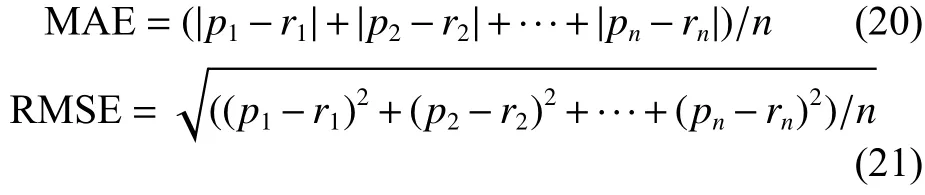
式中：p和r分別為預測值和真實值，n為測試樣本總量。

表1給出了SVM、BP神經網絡、NNR以及DNR三種對比算法在不同訓練樣本量下的預測精度對比，其中DNR的參數值p=q=1。從表1可見，DNR算法在不同的訓練數下都具有最低的誤差均值和均方誤差值，展示了更為優秀的預測精度。而且，DNR算法在30%～50%訓練樣本量下的精度非常接近，MAE基本穩定在4.95左右，而BP神經網絡、SVM和NNR在不同樣本量下的預測值跨度相對較大，說明DNR具有更高的算法穩定性，對輸入訓練樣本量要求更小。同時，DNR計算所得的AT、AP、RH、V這4個特征表示系數絕對值分別為 0.767、0.085、0.102、0.426，即 4個特征的預測貢獻度依次為AT＞V＞RH≈AP，與文獻[17]的理論分析結果吻合。此外，SVM、BP、NNR、DNR 3種算法在50%訓練量下的完整預測時間分別為 2.91 s、0.48 s、0.32 s和 0.06 s，可見 DNR 具有明顯更高的運行效率。最后，表2和表3分別給出了DNR算法在不同p、q值下的預測精度。從中可見，隨著p、q值的優選變化，DNR的預測精度得以進一步提升，驗證了非凸約束的優越性，且最優值處于 p、q∈[0.5, 0.8]，與文獻[18]的理論結論吻合。

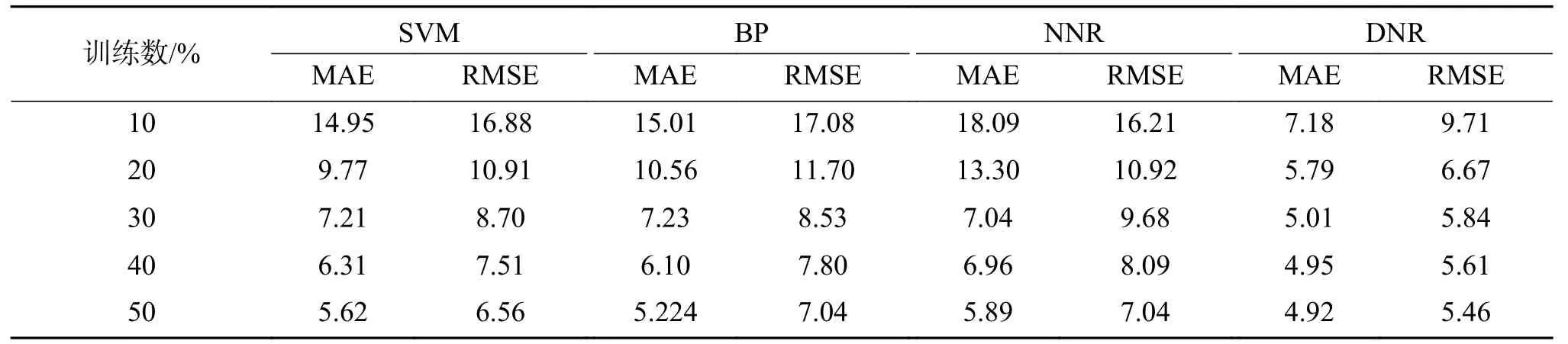
表 1 電能輸出預測精度對比Table 1 Comparison of prediction accuracy of energy output

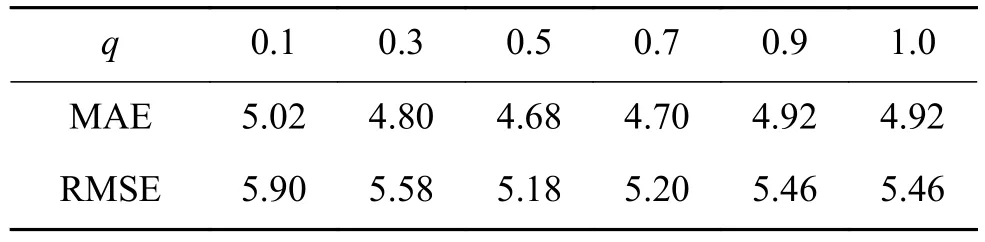
表 2 DNR算法不同q值下的電能輸出預測精度Table 2 Predicting accuracy of energy output in different q of DNR algorithm

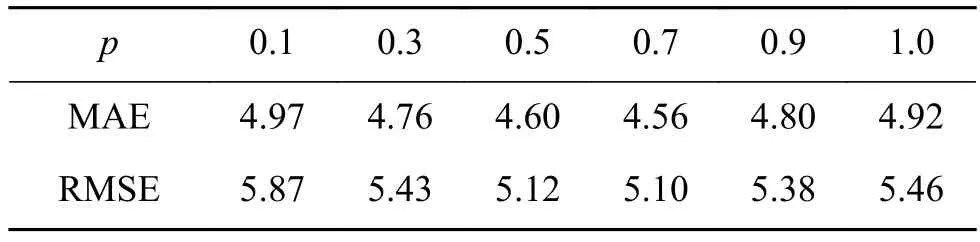
表 3 DNR算法不同p值下的電能輸出預測精度Table 3 DNR algorithm power output prediction accuracy in different p

3.2 運營數據預測

選取某電網企業自2013年1月—2014年12月期間的流動資產周轉率(次)，購電成本(萬元)，可控費用(萬元)，貨幣資金，主營業務利潤率，單位資產售電量，每萬元電網資產運行維護成本等真實數據作為訓練樣本集，2015年1月—2015年12月期間的運營指標數據作為測試樣本集。表4為部分訓練樣本集數據。

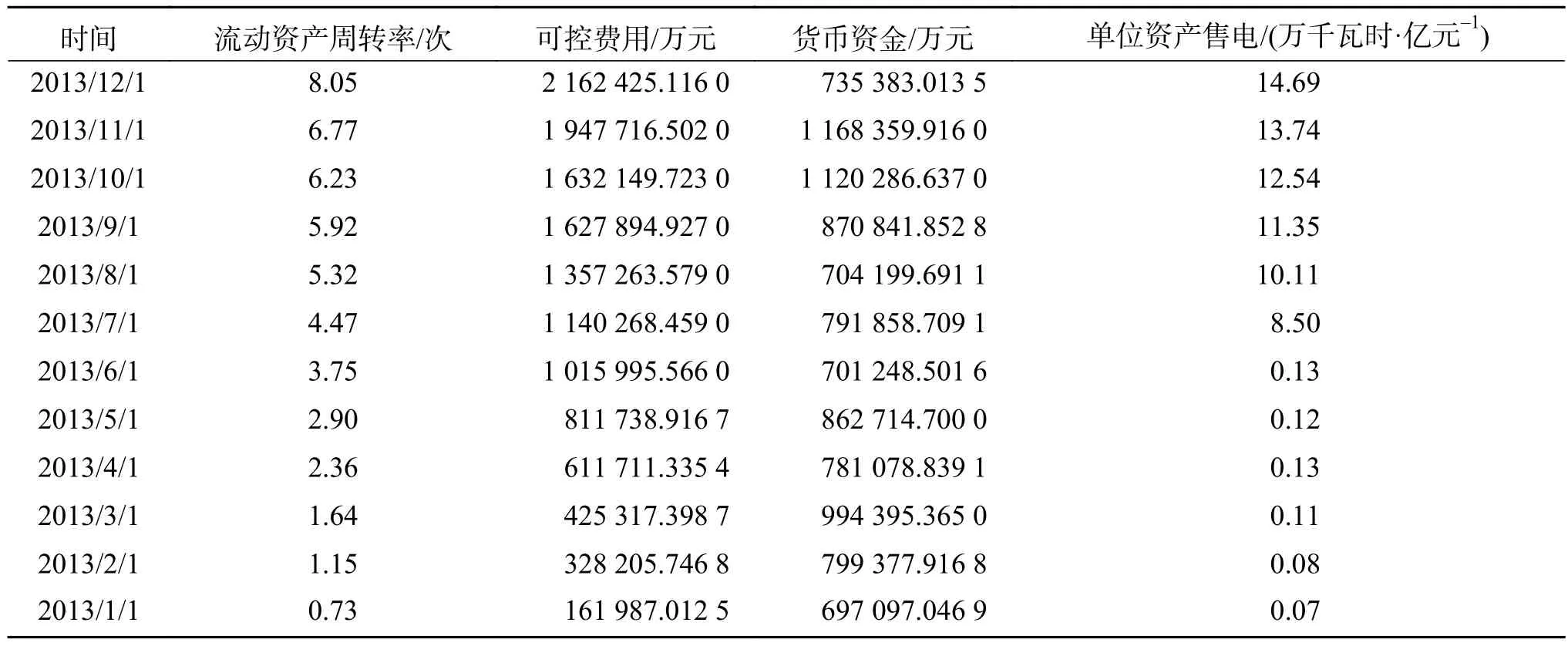
表 4 部分訓練樣本集數據Table 4 Partial training sample data set

實驗中通過DNR、SVM、BP神經網絡和NNR這3種預測方法對2013年1月—2014年12月連續2年的月利潤總額進行擬合，對2015年1月—2015年12月1年的月利潤總額進行預測，并比較三者的預測精度，其結果如圖3～6以及表5所示。

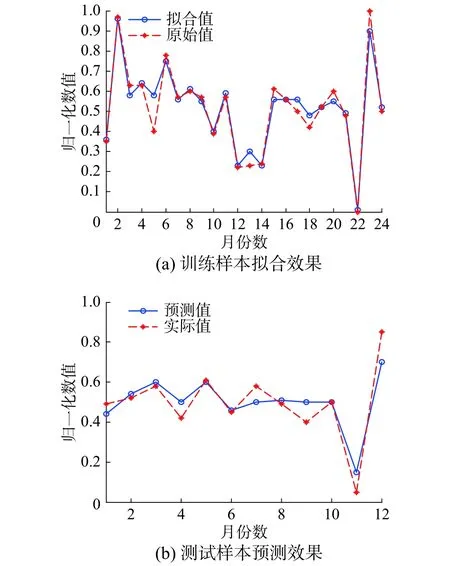
圖 3 DNR對訓練樣本的擬合效果及對測試樣本的預測效果對比Fig. 3 Comparison of the fitting effect of DNR on training samples and the prediction effect of test samples

由圖3可知，DNR對24個月數據的擬合值基本貼合原始值的走勢，表現出優秀的擬合能力。圖4中SVM的擬合能力一般，特別是第1個月～第11個月的擬合值與原始值相差較大。圖5中BP神經網絡對數據的擬合值符合原始值的一般走向，只是在數值上存在一定程度上的等比例縮小。由圖6可以看出NNR的擬合和預測誤差較大。而對于DNR、SVM和BP神經網絡的預測效果，通過圖3～6的預測對比可知DNR更為接近地預測出了2015年1月—2015年10月的月利潤總額。雖然其對11月～12月這兩個月的數據預測不甚理想，但整體利潤趨勢與實際值吻合。相較而言，BP神經網絡對這兩個月的數據預測較精準，但1月～4月的預測值卻與實際值相差甚遠。SVM的預測值與實際值雖大致在同一數值層上，但整體預測值離精確點相去較遠。此外，NNR雖與實際值走勢相似，但存在多個嚴重偏離真實值的預測值。

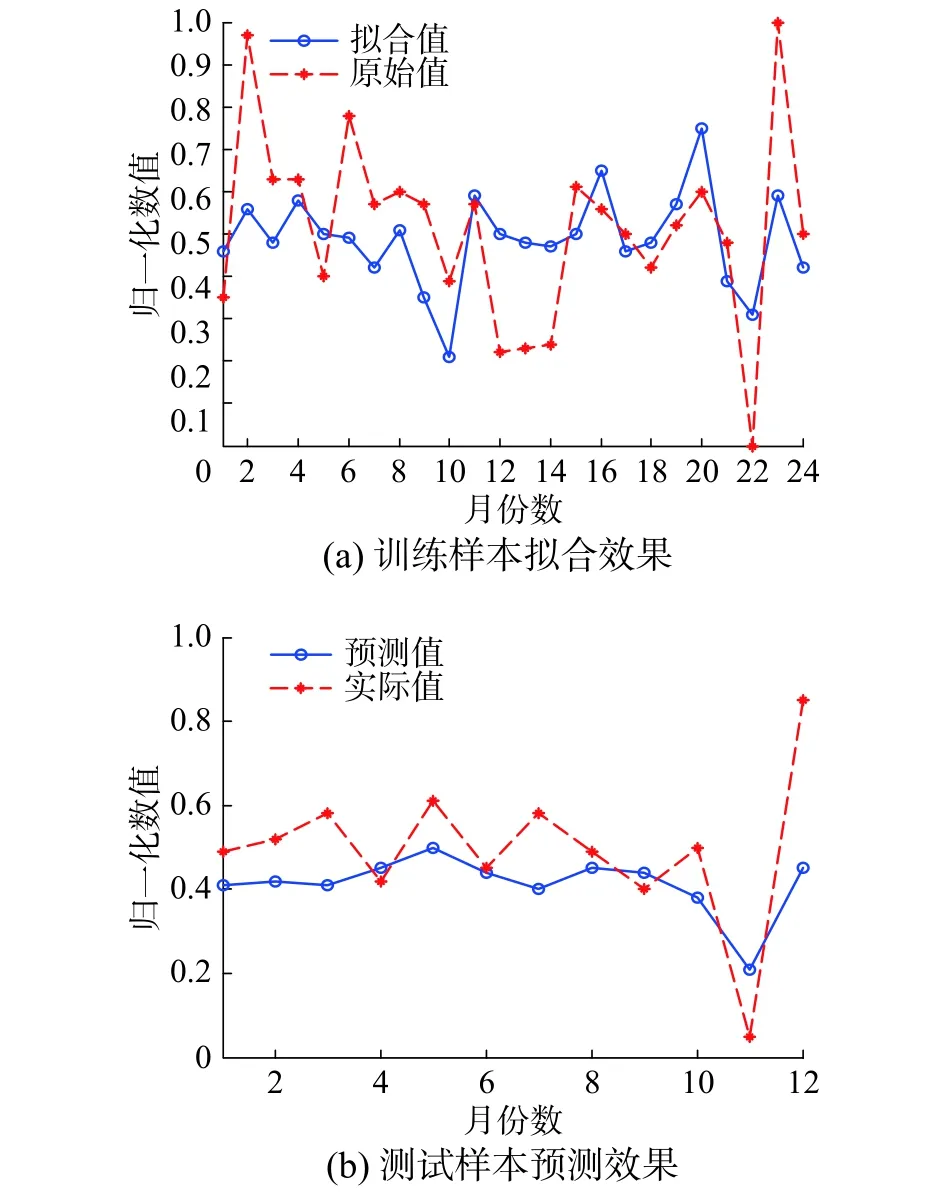
圖 4 SVM對訓練樣本的擬合效果及對測試樣本的預測效果對比Fig. 4 Comparison of test samples and training samples’s fitting effect by SVM

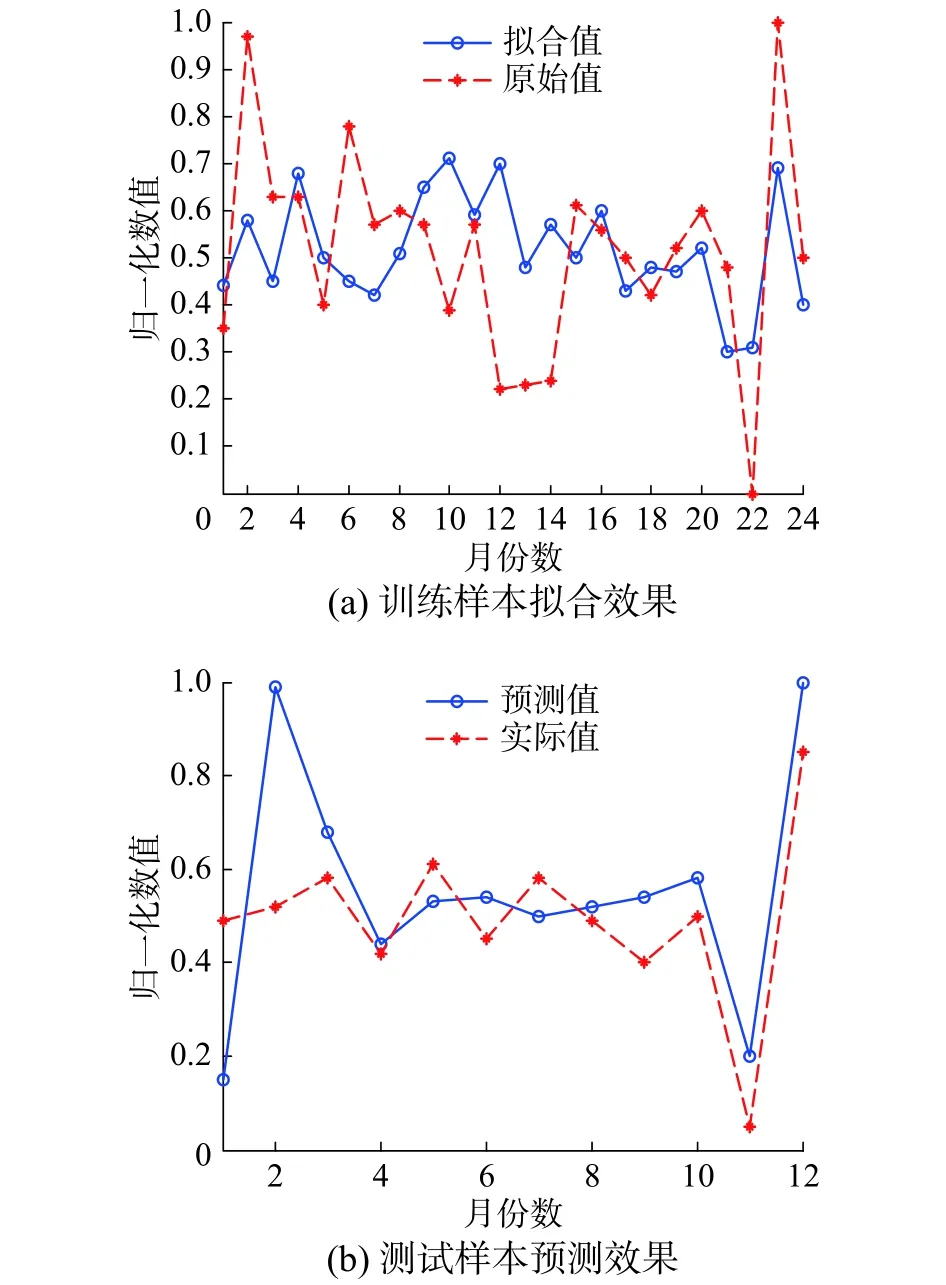
圖 5 BP神經網絡對訓練樣本的擬合效果及對測試樣本的預測效果對比Fig. 5 Comparison of test samples and training samples’s fitting effect by BP neural network

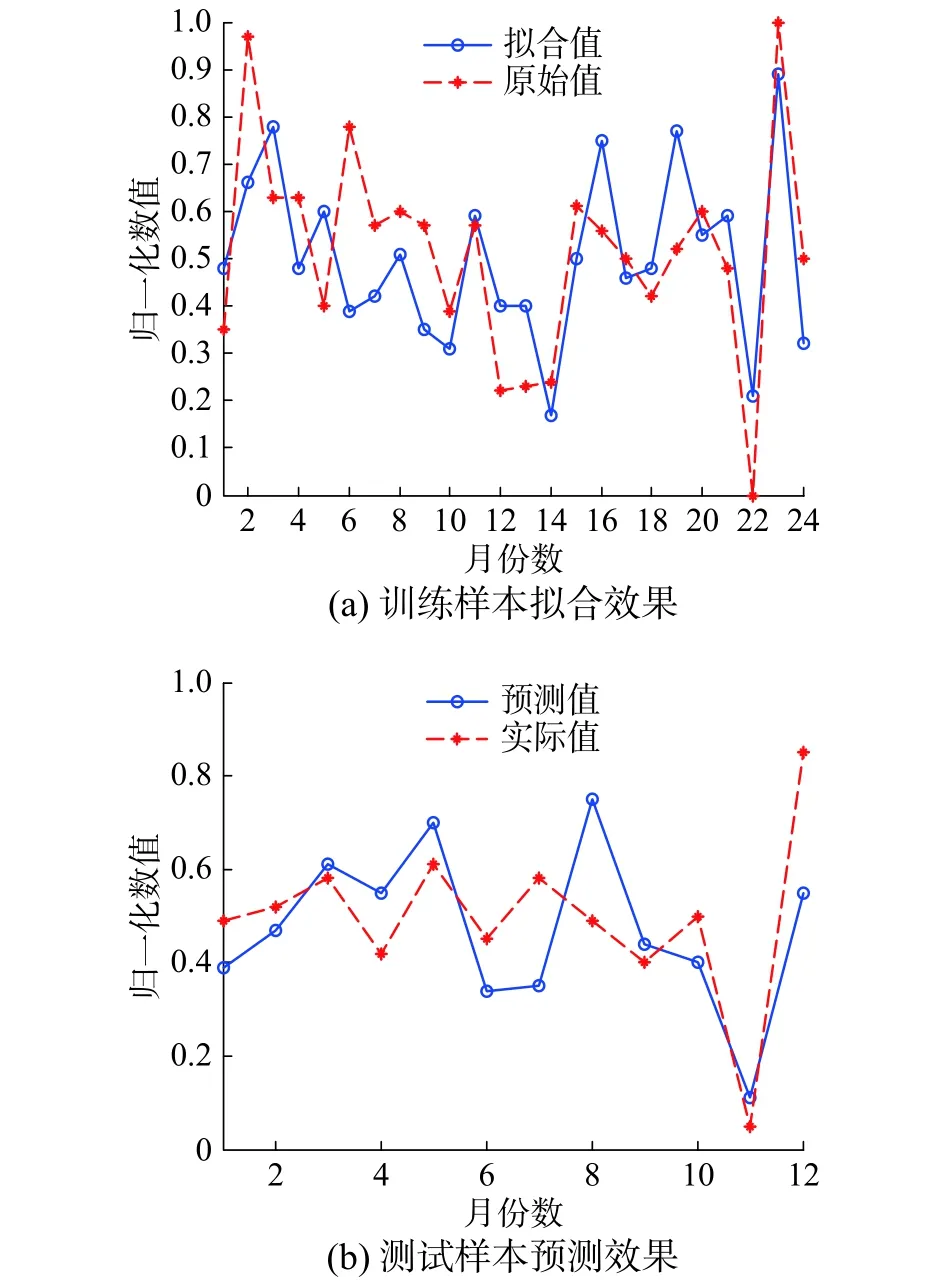
圖 6 NNR對訓練樣本的擬合效果及對測試樣本的預測效果對比Fig. 6 Comparison of test samples and training samples’s fitting effect by NNR

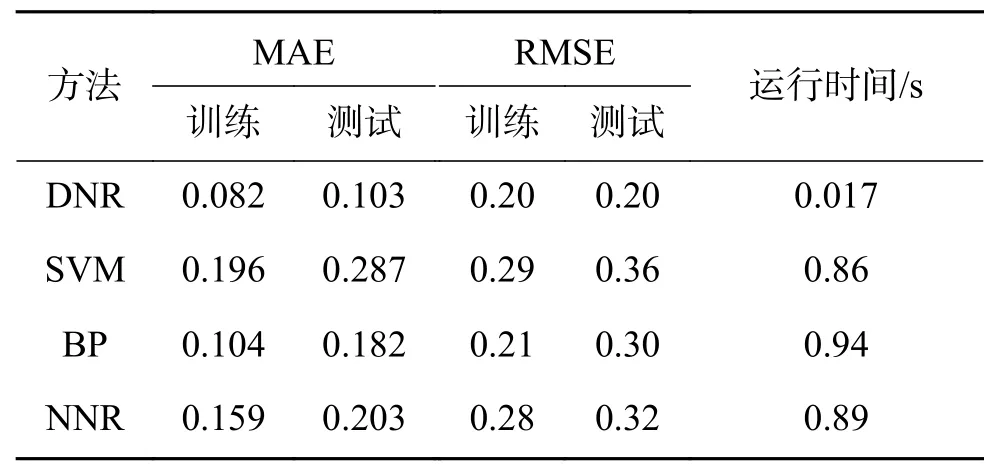
表 5 DNR、SVM、BP和NNR在運營數據中的預測對比Table 5 Predictive comparison of DNR, SVM, BP and NNR in operational data

綜上所述，DNR和BP神經網絡在運營數據中對訓練樣本的擬合效果優于SVM。雖然DNR和BP神經網絡的擬合效果接近，但對于測試樣本的預測結果對比圖中明顯可以看出，DNR的預測結果最佳。NNR因為存在多個高偏離度的預測點而次于SVM。BP神經網絡的預測效果最差。

此外，由表5可知，不論訓練樣本還是測試樣本，DNR的MEA和RMSE值均小于SVM BP神經網絡和NNR的誤差均值和均方差，再次驗證了圖3～6的擬合效果和預測效果，并且DNR的運行時間(單位：s)也遠遠少于SVM、BP神經網絡和NNR。

4 結束語

電網企業運行和運營數據預測是一個極為復雜的課題，數據采集過程中儀器老化產生的測量誤差、人工疏忽導致的漏檢誤標等因素使得預測過程具有很大的隨機性和不確定性。本文提出一種稱為非凸回歸的預測算法，改進了經典稀疏回歸法中的模型約束形式，對重構誤差和稀疏系數引入lp(0＜p≤1)正則化項約束，使之包含更為稀疏的目標項并具有更為靈活的擴展應用能力。通過交替方向乘子法對該回歸模型進行求解，并對其中的子問題提出一種新的閾值優化規則，確保目標函數具有快速的非凸優化求解能力。實驗結果表明，與支持向量機BP神經網絡和非凸約束算法NNR相比，本文所提方法具有較高的預測精度和更好的預測效果，且運行效率高。