帶擾動的變頻正弦混沌神經網絡研究

胡志強，李文靜，喬俊飛

（1. 北京工業大學 信息學部，北京 100124; 2. 計算智能與智能系統北京市重點實驗室，北京 100124）

自從Hopfiled和Tank用提出的Hopfiled網絡(Hopfiled neural network, HNN)開創性成功解決旅行商(traveling salesman problem, TSP)問題以來，神經網絡在解決優化問題中開始得到廣泛關注和應用[1]。由于HNN的算法依然采用傳統的梯度下降算法，極易陷入局部極小點，導致無法找到最優解[2]。Chen等[3]在Hopfield網絡基礎上引入自反饋，并加入模擬退火(simulated annealing,SA)機制，提出暫態混沌神經網絡(transient chaot-ic neural network, TCNN)，通過混沌的遍歷性和偽隨機性克服了HNN局部極小問題。混沌神經網絡(chaotic neural network, CNN)被證明是解決優化問題的有效工具[3-7]。隨后，Zhang等[4]采用小波函數作為激勵函數，提出了WCNN模型，用來解決函數優化問題；Liu等[5]在混沌神經元模型中加入遲滯動力，提出了HCNN模型，并應用于TSP問題中；Zhao等[6]引入高斯自反饋項，提出了CNNW模型，成功應用于組合優化問題。以上學者提出的CNN模型，雖然都在一定程度上提高了全局尋優能力，但是大都缺乏一定的生物學機制，無法表征神經元激勵與響應的頻幅關系，不能充分體現出復雜多變腦部活動的非線性動力學特征和具有更加豐富的混沌全局搜索性能。因此，Hu等[7]基于腦電波的生物機制，將變頻正弦函數(frequency conversion sinusoidal, FCS)與Sigmoid函數加權和組成非單調激勵函數，提出了變頻正弦混沌神經網絡(frequency conversion sinusoidal chaotic neural network, FCSCNN) 模型，進一步提高了TCNN的混沌動力學特性和全局尋優性能，更準確地解決了函數優化及TSP問題，驗證了模型有效性和可行性。

而人們研究TCNN的優化計算方法，歸根結底是希望能夠看到其在硬件上的實現，進而觀察和研究混沌神經元的狀態和響應，最終制造出混沌計算機[8]。但是，由于電子元器件或電路的不穩定性，在一定情況下，不可避免地會出現不同程度的擾動，這會對FCSCNN性能產生影響，所以對該模型的抗擾動能力進行實驗、評估、比較是很有必要的。因此，本文針對FCSCNN模型，通過引入不同程度的周期和非周期擾動，將其應用到函數優化和組合優化問題上，分析其抗擾動能力，仿真實驗證明了FCSCNN具有較強的魯棒性和抗擾動能力。

1 帶擾動的變頻正弦混沌神經元模型

TCNN多采用Sigmoid函數作為激勵函數，而非單調激勵函數比單調(Sigmoid)激勵函數更容易產生混沌，在尋優過程中具有更好的全局搜索性能[9-10]。基于以上理論以及腦電波的生物機制，FCSCNN模型獲得了較好的優化效果[7,11]。由于來自外界的擾動有周期的和非周期的，因此本文分別用代表周期擾動的三角函數和非周期擾動的小波函數來進行研究，在FCS神經元模型的基礎上加入擾動項，來分析模型的抗擾動能力。建立如下帶擾動的FCS混沌神經元模型：

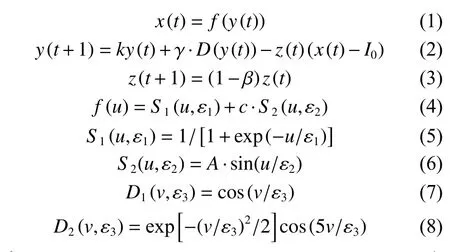
神經元的倒分岔圖和最大Lyapunov指數可以直觀體現出神經元的動力學特性。Lyapunov指數大于零(非正無窮)，證明模型具有混沌行為，并且值越大表明混沌程度越強[5]。Lyapunov指數定義為

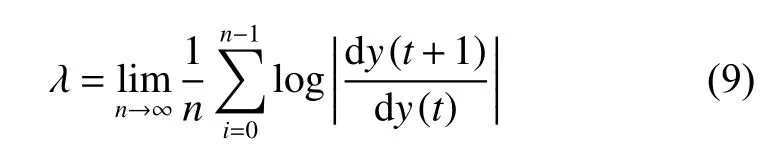
則對于帶擾動的FCS混沌神經元模型有

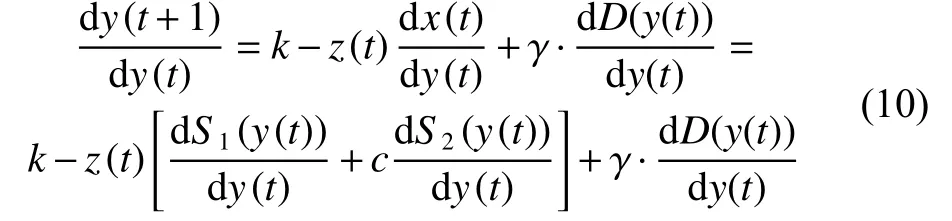
式(10)中第2項表達式同文獻[7]，第3項如下：

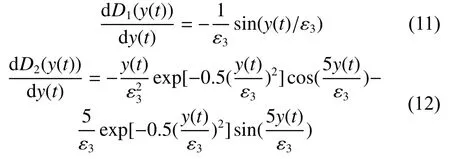
由文獻[7]可知，相同模型參數下，提出的FCS混沌神經元比標準的暫態混沌神經元具有更復雜和更豐富的混沌動力學行為，具有更多的正值Lyapunov指數，并且混沌搜索的時間更長，這都為混沌全局尋優提供了良好的動力學基礎。證實了提出的新的混沌神經元模型的有效性和可行性。

進而，為了驗證FCS混沌神經元模型的魯棒性和抗擾動能力，當設置擾動項為三角函數擾動時，當選取參數 k=1, β=0.004, ε1=0.02, I0=0.65,z(0)=0.9, A(0)= 0.6, ε2(0)=0.02, a=6, b=1, c=0.25,ε3=0.1固定不變時，分別取γ=0.002和γ=0.02時，FCS神經元的倒分岔圖和最大Lyapunov指數時間演化圖分別如圖1～2所示。

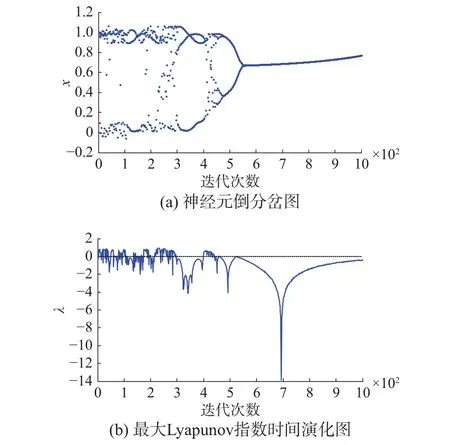
圖 1 帶三角函數擾動(γ=0.002)的FCS神經元倒分岔圖和最大Lyapunov指數圖Fig. 1 The reversed bifurcation and the time evolution of the maximal Lyapunov exponent of the FCS neuron within trigonometric function disturbance(γ=0.002)

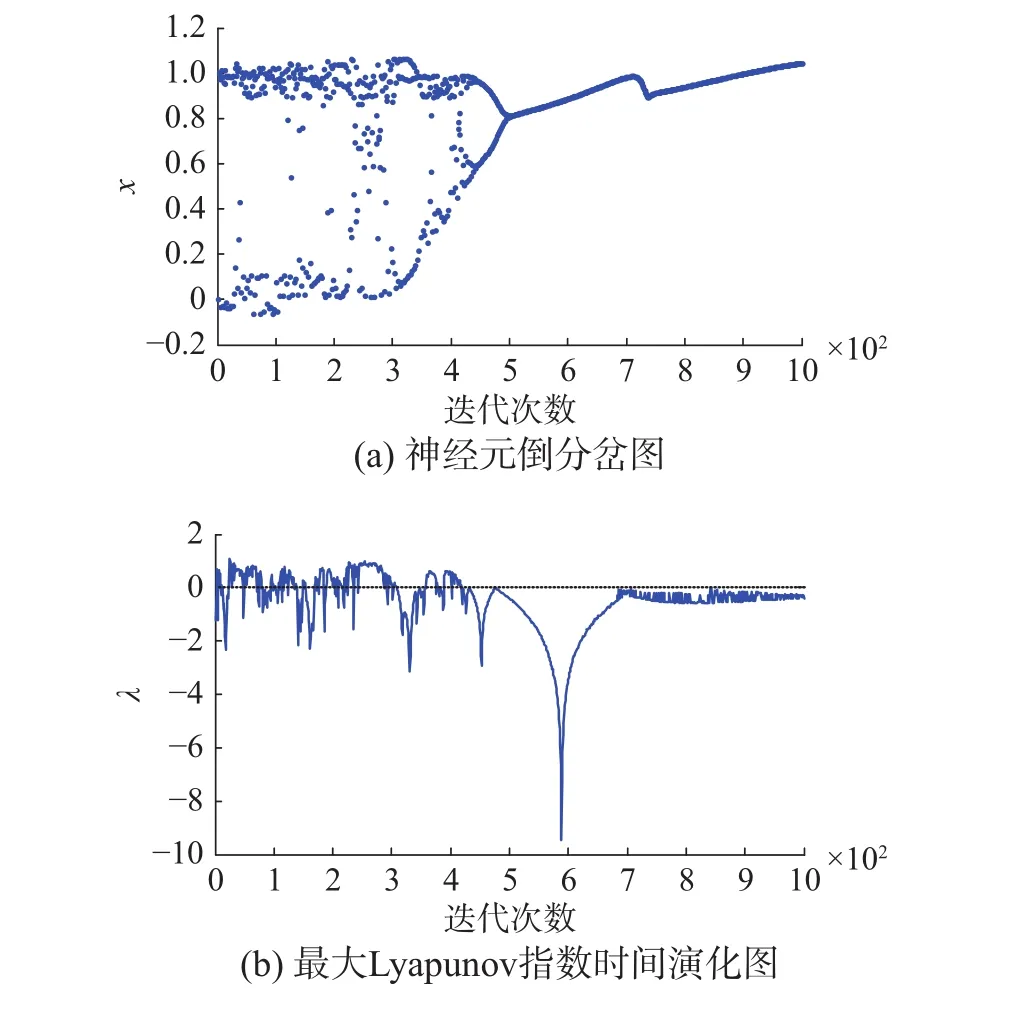
圖 2 帶三角函數擾動(γ=0.02)的FCS神經元倒分岔圖和最大Lyapunov指數圖Fig. 2 The reversed bifurcation and the time evolution of the maximal Lyapunov exponent of the FCS neuron within trigonometric function disturbance(γ=0.02)

當擾動為Morlet小波函數時，選取參數k=1,β=0.004, ε1=0.02, I0=0.65, z(0)=0.9, A(0)=0.6, ε2(0)=0.02, a=6, b=1, c=0.25, ε3=2.5 固定不變時，分別取γ=0.002和γ=0.02時，FCS神經元的倒分岔圖和最大Lyapunov指數時間演化圖如圖3、圖4所示。

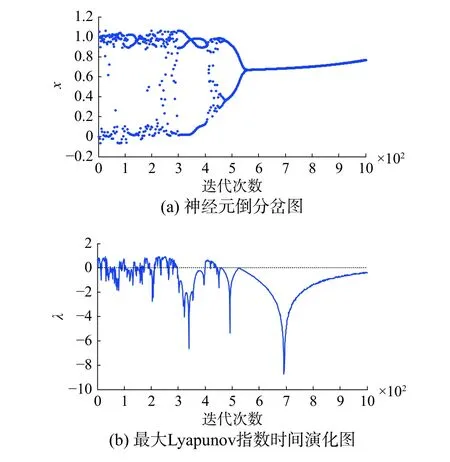
圖 3 帶Morlet小波擾動(γ=0.002)的FCS神經元倒分岔圖和最大Lyapunov指數圖Fig. 3 The reversed bifurcation and the time evolution of the maximal Lyapunov exponent of the FCS neuron within Morlet function disturbance (γ=0.002)

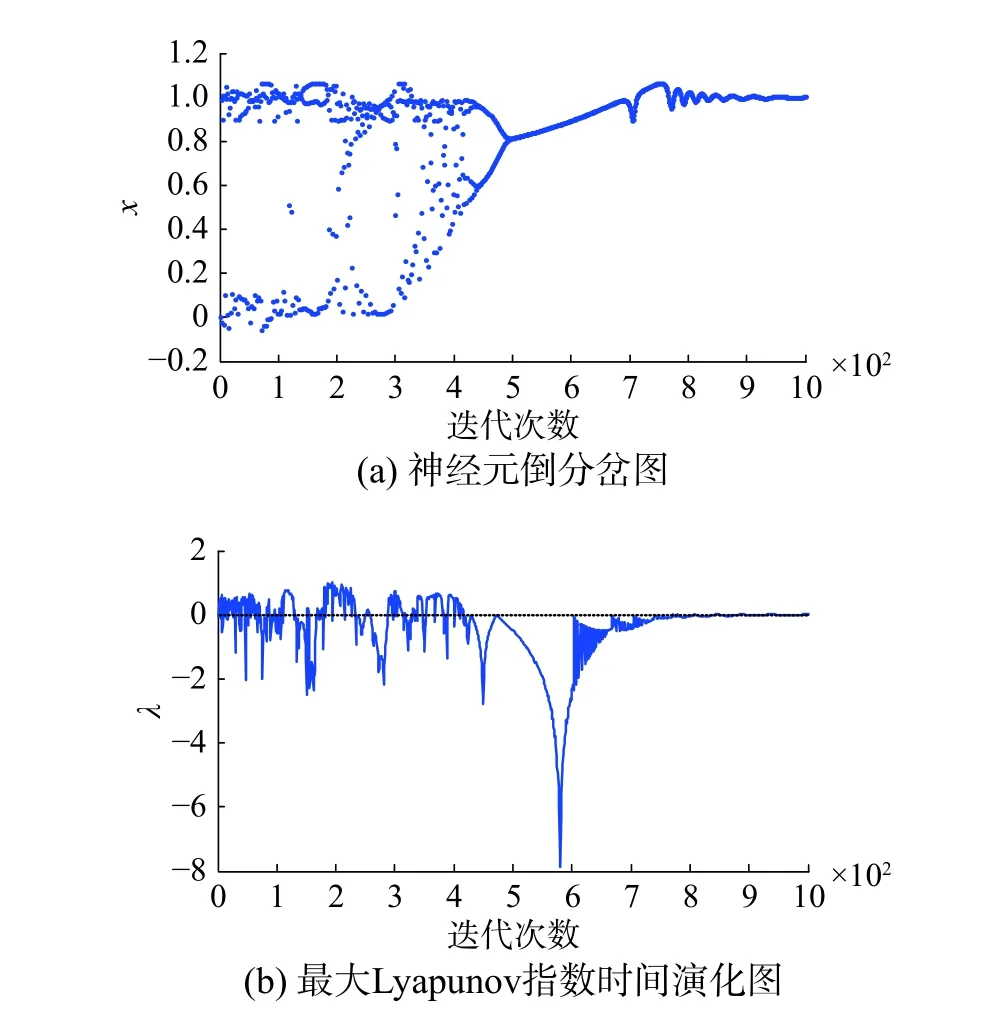
圖 4 帶Morlet小波擾動(γ=0.02)的FCS神經元倒分岔圖和最大Lyapunov指數圖Fig. 4 The reversed bifurcation and the time evolution of the maximal Lyapunov exponent of the FCS neuron within Morlet function disturbance (γ=0.02)

由圖1～4可知，在神經元內部加入三角函數或小波函數擾動項，進行動力學特性對比分析。在擾動系數γ為0.002時，兩類不同的擾動下，神經元的動力學特性都只是發生微小的變動，并沒有發生明顯的改變。在擾動系數γ為0.02時，兩類不同的擾動下，神經元的動力學特性都發生了較明顯的變化，隨著擾動系數的增大，動力學特性變動更加劇烈，動力學演變過程開始受到影響，但是整體的倒分岔特點和混沌程度并沒有受到本質改變，依舊保持原有形態。證明了在一定程度擾動項作用下，FCS混沌神經元模型具有一定魯棒性和抗擾動能力。

2 帶擾動的FCS混沌神經網絡模型

利用上述帶擾動的FCS混沌神經元模型，構建得到了如下帶擾動的FCSCNN模型：

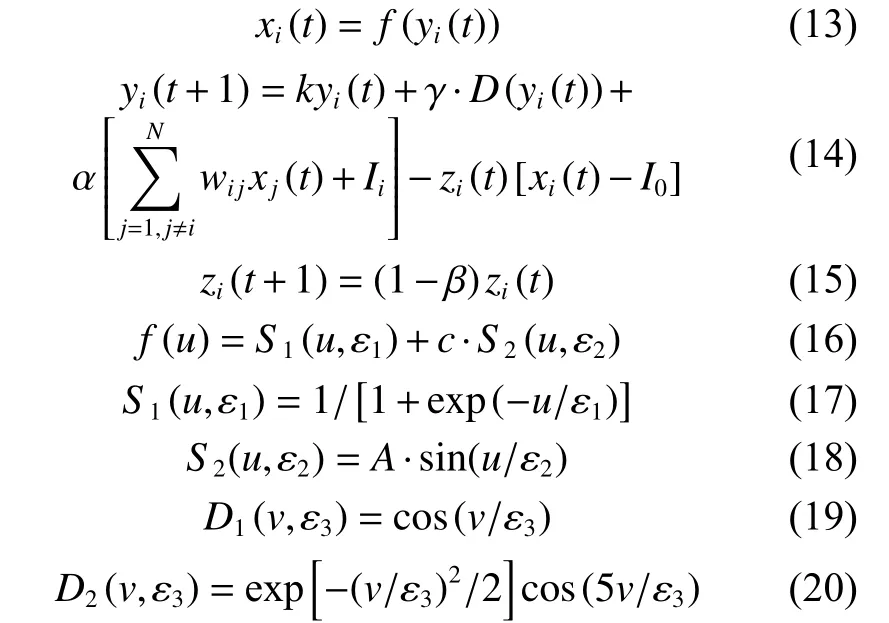
式中：α為正比例參數，wij為神經元i和神經元j間的連接權值(wij=wji, wii=0)，Ii是第i個神經元閾值，其他參數定義同帶擾動的FCS神經元模型。

FCSCNN采用傳統的Hopfield網絡的優化機制[12]。由于自反饋的存在，網絡會表現出混沌特性。在演化初期，選擇合適的網絡參數，并且具有較大的自反饋連接權重初值z(0)，利用混沌的遍歷性和偽隨機性在相空間內按照一定“分形”結構進行“自抑制”的不重復全局搜索，避免陷入局部極小[13]。根據式(15)，隨著退火衰減因子β的作用，z值不斷進行減小，網絡隨之從混沌態經歷倒分岔過程過渡到穩態，直至完全退化為Hopfield網絡，收斂到優化值。FCSCNN模型中動力學特性和優化能力敏感的依賴于網絡參數(k, α, z,β, ε1, ε2, I0)的選擇。k 表征記憶保留或遺忘內部狀態的能力；α表征能量函數對混沌動力學特性的影響，決定著網絡演化和混沌動力的比例；β表征自反饋項的退火速度，決定著混沌特性的退化快慢。參數之間相互影響，需要選擇合理的搭配才能獲得好的優化效果。反之，則無法得到最優解甚至失去優化能力。

當加入擾動后，從圖1～4的神經元動力學特性仿真分析可知，擾動的影響會隨著擾動系數增大而增加，當擾動過大，會改變甚至會完全破壞FCS神經元模型的混沌動力學特性。這將影響FCS模型混沌搜索遍歷性和偽隨機性的動力學特性，不能很好利用自身的自抑制進行全局搜索。因此，要保持良好的尋優能力，除了選擇合適的網絡參數外，還需要控制擾動在適當的范圍內。對于在擾動條件下能否依然較好地解決優化問題，將在不同程度的擾動項作用下，采用FCSCNN模型解決函數優化和組合優化問題，進一步驗證模型的抗擾動能力。

3 帶擾動的FCSCNN模型在優化問題中的應用

根據Hopfield的優化機制有如下規則[14]：

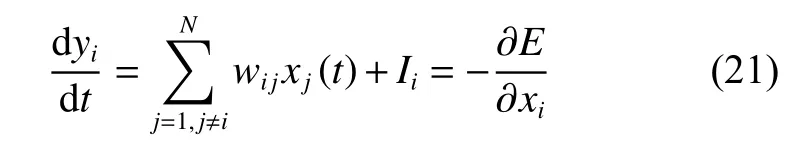
在設置好模型參數后，將問題的目標函數映射為網絡的能量函數，將網絡的動力學演化過程視為目標函數的尋優過程，當網路收斂到穩定點時，對應的神經元輸出即為所要求得優化問題的解。

3.1 在函數優化中的應用

優化函數1：

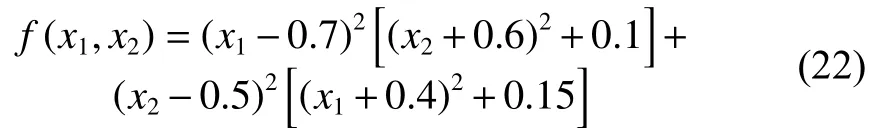
函數f的最小值為0，最小值點為(0.7,0.5)；局部極小點為(0.6,0.4), (0.6,0.5)和(0.7,0.4)。在FCSCNN 模型中，選取參數如下： k=1, α=0.1, β=0.2,ε1=0.08, I0=0.56, z1(0)=z2(0)=0.1, A(0)=0.4, ε2(0)=0.08, a=6, b=1, c=0.25。隨機初始化神經元輸出x1,x2的值，擾動系數γ分別取0.002, 0.02和0.2。對比FCSCNN模型在不同擾動和不同擾動系數下的函數優化能力，進行10次獨立實驗取均值，每次網絡演化50步，實驗結果如表1所示。

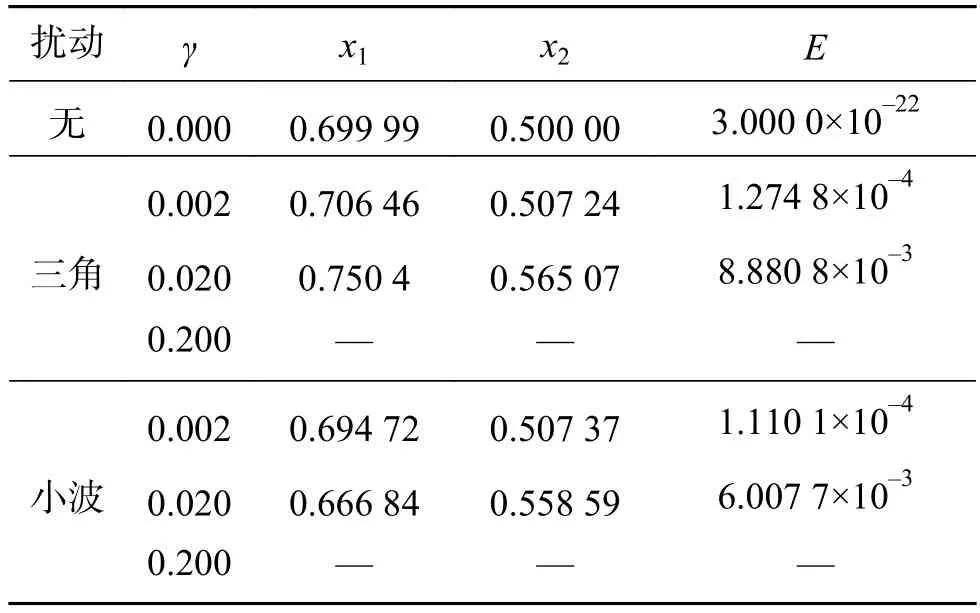
表 1 帶擾動FCSCNN求解函數1優化問題結果Table 1 The optimization results of the FCSCNN with disturbances for function 1

優化函數2：

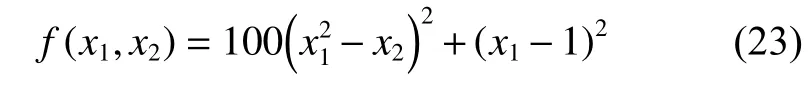
函數f的最小值為0，最小值點為(1, 1)。最優解位于一個平滑、狹長的拋物線形山谷內，函數為優化算法提供的信息比較有限。傳統梯度下降法方向幾乎與最小值的最佳方向垂直，很難辨別搜索方向，查找最優解變得十分困難。在FCSCNN 模型中，選取參數如下：k=1, α=1.0×10–5,β=0.01, ε1=8.0×10–4, I0=0.65, z1(0)=z2(0)=0.8,A(0)=0.4, ε2(0) =0.08, a=6, b=1, c=0.25。隨機初始化神經元輸出x1、x2的值，擾動系數γ分別取0.002、0.02和0.2。對比FCSCNN模型在不同擾動和不同擾動系數下的函數優化能力，進行10次獨立實驗取均值，每次網絡演化5 000步，實驗結果如表2所示：

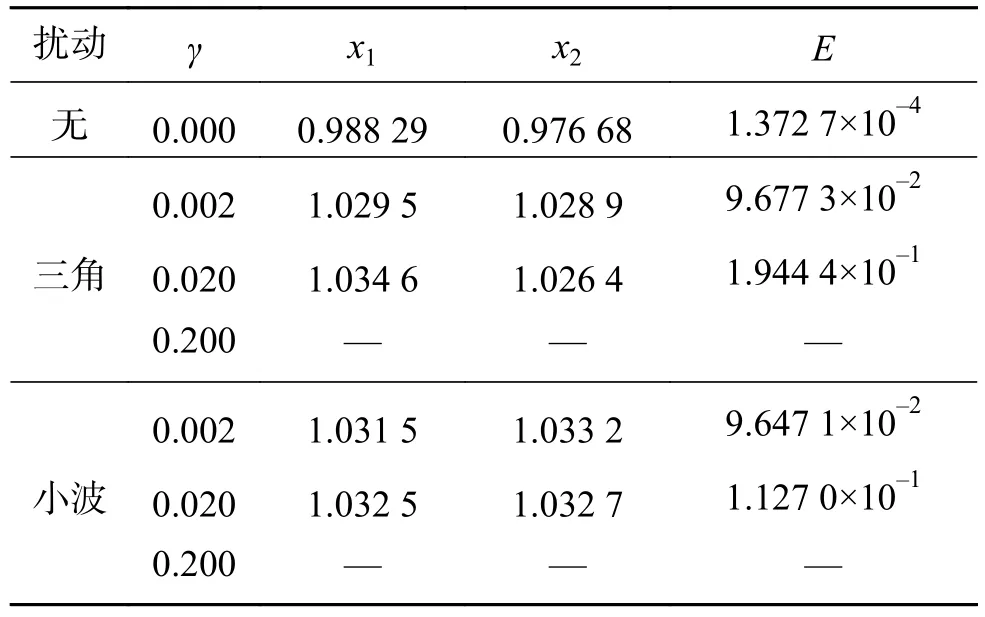
表 2 帶擾動FCSCNN求解函數2優化問題結果Table 2 The optimization results of the FCSCNN with disturbances for function 2

由表1、2仿真實驗可知，當擾動系數γ為0(無擾動)時，FCSCNN模型均具有很好的全局尋優性能，找到了全局最優解；當擾動系數γ為0.002時，模型依然保持了較好的全局搜索能力，能夠比較接近全局最優解；當擾動系數γ為0.02時，模型的尋優能力均出現明顯下降。由于擾動系數γ的增大，擾動項對模型的動力學演化過程和混沌全局性能的影響越大。適當(γ≤0.002)的擾動系數下，網絡可以保持全局尋優能力，當擾動項過大(γ≥0.2)，會影響甚至破壞模型的尋優水平。為了更好地驗證實驗結果，選擇復雜的組合優化問題進一步實驗分析。

3.2 在組合優化中的應用

旅行商(traveling salesman problem, TSP)問題描述如下：

假定有N個城市，給出它們的位置和相互距離，要求尋找一條閉合路徑，每個城市僅且被訪問一次，回到起始城市，要求這條路徑的距離最短。

問題對應的目標函數[14]為

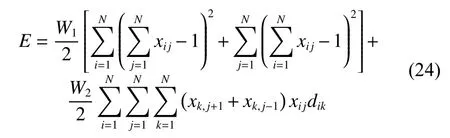
式中：xij為神經元的輸出，它表示城市i于第j個被訪問；W1和W2分別為與約束和關于路徑長度的代價函數對應的耦合系數；dij為城市i和城市j之間的距離。

選取10個城市歸一化后的坐標，取值分別為：(0.400 0, 0.443 9)，(0.243 9, 0.146 3)，(0.170 7,0.229 3)，(0.229 3, 0.716 0)，(0.517 1, 0.941 4)，(0.873 2,0.653 6)，(0.687 8, 0.521 9)，(0.848 8, 0.360 9)，(0.668 3,0.253 6)，(0.619 5, 0.263 4)。該10個城市TSP問題滿足條件最短路徑長度為2.677 6[14]，最優路徑如圖5所示。

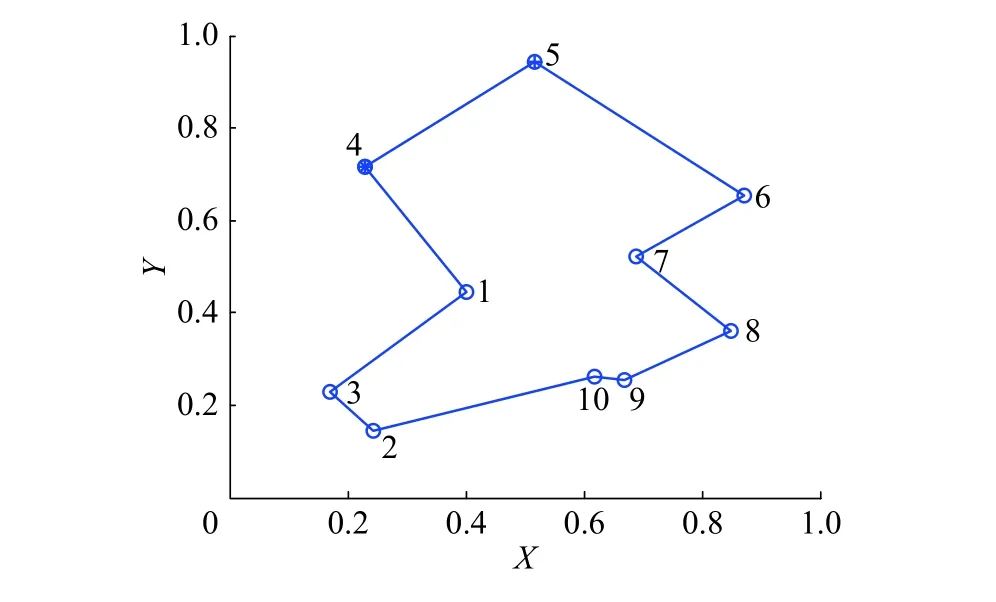
圖 5 10城市TSP問題的最短路徑Fig. 5 The optimal distance of 10 city TSP

在FCSCNN模型中，選取參數如下：k=1,α=0.05, β=0.05, ε1=0.05, I0=0.65, z(0)=0.8, A(0)=0.4,ε2(0)=0.08, a=6, b=1, c=0.25, W1=1, W2=1。隨機初始化神經元輸出xij的值，對比FCSCNN模型在不同擾動和不同擾動系數下的組合優化能力，進行500次獨立實驗，每次網絡演化1 000步，實驗結果如表3所示：

由表3可知，帶擾動的FCSCNN模型在解決10城市旅行商問題時：三角擾動系數γ小于0.005的情況下，合法路徑比率均在95%以上，最優路徑比率均在88%以上；小波擾動系數γ小于0.01的情況下，合法比均在96%以上，最優比均在90%以上。可認為適當的擾動對網絡模型的混沌全局尋優能力影響不大。但是隨著擾動系數的增大，合法比和最優比均呈下降趨勢，擾動項的影響過大時，甚至失去尋優能力。同時，當前的擾動參數下，FCSCNN模型對Morlet小波擾動的魯棒性比三角函數擾動要好。

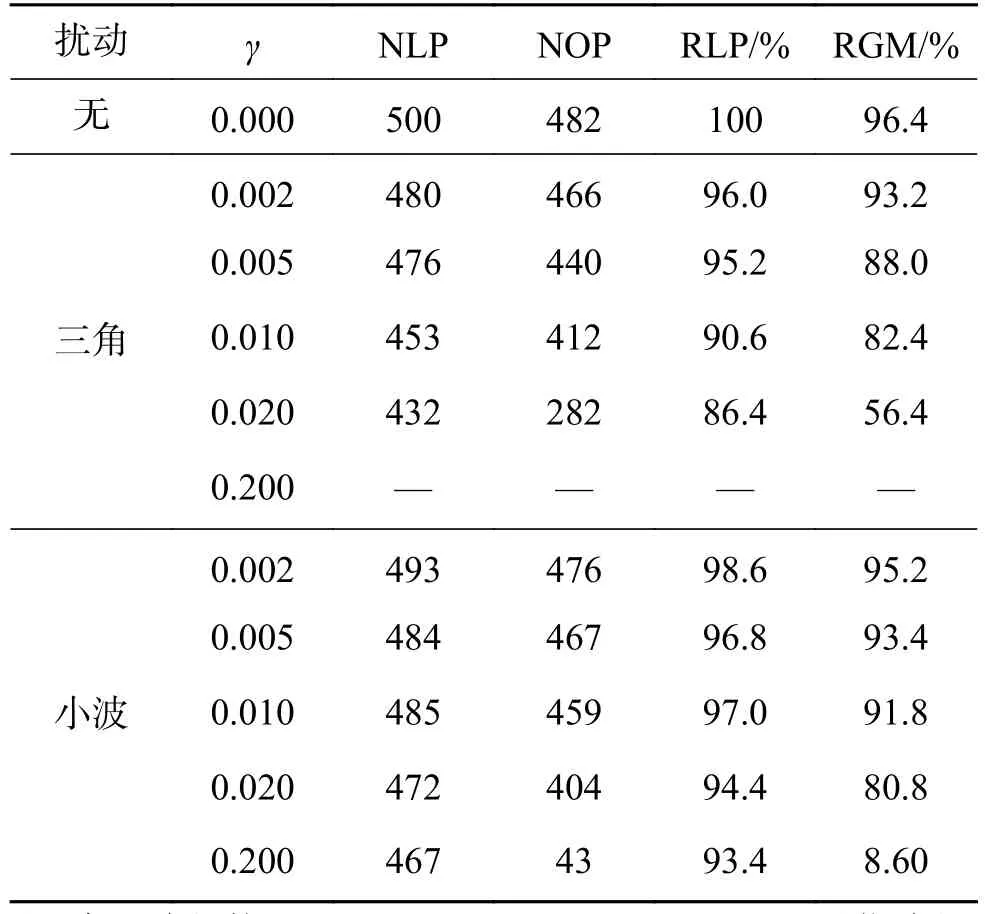
表 3 帶擾動FCSCNN求解10城市TSP問題結果Table 3 The optimization results of the FCSCNN with disturbances for 10 city TSP

選取30個城市歸一化后的坐標，取值分別為：(0.41, 0.94)，(0.37, 0.84)，(0.54, 0.67)，(0.25,0.62)，(0.07, 0.64)，(0.02, 0.99)，(0.68, 0.58)，(0.71,0.44)，(0.54, 0.62)，(0.83, 0.69)，(0.64, 0.60)，(0.18,0.54)，(0.22, 0.60)，(0.83, 0.46)，(0.91, 0.38)，(0.25,0.38)，(0.24, 0.42)，(0.58, 0.69)，(0.71, 0.71)，(0.74,0.78)，(0.87, 0.76)，(0.18, 0.40)，(0.13, 0.40)，(0.82,0.07)，(0.62, 0.32)，(0.58, 0.35)，(0.45, 0.21)，(0.41,0.26)，(0.44, 0.35)，(0.04, 0.50)。該 30 個城市TSP問題滿足條件最短路徑長度為4.237 406[6]，最優路徑如圖6所示。

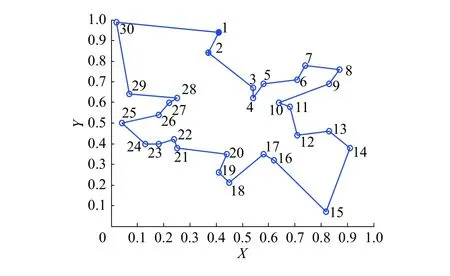
圖 6 30城市TSP歸一化坐標的最短路徑Fig. 6 The optimal distance of 30 city TSP

在FCSCNN模型中，選取參數如下: k=1, α=0.006, β=0.001, ε1=0.04, I0=0.65, z(0)=0.8, A(0)=0.4,ε2(0) =0.08, a=6, b=1, c=0.25,W1=1,W2=1。隨機初始化神經元輸出xij的值，對比FCSCNN模型在不同擾動和不同擾動系數下的組合優化能力，進行200次獨立實驗，每次網絡演化10 000步，實驗結果如表4所示：

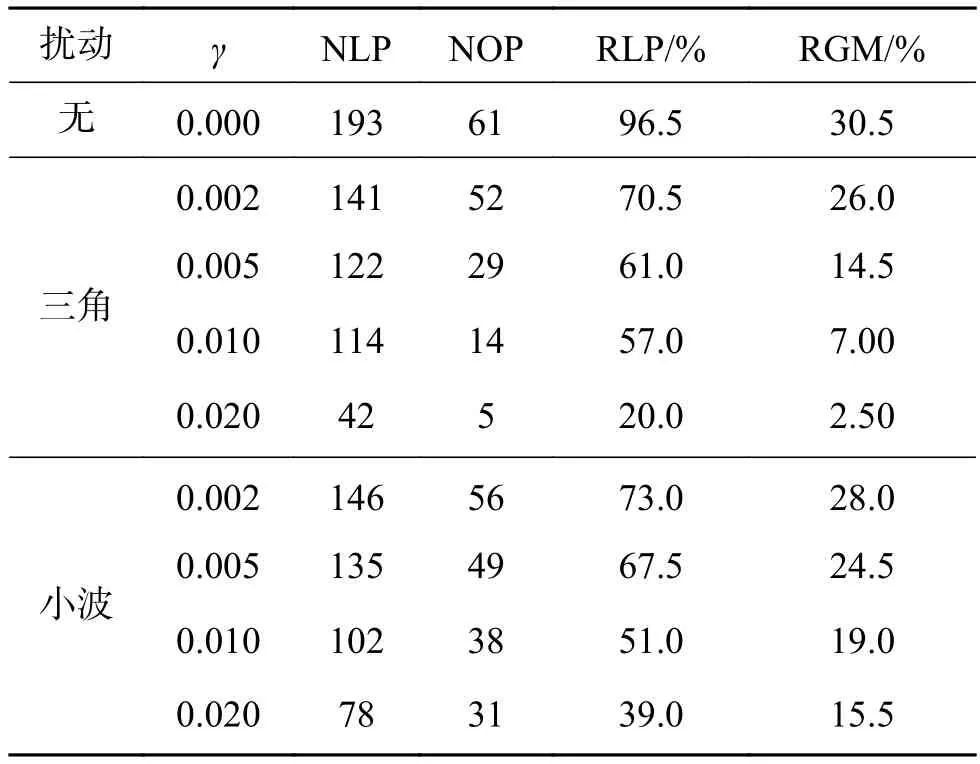
表 4 帶擾動FCSCNN求解30城市TSP問題結果Table 4 The optimization results of the FCSCNN with disturbances for 30 city TSP

由表4可知，30城市的旅行商問題具有更高的復雜度，需要更多的演化步數，這也是TCNN類模型在解決不同問題時需要不同的參數搭配的原因。三角擾動系數γ小于0.002的情況下，合法路徑比率均在70%以上，最優路徑比率均在25%以上；小波擾動系數γ小于0.005的情況下，合法比均在65%以上，最優比均在20%以上。同樣的可認為較小的擾動對網絡模型的混沌全局尋優能力影響不大。在適當擾動強度內，網絡表現出一定的抗擾動能力。

4 結束語

為了驗證的具有非線性激勵函數且比標準的暫態混沌神經元模型具有更豐富混沌動力學特性的新型混沌神經網絡模型—FCSCNN的抗擾動能力，在該模型內部狀態中分別引入三角函數和小波函數擾動項，分析帶擾動的FCS混沌神經元模型的動力學特性。通過神經元倒分岔圖和最大Lyapunov指數圖可知，擾動的引入會影響網絡模型的動力學演化過程，進而會對全局尋優性能產生影響。通過函數優化和組合優化問題的仿真實驗，證實了這種影響會隨著擾動系數的增大而增加，但一定范圍內，FCSCNN模型對三角擾動和Morlet擾動均具有一定魯棒性和抗擾動能力，選取合適的模型參數，依然可以保持較好的全局搜索能力，獲得最優解。