考慮柔性懸架的輪式自行火炮仿真分析

劉昕運，馬吉勝

（軍械工程學院 火炮工程系，河北 石家莊 050003）

1 引言

某型輪式自行火炮是我國自主研制的第一種輪式自行火炮，采用（6×6）驅動模式底盤以及100mm高膛壓滑膛炮[1]。突擊炮是一種用于為步兵提供短距離炮火火力支援的裝甲戰斗車輛。它是一種進攻性武器，要求高機動、大火力地提供迅速和強力的支援。該型武器裝備的作戰模式決定了射擊和行駛產生的振動響應全部經過六個獨立懸架傳遞，在實裝使用過程中，某些長時間工作的自行火炮懸架橫臂上產生疲勞破壞裂紋甚至斷裂失效的現象。因此，分析懸架系統破壞機理以及內部應力應變規律十分必要。目前，針對懸架系統的研究很多，如考慮汽車懸架柔性的整車平順性研究[2]，或者基于懸架剛柔耦合的汽車優化分析等[3]。但是對于輪式自行火炮的懸架剛柔耦合分析極少，大部分文獻均采用剛性圓柱連桿相互連接構成。傳統輪式自行火炮的疲勞強度評估均是利用實車在各種道路路試和射擊實驗，雖然測試較為準確，但是測試時間十分冗長且耗費大量人力和經費。在后期使用時出現問題往往很難發現問題根源，難以修改。隨著計算機軟件的飛速發展，CAE分析技術在此領域取得了相當大的應用成果，節約大量人力財力并能及時在出現問題前后修正實體機構。故運用Solidworks、Adams、Abaqus等軟件建立包含柔性身管和上下橫臂的全炮剛柔耦合動力學模型，對其行駛和射擊過程進行仿真，分析橫臂應力應變規律，以期在后期解決火炮的靜力強度和疲勞強度問題。

2 全炮剛柔耦合模型建立

2.1 火力部分模型

為了射擊時身管能更加準確的模擬后座和復進運動，使用模態綜合法將身管模型簡化為柔體。在Abaqus中建立身管有限元模型，劃分45846個八結點六面體單元并分析模態，取其前50階模態集作為主模態導入Adams中。通過運動副連接耦合節點和炮尾、炮口制退器、搖架，利用Adams函數編輯器、數據樣條曲線、用戶子程序等編寫炮膛合力、復進機力、摩擦力、駐退機力。其中炮膛合力直接由內彈道計算得到的膛壓曲線加載，復進機力和駐退機力分別由式（1）和式（2）加載。

式中：S0—復進機折合高度；Pf0—復進機初力；X—后座位移。

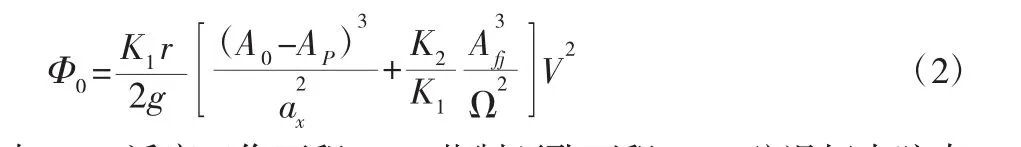
式中：A0—活塞工作面積；Ap—節制環孔面積；Afj—駐退桿內腔直徑面積（復進節制器工作面積）；Ω—支流最小截面積；ax—流液孔面積；K1、K2—主流和支流液壓阻力系數；r—液體重度；V—后坐速度。

2.2 行走部分模型

行走部分可簡化為由車體、獨立懸架、輪胎組成，其中懸架是指車身與車輪之間的一切傳力連接裝置的總稱[4-5]。自行火炮的懸架系統由結構完全相同的六個不等長雙橫臂獨立懸架構成，其結構主要分成A字形下橫臂、單上橫臂、轉向節、液壓減震器、螺旋彈簧。上下橫臂與轉向節直接用球副連接，與車體用轉動副連接，由于不考慮轉向特性，簡化轉向橫拉桿為點面運動約束。減振螺旋彈簧和非線性液壓阻尼器特性由剛度和阻尼曲線決定[1]。

同身管一樣建立懸架上下橫臂有限元模型，采用十節點二次四面體單元劃分網格，其中上橫臂劃分21955個單元，下橫臂劃分68632個單元，橫臂網格劃分，如圖1所示。

圖1 懸架上下橫臂網格劃分Fig.1 Suspension Upper and Lower Arm Meshing

對模型進行模態分析，同樣取前50階模態集，生成帶應力應變信息的模態中性（MNF）文件導入Adams中。

搖架底面和炮尾部分建立接觸，并修改接觸參數以模擬相互撞擊時的緩沖結構。對高低機建模，使用作用在耳軸處的扭簧代替，高低機剛度和阻尼用Y Cai理論[6-8]等效求解接觸剛度并和碟形彈簧剛度串聯而成。

2.3 地面模型

隨機不平路面激勵是影響關鍵位置振動信號的主要因素之一，路面隨機信號只能用各種統計特征量來表征它，可用功率譜密度來表征它的統計功率譜特征，擬合為[8]：

式中：n2、n1—有效頻帶的上下限；n—空間頻率，表示每單位長度變化次數；Gq（no）—參考空間頻率n0下的功率譜值，數值取決于路面的等級。

使用Fourier逆變換法對路面不平度進行重構。該方法是由已知路面功率譜得到對應的一系列離散Fourier變化的模值，再用正態分布隨機序列經Fourier變化后取相位信息作為相角輸入，構造出新的頻域信號，再進行Fourier逆變換就得到所求路面不平度的隨機序列。該方法理論嚴密，所求路面信號與標準路面譜擬合程度最好[9]。

最終組合3個子模型，建立起的全炮剛柔耦合動力學模型，如圖2所示。該模型共由15個剛體和13個柔體組成。

3 仿真計算與分析

3.1 隨機不平路面行駛分析

為比較得出剛柔耦合模型的優點和區別，分別對剛性橫臂懸架和柔性橫臂懸架自行火炮在D級隨機路面上進行行駛仿真分析，2s加速時間，15km/h行駛速度，測量懸架主銷內傾角與輪胎外傾角。主銷內傾角是指鉛垂線和主銷軸線之間的夾角在車輛橫向平面上的投影，車輪跳動時主銷內傾角可提高車輛轉向輕便性，自行火炮主銷內傾角隨車輪上下跳動行程的變化曲線[10]，如圖3所示。車輪外傾角是指車輪胎面與鉛垂線的夾角，其變化曲線，如圖4所示。由計算結果可以看到，剛性懸架系統與柔性懸架系統存在較大差別，這也證明了建立輪式自行火炮剛柔耦合懸架系統的必要性，柔性上下橫臂能夠增加模型的準確性。

圖4 車輪外傾角變化Fig.4 Wheel Camber Angle Changes

3.2 靜止間射擊分析

在進行射擊分析前，需要對射擊模型進行驗證，模型驗證是確定模型準確性的唯一方法。將模型置于平直路面上，各輪制動，身管處于0高低角和0方向角，模擬自行火炮靜止水平射擊過程。將提取的各項仿真數據與相對應的實驗數據進行比較，結果如表1所示。

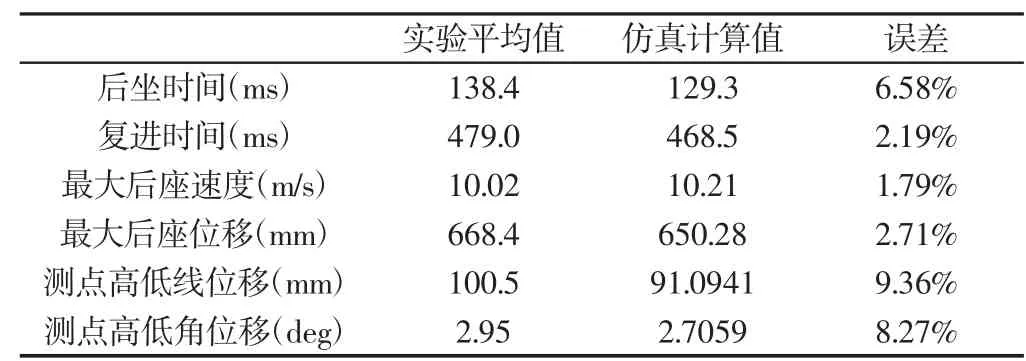
表1 模型驗證Tab.1 Model Validation

對比實驗和仿真數據，誤差均在工程允許范圍內，表明虛擬樣機有一定的準確性和合理性，模型驗證使接下來的射擊仿真計算結果具有可信性。

為比較不同射角工況下懸架的應力狀態，取4不同方向角和3不同高低角共12個射擊角度，分別進行仿真分析并提取懸架最大應力和應變點，由于所有懸架中后輪的工作載荷最大，故選取后輪懸架下橫臂為研究對象，如表2所示。

表2 不同射角下橫臂的應力應變Tab.2 Arm Stress and Strain of Different Angles

計算結果表明，在選取的12射角中，60°方向角20°高低角狀態下的最大應力應變值最大，達到567.272MPa和0.00196MPa。而90°方向角0°高低角狀態下的最大應力應變值最小，只有451.026MPa和0.00148MPa。故在實際射擊中應盡量減少60/20或者30/20射擊角度的工況，這些射擊角度更易加速懸架下橫臂的疲勞破壞。

自行火炮加載炮膛合力后0.3945s時刻的后輪懸架等效應力云圖，如圖5所示。此時刻在下橫臂上達到了最大應力值，如箭頭所指的地方是應力最大的區域，此區域位于下橫臂下表面靠近螺旋彈簧連接的位置，應是懸架系統最易發生破壞失效的地方，這和近年來實體火炮懸架系統產生裂紋區域是吻合的，這也證明了剛柔耦合模型的準確性。如需改進懸架下橫臂的結構強度，可以采取在此區域位置加厚、倒圓角、更換材料等措施。

圖5 懸架橫臂Mises等效應力云圖Fig.5 Suspension Arm Mises Equivalent Stress Cloud

3.3 行進間射擊分析

由于該型輪式自行火炮的作戰模式大多是行駛過程中射擊，故還需對其進行行進間射擊仿真分析。將模型置于平直路面上，選取3種典型射擊角度（30/10、60/20、90/0），持續 2s的加速時間，5s時刻射擊，提取編號1592的最大應力結點處的Mises等效應力隨時間變化的曲線，如圖6所示。

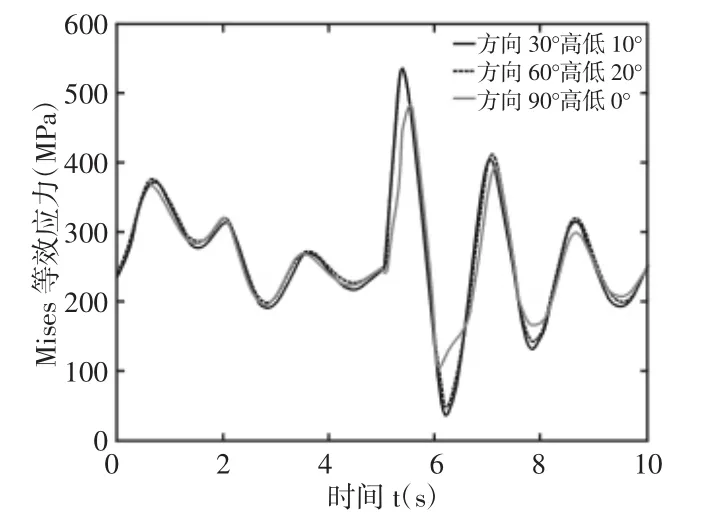
圖6 最大應力點處應力曲線Fig.6 Stress Curve at the Point of Maximum Stress

30/10射擊角度的懸架最大應力值為535.519MPa；60/20射擊角度的懸架最大應力值為539.017MPa；90/0射擊角度的最大應力值為485.938MPa。通過進一步分析12個射擊角度發現，相比于靜止間射擊，方向角為0°30°60°時，行進間射擊懸架下橫臂最大應力值變小，而方向角為90°時，行進間射擊懸架下橫臂最大應力值反而增大。

4 結論

（1）對于輪式自行火炮，經過在隨機路面行駛分析，說明有必要建立包含柔性橫臂的剛柔耦合懸架系統，它能更精確的反映懸架的真實情況，為以后在輪式自行火炮的動力學模型建立提供了參考方法以及理論依據。

（2）對自行火炮模型在靜止狀態進行射擊仿真，結果表明在60°方向角與20°高低角狀態下的最大應力應變值最大，且確定了最大應力值區域位于下橫臂底面靠近螺旋彈簧位置。

（3）對于行進間射擊，低方向角度射擊，行駛會降低后懸架最大應力值；而高方向角度（如垂直行駛方向）射擊，行駛會增大最大應力值。獲得的計算結果直接為傳統靜力破壞和金屬疲勞破壞研究提供參考依據。