RBF神經網絡的主動前輪轉向滑模控制

夏長高，趙維林，任英文

（江蘇大學 汽車與交通工程學院，江蘇 鎮江 212013）

1 引言

汽車的橫向穩定性是評價汽車安全行駛的重要性能，通過主動控制系統來控制汽車行駛的穩定性越來越受重視。這些系統包括直接橫擺力矩控制系統（DYC）、電子穩定控制系統（ESP）、主動前輪轉向系統（AFS）[1]。相對于其他轉向控制系統，主動前輪轉向優勢在于能夠在不調節制動力或驅動力的情況下對汽車穩定性進行控制。主動前輪轉向系統除了保留傳統的轉向系統的基礎上，在轉向盤和齒輪齒條轉向機之間增加了一套雙行星齒輪機構，助力轉向電機通過行星齒輪產生附加的轉向角，共同作用產生總的輸出轉角[2]。主動前輪轉向的控制方法主要有PID控制[3]、模糊邏輯控制[4-5]、模型預測控制（MPC）[6]、滑模控制（SMC）[7-8]、遺傳算法優化的BP網絡控制[9]。

滑模控制作為變結構控制的一種，具有對參數變化及外部擾動不敏感的特點，已成為非線性控制領域關注的熱點之一[10]。論文[7-8]利用滑模控制理論對主動轉向系統進行了控制，通過仿真表明滑模控制能夠有效的控制汽車的穩定性。但滑模控制中的滑模增益使系統產生高頻抖振，如何削弱高頻“抖振”現象卻并未提及。

由于RBF神經網絡能具有較強的自適應和容錯性能[11-12]。鑒于此，提出基于RBF神經網絡的主動前輪轉向滑模控制（RBFSMC）策略。利用RBF神經網絡優化切換增益的方法，削弱滑模控制帶來的“抖振”現象。運用CarSim搭建汽車整車模型，在Matlab/Simulink設計RBF神經網絡滑模控制策略。并進行轉向階躍和雙移線這兩種典型工況仿真，將無控制、SMC控制、RBFSMC控制這三種控制的結果進行對比。來驗證RBF-SMC控制策略對汽車操縱穩定性改善效果。

2 主動前輪轉向系統描述

主動前輪轉向系統包括傳統的齒輪齒條式轉向系統、雙行星齒輪機構、調整電機、ECU以及各種傳感器。如圖1所示。

圖1 主動前輪轉向系統原理圖Fig.1 Active Front Steering System Diagram

雙行星齒輪機構有兩個輸入端：其一是駕駛員通過驅動轉向盤帶動太陽輪旋轉，其二是調整電機通過蝸輪蝸桿帶動行星齒輪旋轉[13]。因此，整個系統的輸入轉向角度δg（t）是轉向盤的輸入角度δh（t）與調整電機的輸入角度δm（t）的疊加。它們的關系滿足于：

3 RBF-SMC控制器設計

為了削弱傳統的主動轉向滑模控制帶來的“抖振”現象，設計了RBF-SMC控制器。根據實際橫擺角速度與理想值建立滑模面，再通過RBF神經網絡調節切換增益。

3.1 參考模型

一般情況下，駕駛員希望車輛轉向隨著方向盤的輸入而呈線性變化，從而獲得較好的操縱性能，所以汽車穩定性目標的參考值一般由二自由度模型式（3）確定。

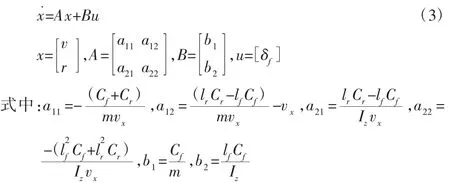
式中：m—整車質量，kg；Cf、Cr—前后車輪的側偏剛度，N/rad；δf—前輪轉角，rad；Iz—汽車繞 z軸的轉動慣量，kg·m；v—側向速度，km/h；r—橫擺角速度，rad/s；lf、lr—質心到前后軸的距離，m。

而實際行駛的車輛由于前后輪的側偏剛度都是隨時間變化的。可用式（4）表示：

式中：ΔCf、ΔCr—前后輪側偏剛度不確定量。

式（4）代入（3）中可得：

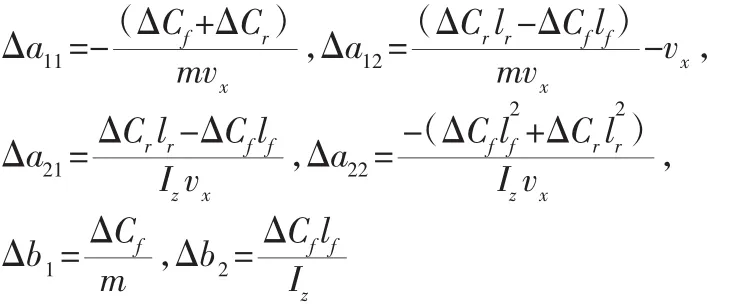
取系統的不確定量為：f（x，t）=ΔAx+ΔBu=Bd（x，t）（6）

根據式（5）和式（6）得：x˙=Ax+Bu+Bd（x，t） （7）

以橫擺角速度r為控制目標，即有：

汽車行駛達到穩定，即v˙y=0，r˙=0。通過變形消去 vy，同時考慮路面附著條件，則理想橫擺角速度為：

3.2 滑模面設計

滑模變結構能夠讓系統結構隨時間變化，迫使系統最終穩定在滑模面附近，再通過切換函數是系統收斂于滑模面。主動前輪轉向系統的控制目的是使汽車橫擺角速度r迅速、準確地跟蹤當前設定值的任意變化，為此，定義滑模控制的切換函數為：

式中：λ—正加權系數。

令S˙=0，為了使系統在有擾動情況下還能收斂于滑模面，則滑模控制律為：

式中：Kr—滑模切換增益。

所以該滑模控制器的輸出為：

3.3 基于RBF神經網絡的切換增益設計

由于外部擾動及系統參數具有時變性，固定切換增益難以獲得最優的控制性能，不能夠有效的削弱“抖振”現象。提出基于RBF神經網絡的優化增益的控制方法。RBF神經網絡主動前輪轉向控制實現對滑模切換增益的調節，設計了RBF神經網絡，該RBF神經網絡具有兩個輸出量、六個隱含層節點、一個輸出量。RBF神經網絡結構，如圖2所示。

圖2 主動前輪控制的RBF神經網絡結構Fig.2 The Structure of RBF Neural Network for Active Front Steering

RBF神經網絡的輸入為X=［S S˙］。則RBF神經網絡的輸出為：

RBF神經網絡的徑向基向量。徑向基向量hi選擇高斯基函數，即：

式中：ci=［c1，c2，c3］—網絡節點的中心向量；bi=［b1，b2，b3］—網絡的基寬向量。

根據滑模控制原理，控制目標選為SS˙→0，所以RBF神經滑模的權值調整指標為：

E=S（t）S˙（t），則

式中：η＞0

式中：b—系統的輸入參數。

由式（15）和式（16）可得

式中：γ—系統的學習速率，γ=η·b。

所以RBF神經網絡權值調節算法為：

4 CarSim/Simulink聯合仿真平臺搭建

針對提出的RBF神經網絡滑模控制策略，運用CarSim/Simulink聯合仿真平臺進行驗證。CarSim軟件能夠提供高精度的車輛動力學模型，對各種復雜情況下具有較強程度的擬合；Matlab/Simulink中可以設計復雜的控制器以及各種動力學仿真分析軟件的聯合仿真。此次研究搭建的聯合仿真平臺，如圖3所示。CarSim仿真軟件提供汽車的動力學模型，Simulink中搭建RBF神經滑模控制器控制策略，并把控制結果的輸出傳給CarSim的汽車模型中，實現聯合仿真模型的搭建。

圖3 CarSim/Simulink聯合仿真平臺Fig.3 The Co-simulation Platform of CarSim/Simulink

5 仿真驗證與分析

為了驗證RBF神經網絡滑模控制對主動轉向系統的控制效果，選擇轉向角階躍輸入和雙移線兩種典型工況進行仿真，驗證所設計的控制器的控制效果。

5.1 階躍轉向工況

車速為90km/h，路面附著系數μ為0.85的干瀝青路面，轉向盤的最大轉角為60°，階躍時間為1s。仿真試驗結果，如圖4～圖7所示。試驗數據，如表1所示。

從圖4可以看出：設計的RBF神經網絡的滑模控制器相對于傳統的滑模控制器能夠有效的抑制“抖振”現象；從圖5和圖6以及表1中可以看出，車輛在RBF神經網絡的滑模控制器下能夠有效減少橫擺角速度的峰值，相對于傳統的滑模控制器能夠使側向加速度和橫擺角速度的減少了23.68%和23.81%，而RBF神經網絡滑模控制器能夠減少25.12%和25.26%。提高了在轉向階躍工況的控制效果。

圖4 SMC控制量曲線Fig.4 SMC Control Value Curve

圖5 側向加速度曲線Fig.5 The Lateral Acceleration Curve

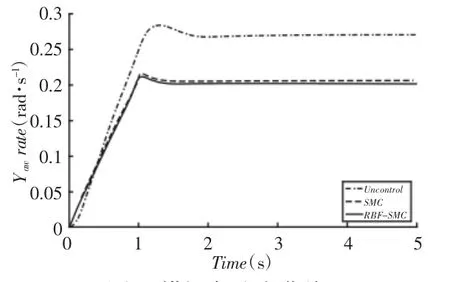
圖6 橫擺角速度曲線Fig.6 The Yaw RateCurve

表1 階躍轉向工況仿真試驗數據Tab.1 The Simulation Test Data of Step Response

5.2 雙移線工況

仿真工況描述：仿真路面設為附著系數為0.85的干瀝青路面，車輛以90km/h的速度行駛，在試驗開始后以180°/s的速度正向轉動方向盤至180°，接著反向轉動360°。仿真試驗結果，如圖7、圖8、圖9所示，試驗數據，如表2所示。

從圖7中可以看出：在雙移線仿真試驗中，控制量S在傳統的滑模控制中出現了明顯的“抖振”現象，這樣會嚴重的損害系統的控制效果，而RBF神經網絡滑模控制有效削弱了“抖振”現象；從圖8、圖9和表2中可以看出，RBF神經滑模控制能更好的減少側向加速度和橫擺角速度的峰值，相對于傳統的滑模控制器能夠使側向加速度和橫擺角速度減少6.63%和5.99%，而RBF神經網絡滑模控制器能夠減少10.62%和10.38%。提高了對汽車在雙移線工況下的控制效果。

圖7 SMC控制量曲線Fig.7 SMC Control Value Curve

圖8 側向加速度曲線Fig.8 The Lateral Acceleration Curve

圖9 橫擺角速度曲線Fig.9 The Yaw Rate Curve

表2 雙移線工況仿真試驗數據Tab.2 The Simulation Test Data of Double Lane Change

6 結論

建立了主動前輪轉向的數學模型以及前后輪側偏剛度不確定的二自由度整車模型。通過對傳統滑模控制出現的“抖振”現象的研究，設計基于RBF神經網絡的主動前輪轉向滑模控制器。搭建了CarSim和Simulink聯合仿真平臺，在階躍轉向和雙移線兩種典型的工況下進行仿真試驗。從仿真實驗的數據可以得出：

（1）相對于傳統滑模控制的主動前輪轉向系統，基于RBF神經網絡優化切換增益的方法能夠有效抑制“抖振”現象，能夠對前輪轉角較平穩的調節，減少對元件的損害。

（2）基于RBF神經網絡滑模的控制器相對于傳統的滑模控制器，能夠使橫擺角速度和質心側偏角得到相對改善，從而提高了車輛的操縱穩定性。