高阻尼人-結構系統的共振頻率研究

傅 豪 葉 茂 徐梅玲

(廣州大學/廣州大學-淡江大學工程災害與控制聯合研究中心,廣州 511400 )

0 引 言

隨著結構材料、工藝的不斷更新,結構呈現出了跨度越來越大、整體越來越柔的特點,使得結構自振頻率越來越低,人群的荷載作用致使結構更容易被誘發振動,此種現象在大跨度結構中尤為突出。2010年,山西藏山舉行的某大型活動中,搭建的臨時看臺突然坍塌事件,導致數名人員受傷[1],孫昊[2]提出,在靜止站立的單個人或人群會改變結構的動力學特性,所以人體自身對于結構有著重要的影響。因此,實際工程中考慮人體對結構的影響是必要的。目前,關于人體-結構相互作用的研究主要分為兩方面:人體生物動力學和結構動力學[3]。在人體生物動力學中,Y.Matsumoto和Griffin[3]主要通過研究人體表觀質量,分析人體靜止站立的自然頻率:其中,人體靜止站立時水平方向的自振頻率為0.5 Hz左右[4],豎直方向為5～6 Hz[5],并結合數學模型進行模擬[5]。在土木工程領域,早期研究人員將人體簡化為附加質量作用于結構上,導致結構自振頻率減小,阻尼不變,這與實際測結構不相符。直到1987年,Foschi和Gupta基于體系阻尼增加的現象,提出了人體應當被簡化為一個有阻尼的動力模型[7]。再后來,Eills和Ji將人體簡化為單自由度質量-彈簧-阻尼體系(SDOF)[8]和考慮質量器單自由度及兩自由度質量-彈簧-阻尼體系[9-10]。E.Shahabpoor等[11]同樣采用單自由度體系分體人體在結構上行走時對結構的影響。國內這方面的研究較少,楊予等[11]將人體站立豎直方向振動等效為單自由度模型進行參數研究,王海等[13]采用SDOF研究人體與梁相互作用的動力學模型以及其耦合作用時體系的響應。

已有的研究成果,有將人體簡化為單自由度質量-彈簧體系,這種模型的缺點是無法解釋人-結構相互作用體系的第二階共振頻率低于結構頻率的特性[8]。同時,以往研究人員在探討人-結構系統的動力特性時,采用系統的固有頻率來代替共振頻率進行討論[13],這種簡化對于低阻力的系統是能夠接受的,但人體的高阻尼特性,使得這種簡化在分析人-結構系統動力特性時存在一定的問題。基于以上討論,本文將人體簡化為兩自由度質量-彈簧-阻尼系統[6],并結合Griffin[4]關于兩自由度人體模型參數,提出了三自由度質量-彈簧-阻尼系統的人-結構系統模型,并以共振頻率為研究對象,探討人-結構系統的動力特性。

1 人-結構系統模型

高阻尼三自由度人-結構系統模型如圖1所示,其中上面兩自由度用于模擬人體。其中兩自由度人體模型對應的模態質量為M1、M2,模態剛度為K1、K2,模態阻尼為C1、C2。該三自由度模型的最下面一個自由度用于模擬結構,MS、KS、CS分別為結構的模態質量、模態剛度、模態阻尼。采用x1、x2、xs分別表示三自由度M1、M2、MS的位移。F為對結構施加簡諧荷載(Ps(t)=P0sinωt)的激振器,S為拾振器,用于采集結構在激振器作用下的加速度和位移,并計算共振頻率。

2 人-結構系統共振頻率

圖1所示三自由度質量-彈簧-阻尼模型的運動方程下:

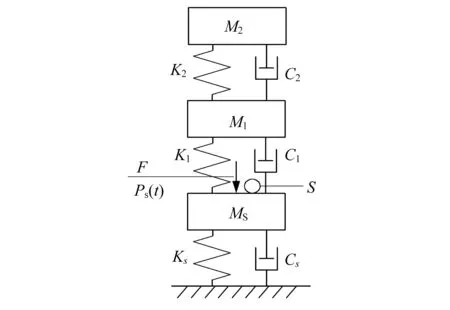
圖1 人-結構體系模型Fig.1 Models of human-structure interaction

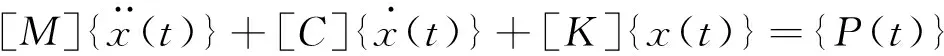
(1)

式中:

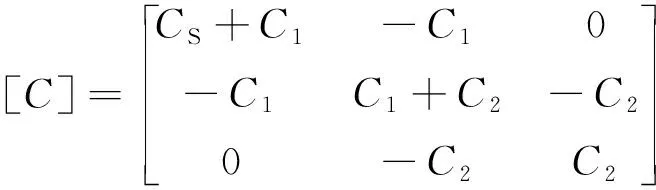
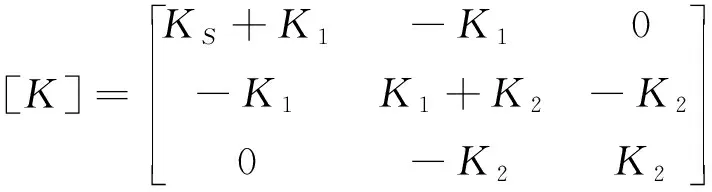
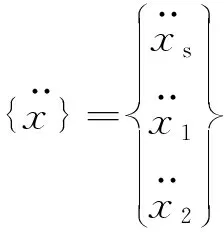
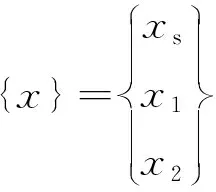
對式(1)進行傅里葉變換,變形得:

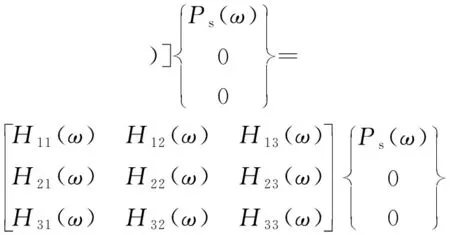
式中:

(2)

其中:

Z(ω)=[-MSω2+i(CS+C1)ω+(KS+K1)][-M2ω2+i(C2+C1)ω+(K2+K1)][-M2ω2+iC2ω+K2]-

(iC1ω+K1)2[-M2ω2+iC2ω+K2]-(iC2ω+K2)2[-MSω2+i(CS+C1)ω+(KS+K1)]

通過式(1)和式(2),可得結構加速的頻率響應函數:

ω2H11(ω)=

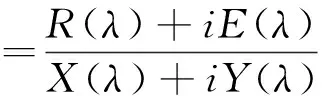
(3)

其中:

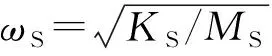
式(3)加速度頻響函數的極大值點為系統的共振點,對該式求導,如下式所示:

(4)

要使式(3)的計算結果為系統的共振點,計算結果應滿足式下式:

(5)

由式(4)知影響體系共振頻率的因素有8個:α,α1,β1,β2,ξ1,ξ2,ξS和MS,其中MS為常數對方程(4)的根無影響,不影響體系的共振頻率。在本文中,結構的阻尼比取ξS=0.01,于是主要影響體系響應共振頻率的因子為6個,即:質量比α,α1,阻尼比ξ1,ξ2,頻率比β1,β2(取β2=εβ1,故分析ε即可)。

3 人體模型參數

曼徹斯特大學JI教授團隊[9]發表了關于豎直方向人-結構相互作用實驗研究成果,測得單人(66.4 kg)站立于平臺、4人(276.7 kg)站立于平臺時結構響應的加速度如圖3所示。其中該試驗豎直固有頻率為2.88 Hz,模態質量為180 kg,低阻尼體系。

根據人體生物學,Griffin等[6]關于人體豎直方向兩自由度模型(圖2)的參數,計算得到質量比為α=1.46,阻尼比為ξ1=0.37、ξ2=0.4,圓頻率為ω1=87.34 rad/s、ω2=37.45 rad/s。于是,頻率比β1=4.83、β2=2.07,質量比為α=1.46,JI的試驗中,單人站立時有α1=0.21,4人時有α1=0.89。

將上述Griffin中人體模型參數,帶入體系加速度頻響函數式(3)中,并通過MATLAB繪制圖形如圖4所示。圖中縱坐標為體系的加速度頻響譜值A11(λ),橫坐標為體系振動頻率與結構固有頻率的比值λ。將圖4中模擬的結果與圖3中進行對比得:單人站立平臺時(圖4(a)),試驗中出現了一個比原結構頻率低的共振頻率,與試驗的結果相符合(圖3(a));4人站立于平臺時,將模擬結果(圖4(b))與實驗結果(圖3(b))對比知:圖中出現了與試驗結果相近的兩個頻率,這也與試驗現象符合。但是,在圖4(a)中,Griffin模型計算得到的結果在0～15 Hz范圍內處還有出現一個共振值(5.429 Hz),但是Ji的實驗中并沒有識別這個結果,而圖4(b)則展現出結果與實驗結果非常相符,這應該與人-結構耦合程度(4人站立時,人-結構耦合更加明顯)和測試分析技術的靈敏度有關。

上述與試驗結果的對比分析表明,本文提出的高阻尼人-結構三自由度模型能較好地描述人-結構相互作用。為此,本文將以本模型為基礎,對高阻尼人-結構三自由度模型進行系統分析,探討人與結構間的質量比、頻率比、阻尼比對人-結構體系共振頻率的影響規律。

圖2 兩自由度人體模型模型(Griffin )Fig.2 TDOF of human body model (Griffin )

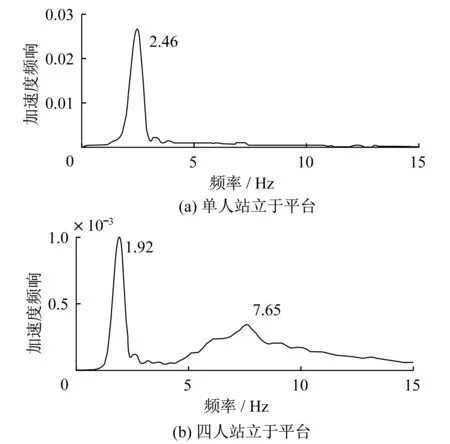
圖3 加速度響應譜圖(JI)Fig.3 Spectral response for acceleration (JI)

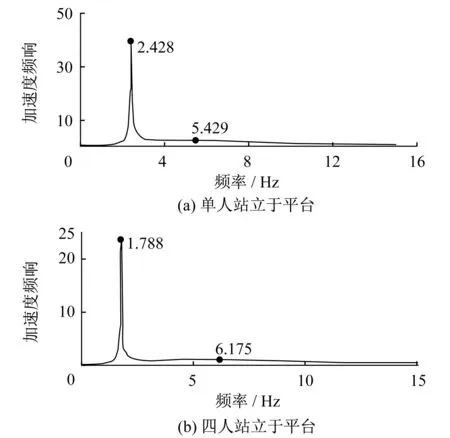
圖4 模擬的加速度響應譜圖(式(5))Fig.4 Spectral response for acceleration (Equation (5))

4 數值分析

將人-結構系統簡化為三自由度質量-彈簧-阻尼模型,通過理論分析得到結構響應加速度頻響函數解析式(4),可知影響體系共振頻率主要因子有:兩自由度人體模型模態質量比(α)、阻尼比(ξH1、ξH2),以及人與結構的模態質量比(α1、α2)、頻率比(β1、β2)等。通過結合Griffin兩自由度人體模型參數,分別對α1,β1,ξ1,ξ2進行定值數值分析。如秦敬偉等[15]展開單人一簡支梁系統靜態耦合下人梁質量比、頻率比、阻尼比、人體位置等參數對系統豎向振動特性影響的理論研究中,分別獨立的來研究對體系共振頻率的影響,在研究其中一個參數,如頻率比時,其他參數為定值,通過其數值分析導出的共振頻率影響圖來判斷對結構整體共振頻率的影響。則本文其結構模態質量比α1,頻率比β1,阻尼比ξ1、ξ2四個參數,也是分別獨立討論,研究其對體系共振頻率的影響。

結構的阻尼比取ξS=0.01,人體阻尼比為0.1～0.5[5,16]。

圖5中為研究各個影響因子對體系共振頻率的影響情況,縱軸為結構響應的加速度頻率譜值,橫軸為體系振動頻率與結構基頻的比值λ,表2為對應圖中極大值對應的λ值。

圖5(a)及表2(a)為人體與結構頻率比β1對體系共振頻率的影響情況;其中,β1分別取0.1、

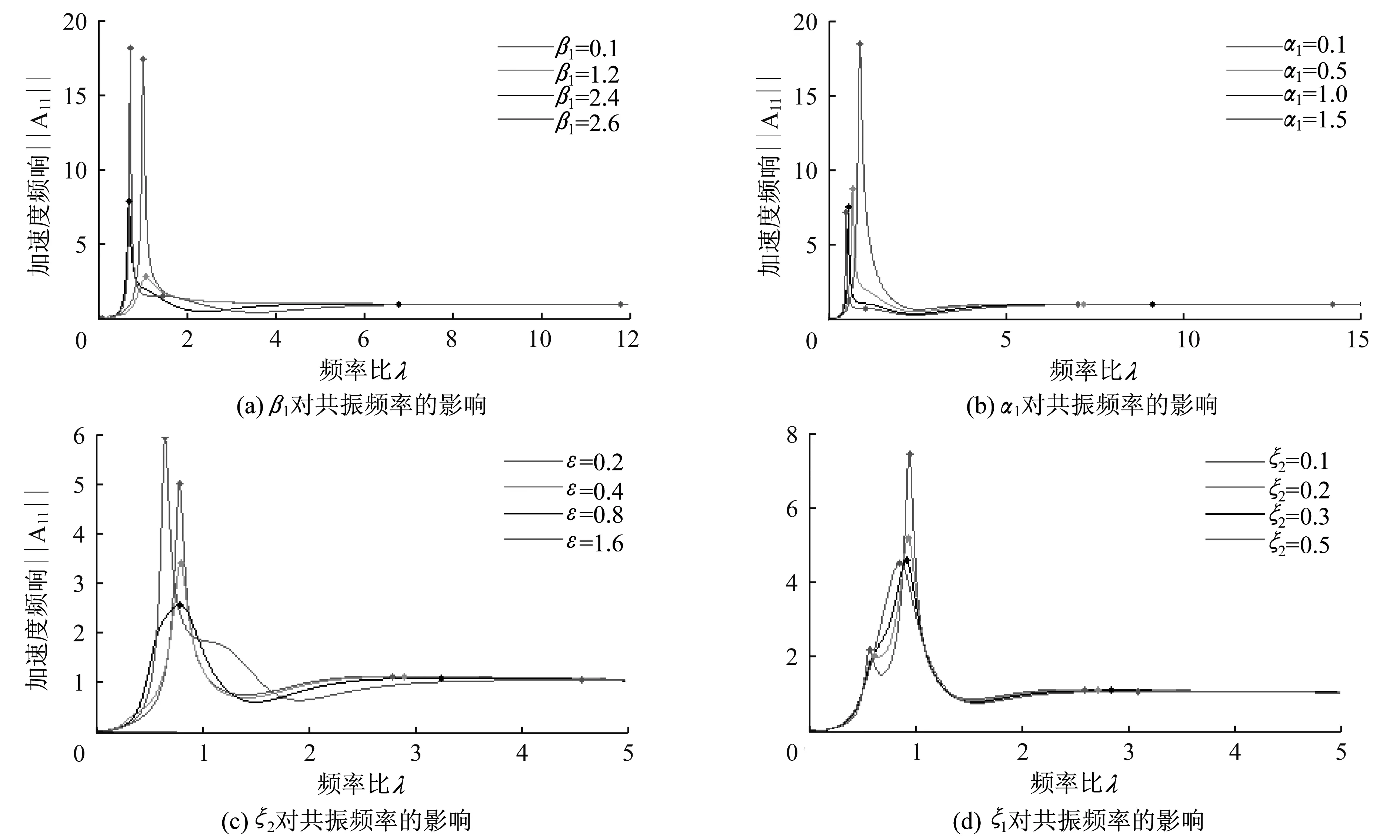
圖5 各種參數對體系共振頻率的影響圖Fig.5 Effects of parameters on presence of resonance frequencies

表2各種參數對體系共振頻率的影響

Table 2Effects of parameters on resonance frequencies

1.2、2.4、3.6,α=1.46,α1=0.25,ξ1=0.37,ξ2=0.4,ε=0.429。在此參數數取值情況下:隨β1的增加,體系的共振頻率成增大的趨勢;同時,針對頻率比β1,取(0,6)間隔為0.01的數值逐項計算知,當β1的取值在[3.47,6.00]內時,體系出現三個共振頻率;取值在[0.44,0.87]內時,出現一個共振頻率,其他情況均出現兩個共振頻率。

圖5(b)及表2(b)為人體模型m1與結構模態質量比α1對體系共振頻率的影響情況;α1取值為0.1、0.5、1.0、1.5,α=1.46,β1=2.5,ξ1=0.37,ξ2=0.4,ε=0.4。由于自由度m1占人體模型總質量的0.574倍,故人體模型總質量與結構的比值為α1/0.574。此參數數取值情況下:體系第一個共振頻率隨質量比α1的增加而成減小的趨勢;同時,針對質量比α1,取(0,6)間隔為0.01的數值逐項計算知,當α1的取值在[1.41,1.90]內時(人體模型總質量與結構的比值取值為[2.46,3.31]),體系出現三個共振頻率,其他情況均出現兩個共振頻率。

圖5(c)及表2(c)和圖5(d)及表2(d)分別表示人體阻尼比ξ1、ξ2對結構響應加速度響應情況的影響,其中α=1.46、α1=0.25、β1=1.5、ε=0.429:在ξ2=0.4時,阻尼比ξ1對體系第一階共振頻率的影響甚小;隨著ξ1的增加,第二個共振頻率呈增大的趨勢;在ξ1=0.37時,隨著ξ2的增加,第二個共振頻率呈減小的趨勢,且當ξ2取值較小時出現三個共振頻率,且前兩階頻率均小于原結構固有頻率。同時,針對阻尼比ξ2,取(0,0.5)間隔為0.001的數值逐項計算知,當ξ2的取值在(0,0.208]內時,體系出現三個共振頻率,其他情況均出現兩個共振頻率;同樣范圍內,分析ξ1的影響時,體系只出現兩個共振頻率。于是,可認為阻尼比ξ2對共振頻率的影響比ξ1的影響更明顯。

通過對每個影響因子,進行逐項數值分析可知:當采用Griffin的人體模型參數分析時,頻率比β1對人-結構相互作用體系出現一個共振頻率的影響,比質量比α1的影響更大;當質量比頻率比取特定的值時,體系會出現一個、兩個、三個共振頻率。針對人-結構相互作用的三自由度模型分析。

5 結 論

(1) 本文針對人體的高阻尼特性,基于人體兩自由度模型,提出了高阻尼人-結構相互作用系統的三自由度質量-彈簧-阻尼模型,推導得到結構響應的加速度頻響譜的解析式。

(2) 通過模型與實驗結果對比,Griffin人體模型參數能模擬出試驗現象,能基本反映人-結構系統的動力特性。

(3) 在本文中,根據式(4)可知,主要影響體系響應共振頻率的因子為:質量比α、α1,阻尼比ξ1、ξ2=,頻率比β1、β2,本文通過結合Griffin兩自由度人體模型參數,分別對質量比之一α1,頻率比之一β1和ξ1、ξ2=進行定值數值分析。

(4)最后,對高阻尼人-結構三自由度模型進行了系統數值分析,分別獨立的分析和研究了各個參數對體系共振頻率的影響規律,表明:采用Griffin模型參數分析時,由于高阻尼的存在,只有當模態質量比α1、α2和頻率比β1、β2取特定值時,才可能出現三個共振頻率;同時,也解釋了出現一個共振頻率、兩個共振頻率以及前兩階頻率均小于原結構固有頻率的情況。在人-結構相互作用的的體系中,通過分析發現,若人-結構相互作用體系出現一個共振頻率,頻率比β1比質量比α1的影響更大;當質量比、頻率比取特定的值時,體系會出現一個、兩個或三個共振頻率,阻尼比ξ2對共振頻率的影響比ξ2的影響更明顯。