夾砂層土壤膜孔灌水分入滲規律數值模擬與試驗驗證

劉文光， 賈生海， 范嚴偉， 白貴林， 趙 彤

(1.甘肅農業大學 水利水電工程學院， 甘肅 蘭州 730070； 2.蘭州理工大學 能源與動力工程學院， 甘肅 蘭州 730050)

1 研究背景

有機融合農業耕作措施與節水灌溉技術形成綜合的節水技術體系，是節水農業關鍵技術的突破點，受到農業和土壤相關科研工作者的重視[1]。研究表明，夾砂層的存在可減小土壤水分下滲速率，提高上層土壤的水分含量[2-5]。基于夾砂土壤中水分的入滲特點，在黃土中設置砂層的耕作方法得到認可并應用[6-7]。

目前，夾砂土壤入滲機理研究主要是針對畦灌和溝灌灌水模式，取得了豐富的成果，為夾砂土壤應用提供了理論指導[8-13]。隨著地膜覆蓋技術的發展，膜孔灌逐漸發展起來，其利用地膜輸水并通過作物孔和專用孔入滲進行灌溉，具有節水、保肥、灌水均勻度高等優點，在中國西北干旱半干旱區得到應用[14-15]。以往，膜孔入滲特性研究主要是針對均質土壤，對夾砂土壤入滲特性研究相對較少。面對新形勢下農田不同節水灌溉技術，研究膜孔灌水模式下夾砂層土壤水分運動規律具有重要的現實意義，同時可為水資源高效利用提供理論依據。

隨著計算機技術的發展，采用數值模擬方法進行土壤水分運動規律的研究成為趨勢。由Simunek等[16]開發的SWMS軟件被廣泛用于模擬各種灌溉方式的土壤水分運動，并且取得了良好的效果。聶衛波等[17]采用SWMS-1D軟件對均質土一維土壤入滲特性進行了數值模擬；范嚴偉等[18]利用SWMS-2D軟件對層狀土垂直一維入滲土壤水分運動規律進行了數值模擬；Li等[19]利用SWMS-2D模型軟件對層狀土壤膜孔入滲量進行了研究，但缺少必要的驗證。

本文以室內試驗為基礎，針對土壤剖面存在砂質夾層的特點，基于Richard方程建立膜孔灌條件下夾砂層土壤水分運動數學模型，利用SWMS-2D軟件求解，通過室內試驗對模擬結果進行驗證，分析數值模擬的夾砂土膜孔灌土壤水分運動規律的合理性及可靠性。以期借助數值模擬方法，進一步認識膜孔灌條件下夾砂土壤水分運動機理，為后期模擬分析土壤特性和灌水技術要素對夾砂土體中膜孔入滲特性的影響提供技術支撐。

2 材料與方法

2.1 室內試驗

2.1.1 試驗土樣 供試壤土取自蘭州市黃峪鎮祁家營村蘋果園內；砂土取自蘭州市秦王川盆地。取土深度為5～60 cm，將土樣帶回實驗室，經風干、碾壓，過2 mm篩后制成試驗土樣，并采用激光粒度儀(MS2000)測量其顆粒級配。

參照國際制土壤分類標準，試驗土樣屬于粉壤土和砂土，土樣的基本物理特性見表1。

表1 試驗土壤基本物理特性

2.1.2 試驗方法 試驗裝置主要由馬氏瓶和有機玻璃土箱組成，如圖1所示，在土箱一角安裝有膜孔室，并在側面設置取土孔和底部設通氣孔。將制備好的土樣依照試驗方案(見表2)，以粉壤土容重為1.33 g/cm3和砂土為1.55 g/cm3分層(5 cm)裝入30 cm×30 cm×60 cm(長×寬×高)的有機玻璃土箱。試驗中，用馬氏瓶保持恒定水頭供水，按已確定的時間間隔記錄馬氏瓶讀數，并描濕潤鋒運移曲線，為防止水分蒸發在土箱上表面覆保鮮膜。試驗結束后，從取土孔取土測定試驗土體土壤含水量。

2.2 數學模型

2.2.1 基本方程 假設每層試驗土壤為理想的均質且各向同性多孔介質，不考慮蒸發、溫度以及土壤內部空氣阻力對水分入滲的影響，在每層土壤具有相同的水分運動模型表達形式且有不同特性參數值的情況下，夾砂層土壤膜孔灌為充分供水條件下的三維入滲，可通過三維土壤水分運動基本方程的定解進行數值模擬。

(1)

式中：x為橫向坐標，cm；y為縱向坐標，cm；z為垂向坐標，向上為正，cm；C(φm)為比水容重，cm-1；φm為基質勢，cm；φ為總水勢，cm；t為入滲時間，min；K(φm)為非飽和導水率，cm/min。

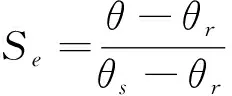
(2)

K(φm)=KsSe0.5[1-(1-Se1/m)m]2

(3)

式中：Se為土壤有效含水率，cm3/cm3；θ為土壤含水率，cm3/cm3；θr為土壤殘余含水率，cm3/cm3；θs為土壤飽和含水率，cm3/cm3；α為與進氣值成反比的經驗參數，cm-1；n和m為影響土壤水分特征曲線形狀的經驗常數，m=1-1/n;Ks為土壤飽和導水率，cm/min。

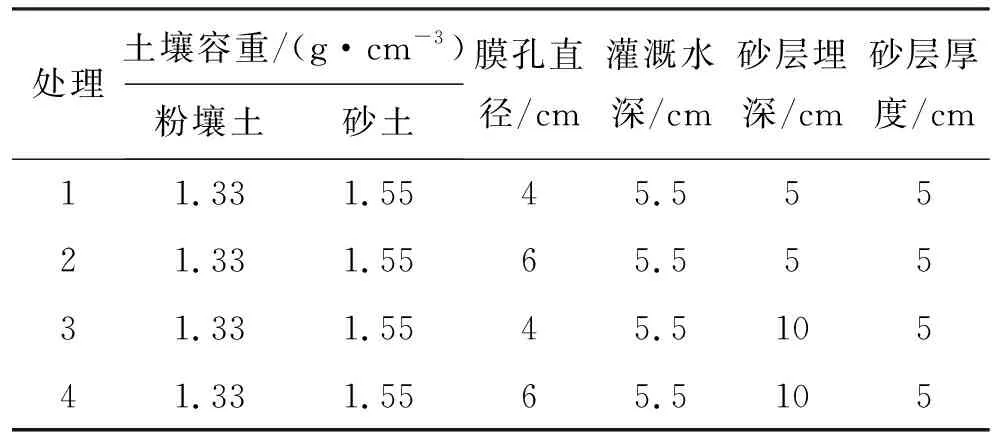
表2 夾砂層土壤膜孔灌試驗方案

2.2.2 定解條件 因膜孔具有軸對稱性，所以本試驗可以簡化為研究由1/4膜孔所控制的土壤水分入滲規律，簡化后模型如圖2所示，OBCD-O′B′C′D′表示試驗土體，其中，EFGH-E′F′G′H′表示夾砂層。由此確定的定解條件為：

(1)初始條件。

φ=φ0,t=0, 0≤x≤d, 0≤y≤d,

-h≤z≤0

(4)

式中：φ0為土壤的初始總水勢，cm；d為模擬土體的寬度，cm；h為模擬土體的深度，cm。

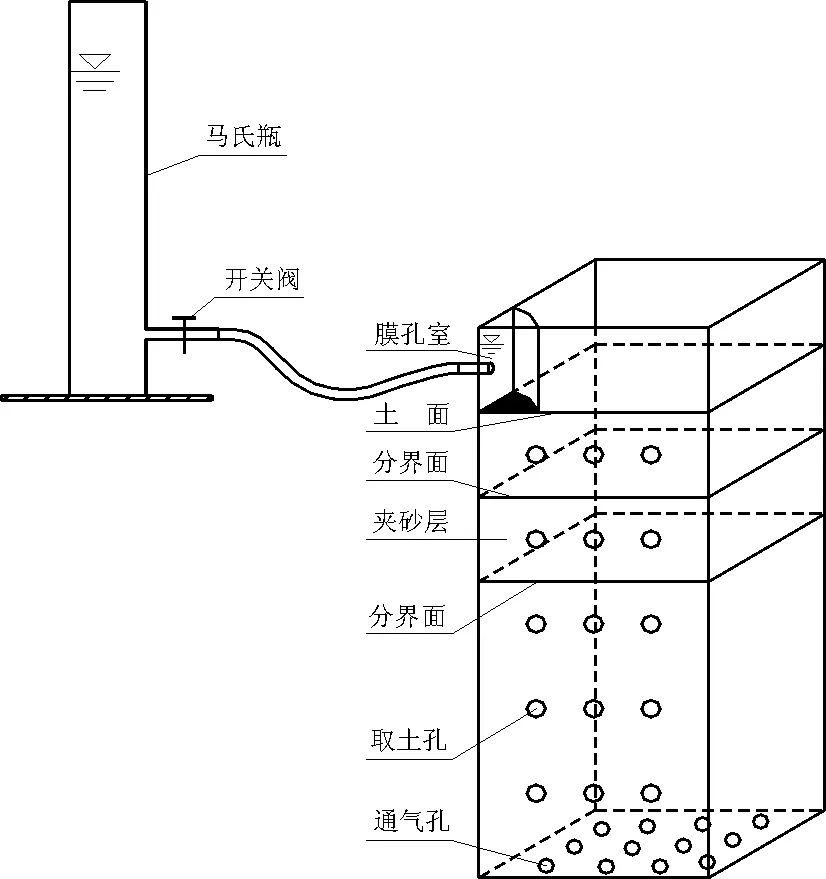
圖1 試驗裝置圖

(2)邊界條件。在試驗中，膜孔OAA′處水頭保持恒定；采用保鮮膜將上邊界AA′DCB覆蓋，因此沒有水分蒸發，所以為零通量面；由于膜孔的對稱性，1/4膜孔邊界面的OBB′O′和ODD′O′為零通量面；由于模擬土體體積較大，故可以認為邊界面DCC′D′、BCC′B′和O′B′C′D′水分不會到達，即邊界無水量交換，總水勢會保持恒定。依上述分析，邊界條件為：

邊界OAA′：

(5)

邊界AA′DCB：

(6)

邊界OBB′O′：

y=0,t≥0

(7)

邊界ODD′O′：

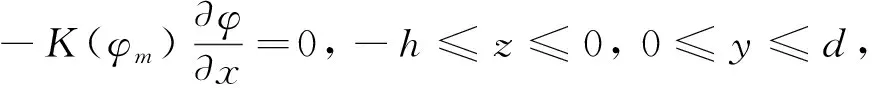
x=0,t≥0

(8)

邊界DCC′D′：

φ=φ0, -h≤z≤0, 0≤x≤d,y=d,t≥0

(9)

邊界BCC′B′：

φ=φ0, -h≤z≤0, 0≤y≤d,x=d,t≥0

(10)

邊界O′B′C′D′：

φ=φ0, 0≤x≤d, 0≤y≤d,z=-h,t≥0

(11)

式中：h0為灌溉水深，cm；r為膜孔半徑，cm；T為灌水時間，min。

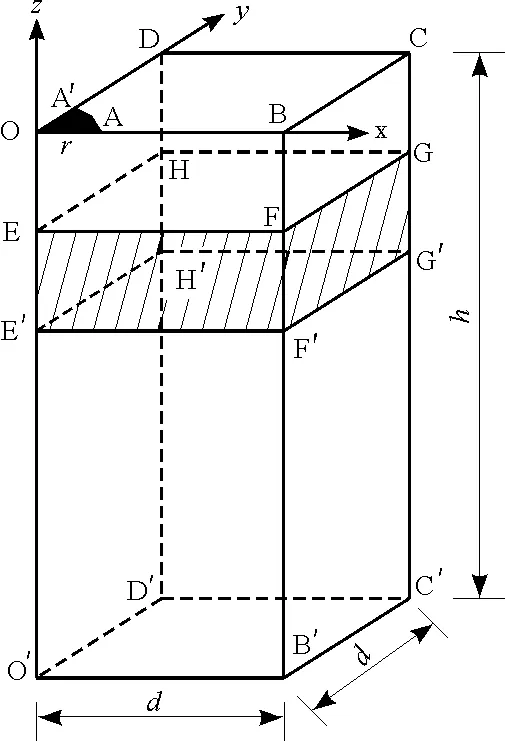
圖2 計算簡化圖

2.2.3 數值求解方法 應用軟件SWMS-2D對上述模型進行求解。將模擬土體剖面劃分為方形計算單元，z軸方向間隔1 cm，x軸方向先密后疏，計算區域的深度為30 cm，半徑為30 cm。試驗土壤的VG模型參數見表3。

2.3 誤差分析

采用以下4個指標，用于分析模擬值和實測值之間的誤差，分別為：

(12)

(13)

(14)

(15)

式中：MAE為平均絕對誤差；RMSE為均方根誤差；PBIAS為偏差百分比；NSE為納什效率系數；Yiobs為第i個實測值；Yisim第i個模擬值；Ymean為實測值的平均值；n為數據總個數。MAE、RMSE和PBIAS的數值越接近0，NSE的數值越靠近1，表示模擬值與實測值差值越小，兩者吻合越好。

表3 試驗土壤的Van Genuchten模型參數

3 結果分析

用SWMS-2D軟件求解膜孔灌條件下夾砂層土壤水分運動數學方程，獲得累積入滲量、濕潤鋒運移距離和土壤剖面含水量的模擬結果，將模擬結果與實測結果進行對比驗證。

3.1 累積入滲量的數值模擬與驗證

圖3為不同處理下夾砂層土壤膜孔灌累積入滲量的模擬值與實測值的比較。

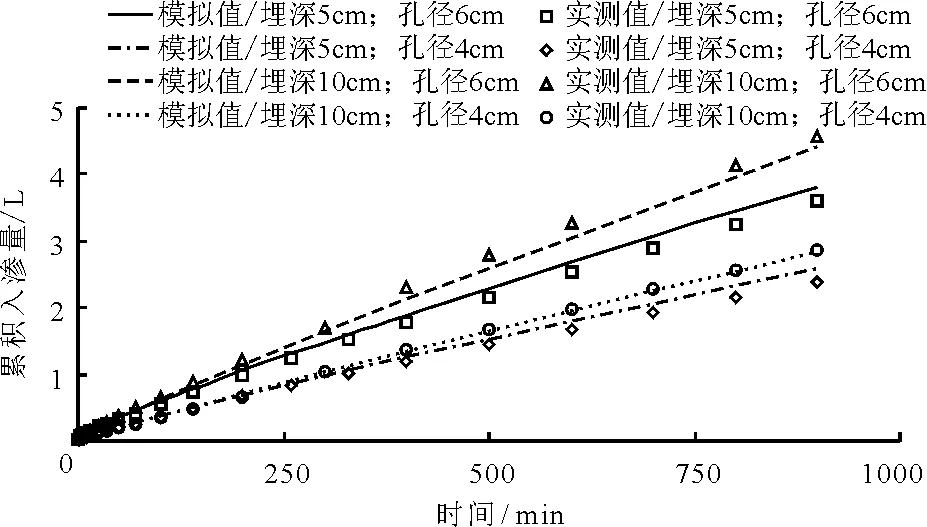
圖3 累積入滲量的模擬值與實測值對比

由圖3可以看出，膜孔直徑對累積入滲量有影響，膜孔直徑大者對應的累積入滲量較大，這是因為膜孔直徑越大，水分進入土壤的通道越大，導致其累積入滲量越大；夾砂層埋深對累積入滲量有一定的影響，夾砂層的埋深大者對應的累積入滲量較大，主要是因為入滲水分達到砂-土界面向下運動的條件是砂土的進水吸力等于界面處粉壤土的基質勢，夾砂層埋深小者的入滲水分先到達砂-土界面，隨著入滲時間的增加，夾砂層埋深小者粉壤土的基質勢增加程度較大，對應的水分入滲速率較慢，累積入滲量較小，從而表現出一定的減滲現象。

對累積入滲量的模擬值與實測值進行統計特征分析：MAE為0.05 L、RMSE為0.08 L、PBIAS為-0.81%、NSE為0.99。說明各時段數值模擬結果與實測值非常吻合，表明SWMS-2D能較好地模擬夾砂土壤膜孔灌累積入滲量的變化過程。個別處理實測值與模擬值相差較大，主要是為保持水頭恒定，在試驗開始前，需用凡士林將塑料薄膜粘貼于膜孔處，然后向膜孔室內注水至指定水位線，試驗開始時再將薄膜去除，在這一操作過程中會產生水量損失(薄膜帶出水)，從而造成開始時間段內的讀數不準確；還有裝土不均勻和讀數誤差等也會對試驗數據的準確性有一定的影響。

3.2 濕潤鋒運移距離的模擬與驗證

根據夾砂層土壤膜孔灌濕潤鋒運移的特殊性，分別進行不同處理下濕潤鋒水平向和垂直向運移距離的實測值與模擬值的對比分析，如圖4所示。

分析圖4中濕潤鋒的運動規律，可知，在其他條件相同時，膜孔直徑大者水平向濕潤鋒運移距離較大，夾砂層埋深小者水平向濕潤鋒距離較大；每一種處理下水平向濕潤鋒運移距離明顯大于垂直向，這是因為夾砂層的存在，在入滲水分到達砂-土交界面時，上層粉壤土的基質勢小于夾砂層的進水吸力，只有當兩者相等時水分才會開始下滲，于是水分會在上層土壤中蓄積并繼續向水平方向運移，而垂直向則運移緩慢。

對濕潤鋒運移距離的模擬值與實測值進行統計特征分析，模擬值與實測值的MAE為0.28 cm、RMSE為0.36 cm、PBIAS為-1.56%、NSE為0.99。說明各時段數值模擬結果與實測值一致性良好，表明SWMS-2D能較好地模擬夾砂土壤膜孔灌各個方向濕潤鋒運移的變化過程。由于在試驗中，只有當試驗土體含水量達到一定量時，才可以觀測到濕潤鋒，而且土壤中的禁錮氣體產生的壓力對入滲水流會有阻礙作用，所以，對濕潤鋒運移距離的模擬值進行適當減小。

3.3 土體剖面含水量模擬與驗證

圖5為不同處理下夾砂層土壤膜孔灌濕潤體剖面含水量的模擬值與實測值的比較，實線為surfer軟件利用模擬值繪制的土體剖面含水量等值線，圓點為實測值，原點0為膜孔中心，測點坐標為(x，0，z)，單位為cm。

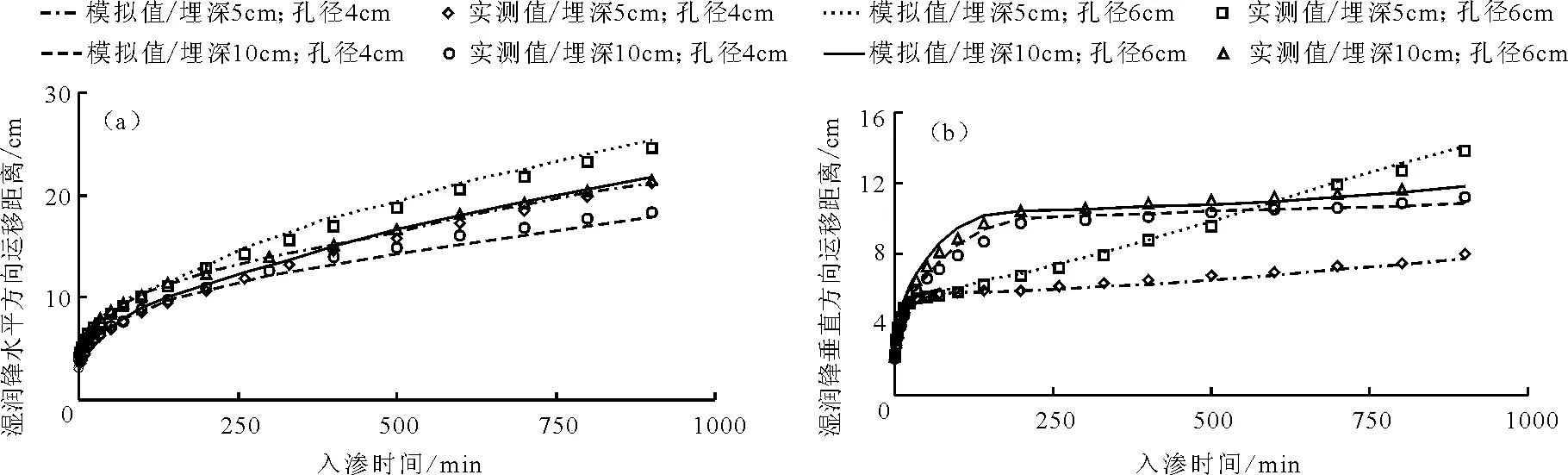
圖4 濕潤鋒運移距離的模擬值與實測值對比

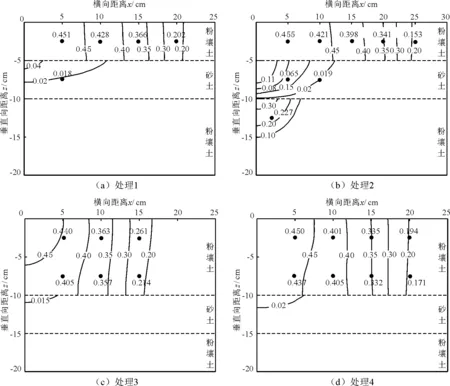
圖5 濕潤體剖面含水量的模擬值與實測值對比

分析圖5中濕潤體水分分布結果不難看出，濕潤體的濕潤鋒面形狀與均質土的半球體或半橢圓體不同，而是在粉壤土層與砂層的交界處出現了明顯的不連續性，表現出了一定的阻水性。在其他條件相同時，膜孔直徑對濕潤體水分分布有影響，膜孔直徑大者對應的濕潤體體積較大；夾砂層埋深對濕潤體水分分布有較大的影響，埋深小者入滲水分會穿過夾砂層到達下層土壤，水分會在每層土壤中重新分布，不與上層土壤的濕潤鋒面連續。

取相應點位的含水率模擬值與實測值進行統計特征分析，模擬值與實測值的MAE為0.11 cm3/cm3、RMSE為0.05 cm3/cm3、PBIAS為-6.36%、NSE為0.97。總體上，模型計算出來的濕潤體含水量的模擬值與實測值相近，表明SWMS-2D能較好地模擬獲得夾砂土壤膜孔灌濕潤體水分分布狀況。個別試驗點土壤含水量誤差較大，可能是由于土壤夯填不均勻，土鉆取土有誤差，且因取土量少造成稱量不準確等誤差產生。

4 結 論

(1)累積入滲量、濕潤鋒運移距離和濕潤體剖面含水量的模擬值與實測值的MAE分別為0.05 L、0.28 cm和0.11 cm3/cm3；RMSE分別為0.08 L、0.36 cm和0.05 cm3/cm3，PBIAS分別為-0.81%、-1.56%和-6.36%；NSE分別為0.99、0.99和0.97，說明，數值模擬結果與試驗結果具有較好的一致性。所建模型能較準確地反映夾砂層土壤膜孔灌水分運動規律。

(2)數值模擬結果與試驗結果均表明，夾砂層具有一定的阻水和減滲作用，能夠提高上層土壤的持水能力，而且使得不同處理下水平向濕潤鋒運移距離明顯大于垂直向。膜孔直徑和夾砂層埋深對累積入滲量、濕潤鋒運移距離和土體剖面含水量分布均有不同程度的影響：在其他條件相同時，膜孔直徑和夾砂層的埋深大者對應的累積入滲量較大；膜孔直徑大者和夾砂層埋深小者水平向濕潤鋒運移距離較大；膜孔直徑大者對應的濕潤體體積較大；夾砂層埋深對濕潤體水分分布有較大的影響，會使入滲水分不連續分布。

(3)本文利用SWMS-2D軟件對夾砂層土壤膜孔灌土壤水分入滲方程求解是可行的，模擬結果是可靠的。因此，SWMS-2D軟件可為進一步研究不同夾砂層質地、入滲水頭、初始含水率和夾砂層厚度等條件下的夾砂層土壤膜孔灌水分運動規律提供理論依據和技術手段。