基于混合變異策略差分進化算法的邊坡滑裂面搜索研究

張子映， 柴軍瑞， 張書濱， 錢武文

(1.西安理工大學 西北旱區生態水利工程國家重點實驗室培育基地， 陜西 西安 710048；2.江西省河道湖泊管理局， 江西 南昌 330009)

1 研究背景

邊坡滑動面搜索是邊坡穩定計算中的一個關鍵問題，其實質為安全系數[1-4]與最危險滑動面[5-7]的搜索問題。在這一領域出現了較多的優化搜索方法，模式搜索法、動態規劃法、數學歸納法、變分法、隨機搜索法等。隨著優化方法研究的深入，人工智能搜索算法如遺傳算法[8-9]、模擬退火算法、粒子群優化算法、蟻群算法[10]、神經網絡以及蒙特卡洛法[11]等被用于邊坡最危險滑動面搜索，且目前已成為滑動面搜索研究中的主流方法。這些智能尋優法各有其優點但也都存在不足之處，例如：遺傳算法存在早熟收斂、算法性能對參數選取強依賴性而參數不易確定等缺陷[9]；模擬退火算法在實際應用中由于退火不充分并不能保證一定能搜索到全局最優值；粒子群優化算法[12-13]易陷入局部最優；蟻群算法[14-15]最初被設計用于組合優化問題，其缺少用于連續數值優化的操作算子，用于邊坡滑動面搜索問題時，需要對邊坡進行一定精度的離散,操作過程復雜，同時也存在易于陷入局部最優的問題，有待進一步改進。

差分進化(differential evolution，簡稱 DE)算法是由 Storn等[16]于1995年提出的一種智能優化算法，該方法具有操作簡單、收斂性好、全局尋優能力強的優點[17-19]。錢武文等[20]受Nelder-Mead方法啟發，提出了一種名為“反射變異”的新型變異策略，具有更明確的變異方向，可即使基向量擁有一定的隨機性，但仍為一種貪婪搜索策略，為進一步增強其全局收斂性能，本文在此基礎上引入一個基本變異策略形成混合變異策略，并將該優化方法用于邊坡臨界滑動面的搜索中，通過兩個經典考核算例，驗證了該方法應用到邊坡穩定性研究是合理可行的。

2 改進的差分進化算法

算法的全局搜索能力和局部開采能力是相互對立的，變異策略高度影響著差分進化算法的性能。參考文獻[20]提出了一種名為“反射變異”的新型變異策略，并與參數自適應調整方法結合，形成了一種具有良好全局探測能力和局部開采能力的差分進化算法(RMADE)。考慮到“反射變異”從某種程度上仍屬于貪婪變異策略，仍易陷入局部最優，因此為進一步改進其全局收斂能力，本文在RMADE的基礎上引入一種基本變異策略組成混合變異策略共同控制子代個體的生成。

2.1 混合變異策略

受Nelder-Mead方法啟發，文獻[20]提出了一種名為反射變異策略的新型變異策略，該策略不論求解問題的維數，始終選擇種群中的4個任意個體組成單純形，每完成一次變異操作須引入一個單純形。該策略操作如下:

Vi,g=Xo,g+F(Xa,g-Xd,g)

(1)

式中：Vi,g為i個體在g代的試向量；Xo,g為單純形中心；Xa,g和Xd,g分別為單純形中的最好點和最壞點，F為變異縮放因子。

不同于Nelder-Mead方法，本文使用的單純形中心Xo,g是根據單純形頂點的函數值計算，并且除最壞點外的各個頂點均按其函數值權重分配到中心中。單純形中心Xo,g的計算公式如下：

(2)

式中：w1，w2和w3分別為除最壞點外的其余單純形頂點的權重；Xa,g，Xb,g和Xc,g為除最壞點外的剩余單純形頂點。

這種變異策略類似于Nelder-Mead方法中的反射操作，具有明確的搜索方向。即使基向量擁有一定的隨機性，但仍為一種貪婪搜索策略，為進一步增強其全局收斂性能，本文還引入一種基本子代生成策略(DE/current-to-rand/1)，其變異向量生成如下。

Vi,g=Xi,g+F(Xc,g-Xi,g+Xa,g-Xb,g)

(3)

式中：Xi,g為當前操作個體，其他同上。

引入DE/current-to-rand/1后，一個種群中將同時存在兩種變異策略，本文根據各策略的成功率(成功更新子代個體的比率)為各個個體輪盤賭選擇其對應的變異策略。成功率的計算公式如下：

(4)

式中：Nk為種群中使用策略k的個體總數；srk為策略k的成功率，在初始種群時將其設置為0.5，以保證算法開始時各變異策略擁有總體相等的個體數。

2.2 控制參數自適應調整機制

傳統的差分進化算法采用固定的變異因子和交叉因子，而針對不同的優化問題，使用固定的控制參數將嚴重妨礙算法的性能。

參數自適應調整機制允許每一個體使用不同于其他個體的縮放因子F和交叉因子CR去生成子代個體，且能根據算法進化過程中成功個體的經驗反饋調節控制參數。本文采用SHADE[19]算法中的參數自適應調整方法。

2.3 算法的基本思想和步驟

本文在文獻[20]中算法的基礎上，引入基本的變異策略DE/current-to-rand/1，從而進一步改進算法的全局搜索能力，并在降低早熟收斂可能性的同時保持原算法的收斂速度。使用自適應參數調節方法進一步提升了算法的整體性能。算法的具體步驟如下：

Step 1：初始化參數和初始種群；

Step 2：判定是否達到終止條件,若是轉Step 7，若否則轉Step 3；

Step 3：為每個個體分配變異因子和交叉因子；

Step 4：根據各變異策略的成功率使用輪盤賭方法為各個體分配變異策略；

Step 5：對每一靶個體，按公式(1)或(3)完成變異操作，然后完成交叉操作；

Step 6：計算試向量的函數值并與靶個體比較，選擇較優個體替換靶個體；

Step 7：輸出最優個體。

3 基于DE的邊坡穩定分析

3.1 滑動面上任意點應力張量計算

為克服極限平衡法分析結果不考慮土體應力應變狀態的缺陷，本文采用有限元軟件進行邊坡極限平衡分析，即先計算獲得邊坡高斯應力場，然后根據雙線性插值計算得到各單元節點的應力值。

(5)

式中：Ni為雙線性插值函數；ξ，η為自然坐標，本文采用笛卡爾坐標系。

生成滑動面y=y(x)，對滑動面離散成多個線單元。依次對滑動面上每個線單元的每個高斯點查找其歸屬的有限元單元，由這個單元的各個節點的方向應力形函數插值得到高斯點的方向應力，即σx，σy，τxy。

(6)

3.2 安全系數計算

(8)

式中：c、φ分別為材料的凝聚力和內摩擦角。σn、τ分別為曲線上任意一點土體方向應力和這點位置沿曲線的剪應力。

若將滑動面視為由一系列連續線段組成，將滑裂面離散化處理，應用高斯積分得邊坡安全系數為:

(9)

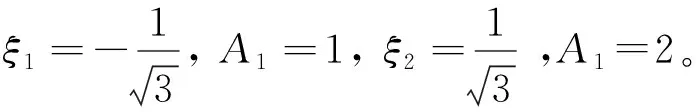
3.3 任意滑裂面構造方法

滑裂面由n個控制點{(x1,y1) , (x2,y2),…, (xn,yn) }組成的n-1個小片段近似構造。由于滑入點和滑出點都位于邊坡輪廓線上，其縱坐標y1和yn都可據已知的輪廓線求出，因此通過事先固定中間控制點的橫坐標，進一步減少搜索變量的個數，即由n個控制點近似的滑裂面的搜索變量為S={x1,y2,…,yn-1,xn}。

合理的滑裂面并非這些點在平面內任意分布的組合，通常將這些片段組成的滑裂面向上凹時視為合理，如圖1所示，這意味著滑裂面通常需要滿足以下特征[21]，即：

α1≥α2≥…≥αn-1

(10)

式中：αi為線段i的傾角；n為滑裂面控制點的個數。

式(10)亦可用線段斜率ki表示，即：

k1≥k2≥…≥kn-1

(11)

使用點坐標表示后，有：

(12)

則優化問題變為帶有n-2個約束的優化問題，優化變量為S={x1,y2,…,yn-1,xn}，即：

minF(S),S={x1,y2,…，yn-1,xn}

(13)

j=1,2,…,n-2;li≤Si≤ui；

i=1,2,…,n

在智能優化領域，約束的存在易造成可行域的減少進而使得解的搜索變得更加復雜。邊坡臨界滑裂面的搜索屬于有約束優化問題，考慮到一般情況不合理的滑裂面對應的安全系數比合理滑裂面更大的特性，可將有約束優化直接按無約束優化處理。

圖1 合理的邊坡滑動面

3.4 求解最危險滑裂面

求解最危險滑裂面的程序流程如下(程序框圖見圖2)：

(1)根據邊坡地層分布情況及邊坡剖面界限，運用有限元軟件進行合理的有限元網格劃分，并計算邊坡應力場。

(2)差分進化算法應用于滑裂面搜索，每個個體代表一個滑裂面，每個滑裂面由n個控制點組成的曲線，故每個個體就是一個n維的向量Xi=[x1,y2,…,yn-1,xn]。

(3)在算法搜索前，根據剖面的幾何模型對個體的每個維度設定合理的搜索區域。其控制方式為：第一個滑入點和最后一個滑出點的搜索范圍位于坡表，中間控制點縱坐標為搜索區間隨機初始化值y2,y3,…yn-1。

(4)構建初始種群{X1,X2,…,XNP}后，使用有限元極限平衡法計算個體Xi的安全系數Ki，用差分進化算法搜索出最佳滑裂面Xbest。

圖2 基于差分進化算法的有限元極限平衡法的流程圖

4 算例驗證

本算例使用8個滑裂面控制點(滑入點、滑出點以及6個中間控制點)，因此只需搜索滑入點和滑出點的X值以及3個中間控制點的Y坐標值。為了使中間控制點更好地反映滑面的形狀，盡可能地將中間控制點的橫坐標均勻分布在搜索域內。種群規模設置為40，最大迭代次數設為150。

4.1 均質邊坡

引用澳大利亞計算機應用協會(ACADS)通用考題1，坡高為10 m，坡角30°，土容重γ=20 kN/m3，黏聚力c=3 kPa，土的彈性模量E=104kN/m2，內摩擦角φ=19.6°，泊松比ν=0.25。推薦的安全系數為1.0。應力計算模型如圖3所示，假定區域左右邊界為法向約束，底部邊界為固定端約束。

建立有限元模型，使用理想彈塑性本構模型計算基于Mohr-Coulomb強度破壞準則的邊坡土體的應力場分布，進而以本文方法確定最危險滑動面的位置和其對應的安全系數。為了進行比較，將結果與使用傳統極限平衡法spencer、Bishop和Janbu法穩定性分析的結果比較，將各方法所得到的安全系數和最危險滑裂面匯總繪制于圖4中。由圖4可知，圓弧滑動搜索結果為KJanbu=0.966，KBishop=0.996，KSpencer=0.995，推薦安全系數為1.0。本文方法搜索的邊坡最危險滑面安全系數為1.055，僅與推薦的安全系數相差5.5%，在合理范圍，本文方法正確。

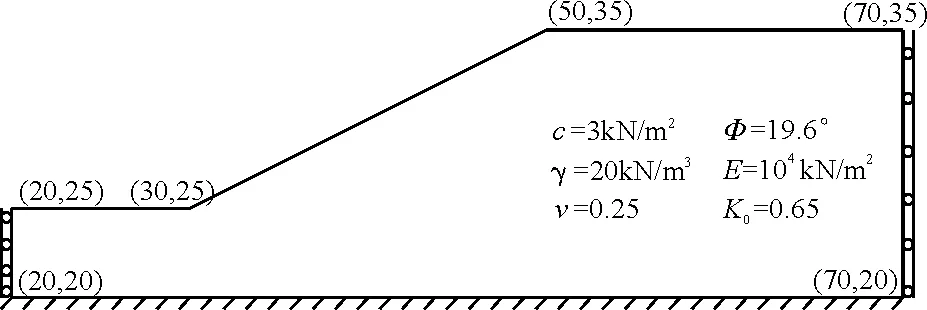
圖3 邊坡幾何模型

圖4 各方法搜索的最危險滑裂面對比

4.2 非均質邊坡

引用澳大利亞計算機應用協會(ACADS)一通用考題。坡體由3種土料構成，坡高為 10 m，坡比為1∶2，邊坡幾何特征如圖5所示，其材料特性如表1所示，推薦的安全系數為1.0。

圖5 邊坡幾何模型

表1 非均質邊坡材料性質

建立有限元模型，使用理想彈塑性本構模型計算基于Mohr-Coulomb強度破壞準則的邊坡土體的應力場分布，進而以本文方法確定最危險滑動面的位置和其對應的安全系數。同上，將各方法所得到的安全系數和最危險滑裂面匯總繪制于圖6中。

由圖6可知，圓弧滑動搜索結果為KJanbu=1.341，KBishop=1.442，KSpencer=1.419，推薦安全系數為1.39。本文方法搜索的邊坡最危險滑面安全系數為1.375，比推薦的安全系數小1.08%，在合理范圍。本文計算結果處于Janbu法與Bishop法和Spencer法之間，且略小于Bishop法和Spencer法，說明本文方法的準確性。基于有限元彈塑性變形的極限平衡法滑面起始部分較圓弧法略有“上翹”，尾部略有“下沉”，考慮到土體的彈塑性變形這種現象是可以解釋的。說明是否考慮塑性變形對邊坡的滑面位置和安全系數影響較大。

圖6 各方法搜索出的最危險滑裂面對比

4.3 收斂性能比較

使用上節非均質邊坡作為計算模型，將本文改進的差分進化算法與單純形法、DE、RMADE進行比較，研究不同算法對邊坡臨界滑動面搜索的影響。鑒于單純形法為無約束優化算法，而滑面受到邊坡坡體區域的限制，因此本文對單純形法中的初始單純形生成方法進行了略微調整，即引入差分進化算法中的初始種群技術生成初始單純形。

文中使用的單純形法的反射系數、擴張系數以及收縮系數分別為1.0、1.3和0.7，DE的縮放因子F=0.8，交叉因子CR=0.8。種群規模NP=40，最大迭代次數為200。為了研究算法搜索臨界滑面的穩定性，各算法均獨立運行10次，記錄最大值、平均值、最小值以及標準差于表2中，各算法的典型收斂過程線繪于圖7中。

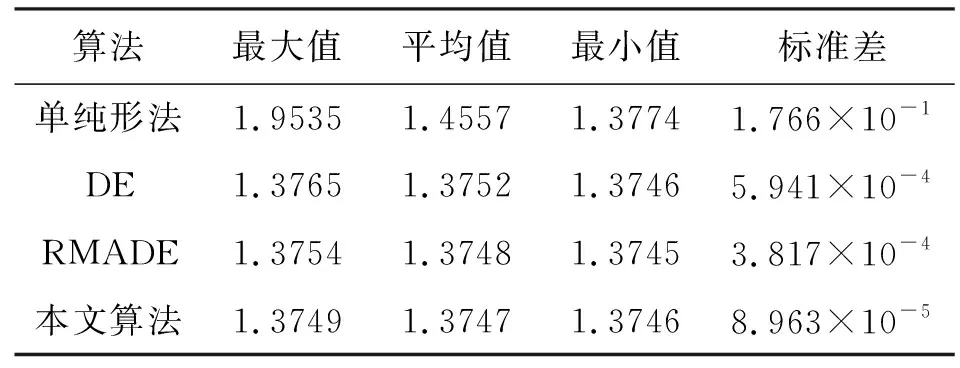
表2 獨立10次計算下各算法性能比較

圖7 各算法的收斂過程

由表2可知，單純形法結果最為發散，說明其已陷入局部最優，本文算法的平均值和標準差最小，說明其性能較其他方法要好且更穩定。由圖7可知，本文算法擁有較快的收斂速度。綜合可知，本文算法性能優于其他幾種方法，說明本文對RMADE的改進具有實際意義。

5 結 論

(1)本文在RMADE的基礎上引入一個基本的變異策略DE/current-to-rand/1而形成了一種改進的差分進化算法，該方法根據各變異策略的子代成功率使用輪盤賭選擇自動選擇個體變異策略，并與其他優化方法進行比較驗證了本文提出的算法具有更好的尋優性能。

(2)將本文改進的差分進化算法與有限元極限平衡法結合，應用于邊坡穩定性分析中，通過兩個算例驗證了該法解決邊坡穩定性問題的有效性。