基于改進logistic模型的中國社會消費品零售總額預測

趙文英 袁赫

摘 要：? 建立改進的logistic模型，預測中國社會消費品零售總額.依據中國1991-2016年社會消費品零售總額曲線變化特點和最終發展狀態，建立改進的logistic模型，利用此模型預測中國社會消費品零售總額.預測結果與其他的社會消費品零售總額模型和經典的Logistic模型預測結果相比，可信度更高，可為相關部門制定政策提供參考.

關鍵詞： 社會消費品零售總額;改進的Logistic模型;預測

[中圖分類號]F062.9 ???[文獻標志碼]A

A Predictive Parsing of Based on Improving Logistic Model'sTotal Volume of Retail Sales of Social Goods in China

ZHAO Wen-ying ， YUAN He

（Mudanjiang Normal University，Department of Mathemastics，Mudanjiang 157011，China）

Abstract： The improved logistic model has been established to forecast Chinas total retail sales of consumer goods. According to the characteristics and the trend of Chinas total retail sales of consumer goods from 1991 to 2012， the improved logistic model has been established to forecast China's total retail sales of consumer goods. The forecast results are compared with other forecast models of total retail sales of consumer goods. The model has higher credibility and can provide reference for related departments to formulate relevant policies.

Key words： total retail sales of consumer goods; improved logistic model;prediction

社會消費品零售總額能反映一定時期內人民物質文化生活水平的提高情況和社會商品消費情況，是研究人們生活水平、社會生產和貨幣流通發展趨勢以及經濟宏觀政策制定等方面的重要參考數據.合理的數學模型，可以預測社會消費品零售總額，為有關部門做出正確決策提供合理依據.社會消費品零售總額預測主要有ARIMA模型、SARIMA模型、灰色預測、相關預測以及指數平滑方法預測等.ARIMA模型和SARIMA模型屬于精度較高的基于時間序列的短期預測方法（基本按月測量數據），要求時間數列的平穩性，在預測此類經濟指標時，要對原始數據進行前期的平穩性處理，這或多或少會影響預測數據的準確度[1-5]，且不適合長期預測.灰色預測雖然適合長期預測[6]，但是灰色系統理論更適合那些具有小樣本、貧信息特點的不確定性系統的預測，對于信息豐富的社會消費品零售總額來說，其預測方法稍顯遜色.也有學者從與社會消費品零售總額的相關因素入手，建立各種回歸模型來預測其未來發展趨勢[7-9]，還有的學者利用指數平滑法建立預測模型[10]，等等.以上這些模型都沒有直接考慮這樣一個問題：隨著經濟的發展、消費結構的轉變以及人民生活條件的改變，社會消費品零售總額的增長速度在經過快速上升后會逐漸下降，并最終趨于零，即趨向于飽和狀態.本文將依據我國近26年的社會消費品零售總額數據，考慮其增長速度變化過程，在經典logistic模型的基礎上，建立改進的logistic模型，利用此模型對我國社會消費品零售總額進行預測，以期為國家制定相關政策提供參考數據.

1 社會消費品零售總額預測模型

1.1 模型的選擇

社會消費品零售總額發展趨勢最終會達到飽和狀態.社會消費品零售總額是由當前社會的經濟發展水平、人均收入、消費結構、收入分配等多種因素決定的，是一個動態的指標.改革開放以來，我國社會消費品零售總額從1991年的9 415.6億元迅速增長到2016年的332 316.3億元，是一個增長速度先慢后快的過程.當社會生產力發展到一定階段后，會受到自然環境的制約，使得經濟發展速度逐漸減緩，人民生活水平逐步趨于穩定，消費結構、收入分配等趨于合理 ，這些因素反過來會限制社會消費品零售總額的增長速度，使其增長速度也逐步減慢，并最終趨向于零，達到飽和狀態，即穩定狀態.

從我國社會消費品零售總額實際變化過程看，符合logistic曲線前半部分發展變化趨勢.根據我國1991-2016年社會消費品零售總額數據繪制圖1.由圖1可以看出，1991-2002年我國社會消費品零售總額屬于慢速增長階段，2003-2016年屬于快速增長階段.整體增長速度先慢后快，符合拉伸S型曲線的前半部分變化趨勢.我國社會消費品零售總額增長過程基本符合logistic曲線即拉伸的S型曲線的變化過程，可以在此基礎上進一步改進，以增強擬合的準確度.

1.2 改進logistic模型的建立

經典的logistic模型微分形式為：

dU dt =r（U）U=r 0（1- U K ）UU（0）=U 0 ?.? （1）

式（1）中，r 0，K為參數，U為變量，U 0為初值.假定U的相對增長率r（U）是U的線性函數，即r（U）=r 0（1- U K ）.實際上，r（U）和U的關系很少為線性函數，基本為非線性函數.根據公式（1）對我國社會消費品零售總額經濟指標作圖.可以看出，二者為非線性關系.如果這時還用U的線性函數來刻畫r（U）就會增大預測的誤差.所以，選擇r（U）與U非線性函數即高斯函數的效果遠優于r（U）與U線性函數，見表1.假設

2 結果分析與預測

由表2可知，本文所建立的logistic模型預測值整體相對誤差較低，尤其是自2009年后，預測的精確度高，其結果與羅忠德等的指數平滑模型的預測結果[10]相比，可信度更高.

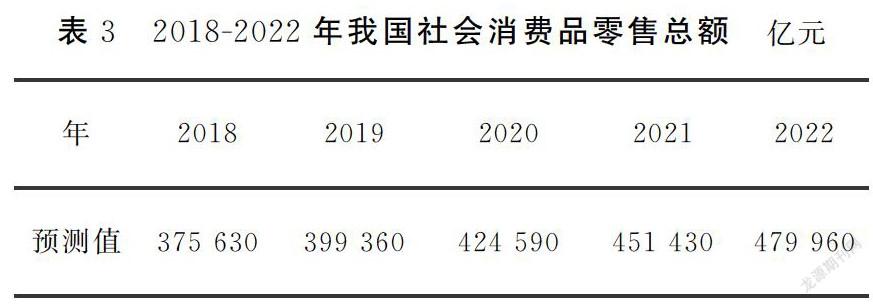
綜上所述，本文所建立的模型更適合用于 2013年以后的預測，其預測結果如表3所示，希望能為有關部門制定相關政策提供參考依據.

參考文獻

[1] ?桂梅，劉蓮花. 基于ARIMA模型對海南省社會消費品零售總額的預測[J].數學的實踐與認識， 2017，47（3）：25-30.

[2] ?萬艷蘋.基于ARIMA模型下的時間序列分析與預測-以江蘇省社會消費品零售總額為例[J].金融經濟，2008（9） ：72-74.

[3] ?李巧梅，熊國經.社會消費品零售總額ARIMA模型的建立及預測[J].科技廣場，2006（10）：4-5.

[4] ?劉領坡.我國社會消費品零售總額時間序列模型及預測[J].經濟論壇，2011（6）：5-8.

[5] ?何光優，田應福中國消費品零售總額序列的SAR I M A模型及其預測技巧[J]. 經濟研究導刊，2010，（19）：175-178.

[6] 邵民智.上海社會消費品零售總額的灰色系統分析[J].統計與決策，2005（12）：70-72.

[7] ?方湖柳.社會消費品零售總額波動規律及影響因素分析[J] 山西財經大學學報，2009，31（7）：22-28.

[8] ?石柱鮮，石圣東，黃紅梅.區域型宏觀經濟模型的開發與預測研究—兼論吉林省十五期間經濟發展前景[J].預測，2003，22（1）：53-45.

[9] ?朱宗元，王秋霞.基于傳遞函數模型的我國社會消費品零售總額預測[J].統計與決策，2010（10）：114-117.

[10] ?羅中德，賴美艷.中國社會消費品零售總額的預測分析[J].統計與決策，2013（2）：143-145.

[11] ??祖培福，張宇姣，王曉霞，張強.基于主成分分析下的黑龍江省主要國民經濟指標分析[J]. 牡丹江師范學院學報：自然科學版，2016，（1）：1-3.

[12] ?李淑鳳，謝威. 基于GM（1，1）模型的牡丹江市林產總值預測[J].牡丹江師范學院學報：自然科學版，2018（2）：24-25+38.