關于組合式箱梁橫向分布系數的探討

李保寬，周 雷，魏陸宏，楊進新

(北京市水利規劃設計研究院，北京 100048)

隨著城市建設發展和交通量日益增加，道路設計路幅越來越寬，為滿足道路寬度要求，橋梁橫向寬度亦越寬。由于道路平面線形的要求和跨越障礙物的制約，大量橋梁需采取斜交布置。寬跨比較大的橋梁和斜交角度較大的橋梁上部結構受力性能空間效應明顯，其橫向分布系數的計算能否采用常規簡化計算方法，大斜交角度對上部主梁橫向分布系數有何影響，這些都是橋梁實際設計工作中時常遇到的問題。

文章結合實際工程案例，以30m跨徑簡支組合式箱梁為對象，研究寬跨比和斜交角度對上部結構橫向分布系數的影響。組合式箱梁具有梁高低、整體性好、抗扭能力強、施工方便等諸多優點，在高速公路和城市道路20～40m跨徑橋梁工程中得到廣泛的運用。通過運用梁格法建立上部結構的有限元模型，對不同寬跨比、不同斜交角度的組合式箱梁進行上部結構受力分析，計算各種工況下主梁的橫向分布系數，歸納分析影響橫向分布系數因素及其變化規律，為實際設計工作提供參考。

1 橫向分布系數理論[1]

橫向分布系數是橋梁設計工作非常重要的參數。通過計算單梁橫向分布系數，可將橋梁結構空間模型簡化為單梁桿系模型。橫向分布系數簡化計算常用的方法主要有杠桿原理法、偏心壓力法、橫向鉸接板梁法、橫向剛接板梁法以及比擬正交板法等。在橋梁上部結構設計計算過程中，應根據施工特點、構造設計以及構件類型等不同，選擇適合的計算方法。橫向分布系數計算的主要原理：從分析荷載在橋上的橫向分布出發，求得各主梁的影響線，從而通過最不利布載計算橫向分布系數。

以上幾種簡化計算方法可以簡單、有效地計算常規橋梁上部結構橫向分布系數，但幾種計算方法均有其適用條件和局限性。杠桿原理法適用于雙主梁、橫向聯系很弱的無中間橫格梁以及橋梁支點處的橫向分布系數計算。偏心壓力法適用于寬跨比小于等于0.5，橫隔梁、橫隔板數量比較多，橫向整體性比較強的上部結構。橫向鉸接板梁法適用于各主梁間直接僅能傳遞剪力的上部結構。橫向剛接板梁法適用于各主梁間直接不僅能傳遞剪力又能傳遞彎矩的上部結構。比擬正交板法適用于由主梁、連續的橋面板和多橫隔梁所組成的較寬梁橋。以上簡化計算方法均不能考慮斜交角度對橋梁上部結構對橫向分布系數的影響。

2 梁格有限元模型

2.1 梁格法理論[2]

梁格法是借助計算機分析橋梁上部結構的一種有效的使用方法。梁格法的主要思路是將上部結構用一個等效梁格來模擬，將分散在板式或梁式每一區段的抗彎剛度和抗扭剛度集中于最鄰近的等效梁格內，實際結構的縱向剛度集中于縱向梁格構件內，而橫向剛度則集中于橫向梁格構件內。

2.2 有限元模型

以30m跨徑簡支箱梁為模型，箱梁橫斷面如圖1所示。利用Midas有限元軟件建立橋梁上部結構梁格模型，每片箱梁用梁格模型中的縱梁模擬，橋面板、端橫梁和中橫梁用橫梁模擬。分別建立橋梁橫向寬度為10片主梁(B/L=1.04)、5片主梁(B/L=0.52)和3片主梁(B/L=0.32)的梁格模型如圖2所示，并按斜交角度為0°、15°、30°和45°四種工況考慮，計算三個模型四種工況下各主梁的橫向分布系數。

橫向分布系數計算過程：分別在各片主梁跨中位置處施加集中荷載P，獲取每片主梁跨中位移f，如圖3所示，根據式(1)計算各主梁影響線，再通過橫向最不利布置荷載，最后得到每片主梁的橫向分布系數[3]。假定橋梁橫斷面均為機動車道且對稱布置，分析其中一半主梁的橫向分布系數，主梁編號從邊梁向內分別為主梁1、主梁2……。

(1)

式中，ηij—各主梁位置處的影響線坐標值；fij—在集中荷載作用在第i號主梁跨中位置在第j號主梁跨中位置處產生的撓度值。

2.3 計算結果

通過建立梁格有限元模型，得到了不同模型在斜交角度為0°、15°、30°和45°四種工況作用下各主梁橫向分布系數，并將梁格法計算結果與剛接板梁法的計算結果進行對比，匯總見表1～3。

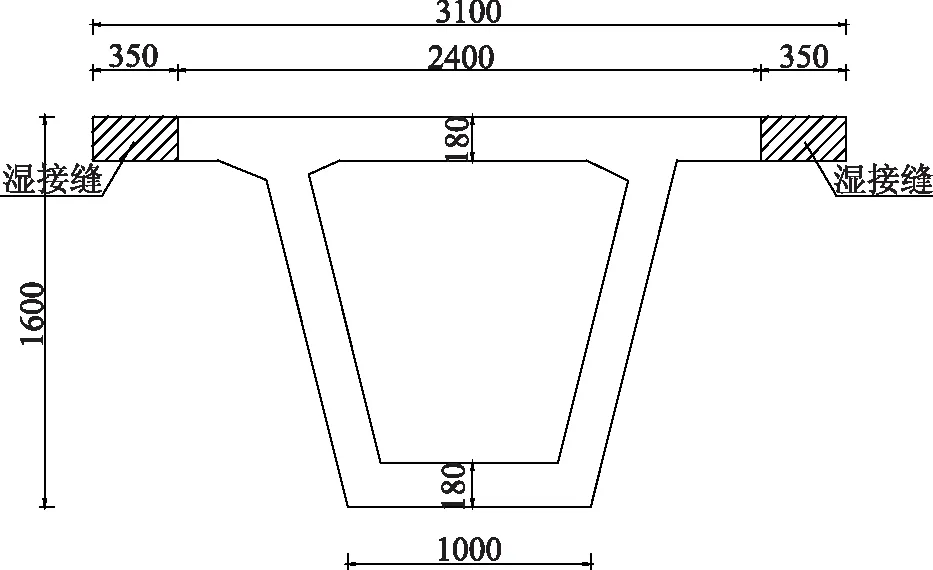
圖1 主梁橫斷面圖(單位mm)

圖2 10片主梁梁格模型(斜交角0°)

圖3 當荷載作用在主梁5時等值位移曲線(斜交角0°)

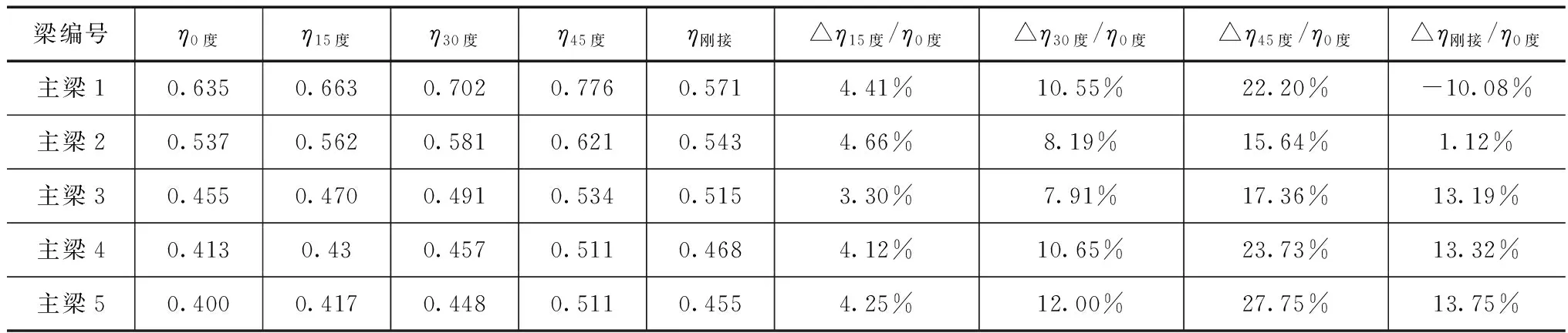
梁編號η0度η15度η30度η45度η剛接△η15度/η0度△η30度/η0度△η45度/η0度△η剛接/η0度主梁10.6350.6630.7020.7760.5714.41%10.55%22.20%-10.08%主梁20.5370.5620.5810.6210.5434.66%8.19%15.64%1.12%主梁30.4550.4700.4910.5340.5153.30%7.91%17.36%13.19%主梁40.4130.430.4570.5110.4684.12%10.65%23.73%13.32%主梁50.4000.4170.4480.5110.4554.25%12.00%27.75%13.75%

注：ηi度表示橋梁斜交角度為0°、15°、30°、45°時采用梁格法計算得到各主梁的橫向分布系數；η剛接表示采用剛接板梁法計算得到各主梁的橫向分布系數；Δηi度表示橋梁斜交角度為i度時與為0度時各主梁的橫向分布系數的差值；Δη剛接表示橋梁采用剛接板梁法計算橫向分布系數與梁格法0度時計算結果的差值。

表2 上部結構為5片主梁時(B/L=0.52)橫向分布系數

表3 上部結構為3片主梁時(B/L=0.32)橫向分布系數

通過表1～3數據，對比不同B/L、不同斜交角度對各主梁橫向分布系數的影響，結果表明，橋梁斜交角度越大，各主梁的橫向分布系數較正交時增加越明顯。同時當橋梁寬跨比較小時(B/L=0.32)，也就是所謂的窄橋，對斜交角度的敏感程度不如寬橋。不同斜交角下主梁橫向分布系數最大增長率如圖4所示。由圖4表明，當橋梁寬跨比較大時(B/L>0.5)，即所謂的寬橋，斜交角度為45°時，主梁最大橫向分布系數可增大到20%以上。

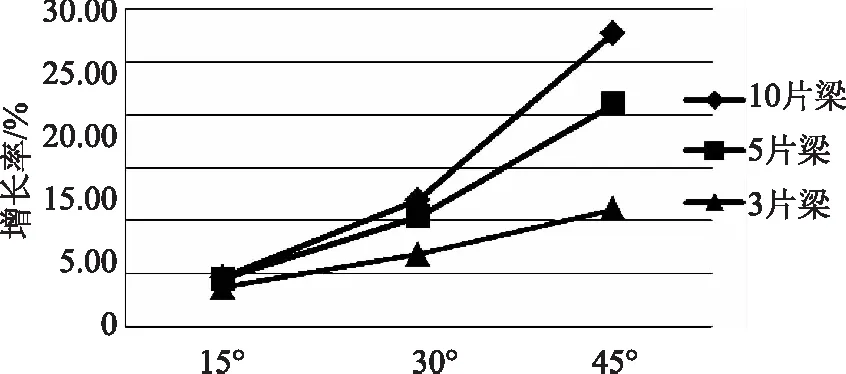
圖4 不同斜交角下主梁橫向分布系數最大增長率

通過比較梁格模型和剛接板梁法計算橫向分布系數的結果，發現當橋梁寬跨比為0.32時，主梁采用剛接板梁法計算的橫向分布系數與梁格模型結果非常接近；當橋梁寬跨比大于等0.5時，主梁采用剛接板梁法計算的橫向分布系數與梁格模型結果有一定的誤差，最大誤差可達到10%以上。

3 結論

文章采用有限元軟件建立橋梁上部結構梁格模型，分別考慮不同寬跨比和斜交角度的工況下，對組合式箱梁橫向分布系數進行計算，并對比剛接板梁的計算結果。得出以下結論：

(1)當橋梁斜交角度越大，各主梁的橫向分布系數較正交橋梁增加越明顯，同時斜交角度對寬橋影響更加明顯。當斜交角為45°時，寬橋主梁橫向分布系數較正交橋可增大20%以上，橋梁設計工作應引起重視，切勿把正交結果直接用于斜交角度大的橋梁。

(2)對于組合式箱梁橫向分布系數的計算，剛接板梁法非常適用于窄橋，而對于寬橋有一定誤差，最大誤差可達到10%以上，需根據實際情況甄選。

(3)組合式箱梁邊梁和中梁橫向分布系數均隨著橋梁寬跨比的增大而減少，當進行寬橋設計時，應使用有限元分析確定橫向分布系數，以便得到更精確的結果。

(4)由于篇幅有限，僅以30m跨徑組合箱梁為對象，研究寬跨比及斜交角度對上部結構橫向分布系數的影響，對其他跨徑的組合箱梁和結構形式橋梁有一定的參考意義。