改進煙花算法和概率神經網絡智能診斷齒輪箱故障

陳如清，李嘉春，尚 濤，張 俊

?

改進煙花算法和概率神經網絡智能診斷齒輪箱故障

陳如清1，李嘉春2，尚 濤1，張 俊3

（1. 嘉興學院機電工程學院，嘉興 314001；2. 嘉興學院數理與信息工程學院，嘉興 314001；3. 浙江大學生物系統工程與食品科學學院，杭州 310058）

針對復雜環境下農機設備的齒輪箱系統在故障診斷時存在易受現場噪聲干擾和故障識別率低等問題，提出了一種基于改進的煙花算法和概率神經網絡的齒輪箱智能故障診斷方法。為提高現有概率神經網絡模式分類方法的性能，定義了一項樣本相似度衡量指標以提高建模過程中訓練樣本的質量。將煙花算法與概率神經網絡技術有機融合提出了一種改進的煙花算法-概率神經網絡模式分類方法，利用煙花算法優化概率神經網絡的平滑參數以確定網絡參數的最優值，提高模式分類與識別精度。將改進的煙花算法-概率神經網絡模式分類方法用于噪聲環境下齒輪箱的故障診斷建模，構建故障特征參量與齒輪箱工作狀況間的復雜非線性映射關系。應用結果表明，與基于BP神經網絡、GABP（genetic algorithm back propagation）神經網絡和概率神經網絡的故障診斷模型相比，在不同程度噪聲影響下煙花算法-概率神經網絡模型均具有最高故障識別率。當噪聲控制系數為0.01、0.02、0.04和0.06時，模型的故障識別率分別為100%、95.83%、93.33%和88.33%。該研究可為非線性復雜系統的故障診斷提供了一種可行的解決方案。

齒輪；算法；噪聲；概率神經網絡；故障診斷建模

0 引 言

農業機械裝備是提高農業生產效率及推動農業可持續發展不可或缺的工具。齒輪箱既是用于轉速調節和動力傳遞的常用傳動部件，也是農機設備的重要機械部件。工作過程中其故障發生率較高，是引發機械設備故障的重要原因[1]。為確保其安全可靠運行，對齒輪與軸承等關鍵部件進行故障檢測與分類定位具有重要意義[2-3]。大型農機設備通常具有系統結構復雜、工作條件多樣且工作環境惡劣等特征，故障特征參量和設備工作狀況間形成了較為復雜的非線性映射關系[4-5]。機械設備故障機理分析和故障診斷方法研究一直受到廣泛關注，現有方法主要有模式識別方法、神經網絡方法和專家系統方法等。隨著人工智能技術的發展，基于人工智能融合技術的故障診斷方法也成為一大研究熱點[6-7]。各種智能診斷理論和方法的集成和融合，如小波分析與神經網絡集成、模糊系統與神經網絡集成和進化計算與神經網絡融合等，較好構建了故障征兆與故障類別之間的映射關系，有效實現了機械設備的故障診斷[8-10]。但對于齒輪箱等復雜非線性動態系統，現有故障診斷方法存在故障建模復雜、易受噪聲干擾和診斷精度不高等缺陷[11-12]。

從機器學習角度看，機械設備的故障診斷本質上是一個模式分類問題。概率神經網絡（probabilistic neural networks, PNN）是由Specht提出，其主要思想是將貝葉斯決策理論引入傳統神經網絡，網絡結構按照貝葉斯判別函數來設置，以實現錯誤分類的期望風險最小[13]。PNN吸收了徑向基神經網絡與經典的概率密度估計原理的優點，在模式分類與識別領域獲得廣泛應用[14-15]。與傳統BP、RBF神經網絡比較，PNN具有以下優勢：網絡學習過程簡單，學習速度快；分類更準確，對錯誤噪聲容忍性高；容錯性好，分類能力強[16]。PNN的不足之處主要體現在以下2個方面：1）對訓練樣本的代表性要求高，需要的存儲空間更大；2）網絡參數（如平滑參數）的選取直接影響PNN識別性能。此外，基本PNN通常對于每個模式類別平滑參數的取值均相同（即假設1=2=…=），不能將概率特性完整地表示出來，從而降低了PNN的識別精度。因此，如何提煉更具代表性的建模訓練樣本和選定合適的參數是PNN研究的關鍵問題。

為解決復雜環境下齒輪箱故障診斷系統易受噪聲干擾且故障識別率低等問題，本文設計了一種代表性訓練樣本提取方法，通過將PNN網絡與煙花算法（fireworks algorithm, FWA）有機結合提出了一種改進的FWA-PNN方法，利用FWA算法優化PNN的平滑參數，對于每個模式類別都不同（即→σ）。最后將本文所提出的方法用于農業機械裝備領域齒輪箱系統的故障診斷與分類定位，應用結果表明，基于改進的FWA-PNN智能診斷方法可有效提高齒輪箱故障診斷的性能。

1 PNN模式分類模型

PNN模型包括輸入層、模式層、求和層和輸出層。假設特征向量維數為3，為方便闡述，以3類模式分類器為例（即=3），PNN模型可用圖1進行描述[13,15]。圖1中，為輸入向量，11～33為訓練樣本，11～33為模式層各節點的輸出，1()～3()為求和層各節點的輸出，Output為PNN的最終輸出，表示屬于哪一類。

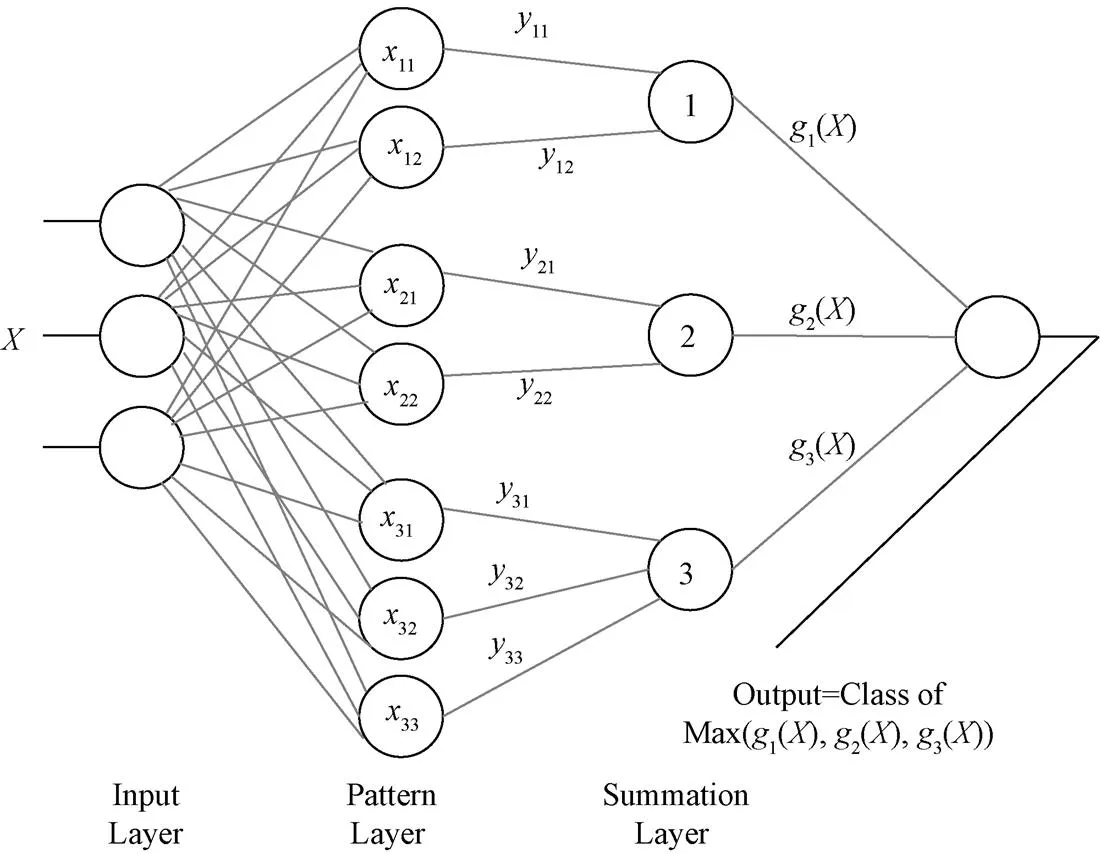
Note: ，，, (i=1,2,3; n1=2, n2=2, n3=3; σ is the smoothing parameter of PNN).

輸入層神經元個數為特征向量的維數。在輸入層中，網絡計算輸入向量與所有訓練樣本向量之間的距離。樣本層神經元個數為訓練樣本的個數，通常其激活函數為高斯函數。求和層神經元個數為類別個數，主要功能是將樣本層的輸出按類相加，相當于個加法器。競爭層的神經元個數為1。整個網絡判決的結果通過競爭層輸出，輸出結果中只有一個1，其余為0，概率值最大的那一類輸出結果為1。根據Speeht博士提出的PNN基本模型并參照現有研究文獻，基本PNN學習算法的總結如下[13-15]。

1）歸一化處理

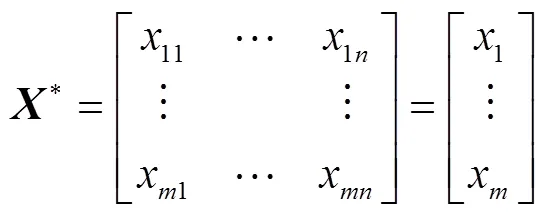
式中為訓練樣本矩陣，樣本個數為，樣本維數為，1k～x為矩陣中的一個元素。計算下面矩陣以求解歸一化因子。

2）將歸一化好的樣本送入網絡輸入層。歸一化處理后的學習樣本用表示，即

3）模式距離計算。計算待識別樣本矩陣與學習矩陣相對應元素之間的距離（歐氏距離）。

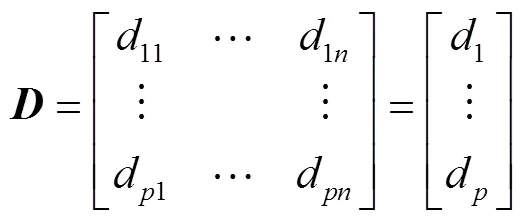
4）激活模式層高斯函數的神經元。學習樣本與待識別樣本歸一化處理后，通常取標準差=0.1的高斯型函數。激活后得到初始概率矩陣。

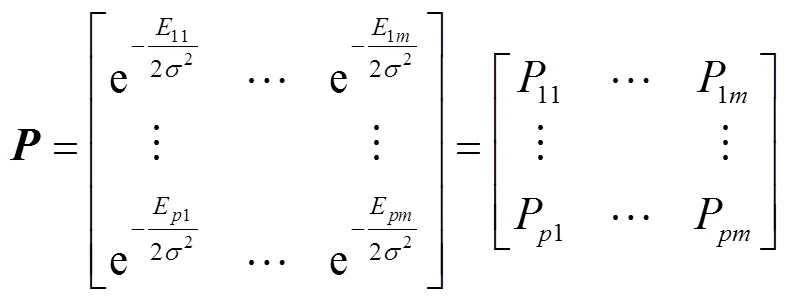
5）求和層求解各樣本屬于各類的初始概率和。

設樣本數為，可分為類，且各類樣本的數量相同。則樣本屬于各類的初始概率和為

6）計算概率，即第個待識別樣本屬于第類的概率，其中S為的第行第列元素，S為的第行第列元素。

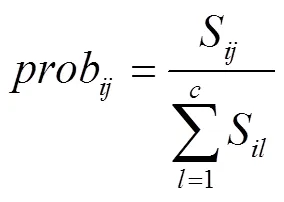
2 模式分類代表樣本的獲取

為提高PNN模式分類方法的性能，建模過程對樣本的質量要求較高。采用樣本間的相似度度量方法從原始樣本數據中篩選更具代表性的建模樣本。相似度分析時，常以樣本間的距離（如歐氏距離、馬氏距離和余弦距離等）作為度量方式。

由歐氏距離和余弦距離的定義可知，歐氏距離和余弦距離分別從不同的角度描述數據間的相似度。兩者區別主要體現在：余弦距離在描述數據間的相似度時強調兩組數據方向上的差異；歐氏距離則注重兩組數據的空間距離或位置上的差異。為更好度量數據間的相似度，發揮歐氏距離和余弦距離各自在描述數據間相似性的優勢，將余弦距離和歐式距離2種度量方法有機融合，形成一種新的樣本相似度衡量指標，即

式中dist和cos分別表示樣本間的歐氏距離和余弦距離，Abs為絕對值函數。相似度衡量指標數值越大則表示2組數據間的差異性越大，反之亦然。采用新的相似度衡量方法對PNN模式分類原始建模數據進行分析，提取更具代表性的建模樣本。獲取過程為：通過計算原始數據集中樣本兩兩之間的相似度值并設置相應的閾值，當相似度值小于設定閾值，則去除其中一個樣本。重復以上篩選過程，直至剩余樣本的數量滿足建模要求為止。提取后的樣本數據具有良好的代表性，即數據間的差異性最大或相似性最小，作為PNN的建模數據。

3 改進的FWA-PNN模式分類算法

將PNN用于解決模式分類問題時，平滑參數的選取直接影響PNN識別性能。通常平滑參數的選取并無統一規則，如何確定合適的參數是PNN建模的關鍵問題。譚營等[17-18]根據煙花爆炸產生火花這一現象提出煙花算法，其基本實現思路是將煙花視為最優化問題解空間中的一個可行解，通過煙花爆炸產生一定規模的火花，實現鄰域搜索最優解。FWA屬于有導向的隨機性啟發式算法，作為一種新型群體智能優化算法，相比傳統優化方法，其具有魯棒性較強、全局優化性能較好，局部和全局搜索能力自調節機制靈活等優勢，受到不同領域學者的廣泛關注。目前已成功用于解決神經網絡權值的訓練、連續和離散系統的參數優化及組合優化問題的求解等方面問題，取得良好的應用成效[19-21]。

針對現有PNN模式分類方法存在的分類識別精度不高和平滑參數難以確定等問題，本文將FWA優化算法與PNN神經網絡技術有機融合提出了一種改進的FWA-PNN模式分類方法。將FWA用于求解PNN平滑因子σ的優化問題，以提高PNN的模式分類與識別精度。

用于故障分類識別的改進FWA-PNN算法，運行過程具體包括以下6個步驟：

1）初始化設置。設定平滑因子σ的取值范圍，隨機產生規模為的維初始煙花種群1, …σ, …,σ∈R,1，表征平滑因子σ優化問題的個初始解，為待分類樣本模式的種類數；根據FWA算法的搜索機理初始化FWA的爆炸半徑及爆炸火花數調節常數、最大搜索次數和尋優精度等相關參數；并設當前代數=1；

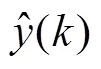
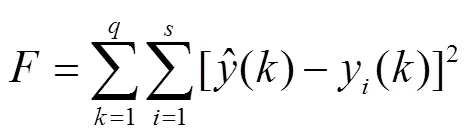
3）產生爆炸火花和高斯變異火花，從煙花、爆炸火花和高斯變異火花種群中選擇個體作為下一次迭代計算的煙花種群；

4）更新迭代次數（即增加1）；

5）檢查并根據群體最優適應度值計算誤差，判斷是否滿足終止條件。若滿足則停止搜索，否則返回步驟2）；

6）利用FWA優化算法得到的最優平滑因子σ確定PNN的網絡模型，輸入測試樣本數據，完成故障分類識別。

4 故障診斷建模與驗證

4.1 故障數據采集

齒輪箱是農機設備傳動系統中的重要部分，經常工作在強噪聲干擾、重載和特殊介質等惡劣條件下，齒輪和軸承的故障時有發生[22]。現場運行表明，較為常見的故障類型主要有齒輪崩齒、中間軸竄動、輸入軸彎曲、軸承外圈有剝落坑和軸承內圈劃傷等5類。

為獲取齒輪箱的故障建模數據，以JZQ250型齒輪箱（型號：ZQ-250；品牌：江蘇國茂；總中心距：250 mm；傳動比：40.17）為對象在實驗室模擬了6種工作狀態（含1種正常狀態和5種典型故障狀態）。利用信號采集系統的加速度傳感器獲取齒輪箱多處測試點的振動信號（采樣點數設置為2 048，采樣頻率分別設置為800、1 000和1 250 Hz，對應齒輪箱額定轉速分別為1 000、1 200和1 500 r/min。此外，為使所采集的振動信號能更加全面和真實地反映齒輪箱的工作狀態，將測試點布置在齒輪箱箱體的平面和軸承座的受力方向上[23]。

齒輪箱故障診斷系統結構如圖2所示。試驗過程中，首先利用傳感器采集正常工況下齒輪箱的振動信號。受客觀條件限制，短期內難以收集大量故障狀態下的振動信號用于故障診斷研究。通過在試驗對象中間軸的相關部位人為設置齒輪箱的上述幾種典型故障狀態（包括齒輪崩齒、中間軸竄動、輸入軸彎曲、軸承外圈有剝落坑、軸承內圈劃傷等故障情況），模擬故障工況。試驗過程中保持負載恒定，待齒輪箱轉速平穩后再次利用壓電加速度傳感器（型號：YD-81D；品牌：秦皇島協力科技）分別測試故障工況下齒輪箱的振動信號。

圖2 齒輪箱故障診斷系統結構

4.2 故障特征描述與代表樣本獲取

對不同工況下從現場采集的齒輪箱振動信號進行預處理，并對其振動特征進行時域和頻域分析，得到反應齒輪箱工況的21項時域特征參數（即最大值、最小值、均值、均方值、有效值、方差、方根幅值、絕對平均幅值、偏度、峭度、峰值、波形指標、峰值指標、脈沖指標、裕度指標、峭度指標、偏態指標、偏度系數、8階矩系數、16階矩系數和6階矩）和6項頻域特征參數（相關因子、諧波因子、譜原點矩、頻譜重心、均方譜和頻域方差）[24-25]。

為簡化故障診斷模型，根據齒輪箱體的實際工作情況，進行故障特征參數分析和故障敏感參數選取。采用KPCA方法對高維原始數據進行特征提取，分析表明前7個特征值的累積貢獻率（即攜帶的變異信息）大于85%，可以用于進行齒輪箱工作狀況識別。從特征參數集中提取對齒輪箱故障較為敏感的7個特征值，即波形指標、峭度指標、裕度指標、偏態指標、頻譜重心、頻域方差和相關因子，作為齒輪箱故障特征向量。基于PNN的故障診斷系統就是用PNN建立故障特征與故障類型間的映射關系。

通過對振動信號的時域和頻域分析，得到波形指標等7維故障特征向量。典型故障樣本如表1所示。診斷模型輸入為7維故障特征量，輸出為6維故障編碼。

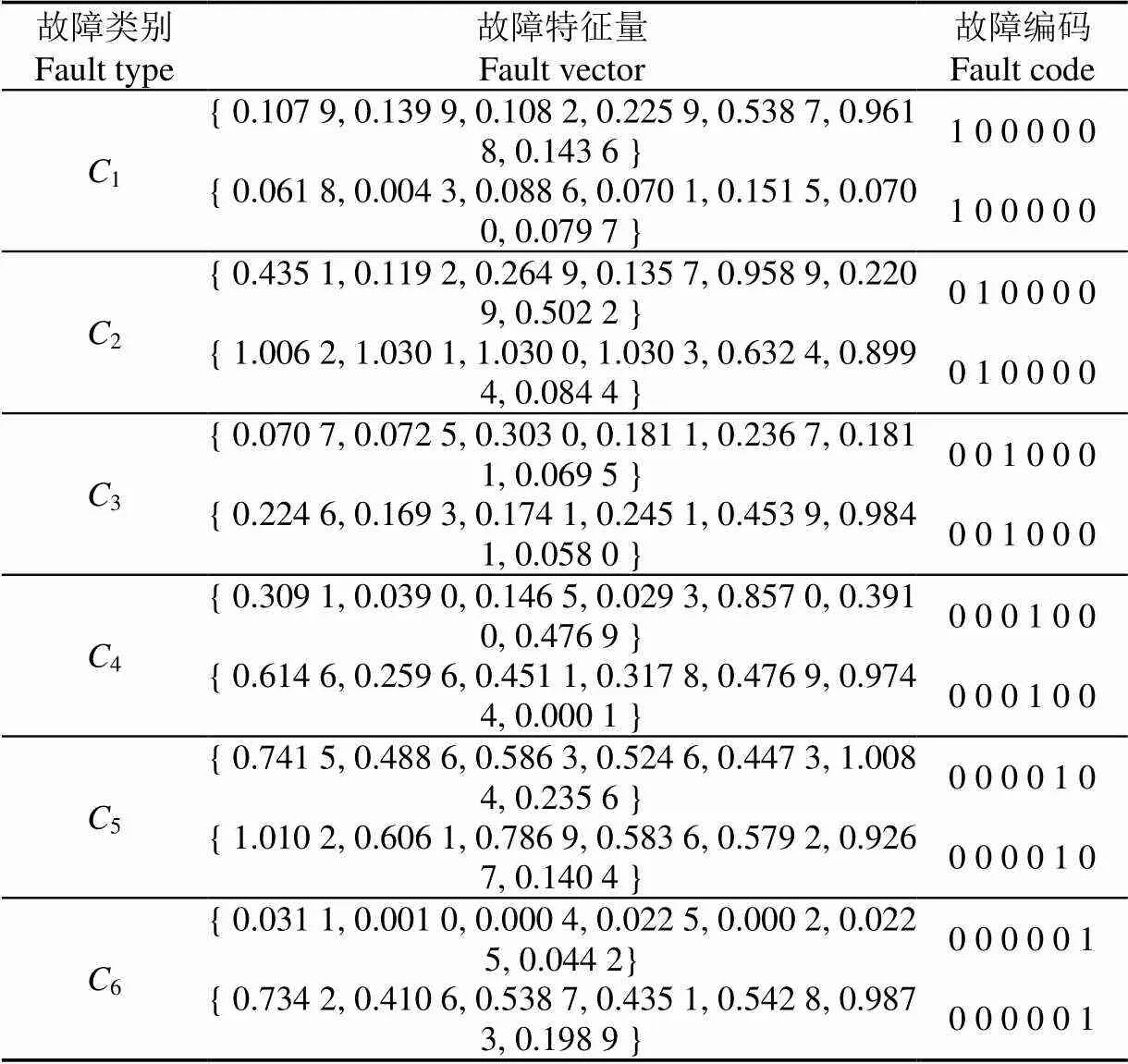
表1 齒輪箱典型故障樣本

注：1～6分別代表齒輪箱正常工況、齒輪崩齒、中間軸竄動、輸入軸彎曲、軸承外圈有剝落坑和軸承內圈劃傷等6種工作狀態。故障編碼中“1”表示故障發生，“0”表示不發生。

Note: C1～C6 represent 6 working conditions of the gearbox, there are normal operating condition, fault of gear breaking, fault of intermediate shaft playing, fault of input shaft bending, fault of spalling pits on the bearing outer ring and fault of scratching on the bearing inner race. In the fault code, the number 1 indicates fault occurring and 0 indicates normal condition.

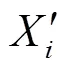
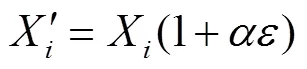
式中為人為添加的均值為0，方差為1的隨機噪聲；為噪聲控制系數，本文分別取=0.01, 0.02, 0.04, 0.06。利用式（13）在每類工作狀態下分別產生100組帶噪聲的樣本，歸一化處理后共600組樣本。針對不同程度噪聲下的故障樣本，采用前文所述“模式分類代表樣本的獲取”方法分別對6類工作狀態下的600組故障樣本進行相似度分析并剔除其中的冗余樣本。

以=0.01情況下產生的故障樣本為例，代表樣本獲取過程為：計算預處理后故障樣本集中兩樣本間的歐氏距離、余弦距離和相似度值，得到矩陣D=(δ)×l(600，1)，≥時δ取值為0。根據預處理后故障樣本的實際情況設置閾值，即當|δ|<0.18時去除當中的一個樣本。處理后故障建模樣本規模由600組精簡至339組。隨機選取其中的219組故障樣本（每類故障類別的樣本數量約36組）作為神經網絡故障診斷建模的訓練數據，其余120組作為測試數據。

4.3 基于改進FWA-PNN的故障診斷建模與驗證

將改進的FWA-PNN模式分類方法用于齒輪箱故障診斷建模，根據齒輪箱的實際運行工況，本文在進行故障診斷建模時選取的PNN拓撲結構為7-219-6-6，即輸入層神經元個數為7，對應7維故障特征量；樣本層神經元個數為219，對應219組訓練樣本的個數；求和層神經元個數為6，對應齒輪箱的6類工作狀態；競爭層神經元個數為6，與求和層相同，輸出故障診斷結果（即將求和層求解的具有最大后驗概率密度的神經元輸出為1，其余為0）。

為與FWA-PNN神經網絡故障診斷建模方法形成對比，本文還引入了BP神經網絡、GABP神經網絡（遺傳算法優化的BP神經網絡）和PNN神經網絡，分別建立不同類型的齒輪箱故障診斷模型。主要參數設置情況描述如下：

BP神經網絡：結構為7-13-6，學習算法為梯度下降法，學習率為0.01，最大迭代次數為5 000，網絡訓練目標為0.01；GABP神經網絡：初始種群規模和維數分別為20和6，交叉概率p為0.65，變異概率p為0.01，網絡結構及其他參數設置與BP神經網絡相同；PNN神經網絡：結構為7-219-6-6，平滑參數=0.1；FWA-PNN神經網絡：結構為7-219-6-6，平滑參數σ(16)通過FWA優化獲取。FWA優化算法的煙花成員規模和維數分別為20和6、爆炸半徑及爆炸火花數調節常數分別為100和80、爆炸火花數上限和下限分別為20和1、高斯變異火花數=50，參數優化過程最大迭代次數為3 000，優化精度（求和層實際輸出與理想輸出之間的偏差）為0.01。

圖3為噪聲控制系數=0.01時，基于常規BP神經網絡、GABP神經網絡和FWA-PNN神經網絡的訓練樣本誤差變化曲線。由圖3可知：基于改進的FWA-PNN故障診斷模型經過3 000次迭代后訓練精度達到0.101 6，誤差收斂速度和精度明顯優于GABP神經網絡和常規BP神經網絡。展現出良好的容錯性和較強的故障分類能力；相同條件下GABP神經網絡經3 000次迭代訓練精度為0.471 2；而常規BP神經網絡表現最差，經3 000次迭代訓練精度僅為0.865 7，經過1 200迭代后收斂速度明顯減慢，訓練精度無明顯變化，網絡陷入局部極值。

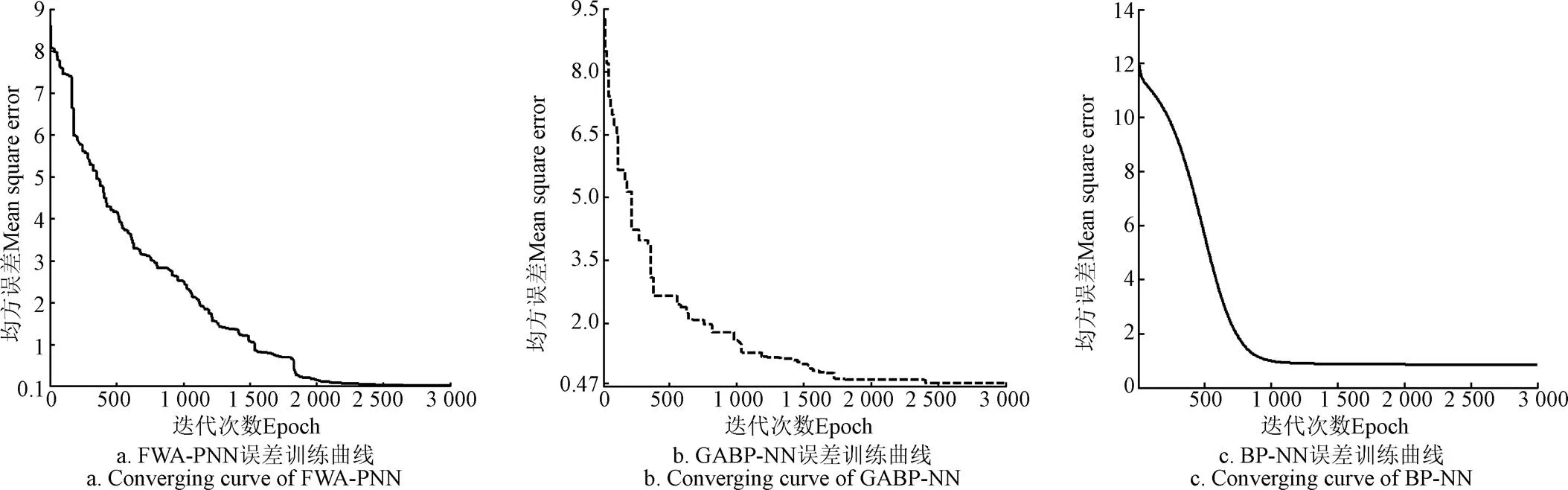
圖3 3種神經網絡訓練誤差曲線(噪聲控制系數a=0.01)

采用4種神經網絡故障診斷模型，分別對不同噪聲控制系數下的測試樣本進行故障診斷與分類定位試驗，故障識別結果對比如表2所示。故障識別率為累計正確識別個數與測試驗本總數之比值。

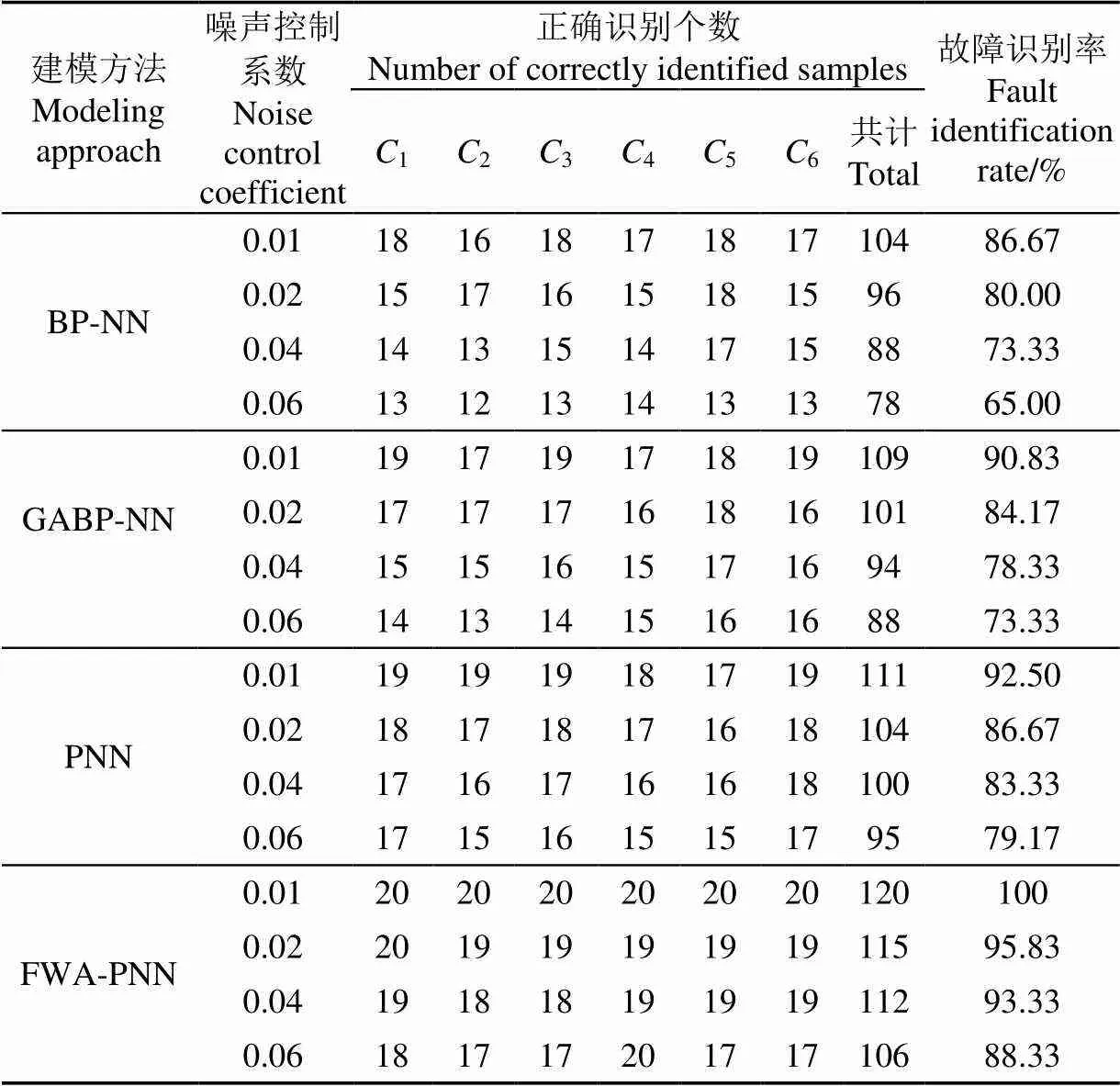
表2 3種故障診斷模型故障識別結果對比

由表2可知，故障樣本在噪聲控制系數取值較小（如0.01）的情況下，4種故障診斷模型的故障識別率均大于85%，故障識別性能較好，其中FWA-PNN模型性能最優，故障識別率達到100%；隨著噪聲程度的遞增，由于常規BP神經網絡噪聲適應能力及容錯能力較弱，模型的故障診斷精度有較大程度下降，在=0.06時，故障識別率僅為65%；GABP神經網絡模型，將全局優化性能較強的GA算法和BP神經網絡有機融合，利用GA算法對神經網絡的權閾值進行優化，有效提高了常規BP神經網絡的非線性映射能力。故障識別率有一定程度提高，但噪聲抗干擾能力不夠強；PNN神經網絡由于吸收了徑向基神經網絡與經典的概率密度估計原理的優點，具有較強的噪聲抗干擾能力，在模式分類方面較BP網絡更有優勢，整體故障識別性能優于BP網絡；FWA-PNN神經網絡由于采用FWA算法對每個模式類別的平滑參數σ進行優化，有效提高了PNN的識別精度，在不同程度的噪聲影響下FWA-PNN神經網絡模型均具有最高的故障識別率。

5 結 論

復雜噪聲環境下齒輪箱的狀態監測與故障診斷對于保障設備安全可靠運行具有重要理論意義和實用價值。為更好地實現齒輪箱的智能故障診斷，本文融合煙花算法和概率神經網絡，提出一種改進的模式分類方法并成功用于噪聲環境下齒輪箱的故障診斷建模。主要結論為：

1）為解決現有PNN模式分類方法在實際應用過程中存在對訓練樣本的代表性要求高及平滑參數難以確定等問題，一方面定義了一種樣本相似度衡量指標并設計了一種代表性訓練樣本提取方法，可有效提高PNN建模過程中訓練樣本的質量；另一方面引入一種全局優化性能較強的FWA算法用于優化PNN每個模式類別的平滑參數，以提高噪聲環境下PNN模式分類與識別的精度。

2）通過對6類典型故障情況下齒輪箱的振動信號進行分析和處理，得到相應的故障特征向量。為模擬齒輪箱的實際工況，在典型故障樣本中人為添加不同程度的噪聲并產生相應的故障診斷建模樣本。將提出的改進FWA-PNN模式分類方法用于齒輪箱故障診斷建模，建立了故障特征參量與齒輪箱工作狀況間的非線性映射關系。試驗結果表明在噪聲控制系數為0.01、0.02、0.04和0.06的情況下，該故障診斷模型的故障識別率分別為100%、95.83%、93.33%和88.33%，優于BP-NN、GABP-NN和PNN 3種故障診斷模型。本文所構建的模型能較為準確地檢測齒輪箱的各種典型故障，有效地提高了現有方法的故障診斷性能，為復雜噪聲環境下齒輪箱等非線性復雜系統的故障診斷提供一種通用可行的解決方案。

[1] 謝有浩，劉曉樂，劉后廣，等. 基于改進移頻變尺度隨機共振的齒輪故障診斷[J]. 農業工程學報，2016，32(8)：70－76.

Xie Youhao, Liu Xiaole, Liu Houguang, et al. Improved frequency-shifted and re-scaling stochastic resonance for gear fault diagnosis[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(8): 70－76. (in Chinese with English abstract)

[2] Jing L Y, Zhao M, Li P. A convolutional neural network based feature learning and fault diagnosis method for the condition monitoring of gearbox[J]. Measurement, 2017, 111: 1－10.

[3] Zhao Ming, Jia Xiaodong, Lin Jing, et al. Instantaneous speed jitter detection via encoder signal and its application for the diagnosis of planetary gearbox[J]. Mechanical System and Signal Processing, 2018, 98: 16－31.

[4] Wang L, Liu Z W, Miao Q. Time-frequency analysis based on ensemble local mean decomposition and fast kurtogram for rotating machinery fault diagnosis[J]. Mechanical System and Signal Processing, 2018, 103: 60－75.

[5] 胥永剛，孟志鵬，趙國亮，等. 基于雙樹復小波包變換能量泄漏特性分析的齒輪故障診斷[J]. 農業工程學報，2014，30(2)：72－77.

Xu Yonggang, Meng Zhipeng, Zhao Guoliang, et al. Analysis of energy leakage characteristics of dual-tree complex wavelet packet transform and its application on gear fault diagnosis[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(2): 72－77. (in Chinese with English abstract)

[6] 孟宗，胡猛，谷偉明，等. 基于LMD多尺度熵和概率神經網絡的滾動軸承故障診斷方法[J]. 中國機械工程，2016，27(4)：433－437.

Meng Zong, Hu Meng, Gu Weiming, et al. Rolling bearing fault diagnosis method based on LMD multi-scale Entropy and Probabilistic Neural Network[J]. China Mechanical Engineering, 2016, 27(4): 433－437. (in Chinese with English abstract)

[7] Jiang Guoqian, Xie Ping, Wang Xiao. Intelligent fault diagnosis of rotary machinery based on unsupervised multiscale representation learning[J]. Chinese Journal of Mechanical Engineering, 2017, 30(6): 1314－1324.

[8] Sun R B, Yang Z B, Chen X F. Gear fault diagnosis based on the structured sparsity time-frequency analysis[J]. Mechanical System and Signal Processing, 2018, 102: 346－363.

[9] Sharma Vikas, Parey Anand. Gearbox fault diagnosis using RMS based probability density function and entropy measures for fluctuating speed conditions[J]. Structural Health Monitoring-an International Journal, 2017, 16(6): 682－695.

[10] 周士帥，竇東陽，薛斌. 基于LMD和MED的滾動軸承故障特征提取方法[J]. 農業工程學報，2016，32(23)：70－76.

Zhou Shishuai, Dou Dongyang, Xue Bin. Fault feature extraction method for rolling element bearings based on LMD and MED[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(23): 70－76. (in Chinese with English abstract)

[11] 張淑清，徐劍濤，姜安琦，等. 基于極點對稱模態分解和概率神經網絡的軸承故障診斷[J]. 中國機械工程，2017，28(4)：425－431.

Zhang Shuqing, Xu Jiantao, Jiang Anqi. Fault diagnosis of bearings based on extreme-point symmetric mode decomposition and probabilistic neural network[J]. China Mechanical Engineering, 2017, 28(4): 425－431. (in Chinese with English abstract)

[12] Jia F, Lei Y G, Guo L. A neural network constructed by deep learning technique and its application to intelligent fault diagnosis of machines[J]. Neurocomputing, 2018, 272: 619－628.

[13] Chen X Y, Zhou J Z, Xiao H. Fault diagnosis based on comprehensive geometric characteristic and probability neural network[J]. Applied Mathematics and Computation, 2014, 230(3): 542－554.

[14] 鐘金童，李國龍，劉達斌，等. 基于概率神經網絡的蝸桿砂輪磨齒機徑向熱誤差建模[J]. 計算機集成制造系統，2017，23(3)：534－541.

Zhong Jintong, Li Guolong, Liu Dabin, et al. Radial thermal error modeling of CNC worm wheel gear grinding machine based on probabilistic neural network[J]. Computer Integrated Manufacturing Systems, 2017, 23(3): 534－541. (in Chinese with English abstract)

[15] 梁晴晴，韓華，崔曉鈺，等. 基于主元分析-概率神經網絡的制冷系統故障診斷[J]. 化工學報，2016，67(3)：1022－1031.

Liang Qingqing, Han Hua, Cui Xiaoyu, et al. Fault diagnosis for refrigeration system based on PCA-PNN[J]. CIESC Journal, 2016, 67(3): 1022－1031. (in Chinese with English abstract)

[16] Liu J X, Wen X B, Yuan L M. A robust approach of watermarking in contourlet domain based on probabilistic neural network[J]. Multimedia Tools and Application, 2017, 76(22): 24009－24026.

[17] 譚營，鄭少秋. 煙花算法研究進展[J]. 智能系統學報，2014，9(5)：515－528.

Tan Ying, Zheng Shaoqiu. Recent advances in fireworks algorithm [J]. CAAI Transactions on Intelligent Systems, 2014, 9(5): 515－528. (in Chinese with English abstract)

[18] Li J, Zheng S U, Tan Y. Adaptive fireworks algorithm[C]// Proceedings of 2014 IEEE Congress on Evolutionary Computation. Piscataway, NJ, USA: IEEE, 2014: 3214－3221.

[19] Zheng S Q, Li J Z, Janecek A. A cooperative framework for fireworks algorithm[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2017, 14(1): 27－41.

[20] 吳瓊，曾慶鵬. 基于多目標煙花算法的關聯規則挖掘[J].模式識別與人工智能，2017，30(4)：365－376.

Wu Qiong, Zeng Qingpeng. Association rules mining based on multi-objective fireworks optimization algorithm[J]. Pattern Recognition and Artificial Intelligence, 2017, 30(4): 365－376. (in Chinese with English abstract)

[21] Pavao L V, Costa C B B, RavagnaniM A D S. Large-scale heat exchanger networks synthesis using simulated annealing and the novel rocket fireworks optimization[J]. Aiche Journal, 2017, 63(5): 1582－1601.

[22] 李志星，石博強. 自適應奇異值分解的隨機共振提取微弱故障特征[J]. 農業工程學報，2017，33(11)：60－67.

Li Zhixing, Shi Boqiang. Extracting weak fault characteristics with adaptive singular value decomposition and stochastic resonance[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(11): 60－67. (in Chinese with English abstract)

[23] 魏秀業，潘宏俠，黃晉英. 齒輪箱傳感器優化布置研究[J]. 兵工學報，2010，31(11)：1508－1513.

Wei Xiuye, Pan Hongxia, Huang Jinying. Study on sensor optimal layout for gearbox[J]. Acta Armamentarii, 2010, 31(11): 1508－1513. (in Chinese with English abstract)

[24] He Q B, Kong F R, Yan R Q. Subspaced-based gearbox monitoring by kernel principal component analysis[J]. Mechanical System and Signal Processing, 2007, 21: 1755－1772.

[25] 李懷俊，劉越琪，謝小鵬. 齒輪箱振動與輸入能量信號的頻域相干分析與關系識別[J]. 農業工程學報，2015，31(4)：175－182.

Li Huaijun, Liu Yueqi, Xie Xiaopeng. Frequency domain coherence analysis and relationship recognition between gearbox vibration and input energy signal[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(4): 175－182. (in Chinese with English abstract)

Intelligent fault diagnosis of gearbox based on improved fireworks algorithm and probabilistic neural network

Chen Ruqing1, Li Jiachun2, Shang Tao1, Zhang Jun3

(1.,,314001,; 2.,,314001,; 3.,,310058,)

In the field of agricultural machine and equipment, gearbox was a key mechanical part that was widely applied in speed regulation and power transmission. The gearbox had a high fault rate in actual operating process due to the severe working condition and its complex configuration. State monitoring and fault diagnosing were of great significance to guarantee the safety and stability of gearbox. A fault diagnosis method based on the improved fireworks algorithm (FWA) and probabilistic neural network (PNN) was proposed to overcome the shortcomings, such as the sensitivity to environmental noise and low fault recognition rate, when conducting the fault diagnosis system of gearbox under complex operating conditions. To enhance the pattern classifying performance of traditional methods based on PNN, a new similarity measure for samples was defined, which made the quality of PNN training data increase in modeling process. An improved FWA-PNN classification method was proposed by combining FWA optimization algorithm with PNN technology. The FWA was applied to optimize the smoothing parameters of PNN to determine the optimal values of network parameters, and thus in some way the pattern classification and identification accuracy of PNN could be improved. The proposed FWA-PNN classification method was applied in fault diagnosis modeling for gearbox under noisy environment, and the complex non-linear mapping relationship between fault characteristic parameters and equipment working conditions was constructed. Experiments were carried out on JZQ250 gearbox in laboratory and the process of the fault diagnosis modeling was summarized as follows: At first, 6 working states of the gearbox that included normal state and 5 typical fault states were simulated during the experiments. And then the vibration signals of the gearbox were gained by using the accelerometers of signal acquisition system under different working conditions. After the pretreatment, time and frequency domain analysis of vibration signals were carried out and 27 time and frequency parameters reflecting the working status of the gearbox were obtained. Kernel principal component analysis (KPCA) method was applied to extract the features of the original high-dimensional data, and 7 characteristic parameters were selected as the fault feature vectors of gearbox at last. As a result, the original fault samples were generated according to the fault feature vectors. Given that the fault vibration signals of gearbox were easy to be interfered by different noises in practice, the fault modeling sample sets were regenerated by adding random noises of different levels in the original fault samples. Two thirds of the samples were randomly selected as the training data and the remaining samples were as the test data to establish fault diagnosis model for gearbox based on FWA-PNN. Next, in order to validate the effectiveness and robustness of this new model, BP (back propagation) neural network (BP-NN), genetic algorithm based BP-NN (GABP-NN) and normal PNN methods were introduced to compare with the improved pattern classification method, and 4 different fault diagnosis models were built. The training results of different neural network models indicated that FWA-PNN had better performance in error convergence speed and precision than GABP-NN and BP-NN, which had an excellent fault tolerance and fault classification capability. Finally, 4 different models were applied in fault diagnosis and classification by using the noise samples as the test data. Comparison results indicated that FWA-PNN model could effectively improve the precision of fault detection due to the smooth parameters of all pattern categories optimized by FWA. Application results showed that by compared with the fault diagnosis models based on BPNN, GABPNN and traditional PNN, the FWA-PNN model had the highest fault recognition rate under different noise levels. In conclusion, a novel fault diagnosis program for nonlinear and complex mechanical systems is provided in this paper. It has good application prospects and popularized value in fault diagnosing for agricultural machinery and equipment.

gears; algorithms; noises; probabilistic neural network; fault diagnosis modeling

2018-01-29

2018-06-30

浙江省基礎公益研究計劃項目（LGG18F030011）；國家自然科學基金資助項目（61603154）

陳如清，副教授，博士，主要從事復雜工業過程建模、機械系統狀態監測與故障診斷的有關研究。Email：10555322@qq.com

10.11975/j.issn.1002-6819.2018.17.025

TH165+.3; TH132.46

A

1002-6819(2018)-17-0192-07

陳如清，李嘉春，尚 濤，張 俊. 改進煙花算法和概率神經網絡智能診斷齒輪箱故障[J]. 農業工程學報，2018，34(17)：192－198. doi：10.11975/j.issn.1002-6819.2018.17.025 http://www.tcsae.org

Chen Ruqing, Li Jiachun, Shang Tao, Zhang Jun. Intelligent fault diagnosis of gearbox based on improved fireworks algorithm and probabilistic neural network[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(17): 192－198. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.17.025 http://www.tcsae.org