城市環境BDS/MEMS-IMU組合導航的模型誤差抑制方法

郝雨時，徐愛功，隋 心，潘 峰

(1.遼寧工程技術大學 測繪與地理科學學院，遼寧 阜新 123000；2.北京衛星導航中心，北京 10094)

0 引言

中國正在運行和正在建設的北斗衛星導航系統(BeiDou navigation satellite system，BDS)是全球衛星導航系統(global navigation satellites system，GNSS)的重要組成部分[1]，可全天候、全天時提供高精度位置信息，誤差不隨時間累積，但需保證信號實時跟蹤，且信號采樣率低、抗差性差、易受環境影響。相對于衛星導航定位系統，慣性導航系統(inertial navigation system，INS)具有短時間精度較高、可提供豐富的導航參數、采樣率高、自主性強的優勢，其劣勢是誤差隨時間累積較快，無法長時間提供高精度導航參數。BDS/INS組合導航系統結合2種技術的特點，實現優勢互補，BDS抑制INS誤差累積，INS輔助BDS信號跟蹤，保證長時間高精度、高頻率、較豐富的導航參數解算。隨著微機電系統(micro-electro-mechanical system，MEMS)及慣性測量單元(inertial measurement unit，IMU)技術的發展，MEMS-IMU以體積小、成本低的優勢，在大部分組合導航應用中逐漸取代了高成本的光纖或激光慣導[2]，基于BDS/MEMS-IMU組合導航理論研究具有深遠意義。

擴展卡爾曼濾波(extended Kalman filter，EKF)常用于組合導航數據處理，其精度依賴于系統、觀測模型精度，以及精確噪聲統計信息[3]。對于城市環境BDS/MEMS-IMU組合導航應用，常出現衛星數目少甚至無可視衛星的情況，單衛星導航定位系統無法保證連續高精度定位，同時MEMS-IMU誤差累積迅速，導致模型精度難以維持，噪聲統計信息不易獲取，采用傳統EKF難以實現參數最優解算。有關控制異常誤差影響的方法有抗差卡爾曼濾波[4]、自適應卡爾曼濾波和抗差自適應卡爾曼濾波[5-8]等。文獻[4，7-9]提出將自適應抗差濾波理論從不同角度對卡爾曼濾波進行改進，在組合導航應用中取得了明顯效果。

本文在系統噪聲參數優化方面，通過比較當前預測殘差協方差與理論誤差協方差，調諧系統噪聲協方差一步預測；在觀測噪聲參數優化方面，本文根據BDS觀測值觀測情況，評估觀測噪聲影響，對觀測噪聲參數進行進一步調諧，提升組合導航模型狀態參數解算精度。

理論上，BDS/MEMS-IMU緊組合具有可行性，緊組合可充分利用BDS觀測值信息，不受可視衛星數量約束，誤差補償能力高于松組合；但在城市環境應用中，BDS信號無法保證連續跟蹤，衛星信號頻繁失鎖且受多路徑效應影響，觀測值存在較大的觀測噪聲，較大的觀測噪聲會通過系統模型對狀態估計產生正反饋而導致濾波發散，狀態參數遠離真值[9]。從濾波器設計的應用角度來說，選取一個理論上次優的濾波器比理論上最優但易受模型誤差影響而崩潰的濾波器更為重要。因此，本文討論的BDS/MEMS-IMU組合導航模型采用松組合的形式，即觀測量為來自2個系統解算的位置及速度的差值，其中BDS定位方式采用基于相位的動態相對定位。

1 BDS/MEMS-IMU組合導航模型

本節介紹的BDS/MEMS-IMU組合導航模型包括系統模型及觀測模型。推導過程在文獻[10-12]中均有詳細介紹，不作為本文的研究重點。

1.1 系統模型

本文討論的BDS/MEMS-IMU系統模型采用姿態漂移角誤差模型，由INS位置rc、速度vc及漂移誤差角ψ的導航方程擾動分析獲得[13-14]，表達式為

(1)

(2)

1.2 觀測模型

1.2.1 位置誤差觀測方程

IMU與BDS接收機物理位置關系如圖1所示。

圖1 IMU與BDS接收機位置關系

圖1中lb為載體坐標系下杠桿臂。p系下由IMU推算的BDS接收機位置天線相位中心位置表達式為

(3)

假定lb無標定誤差，對式(3)做擾動分析得

(4)

(5)

式中εr為BDS位置觀測噪聲。BDS/MEMS-IMU位置誤差觀測方程為

(6)

1.2.2 速度誤差觀測方程

對式(4)求導[15]得

(7)

假定杠桿臂無標定誤差，對式(7)做擾動分析得

(8)

(9)

式中εv為BDS速度誤差，以BDS序貫解算過程中北東地速度標準差取代。BDS/MEMS-IMU速度誤差觀測方程為

(10)

2 噪聲參數優化

卡爾曼濾波是一種線性最小方差估計方法[13]，廣泛應用于多源數據融合解算。對于城市環境BDS/MEMS-IMU組合導航應用過程，模型結構、狀態參數及噪聲統計信息存在未知部分，且存在較大的系統及觀測噪聲。為實現參數最優解算，需優化相關噪聲參數(如系統噪聲協方差矩陣Qk、觀測噪聲協方差矩陣Rk及初始誤差協方差矩陣P0)，以實現狀態參數最優化解算。

P0反映濾波初始狀態誤差水平，影響濾波解算初期收斂速度，對全局影響較小，無需作為參數優化的重點。Qk反映狀態參數的噪聲強度[14]，Rk反映觀測值噪聲強度，二者大小影響卡爾曼增益的計算，即決定狀態參數解算對系統模型及觀測模型的依賴程度[15]。因此優化Qk、Rk為濾波器噪聲參數優化的重點。

2.1 系統噪聲參數優化

系統噪聲協方差矩陣Qk無法直接控制，可利用自適應因子α調諧Pk一步預測。協方差一步預測表達式為

(11)

(12)

(13)

式中α的隸屬函數表達式為

(14)

式中：c0為常數，可取1～1.5。若α小于1，系統預計正常，系統噪聲協方差預計接近真實的噪聲特性；反之，系統預計異常，可根據式(11)將Pk，k-1適當放大，則卡爾曼增益增大，抑制了狀態參數解算受系統模型誤差影響的程度。

2.2 觀測噪聲參數優化

預測殘差可反映系統模型精度及穩定性，其前提是觀測值精度可靠，或觀測噪聲特性較精確已知；但實際應用中，觀測值無法長期保證穩定的精度，即Rk不能符合真實的噪聲特性。若式(14)探測到系統異常，經過式(11)計算，導致濾波解算依賴觀測值精度，易擴大觀測噪聲的影響。較大觀測噪聲對狀態估計產生正反饋可導致參數估計發散不可逆[17]。

對于理想卡爾曼濾波器，給出一致的估計誤差與不確定度也能得到狀態參數穩定估計[18]，考慮帶寬限制下的觀測噪聲時間相關性及同步誤差，適當放大Rk是有必要的，一般要給出相應標準差2到3倍的狀態不確定度。令

(15)

式中：εr、εv分別為BDS解算的位置及速度的觀測噪聲，即BDS序貫解算過程中的誤差協方差，反映BDS解算過程的濾波精度，其大小往往小于真實絕對誤差；ρ為抗差因子。美國國家海洋電子協會(National Marine Electronics Association，NMEA)認為，位置精度衰減因子(position dilution of precision，PDOP)、模糊度固定成功率P、可視衛星數N、εr、εv皆可直接或間接反映車載衛星定位解算質量。本文根據NMEA協議，構建ρ的隸屬函數，量化以上指標對觀測噪聲的影響，隸屬函數構建流程如圖2所示。

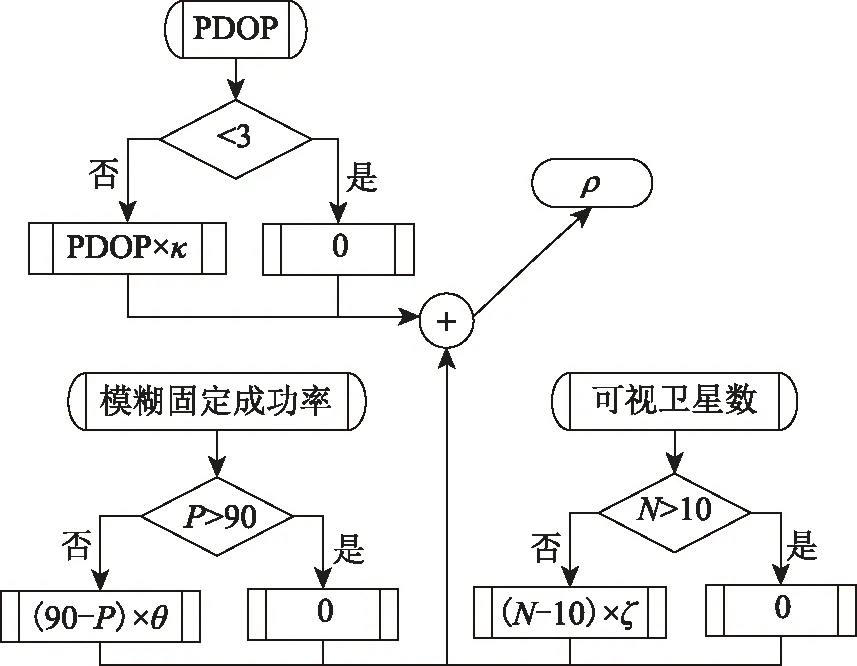
圖2 觀測噪聲參數優化

ρ的作用在于根據觀測值質量調諧觀測噪聲協方差。κ、η、ζ及θ為量化參數，用以量化觀測數據質量，可取0.1～0.5，以保證Rk在適當的范圍內放大。

需要說明的是，為避免較大觀測噪聲通過系統造成估計偏差，需在執行式(13)之前先進行觀測噪聲協方差優化。

3 實驗與結果分析

3.1 實驗方案與環境

為測試噪聲參數優化機制對BDS/MEMS-IMU組合導航的改善程度，本文設計2種實驗方案，比較其主要導航參數(平面位置、姿態角)的濾波精度及與參考結果的相對偏差。

方案1)利用標準EKF處理BDS/MEMS-IMU組合導航數據；

方案2)利用加入噪聲參數優化機制的EKF處理BDS/MEMS-IMU組合導航數據。

參考結果由光纖級別的定位定姿系統(position and orientation system，POS)提供，其GNSS系統采用GPS/BDS/GLONASS三系統，IMU級別為光纖級。參考POS系統及本文測試的POS系統(BDS/MEMS-IMU)精度指標如表1所示。

表1 精度指標

圖3表示 BDS觀測值情況及定位觀測值結果質量。

圖3 BDS定位質量

圖3中，參考POS系統的IMU及BDS/MEMS-IMU系統的IMU采樣率皆為200 Hz，GNSS采樣率為1 Hz，采樣時間為1 527 s，空間里程8 715.094 m。根據BDS觀測情況，可以看出城市環境下，BDS系統解算頻繁出現異常，如PDOP值過大、模糊度固定成功率低等。

3.2 結果與分析

2種方案的濾波收斂結果如圖4所示。

圖4 2種方案濾波精度

由圖2～3可知，相對于標準EKF，加入噪聲參數優化機制可以提升組合導航模型的濾波精度，平面位置及漂移誤差角的穩態值有降低趨勢。對于平面位置濾波精度，2種方案的平面位置濾波收斂結果均有6個尖刺點，通過對比其大小，可以認為方案2提升了惡劣環境下平面位置的濾波精度，提高約2/3。對于漂移誤差角濾波精度，方案1的平面漂移誤差角約為0.1°，垂向漂移誤差角約為0.5°；方案2的平面漂移誤差角為0.01°，垂向漂移誤差角約為0.047°。通過對比2種方案的濾波收斂情況，可以認為加入采樣噪聲參數優化機制能夠提升惡劣環境下組合導航模型平面位置的濾波穩定性，且明顯提升本文討論的導航模型的姿態濾波穩定性。

2種方案的相對偏差如圖5所示。由圖5可知：對于平面位置，結合噪聲參數優化機制后，誤差峰值有所降低，出現尖刺點比率明顯降低；對于姿態誤差，橫滾角及俯仰角精度均有提升，航向精度提升明顯。可以認為噪聲參數優化機制的介入對參數解算穩定性及精度提升均有意義。

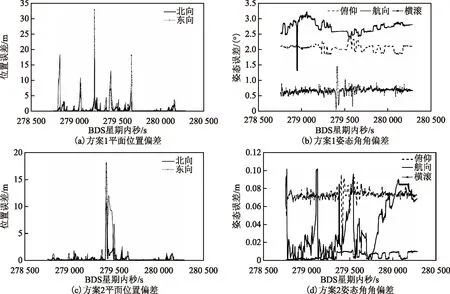
圖5 2種方案結果偏差

4 結束語

本文討論了一種噪聲參數優化方法，包括基于分析預測殘差的系統噪聲參數優化及基于BDS觀測情況的觀測噪聲參數優化方法，應用于城市環境下車載BDS/MEMS-IMU組合導航模型。實驗結果證明，對于城市環境車載BDS/MEMS-IMU組合導航應用，加入噪聲參數優化機制可提升模型的穩定性，提升位置、姿態參數的精度。