RBF神經網絡輔助的UWB/INS組合導航算法

徐愛功，蔡贛飛，潘 峰，隋 心，郝雨時，劉 韜

(1.遼寧工程技術大學 測繪與地理科學學院，遼寧 阜新 123000；2.北京衛星導航中心，北京 100094)

0 引言

隨著人們在室內環境下的工作與活動時間日益增多，人們對室內定位的需求也隨之增大[1]。常用的室內定位技術有藍牙定位、超寬帶(ultra wide band，UWB)定位、超聲波定位等。其中，超寬帶定位是一種利用非正弦波脈沖來傳輸信息的無線通信技術，憑借其功率消耗低、穿透能力強等特點，UWB及相關技術廣泛應用于室內定位研究[2]。但UWB測距信號抗差性較差，對定位精度影響很大[3]。慣性導航系統(inertial navigation system，INS)是一種不依賴外界環境的自主式導航系統，具有短時間定位精度高、抗干擾能力強等優點[4]。但INS誤差會隨時間迅速累積而導致定位結果發散。UWB/INS組合既能利用UWB抑制INS誤差隨時間的累積，又能利用INS彌補UWB輸出頻率低、信息單一的缺陷，提供高頻率、豐富的導航參數信息[5-6]。但在UWB/INS組合導航中，由于室內環境復雜，UWB信號很難保證持續跟蹤，當能接收到信號的基站個數較少時，UWB/INS組合導航系統中只有INS系統單獨定位，定位結果會很快發散。針對這種情況，一般可以通過采用更高精度的INS傳感器或加入其他傳感器到組合系統中的方式進行解決，但會增加組合系統的復雜性與成本。因此需要確定一種合適的方法，該方法既可以保證組合系統定位精度的連續性也不需要額外增加硬件的成本。

在UWB/INS組合定位過程中，當UWB信號未中斷時，UWB/INS組合定位方法可獲得高精度的定位結果，而此時單獨INS系統的定位精度會隨著時間累積而變差，在此期間，如果能夠采用一定的方法確定出單獨INS系統的定位結果與UWB/INS組合定位結果之間的映射關系，那么在UWB信號中斷后，可以利用UWB信號未中斷時所確定出來的映射關系來對單獨INS系統的定位結果與UWB/INS組合定位結果之間的差值進行預測，進而對單獨INS系統進行位置誤差補償，用INS單系統補償后的定位結果作為組合系統的定位結果以實現UWB/INS組合系統定位精度的連續性。徑向基(radial basis function，RBF)神經網絡由較小的單位神經元組成，使用與人腦結構和功能類似的學習算法，它將輸入值映射到輸出值，可以用來解決建模非常復雜和非線性的隨機問題[7-9]。

根據以上分析，可以認為RBF神經網絡的理論特性適合于UWB/INS組合定位系統的數據解算過程，可以采用RBF神經網絡對UWB/INS組合導航算法進行輔助；因此本文將對基于RBF神經網絡輔助的UWB/INS組合導航算法進行研究。

1 UWB/INS組合常規濾波算法

1.1 RTT定位測速

UWB常用的測距方法有信號往返傳播時間法(round-trip time，RTT)、到達時間/時間差法(time/time difference of arrival，TOA/TDOA)、信號到達角度法(angle of arrival，AOA)等[10]。其中，RTT測距是通過測量UWB脈沖在基準站和流動站間的往返時間間接完成距離的，這種方法不需要基準站和流動站間的時間同步[11]；因此本文選擇利用RTT測距方法解算的結果與INS解算的結果進行組合濾波。RTT測距原理如圖1所示。

圖1 RTT測距原理

圖1中：tm為流動站發送信號的時刻；ts為流動站接收信號的時刻，則流動站與基準站的距離表達式為

(1)

式中：c為光速；di和ti分別是第i個基準站到流動站的距離和標準時間偏差改正；N為基準站的個數。

設N個固定基站的平面坐標為(xi，yi)(i=1，2，…，N)，流動站平面坐標為(x，y)，由此可以推導出

(2)

V=AX

(3)

式(3)的最小二乘算法的解[12]為

(4)

式中:P為單位權陣。則UWB流動站速度信息為

(5)

式中：vx，k、vy，k為k時刻UWB的速度；xk+1，yk+1為k+1時刻UWB的位置；xk-1、yk-1為k-1時刻UWB的位置；T為UWB的采樣間隔。

1.2 UWB/INS組合導航模型

在UWB/INS組合中，數據融合方法大多基于卡爾曼濾波器。設ΔT為INS的采樣間隔，δxk、δyk、δvx，k、δvy，k表示INS在k時刻的位置和速度誤差，本文以INS的位置和速度的誤差作為狀態向量，通過卡爾曼濾波對狀態向量進行估計，對組合導航系統進行位置和速度的修正。系統的狀態向量可以表示為

Xk+1=FXk+wk

(6)

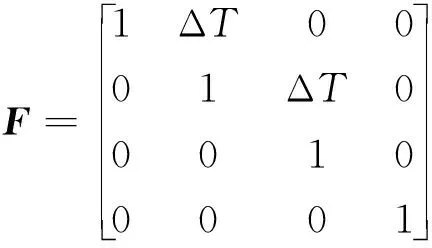
Zk=HXk+ωk

(7)

通過卡爾曼濾波即可對載體的導航信息進行更新[13]，即

(8)

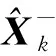
2 RBF神經網絡輔助的UWB/INS組合導航算法

2.1 RBF神經網絡原理

RBF神經網絡是一種具有3層結構的前向神經網絡[14]。輸入層由一些感知節點組成；隱藏層由僅有一層的節點組成，輸入空間經過非線性變化到隱藏空間；輸出層由隱藏層經過線性轉換得到。相對于其他的神經網絡，RBF神經網絡的局部調諧神經元能讓自身的學習收斂速度更快，緊湊的拓撲結構讓自身結構更加簡單，單層的隱藏層讓自身的表達更容易，這些優點可以讓RBF神經網絡更好地逼近任意的非線性函數[15]；為此，本文用RBF神經網絡來輔助UWB/INS組合導航。RBF網絡最常用的結構如圖2所示。

圖2 徑向基神經網絡結構

圖2中：(x1，x2…xp)∈R為網絡的輸入矢量；p為輸入矢量的個數；φi(x)為徑向基函數；Wi∈Rn為輸出權矩陣；i=1，2,…,N，N為隱含層神經元個數；Y∈Rn為網絡的輸出矩陣。本文選取高斯核函數為徑向基函數，有

(9)

式中：x為輸入矢量；ci、σi為第i個隱含層神經元的中心和寬度。用最小二乘算法求隱含層和輸出層間的權Wi，計算公式為

(10)

式中：h為數據中心的個數；q=1，2，…，p；‖·‖為歐式空間的距離范數；cmax為所選取中心的最大距離。

神經元的寬度計算公式為

(11)

2.2 RBF神經網絡輔助的UWB/INS組合導航

圖3 RBF神經網絡輔助UWB/INS組合導航結構

3 實驗與結果分析

為了驗證RBF神經網絡輔助的UWB/INS組合導航算法的有效性，在某地下停車場進行了一次模擬實驗。其中INS儀器為SBG公司的Ellipse-N-G4A2-B2，輸出頻率為200 Hz，加速度計隨機游走為14.7×10-4m/(s2·Hz0.5)，加速度計零偏為4.9×10-2m/s2，陀螺零偏為0.2 (°)·(s-1)，陀螺角度隨機游走為0.18 (°)·(h-1·HZ-0.5)。UWB儀器為Time Domain公司的PulsON400，輸出頻率為10 Hz，在信號通視條件下測距精度優于10 cm。實驗中UWB的3個基準站以接近正三角形的方式進行布設，UWB流動站和基準站在實驗過程中無任何遮擋，INS和UWB流動站固定在小車上，小車沿著設定好的軌道運行，小車初始和終止速度設置零，初始的位置為UWB流動站開始運行的坐標值，整個實驗過程運行360 s。

為了評價所提算法的性能，本文從絕對誤差(absolute error，AE)、均方根誤差(root mean square error，RMSE)、提高率(improvment，IP)3個方面對解算的結果進行評價。絕對誤差為

AE=|Hi-Li|

(12)

均方根的誤差表達式為

(13)

提高率表達式為

(14)

式中：Hi為參考真值；Li為解算的值；i=1，2,…,m，m為UWB采樣總數；AER為神經網絡補償之后的絕對誤差；AEI為無神經網絡補償的絕對誤差。

圖4給出了有RBF神經網絡輔助和無RBF神經網絡輔助的UWB/INS組合導航的軌跡與參考軌跡的整體比較，并在圖中依次標出UWB信號在157～162、205～215、270～285 s中斷時的局部軌跡。

圖4 整體軌跡

圖5為圖4中UWB信號中斷后軌跡的放大圖，可以看到RBF神經網絡輔助的組合導航方法的定位優勢非常明顯：如果采用無RBF神經網絡輔助的組合導航方法，在UWB信號中斷后不再對INS進行誤差補償，UWB/INS組合導航解算的定位結果迅速發散；而如果采用有RBF神經網絡輔助的組合導航方法，經過RBF神經網絡對發散的定位結果進行誤差補償，位置軌跡更接近參考的真值。

圖6～8分別為圖5(a)、圖5(b)、圖5(c)對應的位置絕對誤差圖，通過分析得：在UWB信號中斷5 s時，無RBF神經網絡輔助的組合導航的定位絕對誤差在x和y方向的最大值為0.11和0.08 m，均方根誤差為0.05和0.03 m；有RBF神經網絡輔助的組合導航的定位絕對誤差在x和y方向的最大值為0.08和0.07 m，均方根誤差為0.04和0.02 m，提高率分別為23.6 %和26.4 %，可知在UWB信號中斷5 s時2種組合導航方法的定位結果都比較好，其中有神經網絡輔助的定位精度比無神經網絡輔助的定位精度有小幅提升；在UWB信號中斷10 s時，無神經網絡輔助的定位絕對誤差在x和y方向的最大值為0.43和1.05 m，均方根誤差為0.18和0.51 m，有神經網絡輔助的定位絕對誤差在x和y方向的最大值為0.16 和0.18 m，均方根誤差為0.07和0.1 m，提高率分別為50.2 %和70.4 %，可知在UWB信號中斷10 s時，有神經網絡輔助的定位精度有較大提升；在UWB信號中斷15 s時，無神經網絡輔助的定位絕對誤差在x和y方向的最大值為1.15和2.18 m，均方根誤差為0.49和1.11 m，有神經網絡輔助的定位絕對誤差在x和y方向的最大值為0.64和0.67 m，均方根誤差為0.24和0.35 m，提高率分別為54.7 %和59.6 %，可知在UWB信號中斷15 s時2種組合導航方法的定位誤差都較大，雖然有神經網絡輔助的定位精度更高，但相對UWB在視距環境下的定位精度，有神經網絡輔助的組合導航的定位精度已不能滿足人們的定位要求。

圖5 UWB信號中斷的局部軌跡

圖6 UWB信號中斷5 s的絕對誤差

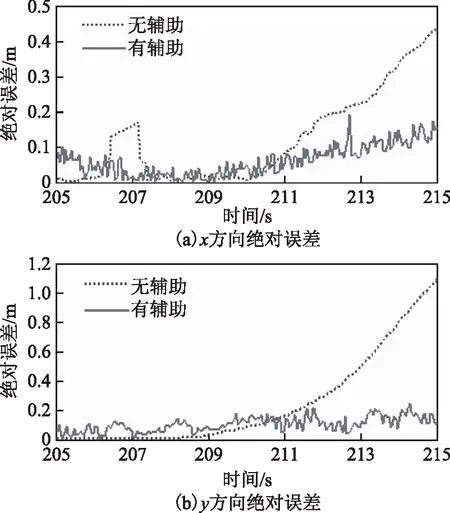
圖7 UWB信號中斷10 s的絕對誤差

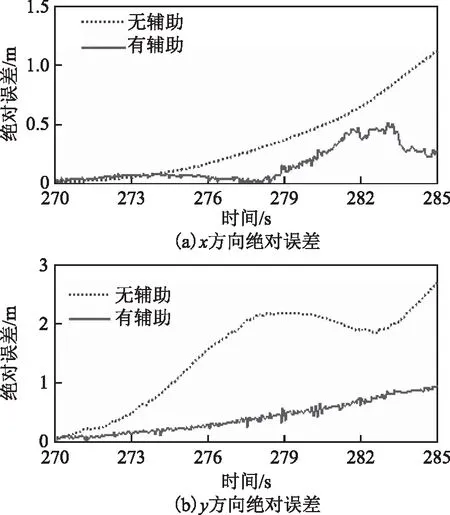
圖8 UWB信號中斷15 s的絕對誤差

綜合上述分析可知：要保證定位均方根誤差不大于10 cm，UWB信號中斷不能超過10 s。另外從圖6～8中可以發現，隨著UWB信號斷開時間的增加，無神經網絡輔助的組合導航的定位絕對誤差加速增大，雖然經過RBF神經網絡補償的定位絕對誤差也開始增大，但增大的速率遠慢于無神經網絡補償解算的結果。

4 結束語

本文的目的是在不增加硬件成本的基礎上提出一種UWB/INS組合導航方法以提高在UWB信號中斷后的定位精度。為此，設計了一種RBF神經網絡輔助的導航算法來補償在UWB信號中斷后的UWB/INS組合導航的定位誤差，這種方法不需要像傳統的UWB和INS數據融合方法一樣要對各個傳感器的隨機誤差建模，利用RBF神經網絡訓練過程中存儲的知識對發散的定位結果進行誤差補償，就能為載體提供持續和較高精度的定位信息。實驗結果表明在UWB信號中斷0～15 s的時間里，所提方法都能夠有效提高定位精度。下一步工作包括根據儀器的參數和實際經驗提前求得神經網絡的各項參數以減少訓練的時間，并通過實際的車載數據進一步驗證RBF神經網絡輔助的UWB/INS組合導航算法的有效性。