基于隨機延誤情景的城軌網絡末班車時刻表調整模型

徐文愷，趙 鵬，寧麗巧，張 輝

(1.北京交通大學 交通運輸學院，北京 100044；2.山東建筑大學 交通工程學院，山東 濟南 250101)

城市軌道交通網絡末班車時刻表調整是指網絡中某線路末班車發生延誤時，通過調整末班車在換乘站的到發時刻，協調不同線路末班車在換乘站的銜接關系，實現一定目標下的系統最優。末班車間的銜接關系決定著城市軌道交通網絡在運營結束階段的換乘可達性[1]，在末班車運行延誤的條件下，網絡換乘可達性的變化會導致換乘乘客錯失計劃換乘，從而無法經由城市軌道交通網絡完成出行。因此，當末班車運行發生延誤時，有必要結合乘客需求和運營管理要求，及時調整網絡末班車時刻表，盡可能保證乘客的正常出行。隨著乘客對城市軌道交通系統服務水平要求的提高，該問題具有重要的研究價值和現實意義。

目前，國內外學者主要從末班車換乘銜接的角度研究網絡末班車時刻表問題，期望得到一個更優的網絡末班車計劃時刻表，但針對網絡末班車時刻表調整問題的研究較少。文獻[2]根據網絡中各線路和換乘站的重要度系數確定網絡的主協調線路和換乘站，以乘客在換乘站的總候車時間最小化為目標，根據重要度從大到小依次求出各線路末班車在各換乘站的到發時刻。文獻[3]通過選取主導銜接關系和主協調換乘站，以成功實現換乘的末班車乘客數量最大化為目標構建網絡末班車銜接方案優化模型，并將問題轉化為最大生成樹問題，借鑒Kruskal算法推算出協同優化的網絡末班車時刻表。文獻[4]結合路徑選擇模型，以乘客換乘等待時間最小化和換乘失敗乘客數量最小化為目標，設計一種遺傳算法求解出各線路末班車在始發站的發車時刻。文獻[5-6]通過選取網絡的關鍵換乘方向，以乘客換乘等待時間最小化和成功換乘銜接關系數量最大化為目標構建網絡末班車協同優化模型。文獻[7]設計一種啟發式算法優化網絡末班車時刻表，案例分析表明該算法明顯優于模擬退火算法和遺傳算法。文獻[8]建立以乘客總體換乘不滿意度最小、換乘成功的乘客數量最多和各線路方向末班車結束運營時間最早為目標的確定環境下的末班車時刻表銜接優化模型，設計NSGA-II算法求解。文獻[9]從網絡末班車時段出發，構建以總乘客換乘等待時間最小化為目標的末班車時段時刻表協同優化模型。

總之，目前絕大多數關于網絡末班車問題的研究集中于網絡末班車計劃時刻表的編制優化，很少涉及網絡末班車運營過程中遭遇突發事件延誤后的時刻表調整問題。但無論是網絡末班車時刻表協調優化問題還是網絡末班車時刻表調整問題，換乘乘客都是研究的重點。本文從乘客的角度出發，以實現換乘的乘客數量最大化為目標；從運營的角度出發，以調整時刻表與計劃時刻表的偏離程度最小化為目標構建網絡末班車時刻表調整模型。通過ε-constraint法[10-11]，將模型轉化為單目標混合整數規劃模型，并通過不斷調整ε取值，求出相應的近似Pareto最優解，即網絡末班車的時刻表調整方案。

1 網絡末班車時刻表調整模型

在實際運輸生產過程中，當發生列車運行延誤時，調度管理人員往往采用趕點、跨站停車、扣車、小交路等措施使列車盡快恢復正點運行，而較少考慮對乘客的影響[12-14]。此外，既有研究中的末班車時刻表模型大多是基于預先確定的主協調線路或關鍵換乘方向。本文所構建的模型結合網絡末班車間換乘客流分布，不選擇主協調線路或關鍵換乘方向，從乘客以及全局優化的角度，協調延誤條件下各線路末班車間的銜接關系。

1.1 符號和變量

模型的符號和參數定義如下：

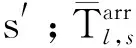
模型的決策變量定義如下：

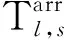
1.2 末班車銜接關系

根據各線路末班車在換乘站的實際到發時刻，每一個銜接關系c存在以下兩種情景：

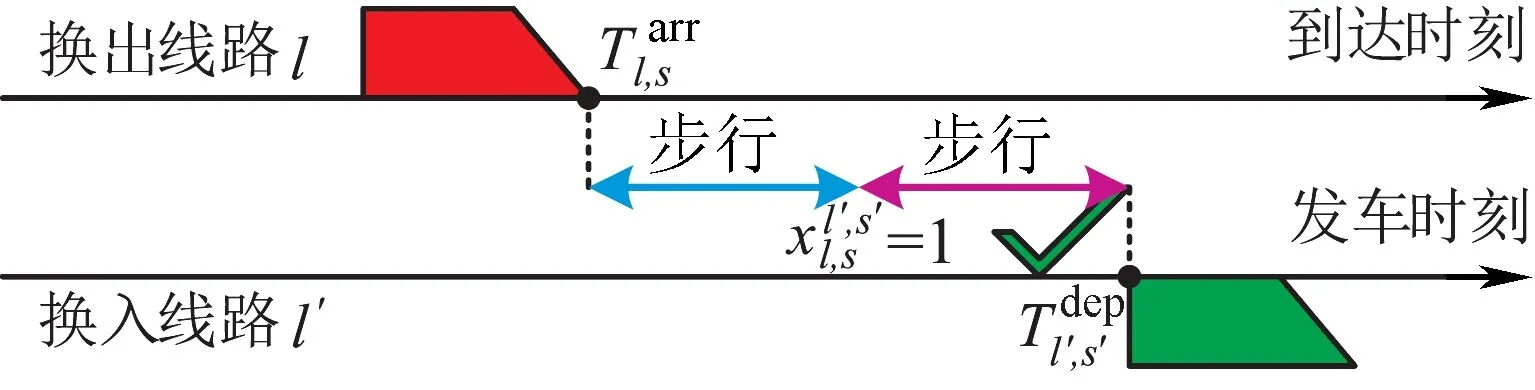
圖1 換乘銜接成功

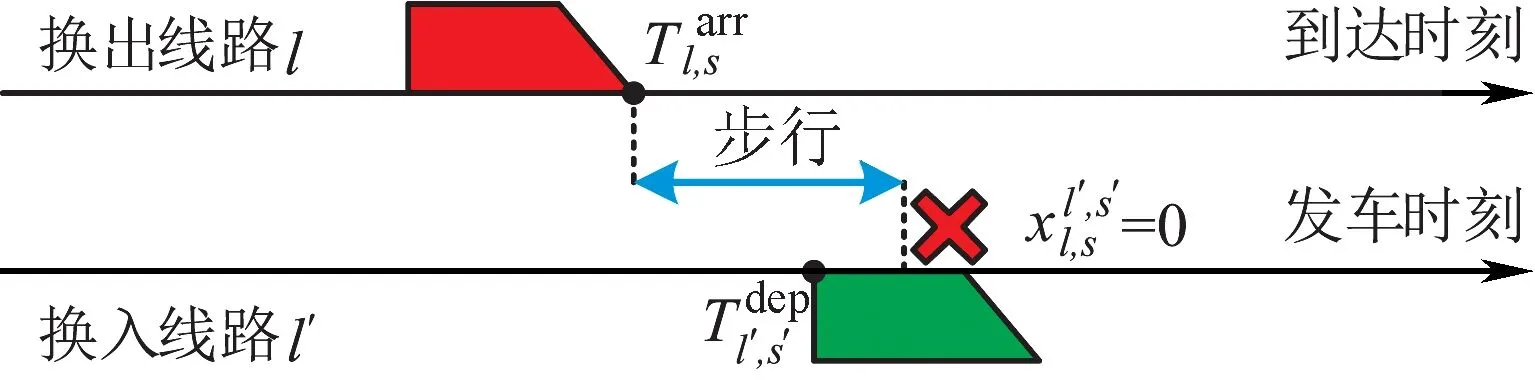
圖2 換乘銜接失敗

( 1 )

( 2 )

( 3 )

1.3 優化模型

針對網絡末班車問題，網絡換乘可達性對乘客出行有著十分重要的影響。本模型從乘客和運營兩個角度出發，建立目標函數。

( 4 )

( 5 )

式( 4 )從乘客的角度出發，以換乘成功乘客數量最大化為優化目標。從運營的角度出發，當發生列車運行延誤時，調度管理人員須盡快使列車運行恢復至計劃時刻表，因此，式( 5 )表示調整時刻表與計劃時刻表的偏離程度最小化。該目標也有利于降低調整時刻表對非換乘乘客的影響。

模型約束如下：

s.t.

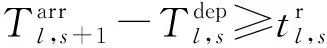
( 6 )

( 7 )

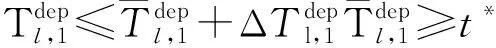
( 8 )

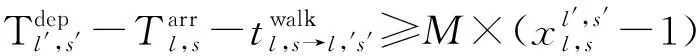
( 9 )

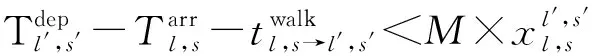
(10)

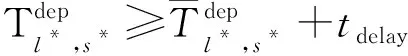
(11)

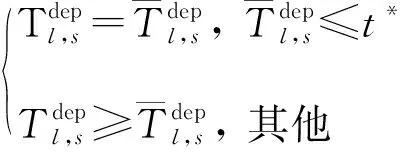
(12)

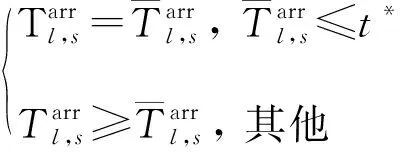
(13)

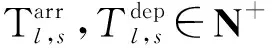
(14)

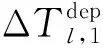
式( 6 )、式( 7 )為安全性約束，各線路末班車在區間的運行時間不得小于最短運行時間，在車站的停站時間不得小于最短停站時間[15]。式( 8 )為靈活性約束，對于發生列車延誤事件后還未從始發站發出的末班車，允許調整其在始發站的實際發車時刻。式( 9 )、式(10)即式( 2 )、式( 3 )，用于判斷各線路末班車在換乘站的銜接關系是否成立。式(11)為初始延誤約束，用于輸入列車的延誤時間及位置。式(12)～式(14)為實際問題決策變量約束。

2 模型求解

本文所構建的雙目標優化模型旨在最大化換乘成功乘客數量的同時最小化調整時刻表與計劃時刻表的偏離程度，期望得到一組近似Pareto最優解以體現兩個目標函數之間的均衡，可以直觀地作用于調度管理人員的決策過程。多目標優化模型求解時需要轉換為單目標模型，而常用的權重系數法存在權重系數難以確定的問題。因此，本文采用ε-constraint法求解近似Pareto最優解。

選取目標函數式( 5 )作為ε-constraint，將式( 5 )轉換為式(15)。

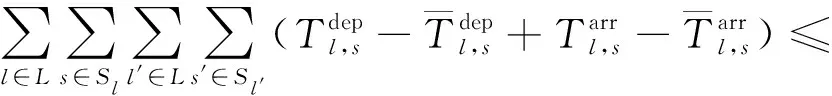
(15)

式中：F*為僅考慮目標函數式( 5 )的條件下模型求得的最優值；ε為調度管理人員對調整時刻表與計劃時刻表偏離程度的容忍度，0≤ε≤εmax，εmax為調度管理人員對偏離程度的最大容忍度。

采用ε-constraint法，將本文所構建模型轉換為以換乘成功乘客數量最大化為目標的單目標混合整數線性規劃模型(MILP)，通過改變ε的取值，使用Cplex軟件編程求解出相應的近似Pareto最優解。模型的求解過程如圖3所示。

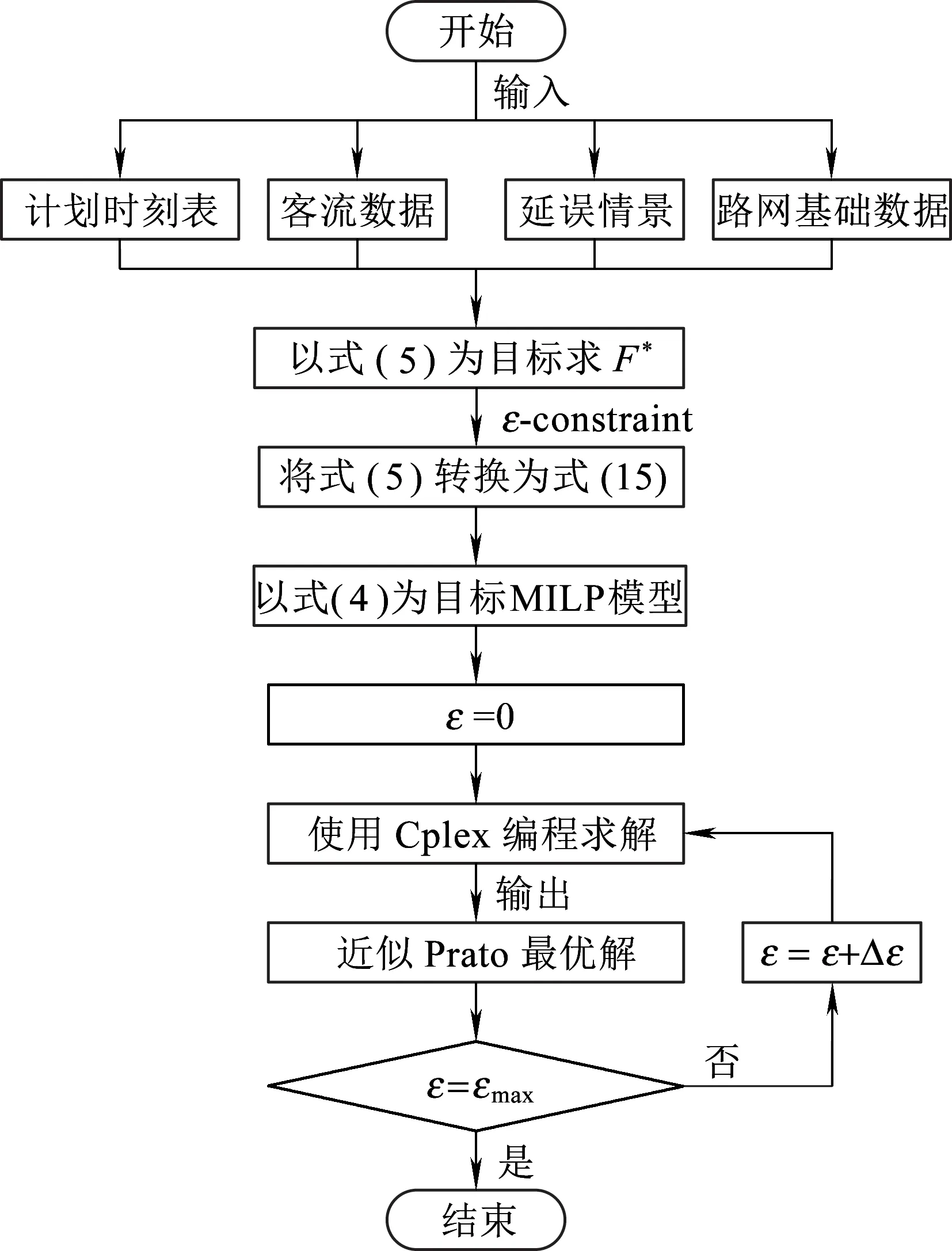
圖3 模型求解

3 案例分析

本文以北京地鐵網絡為研究對象，驗證模型的有效性。截至2017年6月底，除機場線外，北京地鐵網絡共包含18條雙線線路，53座換乘站，路網結構如圖4所示。由于客流特征等因素的不同，不同的線路有不同的運營時間范圍，各線路的末班車計劃時刻表詳見北京地鐵官方網站。

圖4 北京地鐵路網(不包括機場線)

換乘客流量是決定一個末班車銜接關系是否要滿足的關鍵因素。但清分后的地鐵自動售檢票(AFC)數據只能給出一段時間內每一個換乘方向的換乘客流量，無法準確得到來自某列車的換乘客流量。因此，在現有的技術條件下我們無法準確獲得來自末班車的換乘客流量。本文以各線路最后30 min的AFC數據為基礎生成在各個換乘站從末班車下車去往其他線路的換乘客流量。由于本文所提出的模型并不需要提前選取實際路網中的主協調線路或關鍵換乘方向，所以基于AFC數據生成的換乘客流數據雖然與實際不符，但并不影響驗證模型的有效性。

3.1 隨機延誤情景分析

為驗證模型的有效性，本文隨機生成若干延誤情景，每個延誤情景隨機選擇北京地鐵網絡中的某條線路，假設該線路的末班車發生延誤，延誤時間設置為3～10 min。具體延誤情景見表1。

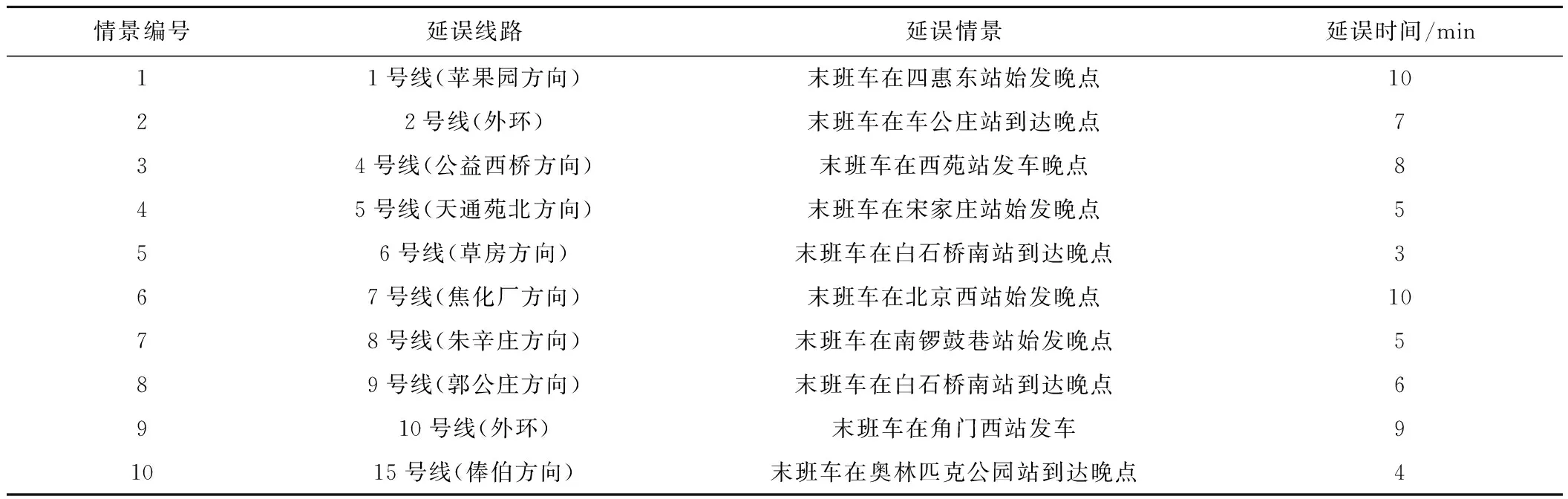
表1 延誤情景

通過在3.1 GHz CPU, 8 GB RAM臺式電腦上使用Cplex軟件編程求解每一個末班車延誤問題，所有問題均在2 s內求得最優解，可以滿足實際運輸生產過程中實時性的要求。為驗證模型的有效性，設置對比方案，各方案詳細求解結果見表2，括號中的百分比代表相對于方案A的提高比例。

方案A：列車運行延誤后不進行任何調整，仍然按照計劃時刻表中的區間運行時間和停站時間運行。

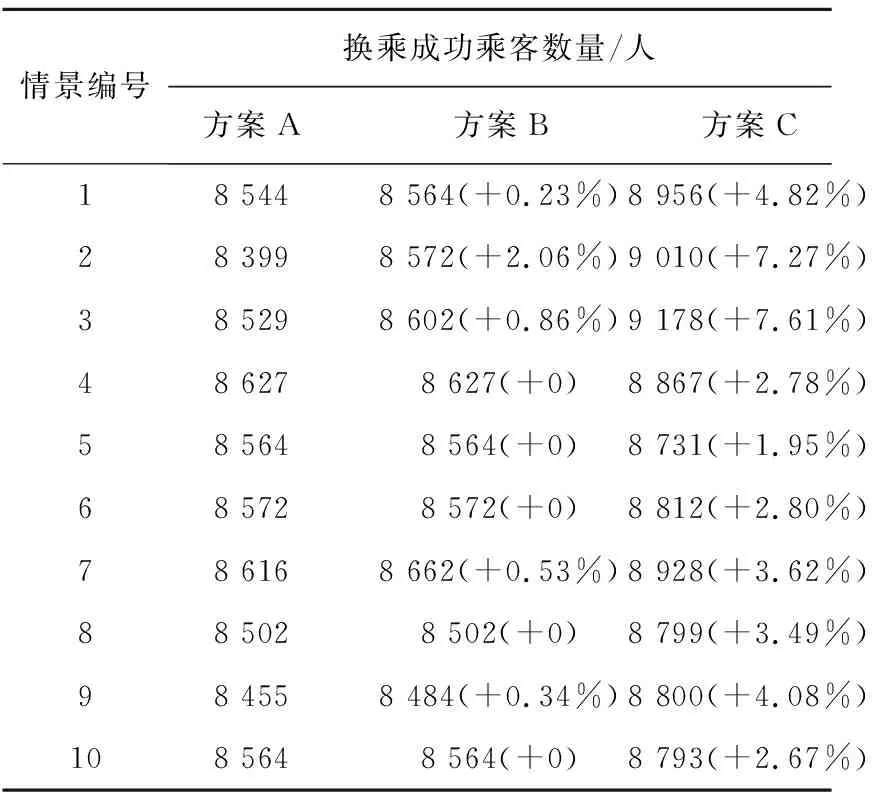
表2 求解結果

求解結果表明，在任意延誤情景下，方案B都不比無調整的方案A差，而方案C都要優于方案A。這也說明在末班車延誤的條件下，調度管理人員一定要及時響應，科學調整末班車時刻表，保證系統的服務水平。相對于方案B，方案C的優化效果更加明顯：在換乘成功乘客數量上，方案C與方案A相比有1.95%～7.61%的增長，而方案B最高也僅有2.06%的提高。方案C可以明顯提高末班車延誤后系統的服務水平，更好地保證乘坐末班車換乘乘客的正常出行。求解結果證明了本文所提出方法的準確性和有效性。

3.2 近似Pareto最優

Pareto最優是指資源有限的條件下一種理想的資源分配狀態，當多目標模型中某個目標函數的函數值變優時必然會導致其他目標函數的函數值變差，此時對應的解即Pareto最優解，Pareto最優解也是資源利用效率最高的解。在給定路網及延誤情景的條件下，調度管理人員對調整時刻表與計劃時刻表偏離程度的容忍度越高，調整時刻表與計劃時刻表的偏離程度越大，相反，各線路末班車在換乘站實現換乘銜接的可能性越大。本文以延誤情景1為例，通過改變ε的取值(εmax=0.5，Δε=0.05)，求出相應的近似Pareto最優解，見表3。繪制換乘成功乘客數量與偏離程度散點圖，如圖5所示。可以發現一個明顯的趨勢：隨著偏離程度的增加，換乘成功乘客數量明顯提高。而每一個近似Pareto最優解代表一個時刻表調整方案，調度管理人員在實際運輸生產過程中要權衡各方案的優劣，并選擇一個最有利的方案。

表3 近似Pareto最優解(情景1)

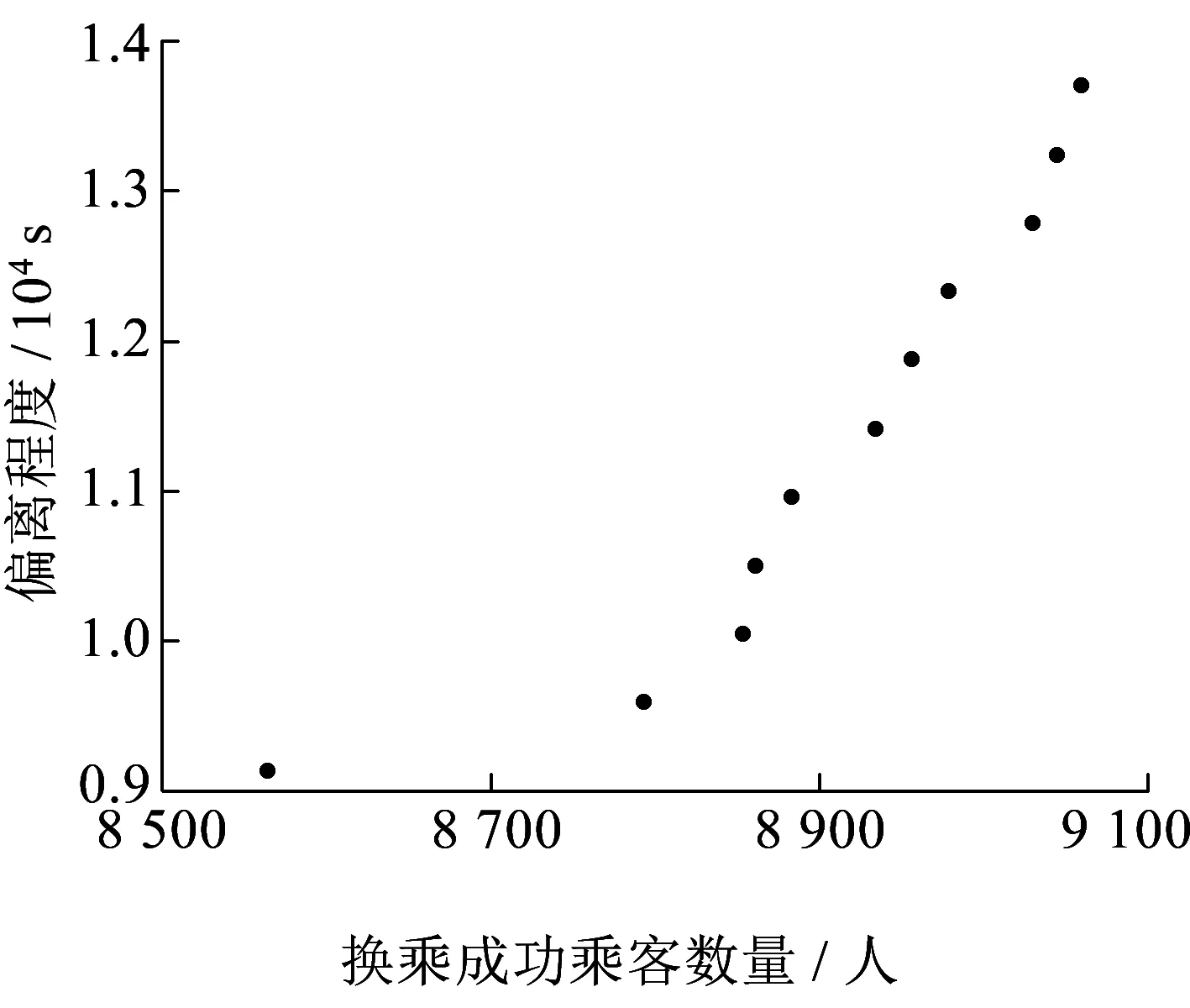
圖5 換乘成功乘客數量與偏離程度散點圖

為輔助調度管理人員決策，本文引入參數總運行時間tTotal，是指所有線路末班車從始發站到終點站的運行時間之和。

(16)

根據式(16)計算無調整方案A的總運行時間為99 900 s，計算各近似Pareto最優解的總運行時間見表3。以高偏離容忍度(ε=0.5)求出的時刻表調整方案，換乘成功乘客數量比方案A增加515 (+6.03%)人，而總運行時間僅增加1 227 s。考慮到北京地鐵包括18條雙線線路、36列末班車，平均每列末班車運行時間僅增加34 s，幾乎可以忽略不計。這也說明調整時刻表對非換乘乘客的影響較小。在其他延誤情景下，也得到了相似的結果。因此，當網絡中發生末班車運行延誤時，調度管理人員應該更多的從乘客的角度出發，選擇換乘成功乘客數量更多的時刻表調整方案。

4 結論

在網絡化運營條件下，換乘銜接質量是衡量城市軌道交通服務水平的重要指標。而針對末班車銜接優化問題，末班車銜接合理與否直接關系到網絡換乘可達性的高低。一旦換乘乘客錯過其銜接線路的末班車，則意味著該乘客無法通過軌道交通系統完成出行，將嚴重降低系統的服務水平。

本文針對城市軌道交通網絡末班車延誤問題，以換乘成功乘客數量最大化和調整時刻表與計劃時刻表偏離程度最小化為目標構建了末班車時刻表調整模型，并采用ε-constraint法將模型轉換為單目標混合整數線性規劃模型，使用Cplex軟件可快速求出最優解。在以北京地鐵網絡為研究對象的案例分析中，隨機生成末班車延誤情景，使用模型求解出的調整時刻表能夠使換乘成功乘客數量增加1.95%～7.61%。在給定延誤情景的條件下，改變ε取值，可使用模型求得相應的近似Pareto最優解，為調度管理人員提供決策支持。

案例分析結果表明，隨著調整時刻表與計劃時刻表偏離程度的增加，換乘成功乘客數量明顯增加，而末班車的運行時間沒有明顯變化：ε=0.5時，換乘成功乘客數量增加了6.03%，而平均每列末班車的運行時間僅增加了34 s，對非換乘乘客影響較小。因此，隨著乘客對軌道交通系統服務水平要求的日益提高，當網絡中發生末班車延誤時，調度管理人員應該在整合分析歷史客流數據、末班車延誤數據的基礎上，合理確定ε取值，選擇更有利于乘客的末班車時刻表調整方案。