非線性波動Zakharov方程組的多辛Fourier擬譜算法

張 星 單雙榮 徐金平

（1.福建生物工程職業技術學院公共基礎部，福建 福州 350002；2.華僑大學數學科學學院，福建 泉州 362021；3.閩南理工學院，福建 石獅 362021）

1.引言

文章考慮如下非線性Klein-Gordon-Zakharov（簡稱KGZ）方程組

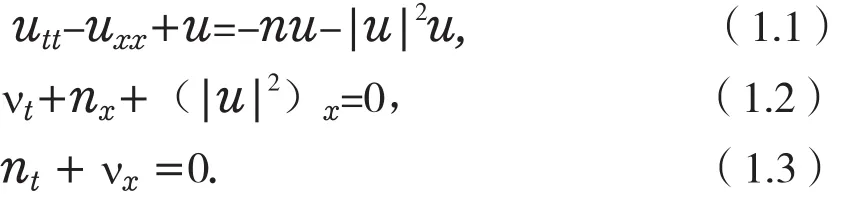
是描述在等離子體中Langmuir波與離子聲波交互作用的一個經典模型。［1］在數學上，該方程表現為含有兩個未知函數u（x，t）和n（x，t）的耦合方組。其中u（x，t）是復函數，而n（x，t）則是實函數。

文章在xL≤x≤xR，0≤t≤T上對帶有如下初邊值條件

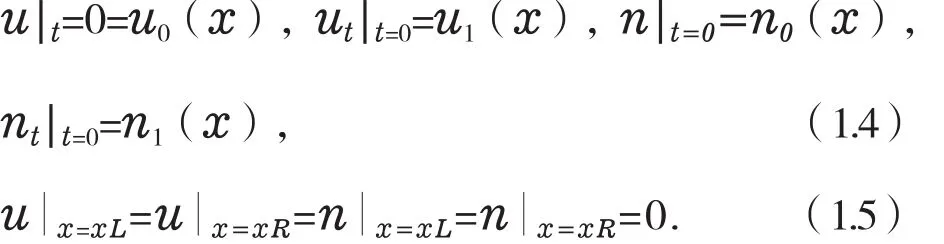
的一維KGZ方程從辛幾何的角度去考慮，其中函數u（x，t）為復值函數，函數n（x，t）為實值函數，u0（x），n0（x），u1（x），n1（x），均為已知函數。先把方程組引入正則動量轉化成多辛形式的方程組，再對得到的多辛方程組用Fourier擬譜方法離散，可以得到其多辛Fourier擬譜格式，最后通過數值試驗驗證多辛Fourier擬譜格式（3.2.3）滿足二階精度0（h2+τ2），并且能長時間保持孤立波傳播。

2.非線性KGZ方程組的多辛形式及其守恒律

利用方程（1.2）和（1.3），可以消去ν（x，t）得到下面的方程組

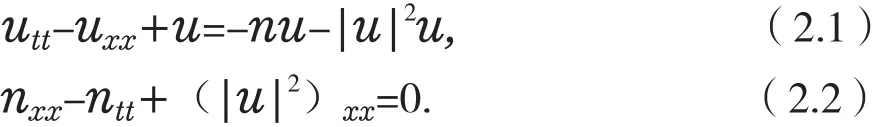
下面考慮KGZ方程組（2.1），（2.2）的多辛結構及其相關守恒律。

令u（x，t）=P（x，t）+iq（x，t），則方程組（2. 1），（2. 2）可化為

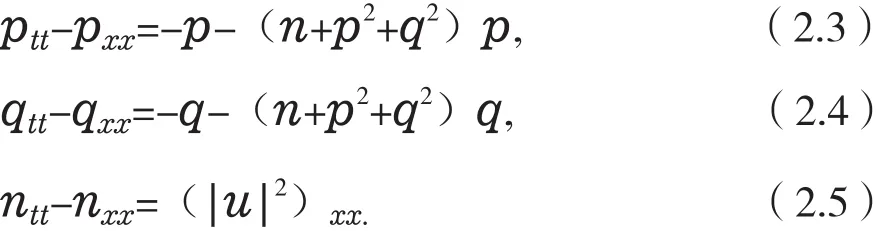
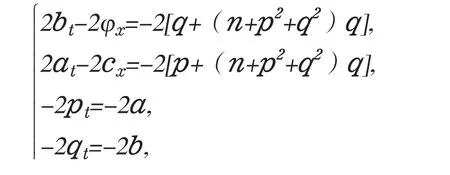
引入正則動量pt=a，qt=b，px=c，qx=φ，nt=νx，wx=ν.得到KGZ方程組（2. 1），（2. 2）的多辛方程組在不同時刻的孤立波的傳播情況，圖5和圖6分別給出|u|和n在步長（h，τ）=（0.05，0.01）時多辛Fourier擬譜格式得到的孤立波模擬，多辛Fourier擬譜格式能很好的模擬孤立波的傳播。

圖3和圖4分別給出|u|和n在不同時刻的孤立波的傳播情況

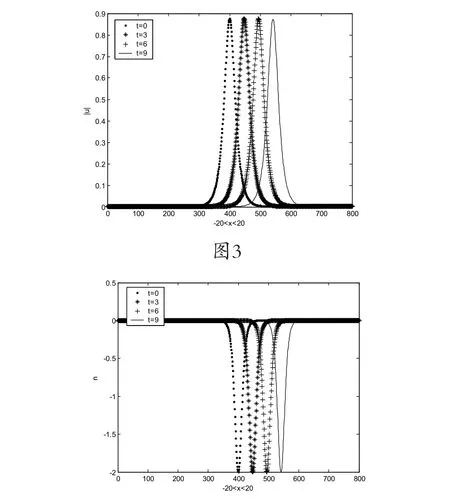
圖4

圖5 和圖6分別給出|u|和n在步長（h，τ）=（0.05，0.01）時的孤立波模擬

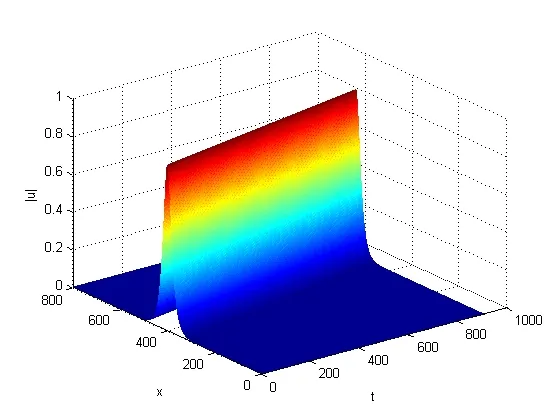
圖5

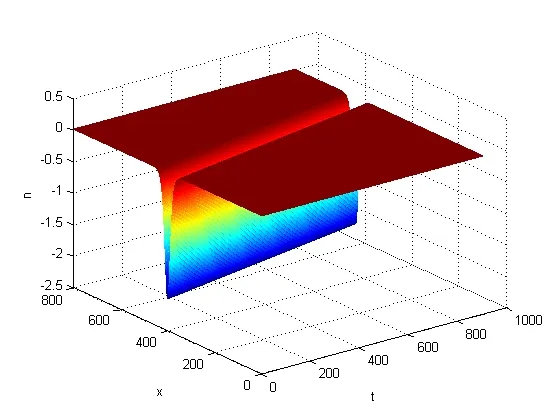
圖6

綜上數值實驗由表1-表3，圖1-圖6可以看出：

（1）通過多辛Fourier擬譜格式（3.2.3）計算出的數值解很好的逼近了精確解，并且滿足二階收斂性。

（2）多辛Fourier擬譜格式（3.2.3）能夠長時間的模擬孤立波.經過了長時間的數值模擬后波的各個要素，如：形狀、振幅等，能夠很好的保持，長時間誤差較小。

（3）多辛Fourier擬譜格式（3.2.3）在不同網格比下，能夠很好的模擬孤立波的傳播。

由此驗證了文章構造的多辛Fourier擬譜格式（3.2.3）是正確有效的。