數據挖掘在“拍照賺錢”任務定價中的應用

程子庚　趙珂瑤　李倩　李藝璇

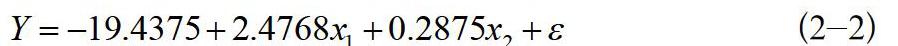
摘要：“拍照賺錢”是移動互聯網下的一個自助式服務模式。APP用戶會員通過完成需要拍照的任務，賺取對任務所標定的酬金。因此，任務定價是該平臺運行的核心要素。本文利用數據挖掘的手段探索位置、任務、會員等相關因素與任務定價乃至任務認領完成情況的量化關系，實現統計建模，并優化了任務定價分配方案。

關鍵詞：統計建模；任務定價；數據挖掘

中圖分類號：TP391；F274 文獻標識碼：A 文章編號：1007-9416（2018）04-0114-02

1 問題分析

1.1 模型背景

“拍照賺錢”是移動互聯網下的一種自助式服務模式。用戶下載APP，注冊成為APP的會員，然后從APP上領取需要拍照的任務，賺取APP對任務所標定的酬金。這種基于移動互聯網的自助式勞務眾包平臺，為企業提供各種商業檢查和信息搜集，相比傳統的市場調查方式可以大大節省調查成本，而且有效地保證了調查數據真實性，縮短了調查的周期。因此APP成為該平臺運行的核心，而APP中的任務定價又是其核心要素。如果定價不合理，有的任務就會無人問津，而導致商品檢查的失敗。

1.2 模型假設

（1）本文所提供的數據均真實可靠；（2）題目中位置均忽略高度屬性，即位置之間的距離均采用二維平面距離進行計算；（3）針對短時間同一個模型，認為其社會環境系統是不變的；（4）針對短時間內的會員信息數據，認為會員的數量、地理位置、信譽值等相關屬性均保持不變；（5）忽略行業內部不正當競爭對模型產生的畸形影響；（6）每一個位置視為一個質點，且不考慮道路阻塞的情況。

1.3 模型分析

此題本質上是一個基于人機交互系統的計算任務定價的數據建模問題。用戶首先注冊成為會員，并上傳自己的GPS經緯度信息，獲取初始信譽值。會員根據個人情況，從數據庫發布的任務信息中預訂并完成任務來賺取酬金。系統則根據累計的交易情況、會員的反饋不斷更新數據庫信息，并以此不斷地調整任務價格以及適當地采取任務聯合打包的方式提高會員完成任務率。

2 模型建立與求解

2.1 任務定價規律的研究

2.1.1 模型的建立

本文以經度和緯度以及其相應的任務標價的觀測數據為出發點，通過對這種數據結構的分析研究，尋找變量之間的依賴關系。按回歸模型類型可以將其劃分為線性回歸分析和非線性回歸分析。為將問題簡化，即認為該問題是一個二元線性回歸問題，并主要采用二元線性回歸分析的方法來初步研究項目的任務定價規律。

設因變量定價Y與2個解釋變量經緯度x1和x2之間具有線性相關關系，則有（2-1）：

其中，是殘差。

2.1.2 模型的求解

利用計算機求解該模型，得到模型的回歸系數估計值及其置信區間（置信水平）、檢驗統計量R2，F，p，s2的結果如表1。

得到線性回歸關系的表達式為（2-2）：

（2-2）

2.1.3 結果分析

表1顯示，R2=0.0148指因變量y的1.48%可由模型確定，F值并沒有遠遠超出臨界值，s2作為方差也相對較大，所以該線性回歸并不合理。

一般在生產實踐和科學研究中，人們得到了參數x=（x1，…，xn）和因變量y的數據，需要求出關系式y=f（x），這時就可以用到回歸分析的方法。進行線性回歸時，有三個基本假定：（1）待定參數是線性關系；（2）殘差是獨立的；（3）殘差滿足標準正態分布。

因變量Y的值是隨每組觀察值（x1，x2）而變化的，可以看出，并非所有殘差都在0點附近均勻分布，即存在較多高杠桿點，故數據中存在強影響點、異常觀測點。根據以上分析得出使用線性回歸來描述標價與任務位置之間的關系并不合理，于是采取數據建模的方法，直接對不同價格的位置進行聚類來分析標價與任務位置的關系。在具體求解過程中采用了K-Means方法。通過對標價的數值大小將其聚類為4類。標價與位置并未呈現一個均勻的、有規律性的線性分布。因此，使用簡單的線性回歸對任務標價進行研究是不可行的。

2.2 任務未完成原因的分析

任務完成情況與任務位置和任務標價有著顯著的關系。結合實際情況分析得出如下結論：

（1）未完成的任務在地理位置上呈集中分布，所以任務的完成率跟地理位置有明顯的相關關系。未完成的任務主要分布在中心點分別為（22.60，114.00）、（23.18，113.11）、（23.05，113.10），半徑分別為0.2、0.1、0.05的鄰域中；（2）已完成任務的定價分布跨度較大，在45和90之間都有很顯著的分布傾向，期望Ex位于70的右側；未完成的任務定價，期望Ex位于70的左側。所以任務的完成率與任務的定價有關；（3）任務未完成，一部分原因是任務點在較偏遠區域，另一部分原因是雖然任務點在中心區域，但任務量多，標價較低，對會員的吸引力不足；（4）任務未完成還可能與會員所在地區有關。定義一個比值即任務數與會員數的比例來衡量該地區任務的擁擠程度：比值越大，任務越擁擠，完成情況越不理想；反之則完成情況理想。

3 模型優化

3.1 打包優化指標的提出

配額ReLU（修正線性單元）系數：會員信譽值與會員的任務預訂限額并非簡單的線性關系，由相關背景知識可得，新用戶只能預定一個任務，預定的數量隨信譽的提高而增長，因此，這里引入配額ReLU系數，由式（3-1）分段表示： （3-1）

鄰域內會員活躍度：第j個會員在點a的領域內配額數與該鄰域任務總數量的比值。

預訂限額與會員的信譽有關，原則上，會員的信譽越高，獲得的參與任務的機會也就越高，信譽高的會員可以拿到更多的酬金。即任務標價、會員活躍度和任務完成率是一個三維閉循環關系。

鄰域內任務密度：范圍內的任務總和形成的密度值

3.2 貪心算法分配打包任務

改進后的定價方案可以提升任務執行的成功率，但是部分任務分布不均勻，任務附近會員人數、會員預定任務限額和信譽度都相差較大，導致部分區域的任務因分配方式不合理而無法成功完成，部分任務被附近較多的會員爭相選擇。本文考慮將任務聯合在一起打包發布，如圖1紅色表示被納入到已打包集合內的任務點，藍色表示距離該集合最近的任務點。采用貪心算法，每一步都計算得到當前最優解納入集合，從而解決問題。

為了降低公司成本，本文設計了打包后價格調整方案，考慮適當降低打包后的任務標價：

其中，fnew為調整后的任務標價，Cl為會員預定的從小到大重新排列后的第l個任務的標價，Limit為會員預定任務的限額。

3.2.1 目標函數和約束條件的確定

該模型是一個雙目標模型，以距離最近為第一優化目標，將距離最近的5個任務打包聯合發布，目標函數為（3-6）；分析上述指標的含義并結合模型一與問題二的結論，以定價最低為第二優化目標，目標函數為（3-7）。

根據以上目標建立優化模型，在題目給定的可行域中尋求最優解。

約束條件（3-8）：公司提供酬金的最高預算為budget；

約束條件（3-9）：打包后的會員活躍度不能低于當前活躍度；

約束條件（3-10）：打包后的完成率期望不能低于當前期望。

3.2.2 打包模型的求解

根據上述模型，利用計算機求解。得到打包之前，任務未完成區域大致為3類，打包之后未完成任務的數量明顯減少，減少了39.94%，聚簇程度明顯降低，且僅聚為2類。

參考文獻

[1]杜劍平，韓中庚.“互聯網+”時代的出租車資源配置模型[J].數學建模及其應用，2015，4（4）：40-49+85.

[2]張媛.大眾參與眾包的行為影響因素研究[D].東北財經大學，2011.

[3]姜啟源.多屬性決策中幾種主要方法的比較[J].數學建模及其應用，2012，1（3）：16-28.