采用幅度相移鍵控調制的分層空間調制算法
李云風, 王磊, 王志成
(西安交通大學電子與信息工程學院, 710049, 西安)
多輸入多輸出(MIMO)技術既可以通過空間復用來提高系統的容量,又可以通過空間分集來提升系統的可靠性,因而近年來獲得了廣泛的研究。但是,MIMO技術在帶來各種增益的同時,也存在著系統復雜度高和硬件實現中射頻單元成本高等一些缺陷。隨著MIMO傳輸技術的深入研究,Mesleh等人于2008年提出了空間調制(SM)技術[1],創造性地提出了多天線調制中不僅可以利用幅度相位調制(APM)符號傳輸信息,而且可以利用天線索引號來傳遞額外的信息。SM技術在同一個時隙中只需激活一根天線來發送信號,其余天線保持靜默狀態,因而能夠有效地避免MIMO方案中諸如天線間同步、信道間干擾以及射頻鏈路多等問題。文獻[2-3]提出的空移鍵控(SSK)技術作為一種簡化的SM傳輸技術,僅利用空間維度攜帶信息,具有較低的檢測復雜度。然而,SM/SSK的頻譜效率都與發射天線數呈對數關系,因而不能獲得很高的頻譜效率。為了提高SM的頻譜效率,很多研究者提出了不同的改進方案。文獻[4-7]通過在發射端采用多根發射天線組合的方式來發送信號,分別提出了廣義空移鍵(GSSK),廣義空間調制(GSM)和多天線激活-空間調制(MA-SM)。GSSK方案通過同時激活多根天線,僅利用空間維度來增加系統的頻譜效率。MA-SM方案通過在每一個時隙同時激活多根發射天線來傳輸不同的調制符號以提高系統的頻譜效率。文獻[8]通過額外的調節空間維度,將復信號分解然后擴展到同相和正交維度,提出了正交空間調制(QSM),實現了發射天線同步并增強了傳輸性能。文獻[9]通過擴展星座中星座點的個數,提出了一種擴展空間調制(ESM)方案,有效地提升了系統的頻譜效率,并在文獻[10]中進行了完善。文獻[11]為了更好地利用空間維度來發送信息,提出了分層空移鍵控(LSSK)方案,利用分層結構,通過增加SSK傳輸層的數目來提高SM的頻譜效率。
本文為了提高SM的頻譜效率,提出了一種基于APSK的分層SM(LSM)算法。LSM算法通過不同層發射來自不同振幅的PSK星座點來發送多層SM信息,靈活地調節激活天線的個數,使SM的頻譜效率隨著層數的增加呈線性增長。此外,為了進一步降低系統的誤比特率(BER),對于一個特定的MIMO系統,本文提出了一種有效的算法,來確定APSK的內外環幅度比。最后,本文通過接收端將激活天線索引號和調制符號單獨檢測,提出了一種低復雜度譯碼算法,可以有效地降低譯碼復雜度。
1 系統模型
對于一個具有Nt根發射天線和Nr根接收天線的MIMO系統,設其在一個時隙發射Nt×1維信號s,則Nr×1維接收信號y可表示為
式中:ρ是發射端總的發射功率;L表示總層數,1≤L≤Nt;H和n分別表示Nr×Nt維的信道矩陣和Nr×1維加性高斯白噪聲(AWGN)向量,H和n中的元素均服從均值為0、方差為1的獨立復高斯分布。
2 本文所提LSM算法
2.1 LSM算法系統模型
考慮一個采用LSM調制的MIMO系統,L層的LSM發送信號s表示為
s=[0 …xi…xL…x1… 0]T
(2)
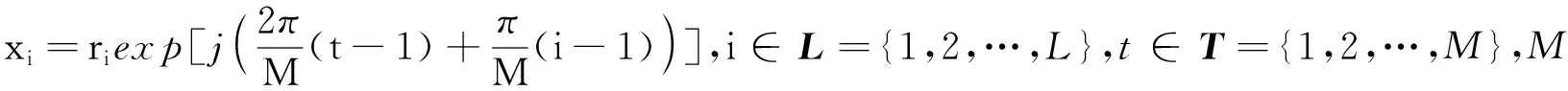
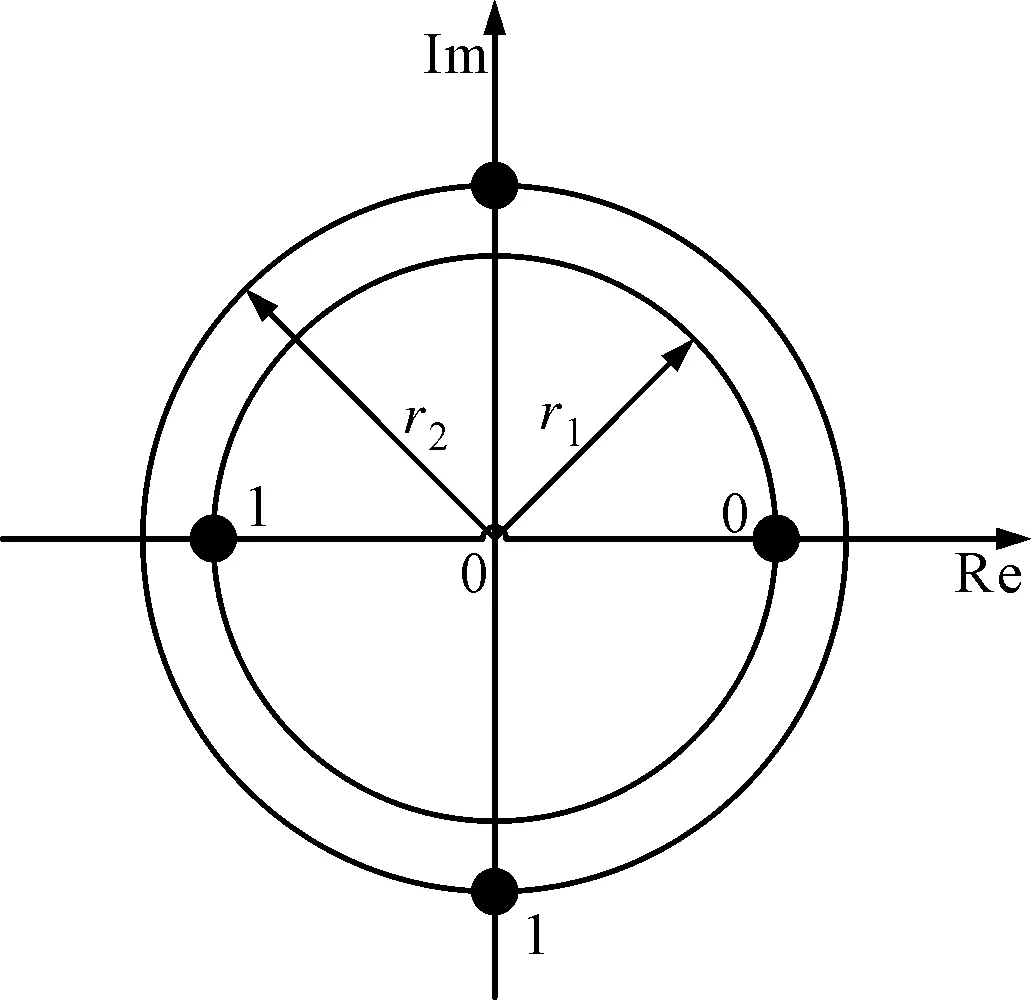
圖1 2-APSK調制的星座圖
圖1給出了M=2、L=2時的APSK調制的星座圖。第1層發送幅度為r1的PSK調制符號,第2層發送幅度為r2的PSK調制符號,并且相比于幅度為r1的PSK星座旋轉了π/Mrad。
因為每根激活天線發送一層SM信號,每層發送比特數為lbQ+lbM,所以LSM的頻譜效率為L(lbQ+lbM)。其中Q是每層天線個數,并且有
Nt=Q+L-1
(3)
表1給出了在不同發射天線數下,M=4,L=2時,本文LSM算法與其他幾種算法頻譜效率的比較。
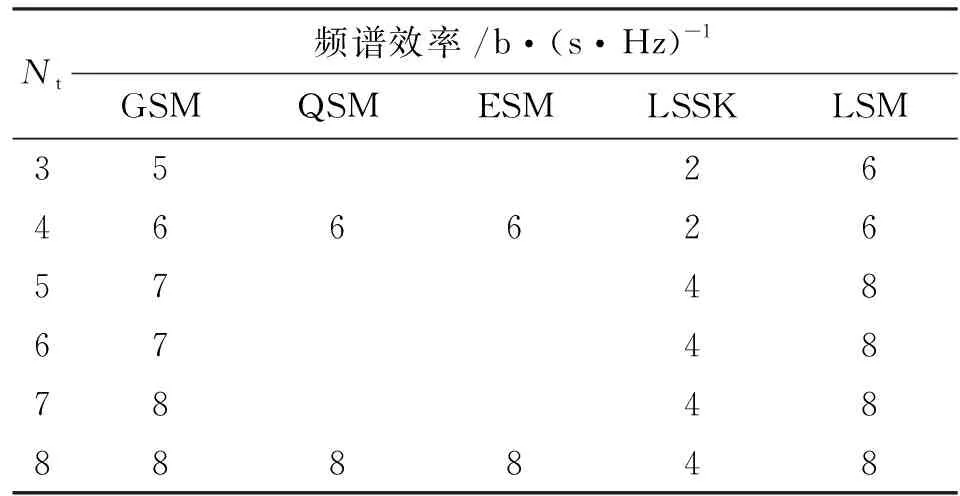
表1 不同發射天線下5種算法的頻譜效率比較
由表1可以發現:相比較于LSSK算法,本文LSM算法通過加入調制符號可以獲得更高的頻譜效率;當發射天線為3、5和6時,LSM算法頻譜效率比GSM高1 b/(s·Hz);相比較于QSM、ESM算法,LSM算法對于任意發射天線數都適應并且可以靈活地調節激活天線的個數。
2.2 LSM比特映射
2.2.1 LSM算法層映射 將待發送比特數據串并轉換得到比特塊g(n)=[b1b2…bj…bLlb(QM)],g(n)含有的比特數是L(lbQ+lbM),其中bj是每個比特塊中的第j個比特,bj等于0或1。然后將比特塊g(n)分成L層平行比特數據塊p(n),p(n)=[b1b2…bi…bL]T,其中bi是第i層,含有(lbQ+lbM)個比特。
2.2.2 LSM算法比特映射 首先確定MIMO系統符號調制階數M和層數L,然后對Nt根發射天線進行編號{1,2,…,Q,…,Nt},其中Q由式(3)確定。
(1)第1層SM映射。將第1層比特數據塊b1分為兩部分,前m1=lbM個比特用來選取幅度為r1的PSK星座點,即調制符號x1,剩余m2=lbQ個比特用來選取激活天線天線索引號a1,即從索引號為{1,2,…,Q}的Q根備選發射天線中選擇激活天線的索引號a1。
(2)第2層SM映射。將第2層比特數據塊b2分為兩部分,前m1個比特用來選取幅度為r2的PSK星座點x2,剩余m2個比特用來選取激活天線的索引號a2。因為第1層已經選擇了索引號為a1的天線,所以第2層選擇激活天線時要排除索引號為a1的天線。同時,為保證第2層備選天線數仍為Q,增加1根索引號為Q+1的天線,即從索引號{1,2,…,a1-1,a1+1,…,Q+1}的Q根備選發射天線中選擇激活天線的索引號a2。
(3)第i層SM映射。將第i層比特數據塊bi分為兩部分,前m1個比特用來選取幅度為ri的PSK星座點xi,剩余m2個比特用來選取激活天線的索引號ai。因為前i-1層已經選取了索引號為{a1,a2,…,ai-1}的天線,所以第i層進行激活天線選擇時要排除{a1,a2,…,ai-1}這些索引號的天線。即從索引號為{1,2,…,Q+i-1}的(Q+i-1)根天線中去掉索引號為{a1,a2,…,ai-1}的i-1根天線后,剩余的Q根天線中再選擇激活天線索引號ai。
(4)依次類推,直到第L層。最后經過L層調制后,就確定了總的天線激活索引號和調制符號。
3 性能分析
本節首先對LSM算法的誤碼性能進行分析,并以系統誤比特率上界為目標函數給出PSK內外環幅度比選擇準則,最后將激活天線索引號和調制符號單獨檢測,提出了一種低復雜度的譯碼算法。
3.1 LSM最優檢測算法誤碼率
這一小節推導LSM系統的誤比特率上界。根據文獻[12],采用最大似然(ML)譯碼時LSM算法的誤比特率可寫為
式中:γ=2L(lbQ+lbM)為所有可能的發送信號總數;Ne,B(sκ→sλ)是信號sκ和信號sλ之間的錯誤比特數;p(sk→sλ)表示發送信號sκ被誤判為信號sλ的概率。根據文獻[12],條件差錯概率為
p(D>0)
(5)
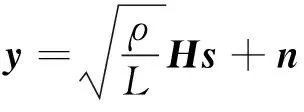
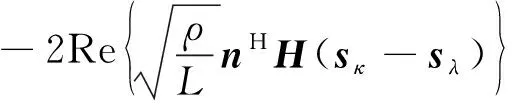
(7)
利用Q(x)≤(1/2)exp(-x2/2),則式(7)中差錯概率上界為
將式(8)代入式(4)可得LSM算法的誤比特率上界為
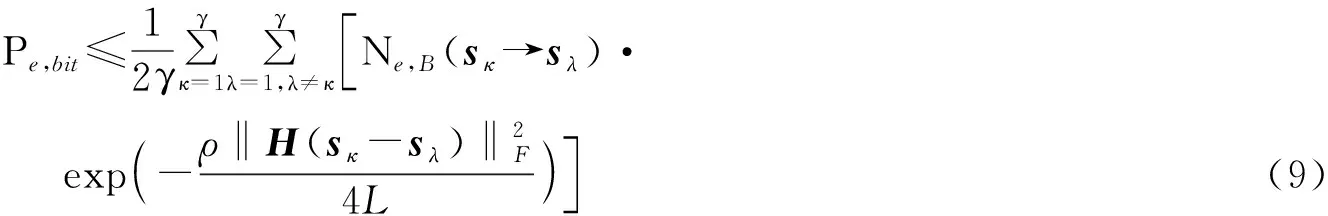
3.2 PSK內外環幅度比算法
如圖1所示,APSK星座的內外環比α=r2/r1,α的取值有無限多個。以誤比特率上界為目標函數通過搜索最小值來確定最優內外環幅度比[13]
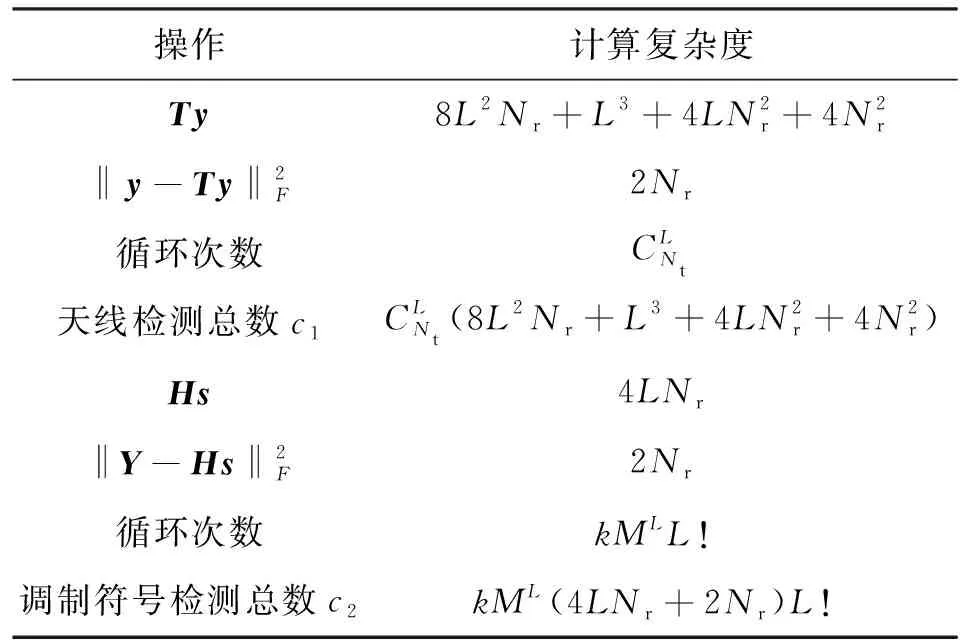
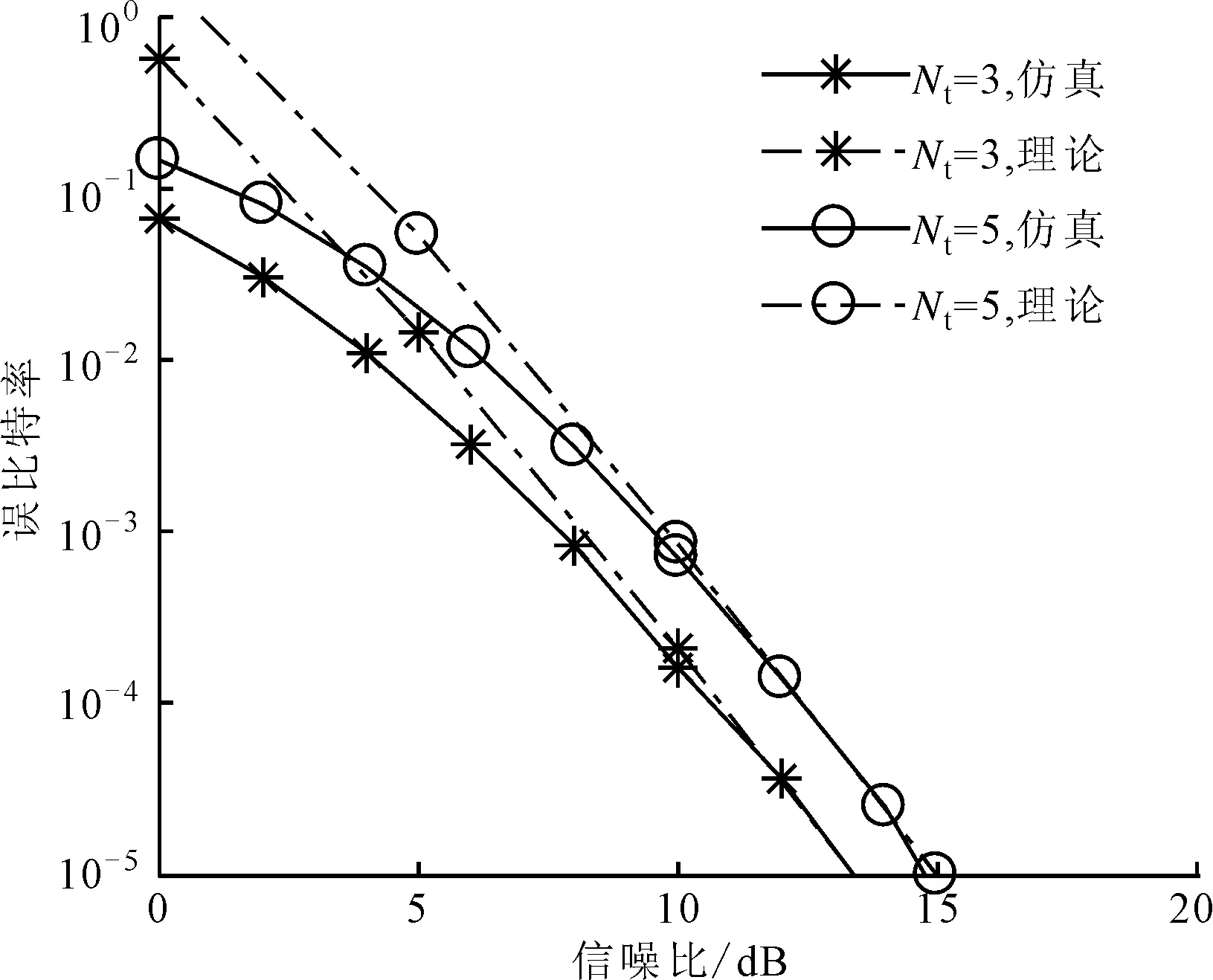
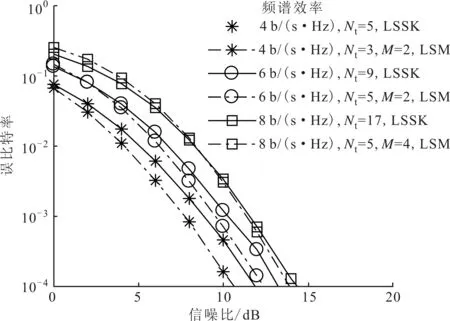
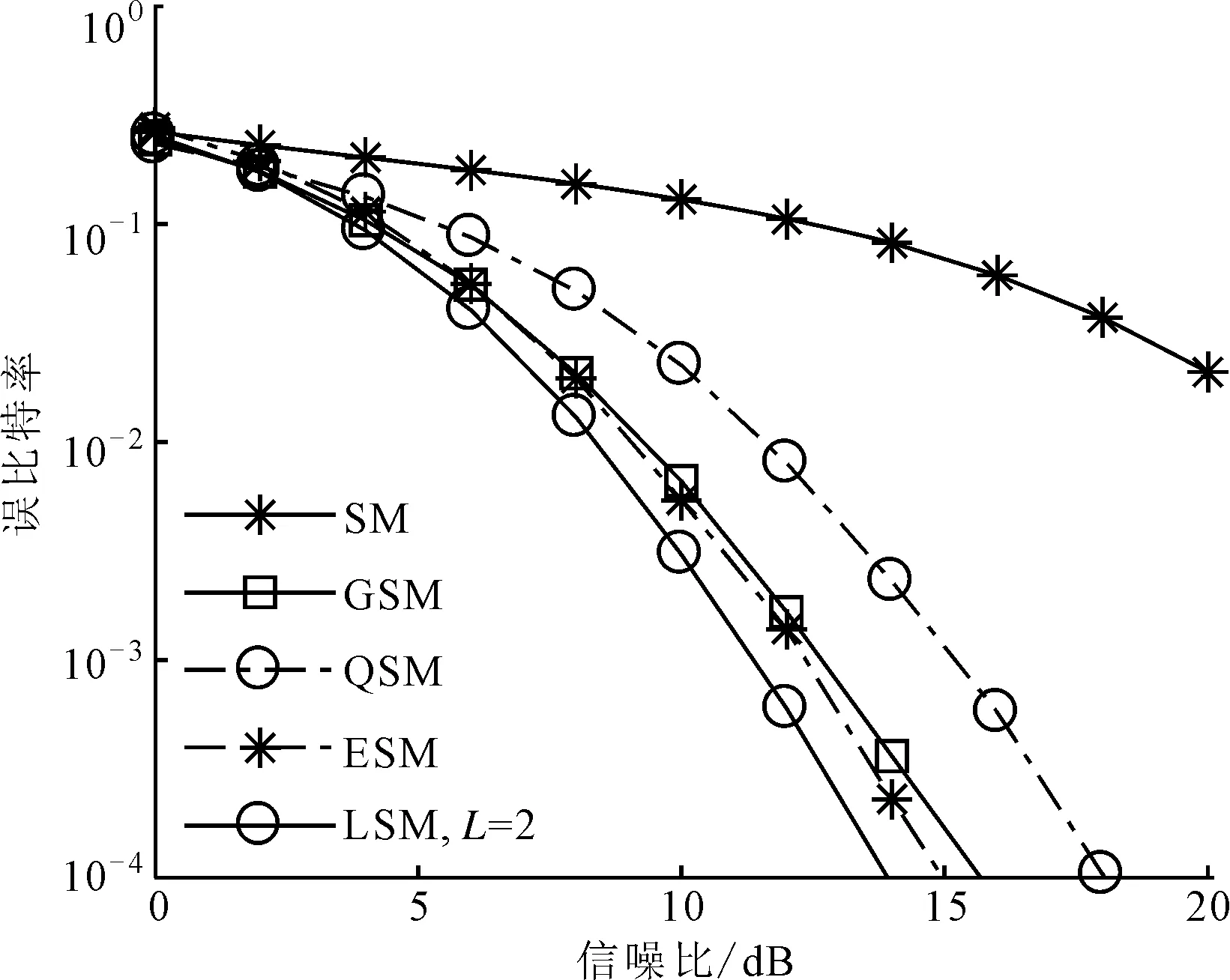
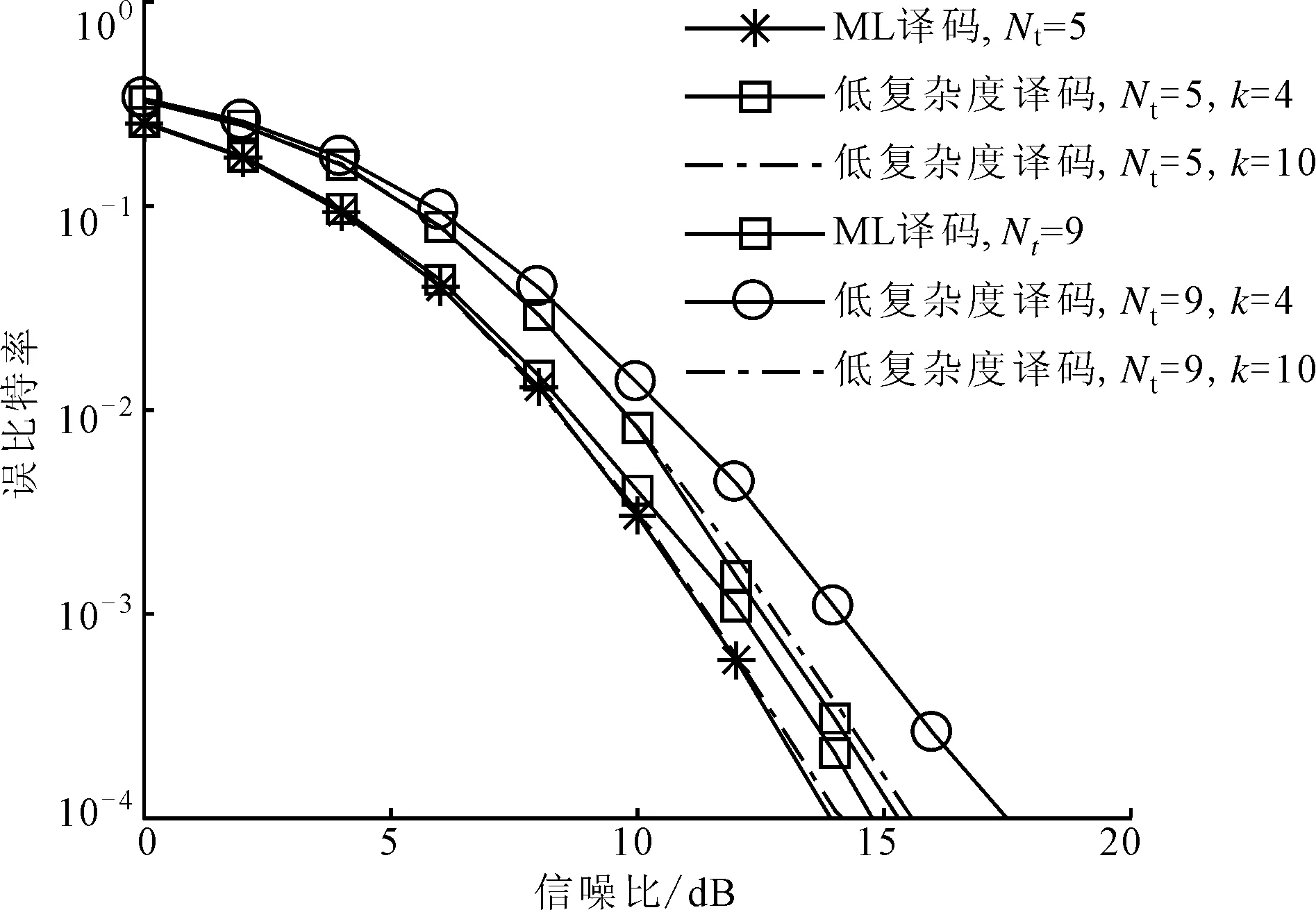
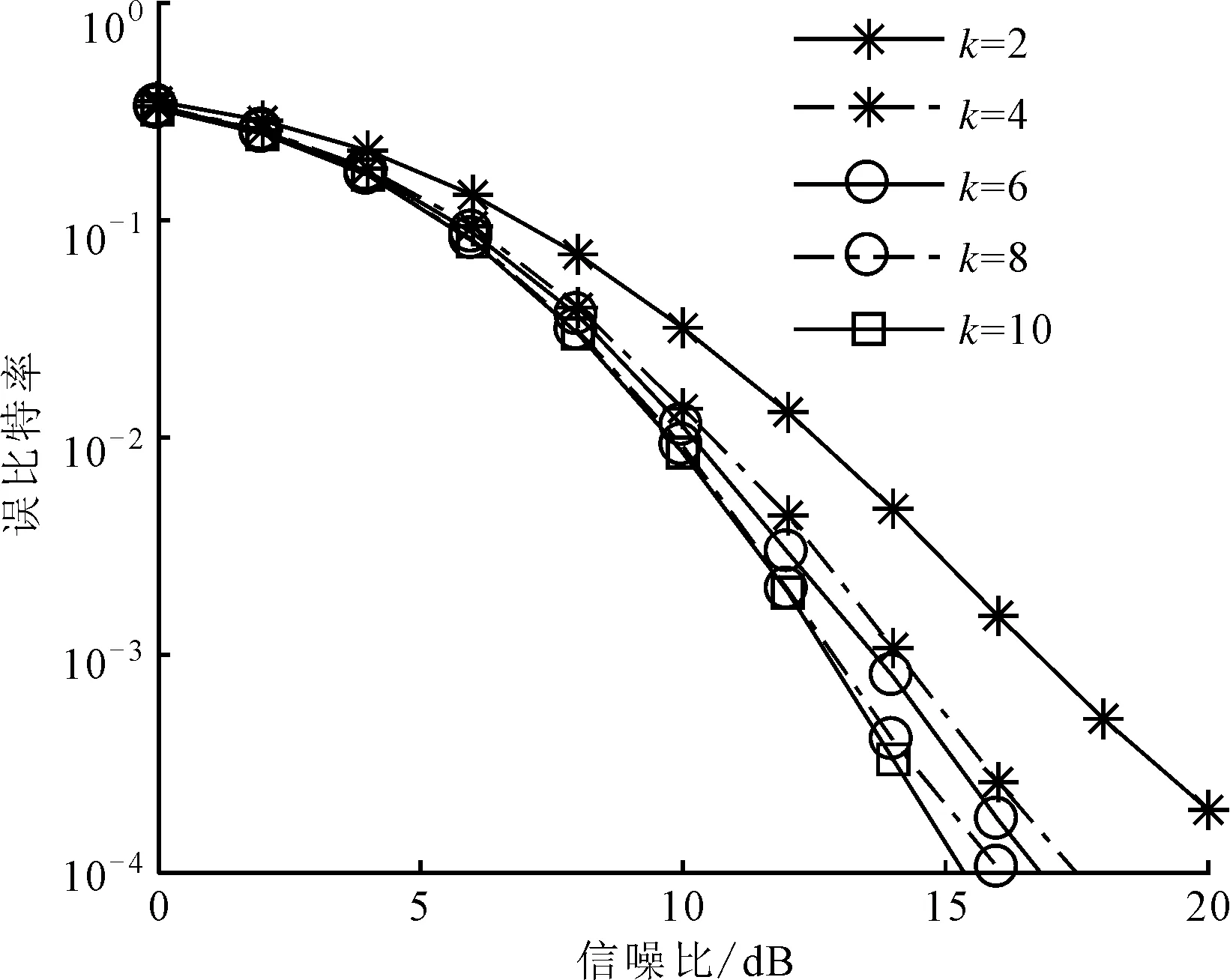
確定MIMO系統的參數Nt、Nr、M、Q、L和一個較高的信噪比(RSN),則α的搜索范圍1<α (1)1<α (2)n*=min{P(n)}即為最優解,此時最優內外環比α*=1+n*Δα。 在上述步驟中,對于一個特定的系統來說,信噪比的取值是可變的。如果信噪比的取值較小,則可能會因為噪聲的原因而得不到理想的內外環幅度比,因此這個算法在信噪比較大時是有效的。同時考慮到在信噪比取到某個較大值時,隨著信噪比的增加,α*是不變的,所以Uupper=3是一個較為合理的值[13]。如果Uupper值設置較小,則可能得不到最優解;如果較大,則會增加搜索的計算復雜度。 圖2給出了在信噪比為15dB、取內外環幅度比α在1~3范圍時,不同系統配置的誤比特率,接收天線個數為4,層數為2。由圖2可知,當Nt=3,M=4時,α*=1.2;當Nt=5,M=4時,α*=1.1;當Nt=5,M=8時,α*=1.6。 圖2 不同系統配置的誤比特率 ML譯碼算法對激活天線的索引號和調制符號聯合譯碼,因此具有較高的復雜度。針對本文算法的特點,提出了一種將天線索引號和調制符號獨立檢測的低復雜度譯碼算法。 根據式(1),Nr×1維接收信號可表示為 式中:hai表示第i層信號經過的Nr×1維的信道向量,同時也是信道矩陣H的第ai列。 式中:dr為升序排序后的第r個值;sort(·)表示排序。 (2)調制符號檢測。為了避免因各個信道向量不正交而使得系統性能較差的問題,本文選取式(12)中前k個值來進行激活天線檢測和調制符號的聯合檢測,1≤k≤K。k的值決定了系統性能和復雜度之間的權衡。由式(12)中前k個較小的值,得到相應的k個子空間侯選集,則第i個子空間侯選集Ri可表示如下 式中:hi為信道矩陣H的第i列,i=1,2,…,L。 因為每個信道傳送的調制符號來自不同幅度的星座點,所以根據調制符號就可以判斷信道選擇次序。在侯選集中做最大似然檢測算法來確定調制符號,公式如下 表2和表3分別給出了ML譯碼算法和本文提出的低復雜度譯碼算法的每一步的計算次數及計算復雜度,其中計算復雜度由運算過程中所需的浮點數來衡量。 表2 ML算法的計算復雜度 表3 低復雜度譯碼算法的計算復雜度 以Nt=129、Q=128、L=2、Nr=4、M=16的系統為例[11],當k=4時,ML檢測的計算復雜度是167772160,本文低復雜度譯碼算法檢測的計算復雜度是2789888,只有ML檢測算法的1.66%,因此在發射天線數較多及參數k較小時,本文低復雜度譯碼算法可以有效降低計算的復雜度。 為了驗證所提算法的有效性,本節對SM、LSSK、GSM、QSM、ESM和LSM算法的誤比特率性能進行了仿真,并對仿真結果進行了比較。仿真均假定各天線之間的信道是相互獨立的,并且服從CN(0,1)分布,不同方案的接收天線均設為4。 圖3給出了Nt=3、Q=2、L=2、M=4和Nt=5、Q=4、L=2,M=4時,本文LSM的理論上界與蒙特卡洛方法仿真結果比較。由圖3可以看出,在高信噪比的情況下理論分析結果能夠很好地吻合仿真結果,從而證明了理論分析的正確性。 圖3 本文LSM算法的理論和仿真比較 圖4 LSSK與LSM性能比較 圖4給出了當層數L=2時,LSSK和LSM算法的誤比特率仿真曲線。由圖4可以看出,當頻譜效率為4b/(s·Hz)和6b/(s·Hz)時,LSM算法的發射天線個數不僅比LSSK算法少,性能也優于LSSK算法。其主要原因是由于LSM算法加入了符號調制,使得LSM算法有更高的頻譜效率,同時當頻譜效率為8b/(s·Hz)時,LSM和LSSK算法的性能基本一致,但是LSM比LSSK算法節省了12根發射天線,從而節約了硬件資源。 圖5給出了本文LSM算法與SM、GSM、QSM、ESM算法在相同的天線配置與頻譜效率下,采用最大似然檢測的仿真結果。由圖5可以看出,LSM算法的性能明顯優于其他算法。這是因為LSM采用APSK信號不僅能夠區分各層而且還能夠獲得較大的歐式距離,從而更好地利用空域傳輸信息。 圖5 本文LSM算法與其他4種算法的性能比較 圖6給出了ML和本文低復雜度譯碼算法的性能比較。其中,低復雜譯碼算法的參數k分別為4和10。由圖6可知,低復雜度譯碼算法表現出近最大似然算法的性能,并且隨著低復雜度譯碼算法的k值的增加,低復雜度譯碼算法與ML性能基本一致。其主要原因是誤差個數k增加時需要更多的候選子空間,當k等于總的子空間個數K時也就等價于ML檢測。 圖6 本文低復雜度譯碼算法與ML譯碼算法的性能比較 圖7給出了本文低復雜度譯碼算法取不同k值時誤比特率仿真比較。由圖6和圖7可知,在低信噪比情況下,低復雜度譯碼能夠在獲得接近ML檢測性能的同時有效地降低了檢測復雜度。在高信噪比時,低復雜度譯碼算法通過增加k值仍能獲得接近ML檢測的性能。 圖7 不同k值下低復雜度譯碼算法的性能比較(Nt=9) 針對空間調制頻譜效率較低的問題,本文提出了一種基于幅度/相移鍵控的分層SM算法——LSM算法通過。該算法加入分層結構來發射多層SM信息,有效地提高了系統的頻譜效率。同時,以系統誤比特率上界為目標函數,提出了一種優化算法來確定APSK內外環幅度比。最后,將激活天線索引號和調制符號單獨檢測,提出了一種低復雜度譯碼算法。理論分析和仿真結果表明,在相同頻譜效率下,本文LSM算法的性能優于現有的GSM、QSM、ESM等算法。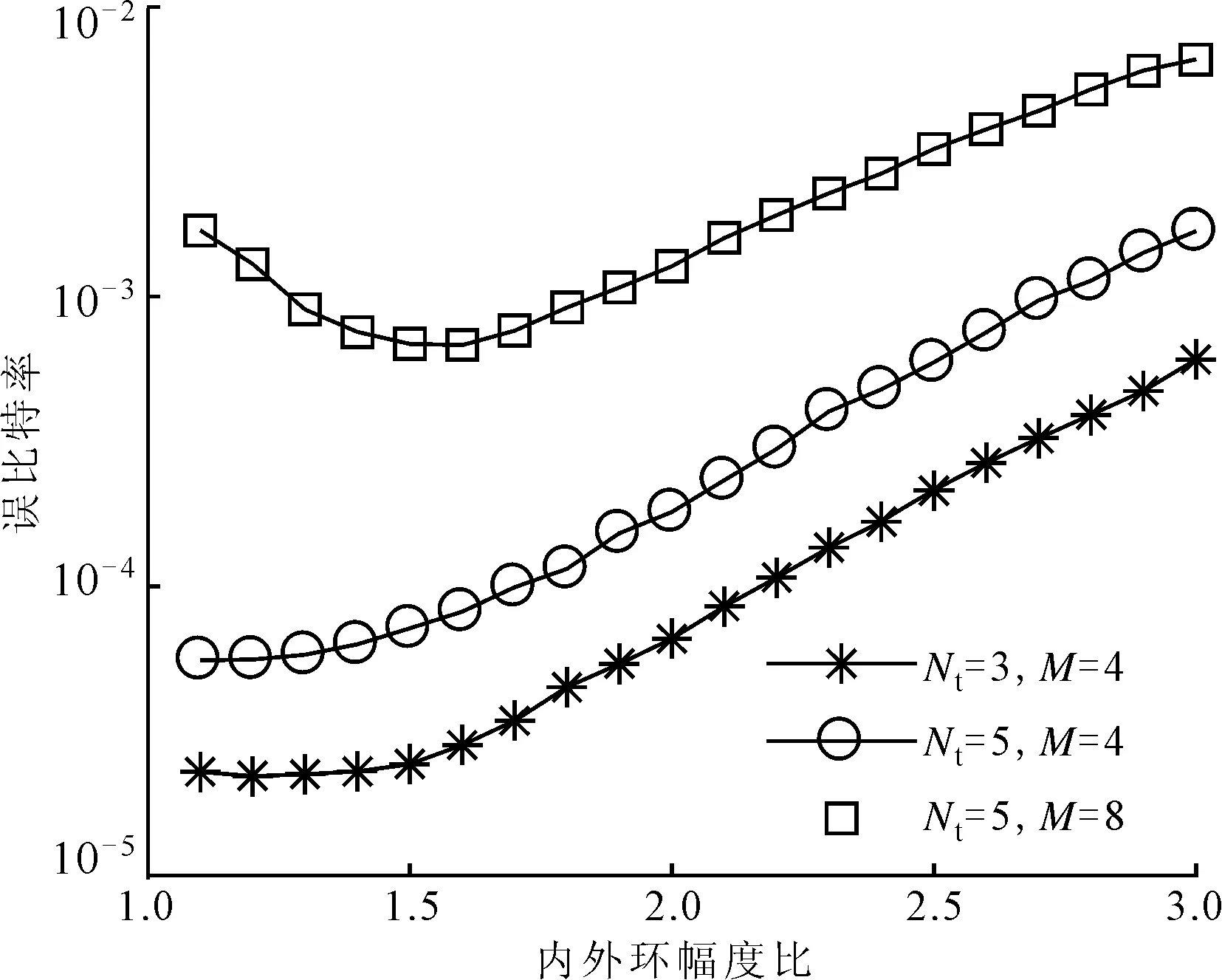
3.3 接收端低復雜度譯碼算法
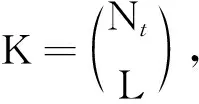

4 仿真結果與討論
5 結束語

